气泡在化工、生物、医药、动力设备、核反应堆、航天和热能等多个领域有着广泛的应用,譬如:大型船舶的气泡减阻、油气输运、血管中气泡的运动。船舶发动机水下排气会造成螺旋桨的气蚀, 利用气泡可以加速反应装置中的物质混合、热量交换及化学反应过程;在水处理方面,曝气、气浮等工艺的处理能耗和处理效率与气泡运动特性密切相关。在沸腾传热中,气泡脱离是沸腾传热的重要过程,气泡从基板上脱离受多个因素的影响,包括气泡的形状、大小、加热模式、基板表面的润湿性等。
Fritz和Ende[1]通过气泡脱离时的受力分析,得到著名的Fritz公式,在常压情况下,该公式的计算结果与实验结果较为吻合,但当压力过高或过低时有误差。Cole[2]在低压条件下进行一系列的气泡生长和脱离的实验,并得到新的拟合关系式,该式中引入一个Jakob数,后来得到广泛引用。Rohsenow[3]发现气泡生长需要的一定过热度,其大小由气液界面的表面张力决定。Lee和Nydahl[4]对气泡的生长和脱离进行数值模拟,假设气泡具有球缺形状并且在整个气泡生长期间存在微层, 他们发现,微层蒸发的热量占整个核态沸腾换热量的87%。Zeng等[5]提出,气泡在上升与分离时主要由气泡受到的浮力以及表面张力决定,据此获得气泡生长和气泡分离直径的表达式。Son等[6]使用Level Set方法对水沸腾期间气泡的生长和离开进行数值模拟。Fuchs等[7]利用数值模拟的方法,分析壁面导热效应和蒸发弯月面对气泡生长和脱离的影响。本文利用数值模拟的方法,对于气泡脱离基板的机理进行深入全面的研究。
1 模型和公式本文利用Level Set方法建立二维轴对称非稳态数学模型,用有限差分法对控制方程进行离散处理,在给定的边界条件下,追踪气液界面的演化规律,获得气泡在浮力、黏性力、惯性力与表面张力共同作用下的运动规律,分析不同接触角、Re数和Bo数对气泡脱离基板的影响,并获得气泡从基板脱离时的临界参数。
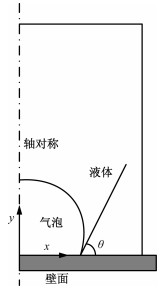
本文中,以单个气泡为研究对象,气泡初始形状为球缺形。由于气泡沿y轴方向是轴对称的,我们仅对气泡x轴正方向的部分进行模拟,计算区域底部为无滑移边界条件,其余边界为自由边界条件,如图 1所示。数值模拟结果表明,当气液的密度比和黏性比小于0.05时,该比值对于气泡的运动规律几乎没有影响,因此选取气液的密度比和黏性比为0.05。气泡无初始速度,在脱离基板的过程中满足质量守恒。经过校验后,网格数101×301,时间步长为1.0×10-4,计算域为3×9。
|
Download:
|
| 图 1 气泡脱离基板示意图 Fig. 1 Schematic of bubble detachment from substrate | |
由于气泡是在浮升力的驱动下脱离的,因此以浮升力来定义特征速度
| $U=\sqrt{g R}, $ | (1) |
引入无量纲参数:
| $R e=\rho_{1} U R / \mu_{1}, $ | (2) |
| $B o=\rho_{1} g R^{2} / \sigma. $ | (3) |
分析得到气泡脱离壁面的无量纲控制方程如下:
连续性方程:
| $\nabla \cdot \boldsymbol{u}=0, $ | (4) |
动量方程:
| $\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u} \cdot \nabla \boldsymbol{u}=-\frac{1}{\rho} \nabla p+\frac{1}{\rho^{*} R e} \nabla \cdot\left[\mu^{*}\left(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{\mathrm{T}}\right)\right]+\\ \frac{1}{\rho^{*} B o} \kappa \boldsymbol{n} \delta(\phi)+\frac{1}{\rho^{*}}\left(1-r_{\mathrm{d}}\right) j. $ | (5) |
式中:ρ*=ρg/ρl,μ*=μg/μl分别为气泡内外的密度比和黏度比。
2 结果与讨论气泡脱离基板的过程受众多因素的影响,将控制方程进行无量纲化以后,这些因素可以归结为Re数、Bo数和接触角的影响。
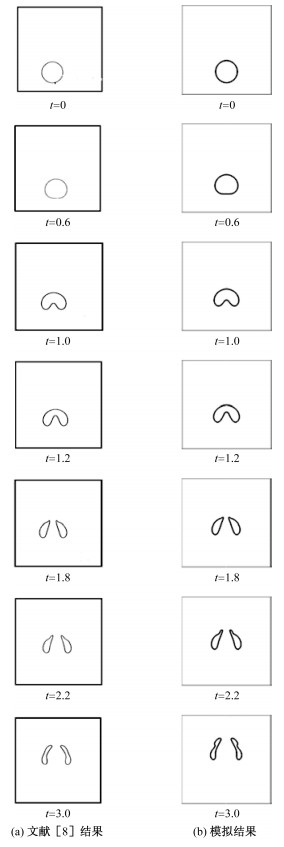
2.1 模型校核为了验证模型的正确性,我们与Sussman和Smereka[8]的结果进行比较,如图 2所示。结果表明,我们的模拟结果和他们的结果非常符合。气泡在浮力作用下,由静止开始上升,圆形气泡下部开始变形,进而导致气泡破裂。
|
Download:
|
| 图 2 Re=100和Bo=2时气泡运动过程的形状演化 Fig. 2 Bubble shape evolution at Re=100 and Bo=2 | |
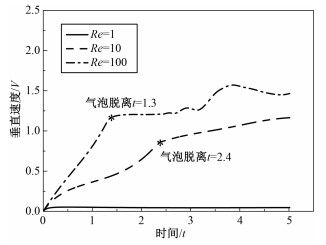
首先通过改变气泡脱离基板时的Re数(其中Bo=1,θ=60°),研究Re数的变化对气泡脱离基板的影响。由图 3可知,不同Re数下气泡脱离基板的垂直速度明显不同,当Re=1时,由于黏性的影响,气泡无法脱离,气泡的垂直速度很小,可忽略不计;当Re=10时,气泡脱离基板的垂直速度随时间增长而增加,t=2.4时开始脱离基板,;当Re=100时,气泡脱离明显提前,t=1.3时气泡就能够开始脱离,气泡脱离基板的垂直速度也随时间增长而增加,且相比Re=10时,气泡脱离基板的垂直速度较大。
|
Download:
|
| 图 3 不同Re数下气泡脱离基板的垂直速度变化规律(Bo=1,θ=60°) Fig. 3 Variations in vertical velocities of bubble detachment from substrate at different Reynolds numbers at Bo=1 and θ=60° | |
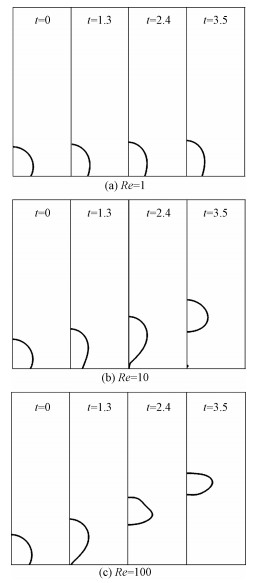
图 4是不同Re数下气泡形状随时间的变化(Bo=1,θ=60°)。当Re=1时,气泡虽然不能脱离,但是由于浮力的作用,气泡形状略有变化,在竖直方向上被拉伸;当Re=10时,气泡能够沿竖直方向脱离,气泡先是在竖直方向上被拉伸,然后在t=2.4时刻气泡开始脱离,气泡在上升过程中基本为半球形,形状变化不剧烈;当Re=100时,气泡在t=1.3时刻就开始脱离基板,且气泡在上升过程中形状变化较为剧烈,脱离之后气泡变得更加扁平。总体来说,当Bo数和接触角不变时,Re数越大,气泡越容易脱离,气泡脱离基板的垂直速度越大,形状变化越剧烈。
|
Download:
|
| 图 4 不同Re数下气泡形状的变化(Bo=1,θ=60°) Fig. 4 Evolution of bubble shapes at different Reynolds numbers at Bo=1 and θ=60° | |
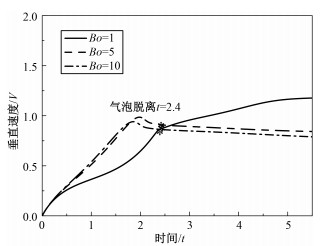
图 5为不同Bo数下气泡脱离基板的垂直速度的变化规律(Re=10,θ=60°)。可以看出,在气泡脱离基板前,气泡的垂直速度随着时间推移而增加,但是Bo=1时的垂直速度较小;在Bo=5或Bo=10时,垂直速度随着时间几乎是线性的增加。而在气泡脱离基板后,Bo=1时,气泡速度持续增加,而Bo=5或Bo=10时,气泡速度达到稳定值。总体来说,当Re数和接触角不变时,Bo数越大,气泡脱离基板的垂直速度越大,但是Bo数到达一定程度时,其对气泡的影响会很小。
|
Download:
|
| 图 5 不同Bo数下气泡脱离基板的垂直速度变化规律(Re=10,θ=60°) Fig. 5 Variations in vertical velocities of bubble detachment from substrate at different Bond numbers at Re=10 and θ=60° | |
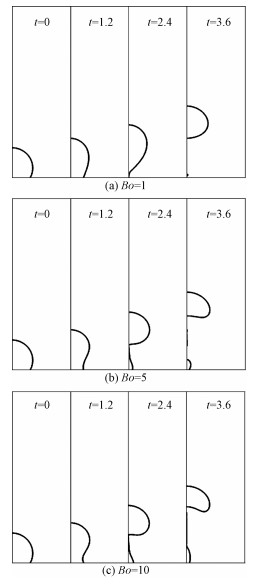
图 6为不同Bo数下时气泡脱离基板过程中的形状变化(Re=10,θ=60°)。可以看出,在不同的Bo数下,气泡均能够从基板脱离,且脱离的时间都在t=2.4左右。在气泡脱离基板之前,气泡在浮力的作用下被逐渐拉伸,在Bo=1时,气泡能够完全脱离基板,而在Bo=5和Bo=10时,由于气泡表面张力比Bo=1时要低,在气泡周围液体惯性力的作用下,气泡的底部会断裂,从而使小部分气体附着在基板上,而其余部分脱离基板,这也是图 4中Bo=5和10的时候,气泡的垂直速度与Bo=1时不同的原因。
|
Download:
|
| 图 6 不同Bo数下气泡形状的变化(Re=10,θ=60°) Fig. 6 Evolution of bubble shapes at different Bond numbers at Re=10 and θ=60° | |
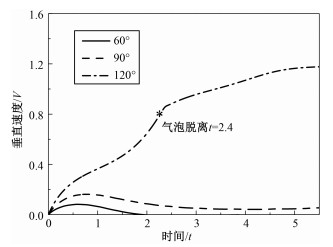
图 7为不同接触角下气泡脱离基板的垂直速度变化曲线(Re=10, Bo=1)。可以看出,接触角的大小对气泡脱离基板有很大的影响。当接触角θ=120°时,气泡无法成功脱离基板;当θ=90°时,气泡能够脱离基板,但是需要较长的时间,在t=9.7才能开始脱离,刚开始气泡脱离基板的垂直速度的增长较为缓慢;而当θ=60°时,气泡脱离基板的垂直速度随时间的增长迅速增大,在t=2.4时就开始脱离基板。
|
Download:
|
| 图 7 不同接触角下气泡脱离基板的垂直速度变化规律(Re=10,Bo=1) Fig. 7 Variations in vertical velocities of bubble detachment from substrate at different contact angles at Re=10 and Bo=1 | |
图 8为不同接触角下气泡形状的变化规律(Re=10,Bo=1)。可以看出,接触角θ=120°时,气泡无法成功脱离,气泡形状也基本没有变化,竖直方向并没有明显地被拉伸;接触角θ=90°时,气泡在脱离基板的过程中由于浮力的作用逐渐被拉伸,而后逐渐脱离基板;接触角θ=60°时,由于气泡与基板接触面积的减小,气泡更容易脱离。

|
Download:
|
| 图 8 不同接触角下气泡形状的变化(Re=10,Bo=1) Fig. 8 Evolution of bubble shapes at different contact angles at Re=10 and Bo=1 | |
本文利用Level Set方法,针对气泡脱离基板的运动建立瞬态二维轴对称模型,分别研究Re数、Bo数和接触角的大小对气泡脱离基板规律的影响,所得结论如下:
1) 随着Re数的增大,气泡所受的惯性力越大,气泡越容易脱离基板,即气泡脱离基板的垂直速度增长越快,开始脱离的时间越早。
2) 随着Bo数的增大,在气泡脱离之前,气泡的垂直速度增加得越快,但是对于气泡脱离的时间影响不大。Bo数增大时,气泡从完全脱离变成部分脱离。
3) 气泡与基板的接触角越大,与基板的接触面积越大,与基板底部和附近液体的作用力就越大,因而越难以脱离。这也进而说明基板的润湿性对于气泡脱离有很大的影响。
| [1] |
Fritz W, Ende W. Berechnungdes maximal volumens von dampfslasen[J]. Physik Zeitschr, 1935, 36: 379-384. |
| [2] |
Cole R. Bubble frequencies and departure volumes at subatmospheric pressures[J]. AIChE Journal, 1967, 13: 779-783. Doi:10.1002/aic.690130434 |
| [3] |
Rohsenow W M. A method of correlating heat transfer data for surface boiling of liquids[J]. Transaction of American Society of Mechanical Engineers, 1952, 74: 969-976. |
| [4] |
Lee R C, Nydahl J E. Numerical calculations of bubble growth in nucleate boiling from inception through departure[J]. Journal of Heat Transfer, 1989, 111: 474-479. Doi:10.1115/1.3250701 |
| [5] |
Zeng L Z, Klausner J F, Mei R. A unified model for the prediction of bubble detachment diameters in boiling system1-1.pool boiling[J]. International Journal of Heat and Mass Transfer, 1993, 36: 2261-2270. Doi:10.1016/S0017-9310(05)80111-5 |
| [6] |
Son G, Dhir V K, Ramanujapu N. Dynamics and heat transfer associated with a single bubble during nucleate boiling on a horizontal surface[J]. Journal of Heat Transfer, 1999, 121: 623-631. Doi:10.1115/1.2826025 |
| [7] |
Fuchs T, Kern J, Stephan P. A transient nucleate boiling model including microscale effects and wall heat transfer[J]. Journal of Heat Transfer, 2006, 128: 1257-1265. Doi:10.1115/1.2349502 |
| [8] |
Sussman M, Smereka P. Axisymmetric free boundary problems[J]. Journal of Fluid Mechanics, 1997, 341: 269-294. Doi:10.1017/S0022112097005570 |
 2020, Vol. 37
2020, Vol. 37 


