液滴撞击液膜现象广泛存在于喷雾冷却、降膜蒸发、喷墨打印[1-4]等诸多工业应用。与液滴直接撞击固体壁面相比,液滴撞击液膜展现完全不同的动态行为与动力学特征,例如出现液滴与液膜的融合、反弹、飞溅水花等现象。对于这样一个复杂的动态变化过程,其影响因素众多,除液滴自身性质如液滴大小、撞击速度、黏度、密度等因素外,还与液膜物性和固体表面结构、粗糙度、浸润性等有关,其中固体表面结构对液滴撞击液膜后的动态形变具有显著影响。
目前对于液滴撞击液膜现象的研究主要有理论分析、实验研究和数值分析3个方面。Wang和Chen[5]对单液滴撞击平板极薄液膜的现象进行实验研究,发现液膜无量纲厚度小于0.1时,液膜厚度不影响飞溅发生时的临界We数。Wal等[6]研究液滴撞击后的飞溅现象,给出飞溅的定义,即有小液滴从水花边缘分离的现象,归纳了发生飞溅时的临界参数。Chen等[7]通过实验手段系统地研究液滴撞击互溶和不互溶的液膜现象,结果表明,对于与液滴互溶的液膜,需要更大的We数和更厚的液膜厚度才能形成冠状水花和飞溅现象。Dai等[8]采用CLSVOF(couple level-set and volume of fluid)方法模拟单液滴撞击倾斜液膜的演变和飞溅过程。Shetabivash等[9]采用VOF方法和自适应网格技术模拟液滴撞击薄液膜过程,研究气体密度、黏度和液膜厚度对冠状水花半径和高度的影响。王小永等[10]采用LBM方法分析二维液滴撞击液膜的过程,并且考察液膜流动作用对水花铺展半径和溅起高度的影响。郭亚丽等[11]采用CLSVOF方法模拟双液滴同时撞击液膜的流动过程,We数较大时中心射流顶端将产生二次液滴。Liang等[12-13]对液滴撞击倾斜润湿壁面进行实验观测,定性给出反弹和局部反弹的条件:较高的流体黏度、较小的撞击角和We数; 还开展液滴撞击弯曲润湿壁面过程的实验及数值模拟研究,发现润湿圆柱的弯曲效应会导致等压面在撞击后期向母线方向收缩。Hao等[14]研究液滴撞击附着在微柱结构表面的液膜的过程,发现微柱间隙可以抑制液滴在表面液膜上的反弹。
到目前为止,虽然针对液滴撞击液膜的动态行为已经开展了大量研究工作,但是多集中于液膜物性、液膜厚度、撞击速度和壁面曲率的影响,而忽略了固体表面微小结构与表面液膜之间的相互作用关系,由于表面槽道的毛细作用使得液滴撞击液膜后的行为演化与液滴撞击光滑表面有了显著的差异。此外,固体表面上特殊的微观结构在自然现象和工程领域中均体现出重要作用,例如表面自清洁、防水、防结冰[15-16]等应用。超疏水表面[13]的微观结构有利于液滴撞击壁面的反弹,从而抑制结冰,Guo等[17]的研究也发现疏水沟槽的表面有助于液滴的迅速脱离。而上述的这些过程都不能忽视液滴与具有表面微观结构上的液膜之间发生的碰撞及相互作用,它们之间的相互作用机制尚未明晰。由此可见,壁面结构对撞击后表面液膜和液滴的行为有着显著影响。因此,本文采用数值模拟方法,对不同壁面结构时液滴撞击液膜的动力学特性的变化规律进行探讨,从而为喷雾冷却、表面自清洁、防结冰等工业领域研究提供理论基础。
1 数学模型 1.1 CLSVOF模型介绍VOF方法通过定义体积分数α追踪界面,体积分数定义为单元中流体体积与单元体积之比,单元中充满液体为α=1,充满气体α=0,相界面为0 < α < 1。α的控制方程为
| $\frac{\partial \alpha}{\partial t}+\boldsymbol{U} \cdot \nabla \alpha=0, $ | (1) |
式中:U为速度,t为时间。
Level-set方法则是定义相界面的有符号距离函数,相界面为隐式函数的零等值面,可以表示为φ(x, t)=0。在两相流系统中:
| $\varphi (x, t) = \left\{ {\begin{array}{*{20}{c}} { + |d|}&{{\rm{连续相}}}\\ 0&{{\rm{ 相界面}}}\\ { - |d|}&{{\rm{ 离散相}}} \end{array}} \right., $ | (2) |
式中:d是相界面距离。φ的控制方程为
| $\frac{\partial \varphi}{\partial t}+\boldsymbol{U} \cdot \nabla_{\varphi}=0. $ | (3) |
VOF函数能很好地保证物理量的守恒,但是无法精确估算界面的法向量、曲率。LS函数是一个距离函数,可以精确计算界面曲率,但是质量不守恒。在CLSVOF方法中,同时使用VOF函数和LS函数,通过耦合两种函数,使得CLSVOF同时具有以上二者的优点。因此本文采用CLSVOF方法对液滴撞击凹凸槽道液膜进行数值模拟。在CLSVOF方法中,将两相流的控制方程写成统一形式。
对于不可压缩流体,其连续性方程和动量方程如下所示:
| $\nabla \cdot \boldsymbol{U}=0, $ | (4) |
| $\begin{array}{l} \frac{{\rho \partial \mathit{\boldsymbol{U}}}}{{\partial {\rm{t}}}} + \rho \nabla \cdot (\mathit{\boldsymbol{UU}}) = - \nabla \cdot p + \\ \;\;\;\;\;\;\;\;\nabla \cdot \mu \left[ {\nabla \mathit{\boldsymbol{U}} + {{(\nabla \mathit{\boldsymbol{U}})}^{\rm{T}}}} \right] - \sigma \kappa \delta (\varphi )\nabla \varphi + \rho \mathit{\boldsymbol{g}}. \end{array} $ | (5) |
式中:κ是界面曲率,通过下列公式得到:
| $\kappa=\nabla \cdot \frac{\nabla_{\varphi}}{\left|\nabla_{\varphi}\right|}, $ | (6) |
| $\delta (\varphi ) = \left\{ {\begin{array}{*{20}{c}} {\frac{{1 + \cos \pi \varphi /a}}{{2a}}}&{|\varphi | < a}\\ 0&{|\varphi | > a} \end{array}} \right. . $ | (7) |
式中:a=1.5 s,s是最小网格尺寸。界面法向量n计算如下
| $\boldsymbol{n}=\frac{\nabla_{\varphi}}{\left|\nabla_{\varphi}\right|}. $ | (8) |
在追踪移动相界面时,由于数值耗散导致界面轮廓总是变得模糊以及震荡,因此有必要在每一次时间步迭代后进行界面重构,在CLSVOF方法中,采用分段线性的几何重构思想,将单个网格内的界面用线段代替,同时利用Level-set方法求出界面的法向量以确定界面方向,结合VOF方法求解出的网格内的体积分数,重构出网格界面。
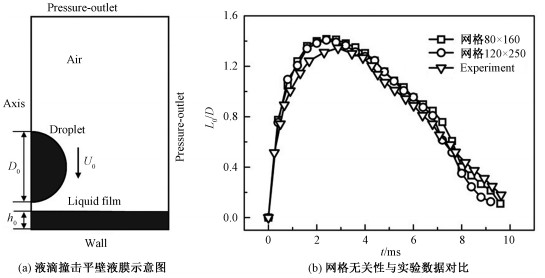
1.2 模型验证通过两个case的模拟与实验现象的对比,以验证模型的准确性。case1先模拟水滴撞击平壁油膜,两者工质不相融,初始时刻模型如图 1(a)所示,计算区域为高6 mm,宽3 mm的二维矩形区域,采用均匀四边形网格,液膜区域网格局部加密,计算工质为空气、液滴为水,液膜为krytox103号润滑油,液滴直径2 mm,液滴撞击速度为0.6 m/s(We=10),油膜厚度为50 μm,油膜黏度0.15 Pa·s,液滴中心下落高度为1.1 mm。底部为无滑移边界条件,顶部和右侧为Pressure-outlet,左侧为轴对称边界条件。采取不同的网格尺寸进行试算,计算结果如图 1(b)所示。图 1(b)为不同网格尺寸下液滴最大铺展因子L0/D随时间的变化过程,并且与实验数据[14]对比,铺展因子与实验数据非常吻合。当网格尺寸小于液滴直径的1/50[13]时,网格数量对模拟结果影响较小,且足以精确地捕捉相界面。
|
Download:
|
| 图 1 模型验证 Fig. 1 Model validation | |
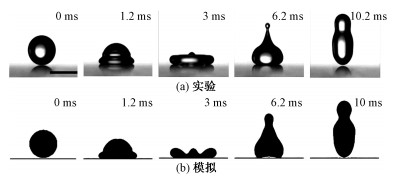
图 2为液滴形态变化与实验对比图,可以看出文献中实验得出的液滴形态变化和模拟得出的基本一致。
|
Download:
|
| 图 2 水滴撞击油膜形态变化图 Fig. 2 Evolution of a water droplet impact on oil surface | |
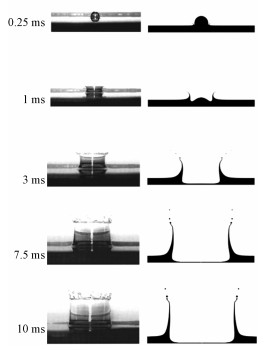
case2模拟液滴撞击同种工质,液滴与液膜都是70%甘油与水的混合溶液,液滴直径2.5 mm,工质密度1 200 kg/m3, 液滴撞击速度为5.1 m/s(We=2 010),液膜厚度为2.5 mm,液膜黏度0.022 Pa·s。底部为无滑移边界条件,顶部和右侧为Pressure-outlet,模拟结果与实验[5]对比如图 3所示。液滴与液膜融合后,在液滴与液膜接触的地方出现颈部射流,随着时间推移,射流的高度和直径不断增加,冠状水花顶部在Rayleigh-Plateau不稳定性的作用下,出现二次液滴。模拟结果表明可以精确捕捉实验现象中的二次液滴的生成,再一次证明该模型的准确性。本文采用40 μm的网格尺寸,但在液膜局部网格尺寸进行加密,最小网格尺寸为5 μm。对流离散格式采用QUICK格式,压力-速度耦合求解采用PISO算法,对Level Set方程的求解采用QUICK算法。
|
Download:
|
| 图 3 液滴撞击相同工质形态变化与实验对比图 Fig. 3 Morphology change of droplet impact into the same material and comparison with experiment | |
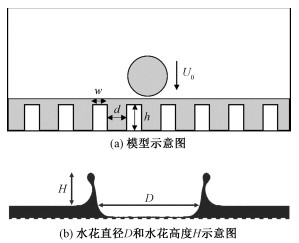
本文进行液滴撞击不同宽高比凹凸槽与平壁的形态对比研究,建立液滴撞击液膜(液滴与液膜均采用70%甘油与水混合溶液)二维模型,如图 4(a)所示。长20 mm,高10 mm,液滴直径2 mm,液膜厚度1 mm,w代表槽道宽度,h代表槽道高度,d代表槽道间距,液滴撞击速度3.43 m/s,密度1 200 kg/m3,黏度0.022 Pa·s,表面张力0.0 652 N/m。采用之前验证的网格尺寸,网格数量为6万,液膜附近进行网格加密。图 4(b)为水花直径D和水花高度H示意图。
|
Download:
|
| 图 4 液滴撞击槽道结构表面液膜 Fig. 4 Schematic of droplet impact into rectangular grooved surface with liquid film | |
图 5为直径2 mm的液滴撞击槽道高度分别为0.1、0.3、0.5 mm的液膜后的流动演变图,分别对应图 5(a)、5(b)、5(c),槽道宽0.3 mm,间距0.3 mm。从图 5(a)可以看出,液滴撞击液膜后,在液滴与液膜接触的颈部区域产生向外扩展的射流,如图 0.8 ms所示。随着液滴与液膜的融合,周围流体不断进入到射流中形成冠状水花(2.8 ms),其水花高度和水花直径不断增大,即液滴的动能转变为水花向上发展和向两侧扩展的动能。当水花高度达到最大,在重力的作用下,水花高度下降,然而受水平方向惯性力的影响,水花直径仍然在向外扩张,推动液膜向外流动。对比0.1、0.3、0.5 mm高度下的流动过程,虽然三者碰撞过程中都有冠状水花出现,但是只有高0.5 mm槽道的液膜产生卫星液滴。整个撞击过程中,随着凹凸槽高度的增大,槽道顶端到液膜表面的距离减少,撞击过程中表层液膜将获得更多的动能,使得水花形态变化更加明显,且在更短时间内消失。从2.8 ms及其之后的时间推移图像可以看出,随着表面上微槽高度h的增加,撞击后液膜向外倾斜更加明显,而下半部的角度也呈现明显向外扩张状态。由此可见,凹凸槽高度对液滴撞击凹凸槽液膜形态变化的显著影响。

|
Download:
|
| 图 5 液滴撞击不同槽道高度表面液膜的运动演变过程 Fig. 5 Evolution of a droplet impact into liquid film with rectangular groove height | |
为进一步讨论液滴撞击凹凸槽液膜后变化规律,本文对水花高度H和水花直径D进行对比。从图 6(a)可以看出,撞击后水花的高度先增加后减小。对比h为0.1和0.3 mm的微槽表面的水花高度发现,0.3 mm槽道的最大水花高度小于0.1 mm槽道的最大水花高度,这是槽道深度的增加使得其对液滴的撞击起到缓冲作用,造成转化为冠状水花的动能减少,进而导致水花高度下降。当槽道高度为0.5 mm时,虽然槽道深度进一步增加,但是槽道顶部上的液膜层厚度减小,使得液膜横向扩展的阻力减小。因此,液滴撞击过程中更易于形成较薄的水花,在瑞利不稳定性的作用下,水花端部卫星液滴的脱离,造成水花回缩,使得水花高度突然降低。从水花直径角度分析,0.3 mm高度槽道的水花直径小于0.1 mm高度槽道的水花直径,槽道高度对水花向两侧传递起着抑制作用,而0.5 mm槽道的水花直径先增大后减小,即水花先向外扩张,达到6 ms后开始收缩。而脱离的二次液滴,带走更多的动能,液膜向外扩张的驱动力减弱,导致液膜迅速回缩。槽道高度会影响冠状水花高度和宽度的演变,并决定卫星液滴的生成。槽道高度改变了液滴动能向冠状水花和液膜传递的相对大小,并存在一个产生卫星液滴的临界微槽高度。

|
Download:
|
| 图 6 槽道高度对液膜的水花高度H和水花直径D的影响 Fig. 6 Effects of the rectangular groove height on the crown height H and diameter D | |
为进一步研究微槽高度的影响,将h增加至0.8、1和1.1 mm(液膜均为高度1 mm),分别对应图 7(a)、7(b)、7(c)。对比图 7(a)、7(b)、7(c)可以看出,槽道高度略低于液膜时,液滴撞击液膜产生较薄的水花,二次液滴生成数量增加,半径减小。槽道与液膜齐平(b)和槽道高于液膜(c),都抑制冠状水花的生成,对于槽道与液膜齐平时,液滴在固液间隔表面上平铺回缩,液滴外沿部分接触到液膜,在表面张力的作用下,会有部分液滴融入槽道中的液膜,发生动量交换,在整个过程中没有飞溅现象。当槽道高于液膜时,图 7(c)中,液滴撞击时首先接触槽道,液滴依然平铺回缩,但是在铺展过程中,液滴在槽道和液膜共同作用下被切割成几部分,液滴回缩阶段,在表面张力的作用下,分割开的几部分薄液膜会聚合在一起,形成中间大、两端小的分液滴。

|
Download:
|
| 图 7 槽道高度高于表面液膜时液滴撞击液膜运动演变过程 Fig. 7 Evolution of a droplet impact into liquid film when the height of groove is higher than liquid film | |
图 8(a)、8(b)、8(c)槽道宽度分别为0.3、0.5、1.0 mm,槽道高度为0.5 mm,槽道间距等于槽道宽度。由图 8看出,槽道宽度增加,冠状水花都出现了飞溅现象,即都有二次液滴的出现,但出现的时间略有不同。对于宽0.5 mm凹凸槽,二次液滴出现大约在2.4 ms之后,而对于0.3 mm凹凸槽,二次液滴出现大约在2.8 ms之后。对于1 mm宽凹凸槽,二次液滴的出现大约在3.2 ms之后。撞击2 ms之后,可以看出对应于宽1 mm凹凸槽模拟形态中,凹凸槽上方,水花中部有液团出现,初始并不明显,呈平铺状态,直到6 ms时,液团开始向内汇聚,向上拱起呈子弹形状,形态非常明显,到10 ms左右又开始向下回落。而这在0.3和0.5 mm宽凹凸槽模拟形态中并未出现,可以看到,0.3和0.5 mm凹凸槽模拟形态中水花中部液团一直呈平铺状态,且十分薄,形态不明显。造成该差异的主要原因有两点,一是当槽道较宽时,槽道内液体对撞击过程中能量的吸收使得表层液膜向外扩展的能力略微下降,如图 8(b)所示。另外,也使得撞击点处易于形成较厚的液膜,为后续形成液团提供了基础;二是随着槽道宽度的增加,槽道顶端液膜的流动对槽道内液体的影响也越来越突出,由于槽道中液体与上部液体的接触面积和时间的增加,使得槽道内液体的流动加剧,进而使得槽道中部分液体有溢出槽道的倾向,如在8.6 ms时。因此,也造成了铺展过程中在靠近撞击点侧的槽道处,出现液体之间的分割,使得撞击中心处出现独立液团。此外,凹凸槽宽度对液滴碰撞形态后之间的相互差异的影响相比高度的影响较低。
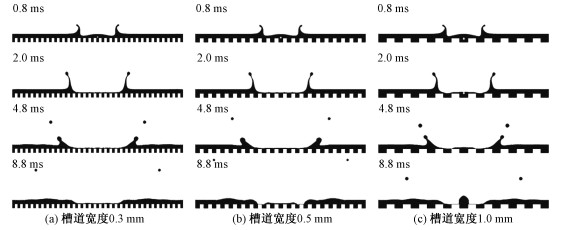
|
Download:
|
| 图 8 液滴撞击不同槽道宽度表面液膜的运动演变过程 Fig. 8 Evolution of a droplet impacts into liquid film at different rectangular groove width | |
为进一步探查凹凸槽宽度对液滴撞击液膜形态的影响,本文同样对水花高度H和水花直径D做了对比。如图 9所示,凹凸槽高度对水花高度H和水花直径D的影响比较小,只在水花高度和二次液滴的脱离时间方面有所不同,槽道宽度对水花直径没有影响。
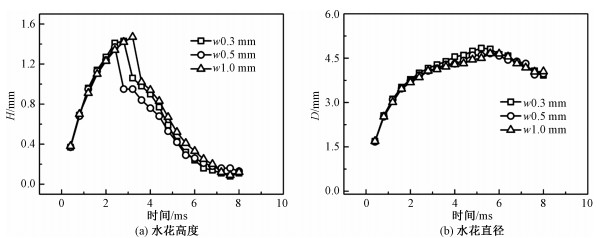
|
Download:
|
| 图 9 槽道宽度对液膜的水花高度H和水花直径D的影响 Fig. 9 Effects of the rectangular groove width on the crown height H and diameter D | |
We数表示惯性力与表面张力之比,其定义为We=ρv2d/σ,v是液滴速度,d是液滴直径,σ是表面张力系数,槽道宽0.3 mm,高0.5 mm,间距0.3 mm。图 10为水花高度和水花直径随We数的变化情况,Re数为373。图 10(a)中水花高度均是先增加后下降,在3 ms左右达到最大值,且We数越大,最大水花高度越大。当We数为235时,由于没有二次液滴的生成,水花高度变化平缓,当We数增大,出现二次液滴脱离,图 10(a)所示,在2.8 ms时,由于二次液滴的脱离造成水花高度迅速下降,且We越大,分离的二次液滴越多。We数越大,液滴具有的动能增大,水花需要更长的时间才能降落稳定。对于水花直径,如图 10(b)所示,水花直径先增大后减小,这是由于液滴撞击引起液膜向两端扩展,达到最大值后,较高的液膜向低处液膜流动,水花直径减小。We数越大,水花直径的最大值越大,并且水花高度和水花直径并不是同一时刻达到最大值。
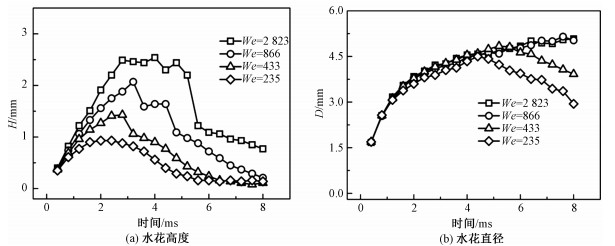
|
Download:
|
| 图 10 We数对液膜的水花高度H和水花直径D的影响 Fig. 10 Effects of the We number on the crown height H and diameter D | |
1) 存在一个槽道高度临界值,槽道高度小于这个值时,冠状水花的高度和直径随着槽道高度的增加而减小,且没有二次液滴的生成。当槽道高度高于临界值时,液滴撞击液膜后产生的冠状水花厚度变薄,有利于产生二次液滴,冠状水花持续时间变短。当槽道高于液膜时,在液滴撞击的铺展回缩过程中,槽道和液膜起到分割液滴的作用。
2) 槽道宽度对水花高度H和水花直径D的影响比较小,只在水花高度和二次液滴的脱离时间方面有所不同,且最大水花高度没有规律可循,槽道宽度对水花直径没有影响。
3) We数越大,代表液滴具有的动能越大,撞击液膜后产生的水花高度增加,水花直径增大,液膜界面波动越剧烈,且迅速向两侧传递。同时We数增加导致分离的二次液滴数量增多。
| [1] |
Yarin A L. Drop impact dynamics:splashing, spreading, receding, bouncing[J]. Annual Review of Fluid Mechanics, 2006, 38(1): 159-192. Doi:10.1146/annurev.fluid.38.050304.092144 |
| [2] |
Liang G, Mudawar I. Review of mass and momentum interactions during drop impact on a liquid film[J]. International Journal of Heat and Mass Transfer, 2016, 101: 577-599. Doi:10.1016/j.ijheatmasstransfer.2016.05.062 |
| [3] |
王锐, 景青, 周致富, 等. 甘油/压缩空气两相喷雾动力学研究[J]. 中国科学院大学学报, 2016, 33(2): 223-227. |
| [4] |
张雷刚, 陈振乾. 针柱诱导铝表面冷凝液滴聚并的实验研究[J]. 中国科学院大学学报, 2018, 35(2): 227-232. |
| [5] |
Wang A B, Chen C C. Splashing impact of a single drop onto very thin liquid films[J]. Physics of Fluids, 2000, 12(9): 2155-2158. Doi:10.1063/1.1287511 |
| [6] |
Wal R L V, Berger G M, Mozes S D. Droplets splashing upon films of the same fluid of various depths[J]. Experiments in Fluids, 2006, 40(1): 33-52. Doi:10.1007/s00348-005-0044-2 |
| [7] |
Chen N, Chen H, Amirfazli A. Drop impact onto a thin film:miscibility effect[J]. Physics of Fluids, 2017, 29(9): 092106-092113. Doi:10.1063/1.5001743 |
| [8] |
Dai J F, Fan X P, Meng B, et al. A coupled level-set and volume-of-fluid simulation for splashing of single droplet impact on an inclined liquid film[J]. Acta Physica Sinica, 2015, 64(9): 94704. |
| [9] |
Shetabivash H, Ommi F, Heidarinejad G. Numerical analysis of droplet impact onto liquid film[J]. Physics of Fluids, 2014, 26(1): 179-200. |
| [10] |
王小永, 郭加宏, 张崇明. 液滴冲击流动液膜的格子Boltzmann模拟[J]. 水动力学研究与进展:A辑, 2011, 26(4): 501-508. |
| [11] |
郭亚丽, 张京涛, 沈胜强, 等. 双液滴同时撞击液膜的动力学演变[J]. 哈尔滨工程大学学报, 2016, 37(6): 796-801. |
| [12] |
Liang G, Guo Y, Yang Y, et al. Spreading and splashing during a single drop impact on an inclined wetted surface[J]. Acta Mechanica, 2013, 224(12): 2993-3004. Doi:10.1007/s00707-013-0910-6 |
| [13] |
Liang G, Shen S, Mu X. Numerical analysis and insight of drop impacting dynamics upon a liquid film[J]. Acta Mechanica, 2017, 228(2): 385-400. Doi:10.1007/s00707-016-1704-4 |
| [14] |
Hao C, Li J, Liu Y, et al. Superhydrophobic-like tunable droplet bouncing on slippery liquid interfaces[J]. Nature Communications, 2015, 6: 7986-7993. Doi:10.1038/ncomms8986 |
| [15] |
Kreder M J, Alvarenga J, Kim P, et al. Design of anti-icing surfaces:smooth, textured or slippery?[J]. Nature Reviews Materials, 2016, 1(1): 15003-15018. Doi:10.1038/natrevmats.2015.3 |
| [16] |
Wong T S, Kang S H, Tang S K Y, et al. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity[J]. Nature, 2011, 477(7365): 443-447. Doi:10.1038/nature10447 |
| [17] |
Guo C, Zhao D, Sun Y, et al. Droplet impact on anisotropic superhydrophobic surfaces[J]. Langmuir the Acs Journal of Surfaces & Colloids, 2018, 34(11): 3533-3540. |
 2020, Vol. 37
2020, Vol. 37 


