近几十年能源消耗量不断增加,CO2排放量急剧上升,从而引发了温室效应等一系列的环境问题。从排放源来看,中国火力发电CO2排放量约占工业CO2总排放量的近50%[1],因此分离和捕集火力发电厂烟道气中的CO2成为控制CO2排放最有效的手段之一。火电厂烟道气往往排放温度较高(100 ℃左右)、CO2体积比仅约10%~15%,且含有水蒸气等杂质性气体成分。针对此特点,金属氧化物及其盐类通常可在较高温度下吸附CO2,且能够耐受一定的水蒸气,因此是一种非常理想的CO2吸附剂。在金属氧化物及其盐类材料中,Mg由于在自然界中储量大,MgO易于制取,可在200 ℃以下吸附CO2,因此相对于CaO吸附剂和锂盐吸附剂,MgO吸附剂的CO2吸附温度在200 ℃以下,是一种非常适于捕集电厂烟道气中CO2的吸附剂。
现阶段对于MgO吸附剂的研究多在于实验方面,包括提高比表面积[2]、优化孔道结构[3]、获得颗粒成型方法[4]及其对材料吸附性能的影响等,如Bian等[5]采用热分解法制备介孔MgO材料,和市面所售相比具有更大的比表面积和更高的吸附量;Song等[6]通过煅烧法合成介孔MgO材料,其比表面积大,吸附选择性好;闻霞等[7]采用等体积浸渍法制取MgO/Al2O3吸附剂,获得MgO负载量、吸附温度等因素对吸附剂吸附CO2性能的影响;陈林等[4]制备碳参杂MgO颗粒,具有较好的机械强度与较高的比表面积。但现阶段缺少数值模拟的手段分析吸附过程中多孔MgO颗粒内烟道混合气体的渗流及CO2传输反应特性。
格子Boltzmann方法(lattice Boltzmann method, LBM)作为一种基于动理学的介观尺度数值理论,其粒子背景使得该方法在单组分流动、传热传质、多组分多相流动、多孔介质内流动等领域有着广泛的应用[8-10]。国内外已经利用该方法开展了大量气固反应的数值模拟研究工作,如:Sullivan等[11]利用格子Boltzmann方法开展反应床尺度流动与传质的耦合建模,且该模型适用于低扩散系数、高贝克莱数情况。张婷等[12]利用格子Boltzmann方法对孔隙尺度下碱性金属氧化物CaO吸收CO2过程进行模拟,分析摩尔体积比与达姆科勒数对CaO转化率的影响。Bohn等[13]利用LBM法对CO与Fe2O3还原反应进行模拟,结果与实验数据吻合很好。Zhou等[14]利用格子Boltzmann方法研究孔隙尺度下气体在固体表面吸附过程,并分析气相速度分布及孔隙率对吸附平衡态的影响。已有研究针对MgO颗粒吸附法捕集电厂烟道气中CO2的相关研究甚少,因此本文从表征体元(representative elementary volume, REV)尺度出发,采用格子Boltzmann方法对含化学反应的单颗粒多孔MgO吸附剂吸附CO2的过程进行数值模拟研究,其中假设颗粒为规则球体,混合气体由N2与CO2组成,吸附过程绝热,基于二级反应动力学模型研究单颗粒多孔MgO内CO2的传输特性,分析孔隙率与颗粒粒径变化对于颗粒内渗流速度、CO2吸附速率及MgO颗粒转化率的影响。
1 格子-Boltzmann模型 1.1 流动格子-Boltzmann模型本文采用Guo和Zhao[15]提出的表征体元尺度下渗流广义LBE模型模拟单颗粒多孔MgO吸附剂内主体气体(N2)的流动过程,并采用D2Q9格子模型,其控制方程为
| $ \begin{array}{*{20}{c}} {{f_i}\left( {r + {e_i}{\delta _t},t + {\delta _t}} \right) - {f_i}\left( {r,t} \right) = }\\ { - \tau _{\rm{v}}^{ - 1}\left( {{f_i}\left( {r,t} \right) - f_i^{eq}\left( {r,t} \right)} \right) + {\delta _t}{F_i},} \end{array} $ | (1) |
式中:fi(r, t)为网格点r处t时刻粒子的分布函数;δt为时间步长;i=0~8;ei为粒子离散速度,e0=0,e1=-e3=(1, 0)c,e2=-e4=(0, 1)c,e5=-e7=(1, 1)c,e6=-e8=(-1, 1)c;其中c为格子速度, c=δx/δt,δx为格子步长, τv为流动格子方程的无量纲松弛时间。速度的平衡态分函数为
| $ f_i^{{\rm{eq}}}\left( {r,t} \right) = {\omega _i}\rho \left[ {1 + \frac{{{e_i}U}}{{c_{\rm{s}}^2}} + \frac{{UU:\left( {{e_i}{e_i} - c_{\rm{s}}^2I} \right)}}{{2\varepsilon c_{\rm{s}}^4}}} \right], $ | (2) |
外力项Fi定义为
| $ {F_i} = {\omega _i}\rho \left( {1 - \frac{1}{{2{\tau _{\rm{s}}}}}} \right)\left[ {\frac{{{e_i} \cdot F}}{{c_s^2}} + \frac{{UF:\left( {{e_i}{e_i} - c_{\rm{s}}^2I} \right)}}{{\varepsilon c_{\rm{s}}^4}}} \right]. $ | (3) |
式中:当地声速为cs;ε为孔隙率;ωi为权系数,ω0=4/9,ωi=1/9(i=1~4),ωi=1/36(i=5~8);F是包含有外力和介质阻力的合力,其表达式为
| $ F = - \frac{{\varepsilon v}}{K}U - \frac{{\varepsilon {F_s}}}{{\sqrt K }}\left| U \right|U + \varepsilon \mathit{\boldsymbol{G}}, $ | (4) |
式中:υ为流体运动黏度; G为外部体积力; K为渗透率; Fε为结构参数,利用Ergun方程得到:
| $ K = \frac{{{\varepsilon ^3}{d^2}}}{{150{{\left( {1 - \varepsilon } \right)}^2}}},{F_\varepsilon } = \frac{{1.75}}{{\sqrt {150{\varepsilon ^3}} }}. $ | (5) |
渗流的密度ρ与宏观渗流速度U定义为
| $ \rho = \sum {{f_i}} ,U = \frac{v}{{{a_0} + \sqrt {a_0^2 + {a_1}\left| v \right|} }}. $ | (6) |
式中速度v为一个临时速度,公式为
| $ v = \sum {{e_i}} {f_i}/\rho + \frac{{{\delta _t}}}{2}\varepsilon \mathit{\boldsymbol{G}}. $ | (7) |
a0,a1为参数,其取值为:
| $ {a_0} = \frac{1}{2}\left( {1 + \varepsilon \frac{{{\delta _t}}}{2}\frac{v}{K}} \right),{a_1} = \varepsilon \frac{{{\delta _t}}}{2}\frac{{{F_\varepsilon }}}{{\sqrt K }}. $ | (8) |
对式(1)做Chanpman-Enskog多尺度展开得到其对应的宏观动量方程如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho U} \right) = 0, $ | (9) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial (\rho U)}}{{\partial t}} + \nabla \cdot \left( {\frac{{\rho UU}}{\varepsilon }} \right) = - \nabla (\varepsilon p) + }\\ {\nabla \cdot \left[ {\rho {v_{\rm{e}}}(\nabla U + U\nabla )} \right] + F.} \end{array} $ | (10) |
式中:压力p=cs2ρ/ε, 有效黏度系数υe=cs2(τ-0.5)δt。
1.2 传质格子-Boltzmann模型 1.2.1 传质模型利用格子Boltzmann传质模型模拟多孔MgO颗粒内的CO2流动传输与吸附过程。CO2溶质视为被动标量,认为其与主体气体(N2)之间是单向作用,溶质的对流扩散过程不影响主体气体N2的流动。根据Zeiser等[16]的研究,在不影响计算精度的情况下,可将速度离散方向由9个降为5个(D2Q9模型变为D2Q5模型,i取0~4),其控制方程为
| $ \begin{array}{*{20}{c}} {{g_i}\left( {r + {c_i}\delta t} \right) - {g_i}(r,t) = }\\ { - \frac{1}{{{\tau _{\rm{c}}}}}\left( {{g_i}(r,t) - g_i^{{\rm{eq}}}(r,t)} \right) + {J_i}{\delta _t}R.} \end{array} $ | (11) |
式中:gi为溶质浓度的分布函数,τc为传质格子方程的无量纲松弛时间,R为反应源项,Ji为常数。二维情况下Ji=J0(i=0),Ji=(1-J0)/4(i=1~4),J0为可调参数,0≤J0≤1,geq为浓度的平衡态分布函数, 公式为
| $ g_i^{{\rm{eq}}}\left( {r,t} \right) = C\left( {{J_i} + \frac{1}{2}\frac{{{e_i}U}}{{{c^2}}}} \right). $ | (12) |
对浓度分布函数gi求和可以获得其浓度
| $ C = \sum {{g_i}} . $ | (13) |
与流动方程一样,对式(11)做Chanpman-Enskog多尺度展开得到其宏观的传质对流扩散方程
| $ \frac{{\partial C}}{{\partial t}} + U\nabla C = D{\nabla ^2}C + R. $ | (14) |
式中,扩散系数为
| $ D = {\delta _t}{c^2}{C_Q}\left( {1 - {J_0}} \right)\left( {{\tau _{\rm{m}}} - 0.5} \right). $ | (15) |
固体MgO颗粒吸附CO2过程是在其表面进行,酸性CO2气体与MgO上的碱性位点O2-发生反应,生成了单齿碳酸根、双齿碳酸根[17]。考虑到反应本身的复杂性,将该反应视为基元反应,颗粒内每个网格节点为反应位点,并参考Bohn等[13]采用二级反应动力学模型对传质源项进行处理:
| $ R\left( {r,t} \right) = \frac{{{\rm{d}}C\left( {r,t} \right)}}{{{\rm{d}}t}} = - {k_{\rm{c}}}C\left( {r,t} \right)\left( {1 - X\left( {r,t} \right)} \right), $ | (16) |
| $ \frac{{{\rm{d}}n\left( {{\rm{r}},t} \right)}}{{{\rm{d}}t}} = \frac{{{\rm{d}}C\left( {{\rm{r}},t} \right)}}{{{\rm{d}}t}}. $ | (17) |
式中:kc为二级反应常数;C(r, t)为CO2气体浓度;n(r, t)为t时刻r节点处的固体浓度;X(r, t)表示MgO颗粒的转化率,其值等于已反应的固体量与初始固体量之比:$X(r, t)=1-\frac{n(r, t)}{n(r, 0)}$。
2 模型验证及边界条件 2.1 流动耦合传质模型的验证对二维矩形通道内充满多孔介质的Poiseuille流动及传质过程进行模拟,其沿Y轴方向的高度为H,沿X轴方向最大流速为U0,已知其流动宏观控制方程为
| $ \frac{{{v_{\rm{e}}}}}{\varepsilon }\frac{{\partial {u^2}}}{{\partial {y^2}}} + G - \frac{v}{K}U - \frac{{{F_\varepsilon }}}{{\sqrt K }}{U^2} = 0. $ | (18) |
式(18)的解析解为
| $ U = GK/v \times (1 - \cosh (\gamma (Y - H/2))/\cosh (\gamma H/2)), $ | (19) |
| $ {U_0} = GK/v \times \left( {1 - {{\cosh }^{ - 1}}(\gamma H/2)} \right). $ | (20) |
式中:γ=(υε/Kυe)。假设通道的上、下壁面浓度为定值,分别为Cu=1.0、Cb=0.0,则对流扩散方程解析解为
| $ C = \frac{{{C_{\rm{u}}} - {C_{\rm{b}}}}}{{{{\rm{e}}^{UH/D}} - 1}}{{\rm{e}}^{UH/D}} + \frac{{{C_{\rm{b}}}{{\rm{e}}^{UH/D}} - {C_{\rm{u}}}}}{{{{\rm{e}}^{UH/D}} - 1}}. $ | (21) |
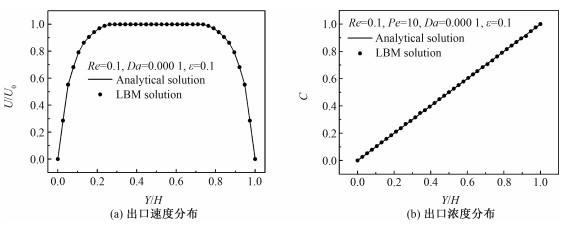
模拟中,矩形计算域采用的网格数为76×76,参数设定为:ε=0.1,Da=0.000 1,Re=0.1,Sc=100。图 1(a)和图 1(b)分别为出口处,沿Y方向速度和浓度的分布曲线,结果表明采用格子Boltzmann方法得到的模拟果与数值解吻合得很好。
|
Download:
|
| 图 1 出口处沿Y轴方向速度和浓度的分布曲线 Fig. 1 The velocity(a) and concentration(b) profiles along the Y-direction at the outlet | |
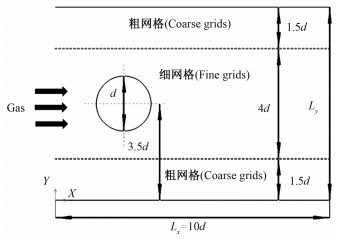
为节省计算时间,本文采用多块网格技术,将计算域划分为上中下3个部分,其上、下部分均为粗网格,中间部分为细网格,计算域为二维矩形计算域,颗粒的无量纲直径为d,X轴方向无量纲长度Lx为颗粒直径d的7倍,Y轴方向无量纲长度Ly为颗粒直径d的10倍,混合气体(N2与CO2组成)沿X轴方向流入,图 2为计算域示意图。
|
Download:
|
| 图 2 计算域示意图 Fig. 2 Computational domain diagram | |
初始条件:参照课题组前期实验结果[18],N2分压0.85 bar,CO2分压0.15 bar, 气体宏观温度取50 ℃,N2密度0.895 1 kg/m3,CO2浓度5.64 mol/m3,MgO颗粒密度3.58 g/cm3(浓度为89 500 mol/m3),入口气体速度0.5 m/s,入口N2密度、浓度及速度均保持恒定。粒径dp1=100 μm,参考长度Xc1=5×10-6 m,参考速度Uc=0.1 m/s,参考浓度Cc=5.64 mol/m3, 参考密度ρc=1.053 kg/m3。当粒径发生变化时,改变参考长度(计算域大小相应变化,但其无量纲值不变,其余物理量值不变)。对于参考量取值与无量纲换算见表 1。通过计算可知粒径dp1=100 μm时,Re=3.2,粒径dp2=200 μm时,Re=6.4,粒径dp3=400 μm时,Re=12.8,施密特数均为Sc=υp/Dp=0.96。
|
|
表 1 物理参数的无量纲转化表 Table 1 Non-dimensional transformation table for physical parameters |
边界条件:入口处N2密度与速度恒定,采用Zou、He入口边界;上、下边界处认为速度边界层已充分发展,沿Y方向速度不再变化,采用非平衡外推格式;出口认为速度不再变化,仍采用非平衡外推格式。对于浓度边界,入口CO2浓度不变,采用恒定浓度边界;上、下及出口边界处认为浓度梯度为零,同采用非平衡外推格式。
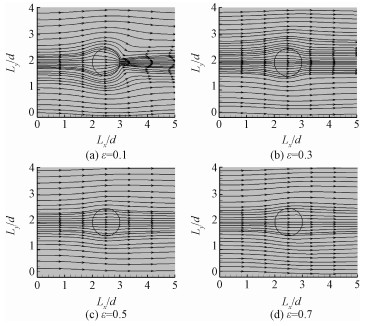
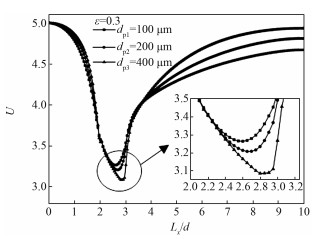
3 结果分析 3.1 粒径大小影响图 3为粒径dp2=200 μm时不同孔隙率下的局部流场图,从图中可以看到孔隙率不同时流线穿过MgO颗粒的偏折程度也不同,孔隙率越小流线偏折越厉害,迂曲度越大;由于流动本身雷诺数较小,所以不存在尾涡与气体回流。流场结构的差异与流速的不同会直影响到对流传质过程,进而影响颗粒内气体浓度,并最终影响气体与固体的反应吸附。图 4为不同粒径下通过圆心截面速度的分布情况,可以看出当粒径较小(dp1=100 μm)时,颗粒内的主流体速度越大且其最小速度越接近球心;颗粒粒径越大时,颗粒内速度越小,且其最小速度越靠近沿流动方向颗粒的后部。
|
Download:
|
| 图 3 不同孔隙率下局部流场分布情况 Fig. 3 Local streamline distribution at different porosities | |
|
Download:
|
| 图 4 不同粒径下通过圆心截面处速度分布 Fig. 4 Velocity distribution along the X-direction through the center of the particle with different sizes | |
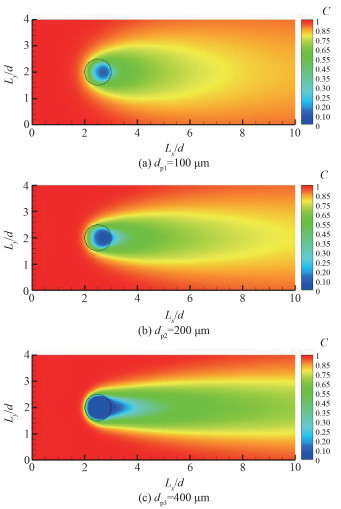
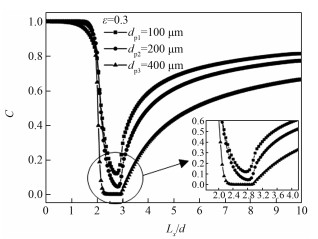
图 5为不同粒径下,t=1.0 s,ε=0.3时细网格计算域内浓度分布云图;图 6为不同粒径下通过圆心截面处沿X轴方向的浓度分布。通过图 5和图 6可以看到,粒径越小颗粒内平均浓度值越大;并且随着颗粒直径的增大,CO2最低浓度位置逐渐沿流动方向向颗粒后部移动。这是由于入口初始速度相同,相同孔隙率下粒径越大,流动阻力越大,颗粒内流速越小,对流传质越弱,传质阻力增加,自然颗粒内浓度值更低。
|
Download:
|
| 图 5 相同时间不同粒径下细网格内CO2浓度分布 Fig. 5 CO2 concentration distribution in fine grids at the same time with different particle sizes | |
|
Download:
|
| 图 6 不同粒径下通过圆心截面CO2浓度分布 Fig. 6 CO2 concentration distribution along the X-direction through the center of the particle with different sizes | |
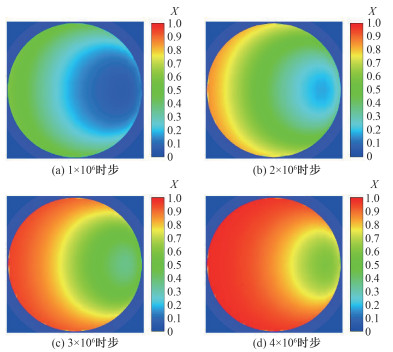
图 7为粒径dp2=200 μm孔隙率为0.5时,不同时步MgO颗粒内固体转化率X (r, t)的分布情况,可以看出由于CO2气体浓度分布的不均匀,固体颗粒的转化率也不均匀,颗粒内沿流动方向颗粒前部浓度较高,其局部固体转化率也更高,由于其本身雷诺数较小,不存在尾涡与气体回流,而颗粒靠后处的流动及传质阻力最大所以浓度最低点及转化率最低点均出现在沿流动方向颗粒后部。
|
Download:
|
| 图 7 不同时步下颗粒内固体转化率分布情况 Fig. 7 Adsorbent conversion rate distributions in particle at different calculation time steps | |
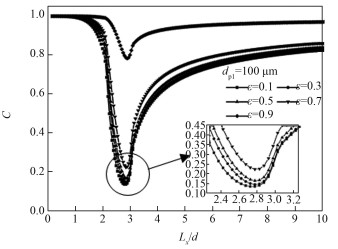
图 8为粒径dp1=100 μm,相同计算时步,不同孔隙率下通过颗粒球心截面处CO2气体浓度的分布情况。从图 8可以发现,同一粒径、相同计算时步下,随着孔隙率的增加,颗粒内的CO2浓度越高。主要原因为孔隙率越大导致颗粒内的渗透率越大(Ergun方程算得),气体传输的阻力更小,并且相同粒径时固体的量随孔隙率增加而减小,使相同时步下吸附的CO2气体量更少,CO2在颗粒内更容易聚集,因而MgO颗粒内的CO2浓度越高。
|
Download:
|
| 图 8 不同孔隙率下通过球心截面的CO2浓度分布 Fig. 8 CO2 concentration distribution along the X-direction through the center of the particle with different porosities | |
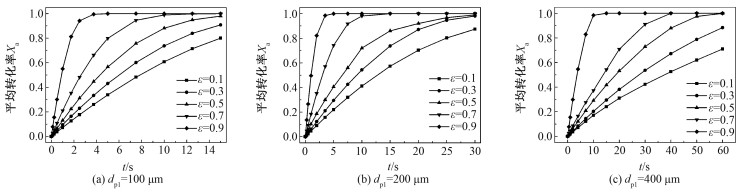
图 9展示粒径分别为100、200和400 μm时孔隙率变化对颗粒内吸附剂平均转化率Xa的影响。由图可知,吸附过程初始阶段,固体转化率较小,转化率随时间基本呈现线性变化;随着时间推移,固体转化率曲线斜率越来越小,这是因为随着反应的进行,MgO颗粒吸附位点不断消耗,虽固体转化率越来越高,但剩余固体的量越来越少,根据反应动力学模型可知吸附速率受到颗粒固体转化率的限制,颗粒的固体转化率变大,反应速率降低,从而导致固体转化率曲线斜率减小,CO2吸附逐渐达到饱和。此外,由前文分析结果知,相同粒径、相同计算时步下,孔隙率的增加使MgO颗粒内CO2浓度升高,根据反应动力学模型可知,CO2浓度越高会导致颗粒内反应位点的吸附反应速率更大,固体的量消耗得更快。以上因素共同作用,导致图 9中相同粒径下,孔隙率越大,反应速率越快,固体颗粒转化率的变化速率越快,CO2达到饱和的过程也越快。
|
Download:
|
| 图 9 不同孔隙率下平均转化率随时间的变化 Fig. 9 Variation in average adsorbent conversion rate with time at different porosities | |
本文从表征体元尺度出发,基于二级反应动力学模型,利用格子Boltzmann方法对单颗粒多孔MgO吸附剂化学吸附CO2过程流动传输特性进行数值模拟,分析孔隙率与颗粒粒径变化对于颗粒内渗流速度、CO2吸附速率及MgO颗粒内固体转化率的影响。主要结论如下:
1) 固体多孔MgO颗粒吸附CO2过程可将吸附位点处理为网格节点,节点处的反应视为基元反应,符合二级反应动力学模型。
2) 沿气体流动方向颗粒内CO2浓度与颗粒转化率逐渐递减;在相同时间下颗粒粒径越大,颗粒内渗流速度越小,CO2浓度越低,转化率越小,吸附速率越慢。
3) 相同粒径和相同时间下,MgO颗粒孔隙率越大,颗粒内CO2浓度越高,MgO固体转化率越高,平均吸附速率越快。
| [1] |
王献红. 二氧化碳捕集和利用[M]. 北京: 化学工业出版社, 2016.
|
| [2] |
Ding Y D, Song G, Zhu X, et al. Synthesizing MgO with a high specific surface for carbon dioxide adsorption[J]. RSC Advances, 2015, 5(39): 30929-30935. Doi:10.1039/C4RA15127E |
| [3] |
Ling Z, Zheng M, Du Q, et al. Synthesis of mesoporous MgO nanoplate by an easy solvothermal-annealing method[J]. Solid State Sciences, 2011, 13(12): 2073-2079. Doi:10.1016/j.solidstatesciences.2010.01.013 |
| [4] |
陈林, 丁玉栋, 朱恂, 等. 高比表面积MgO颗粒制备及其CO2吸附性能研究[J]. 工程热物理学报, 2016, 37(6): 1243-1248. |
| [5] |
Bian S W, Baltrusaitis J, Galhotra P, et al. A template-free, thermal decomposition method to synthesize mesoporous MgO with a nanocrystalline framework and its application in carbon dioxide adsorption[J]. Journal of Materials Chemistry, 2010, 20(39): 8705-8710. Doi:10.1039/c0jm01261k |
| [6] |
Song G, Ding Y D, Zhu X, et al. Carbon dioxide adsorption characteristics of synthesized MgO with various porous structures achieved by varying calcination temperature[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 2015, 470: 39-45. |
| [7] |
闻霞, 孙楠楠, 李碧, 等. MgO/Al2O3吸附剂对CO2动态吸附性能的研究[J]. 燃料化学学报, 2010, 38(2): 247-251. Doi:10.3969/j.issn.0253-2409.2010.02.022 |
| [8] |
Li Q, Luo K H, Kang Q J, et al. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer[J]. Progress in Energy and Combustion Science, 2016, 52: 62-105. Doi:10.1016/j.pecs.2015.10.001 |
| [9] |
杨艳霞, 廖强, 朱恂, 等. 绕流具有光合生化反应管束的格子Boltzmann模拟[J]. 化工学报, 2012, 63(8): 2383-2391. Doi:10.3969/j.issn.0438-1157.2012.08.007 |
| [10] |
马斌, 史琳, 黄超, 等. 孔隙分布不均匀性对渗透率影响的MRTLBM法研究[J]. 中国科学院大学学报, 2018, 35(2): 193-199. |
| [11] |
Sullivan S P, Sani F M, Johns M L, et al. Simulation of packed bed reactors using lattice Boltzmann methods[J]. Chemical Engineering Science, 2005, 60(12): 3405-3418. Doi:10.1016/j.ces.2005.01.038 |
| [12] |
张婷, 郭照立, 柴振华, 等. 钙基吸收剂吸收CO2过程的格子Boltzmann模拟[J]. 化工学报, 2012, 63(S1): 165-171. Doi:10.3969/j.issn.0438-1157.2012.z1.029 |
| [13] |
Bohn C D, Scott S A, Dennis J S, et al. Validation of a lattice Boltzmann model for gas-solid reactions with experiments[J]. Journal of Computational Physics, 2012, 231(16): 5334-5350. Doi:10.1016/j.jcp.2012.04.021 |
| [14] |
Zhou L, Qu Z G, Chen L, et al. Lattice Boltzmann simulation of gas-solid adsorption processes at pore scale level[J]. Journal of Computational Physics, 2015, 300: 800-813. Doi:10.1016/j.jcp.2015.08.014 |
| [15] |
Guo Z, Zhao T S. Lattice Boltzmann model for incompressible flows through porous media[J]. Physical Review E, 2002, 66(3): 036304. Doi:10.1103/PhysRevE.66.036304 |
| [16] |
Zeiser T, Lammers P, Klemm E, et al. CFD-calculation of flow, dispersion and reaction in a catalyst filled tube by the lattice Boltzmann method[J]. Chemical Engineering Science, 2001, 56(4): 1697-1704. Doi:10.1016/S0009-2509(00)00398-5 |
| [17] |
宋淦. MgO吸附剂制备及其CO2吸附性能研究[D].重庆: 重庆大学, 2016.
|
 2020, Vol. 37
2020, Vol. 37 
