正则化算法是处理图像重建等逆问题病态性的重要方法之一[1-3],但是其重建结果受正则化目标函数的惩罚项以及正则化参数的影响很大,且其迭代求解过程耗费很长时间。近些年来,带有稀疏约束的正则化算法在图像处理等领域取得了很大进展[4]。迭代收缩阈值算法(iterative shrinkage thresholding algorithm,ISTA)为该算法的重要方法之一[5-6],由于该算法计算简单,求解时间较短,被广泛应用于逆问题求解中。为了加快其收敛速度,2009年Beck和Teboulle[7]提出一种快速迭代收缩阈值算法(fast iterative shrinkage thresholding algorithm,FISTA),该算法保存了原有算法计算形式的简单性,但在收敛性分析和实验数据上都优于ISTA算法。阈值收缩算子主要包括软阈值收缩算子[8]、硬阈值收缩算子[9]、Firm阈值收缩算子[10]和一些改进的阈值收缩算子[11]等。阈值收缩算子中的阈值参数决定算子中的置零区域和衰减特性的大小,而这两个因素对图像重建的质量具有重要影响。
已有研究表明,当稀疏度较易估计且要求具有较高实时性的逆问题求解中,一般使用硬阈值收缩算子;当对稀疏度难以估计的问题进行求解时,使用软阈值收缩算子;目前使用最多的FISTA算法就是基于软阈值收缩算子的算法之一,但是软阈值收缩算子中的阈值参数在整个迭代过程中始终保持不变,对结果中较大的数据进行衰减,导致最终解偏离真实解,使得图像重建结果中的物体尺寸小于真实分布的物体尺寸,降低重建图像的质量。
针对现有的稀疏正则化算法中阈值参数难以选取的问题,并结合FISTA算法中采用的加速方法[7],提出一种快速自适应阈值迭代算法(fast iterative adaptive thresholding algorithm, FIATA)。该算法中采用的收缩算子的阈值参数在迭代求解过程中能够根据解的稀疏度进行更新;同时为了研究阈值算子的衰减特性对图像重建质量的影响,在该收缩算子中引入权重系数,使得该阈值算子的衰减特性能够调整。考虑电学层析成像(electrical tomography, ET)中被测物场的非连续性,以及其在逆问题求解过程具有严重的非线性和病态性问题[12],稀疏正则化算法被应用到ET逆问题求解中,提高重建图像的质量[13-16]。因此将FIATA算法应用于ET的图像重建中,并与传统的FISTA算法的重建结果进行比较,分别使用仿真和实验验证了该算法的可行性。
1 图像重建算法 1.1 正则化算法图像重建中,测量信号经过处理、计算实现对原始信号的重构,其物理模型的线性化模型一般表示为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}} $ | (1) |
式中:y为测量信号,A为灵敏度矩阵,x为所要重构的信号。
逆问题的求解,即已知测量信号和灵敏度矩阵,求解原始信号。由于灵敏度矩阵具有很高的条件数,导致逆问题的求解具有严重的病态性、欠定性等问题。正则化算法是处理逆问题病态性的重要方法之一,其通用目标函数为
| $ {\mathit{\boldsymbol{x}}_\lambda } = \mathop {argmin}\limits_x \left\{ {\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{b}}} \right\|_2^2 + \lambda G\left( \mathit{\boldsymbol{x}} \right)} \right\}. $ | (2) |
式中:λ为正则化参数,用于调节正则化项G(x)和误差项在目标函数中的比重,根据具体应用的需要设计为不同的形式。
1.2 稀疏正则化算法近些年来,稀疏正则化算法在多个应用领域受到广泛关注,其中以解的l1范数作为正则化项的l1正则化算法研究的最多,其目标函数为
| $ F\left( \mathit{\boldsymbol{x}} \right) = \mathop {argmin}\limits_\mathit{\boldsymbol{x}} \left\{ {\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{b}}} \right\|_2^2 + \lambda {{\left\| \mathit{\boldsymbol{x}} \right\|}_1}} \right\}. $ | (3) |
式中:‖·‖1为向量的$\ell$1范数, 表示为各个元素的绝对值之和。软阈值函数是l1正则化目标函数的最近似映射,其迭代方式和阈值收缩算子[9]表示为:
| $ {\mathit{\boldsymbol{x}}^{n + 1}} = {S_{{\rm{soft}}}}\left( {{\mathit{\boldsymbol{x}}^n} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^n}} \right)} \right). $ | (4) |
| $ {S_{{\rm{soft}}}}\left( {{\mathit{\boldsymbol{x}}^ * }} \right) = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}^*} + \tau ,}&{{\mathit{\boldsymbol{x}}^*} \le - \tau }\\ {0,}&{ - \tau < {\mathit{\boldsymbol{x}}^*} < \tau }\\ {{\mathit{\boldsymbol{x}}^*} - \tau ,}&{{\mathit{\boldsymbol{x}}^*} \ge \tau } \end{array}} \right.. $ | (5) |
式中:x*=xn+AT(b-Axn),xn为上一步的解,τ也是根据经验选取的常量参数,决定软阈值函数置零区域的宽度以及偏移量,与正则化目标函数中的正则化系数λ有着相同的功能,都是用来控制惩罚项惩罚力度的变量。
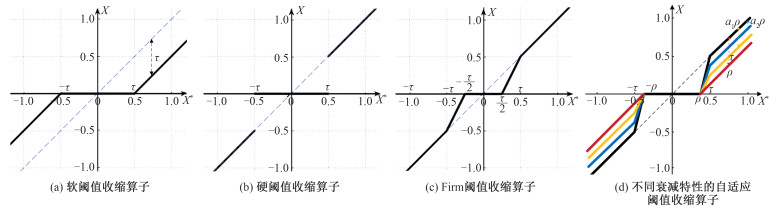
软阈值收缩算子的函数形式如图 1(a)所示。该算子将解中小于τ的值置零,而大于τ的值均有一个绝对值为τ的衰减。对于较大数据的衰减使得在求解过程中会出现重建结果过于稀疏的问题,导致重建图像中内含物的尺寸小于真实被测物场中介质的大小。
|
Download:
|
| 图 1 不同阈值收缩算子示意图 Fig. 1 Different thresholding shrinkage operators | |
为解决软阈值收缩算子对解衰减较大的问题,硬阈值收缩算子被提出。硬阈值函数的最近似映射为$\ell$0正则化,其迭代方式以及硬阈值收缩算子[9]表示为:
| $ {\mathit{\boldsymbol{x}}^{n + 1}} = {S_{{\rm{hard}}}}\left( {{\mathit{\boldsymbol{x}}^n} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^n}} \right)} \right). $ | (6) |
| $ {S_{{\rm{hard}}}}\left( {{\mathit{\boldsymbol{x}}^ * }} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;\left| {{\mathit{\boldsymbol{x}}^ * }} \right| \le \tau \\ {\mathit{\boldsymbol{x}}^ * },\;\;\;\left| {{\mathit{\boldsymbol{x}}^ * }} \right| \ge \tau \end{array} \right.. $ | (7) |
式中:x*=xn+AT(b-Axn),xn为上一步的解,迭代阈值算子τ是根据经验选取的常量参数。
硬阈值收缩算子的函数形式如图 1(b)所示。使用该算子在求解过程中,将解中小于τ的值都置零,而大于τ的值保持不变,解决了软阈值收缩算子中衰减对结果造成的影响问题,但是其对应的目标函数具有严重的非凸特性,导致其在迭代求解过程中不能得到全局最优解。
由于软阈值和硬阈值收缩算子的限制,一个连续的、对迭代过程中较大数据衰减较少的Firm阈值被提出,其迭代格式和收缩算子[10]为:
| $ {\mathit{\boldsymbol{x}}^{n + 1}} = {S_{{\rm{firm}}}}\left( {{\mathit{\boldsymbol{x}}^n} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^n}} \right)} \right). $ | (8) |
| $ {S_{{\rm{firm}}}}\left( {{\mathit{\boldsymbol{x}}^ * }} \right) = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}^*},}&{\left| {{\mathit{\boldsymbol{x}}^*}} \right| \ge \tau }\\ {{\rm{sign}}\left( {{\mathit{\boldsymbol{x}}^*}} \right),}&{\left( {2\left| {{\mathit{\boldsymbol{x}}^*}} \right| - \tau } \right)\tau /2 < \left| {{\mathit{\boldsymbol{x}}^*}} \right| < \tau }\\ {0,}&{\left| {{\mathit{\boldsymbol{x}}^*}} \right| \le \tau /2} \end{array}} \right.. $ | (9) |
式中:x*=xn+AT(b-Axn),xn为上一步的解,τ同样是根据经验选取的常量参数,决定置零区域宽度以及衰减量的大小。
Firm阈值收缩算子的函数形式如图 1(c)所示。使用该算子在迭代求解过程中,将小于阈值τ/2的数据置零,对于τ/2和τ之间的数据进行一定的衰减,而对大于阈值τ的数据则保持不变,减小了软阈值算子带来的较大衰减的问题,使得计算过程中逐步逼近真实解。但是由于阈值参数τ由经验选取,而且在整个迭代求解过程中始终保持不变,使得重建图像的质量因选取的阈值和模型的不同而发生变化,成像结果具有很大的不确定性。
2 自适应阈值迭代算法针对上述问题,提出一种可以根据解的稀疏度自适应更新阈值参数的阈值收缩算子。此外,为了研究算子的衰减特性对重建结果的影响,在该算子中引入权重系数。采用该收缩算子的稀疏正则化算法FIATA的迭代形式和收缩算子的函数形式为:
| $ {\mathit{\boldsymbol{x}}^{n + 1}} = {S_{{\rm{varied}}}}\left( {{\mathit{\boldsymbol{x}}^n} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^n}} \right)} \right). $ | (10) |
| $ {S_{{\rm{varied}}}}\left( {{\mathit{\boldsymbol{x}}^*}} \right) = \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}^*} - a\rho ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{\mathit{\boldsymbol{x}}^*}} \right| \ge \tau \\ \frac{{\tau - a\rho }}{{\tau - \rho }}\left( {{\mathit{\boldsymbol{x}}^*} - \rho } \right),\quad \rho \le \left| {{\mathit{\boldsymbol{x}}^*}} \right| < \tau \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \rho \le \left| {{\mathit{\boldsymbol{x}}^*}} \right| < \rho \\ \frac{{\tau - a\rho }}{{\tau - \rho }}\left( {{\mathit{\boldsymbol{x}}^*} - \rho } \right),\;\;\; - \tau \le \left| {{\mathit{\boldsymbol{x}}^*}} \right| < - \rho \\ {\mathit{\boldsymbol{x}}^*} + a\rho ,\quad \;\;\;\;\;\;\;\;\;\;\;\left| {{\mathit{\boldsymbol{x}}^*}} \right| < - \tau \end{array} \right.. $ | (11) |
式中:阈值τ是根据经验选取的常量参数,是影响置零区域宽度及衰减量大小的因素之一;a(0≤a≤1)为权重系数,当权重系数不断增大时,收缩算子对解的衰减也不断增大;ρ是引入的能够在迭代求解过程中不断更新的阈值参数,同样影响置零区域宽度和衰减量的大小。
根据解的稀疏度(非零元素个数),其更新策略可采用如下形式:
| $ \rho = \frac{\tau }{2}\left( {1 + \frac{{{K_i}}}{N}} \right). $ | (12) |
式中:Ki表示第n次迭代所得解中非零元素的个数,N为所有像素点的个数。
对于阈值参数在迭代过程中的更新,当满足解的稀疏度降低、阈值参数增大或满足解的稀疏度增大、阈值参数减小的趋势,则更新策略有效。改变式(12)中Ki的具体表示形式,可以得到不同的更新策略。经过多次测试,不同的更新策略最终取得的结果相似。因此以下结果的更新策略均将采用式(12)的形式。
不同权重系数的自适应阈值收缩算子的函数形式如图 1(d)所示。相比Firm阈值收缩算子,自适应阈值算子能够通过当前迭代解的稀疏度更新阈值,使得每一步求解更精确。同时通过权重系数a控制不同的衰减特性,一定程度上减小了重建结果过于稀疏带来的问题,使得重建结果更接近真实分布。
3 仿真与实验结果 3.1 仿真模型与结果分析由于ET中被测物场的非连续性,以及其在逆问题求解过程中具有严重的非线性和病态性问题,因此可以将FIATA算法用于ET图像重建中,以验证该算法的可行性。仿真研究中,被测物场的背景电导率为1 S/m,内含物电导率为2 S/m。边界测试数据通过COMSOL与MATLAB混合编程实现获得,计算机配置为3.20 GHz的英特尔i5-6500CPU、4 G内存。由于ET图像重建方法属于差分成像,其灵敏度矩阵在满场为均匀电导率时计算获得,且在整个求解过程中没有更新。
为公平比较FISTA算法和提出的FIATA算法,两种算法迭代求解过程中所需要的参数选取保持一致。图 2为使用FISTA算法和具有不同衰减特性的FIATA算法对3种含有不同内含物的模型进行测试的最优重建结果。在最优重建结果的仿真中,初始阈值参数τ=max(ATy)/20,迭代终止条件Tol=0.000 8,预估稀疏度(非零元素个数)K=20%×length(y)。

|
Download:
|
| 图 2 最佳参数条件下不同模型的重建结果 Fig. 2 Reconstructed images with optimal parameters | |
图 2中,两种算法均能对被测物场进行重建。但是使用FIATA算法进行重建的图像质量会随着权重系数的变化而变化。当内含物分布如模型A所示的简单结构时,两种算法的重建结果差异较小;但是对于如模型B和模型C所示的两个或多个目标分布形式,使用FISTA算法重建时,由于在迭代求解过程中阈值参数始终保持不变,对于较大的数据进行衰减,导致解的结果过于稀疏,重建的图像中内含物的尺寸小于真实被测物场中内含物。而采用FIATA算法时,阈值参数随着当前解的稀疏度不断地进行更新,所以其重建的成像结果要明显优于FISTA算法。
为了对算法的重建结果进行定量分析,使用相关系数(correlation coefficient, CC)和相对误差(relative error, RE)两个图像重建性能评价指标,其定义分别为:
| $ {\rm{CC}} = \frac{{\sum\limits_{i = 1}^n {\left( {{{\hat \sigma }_i} - \bar {\hat \sigma} } \right)} \left( {{\sigma _i} - \bar \sigma } \right)}}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{{\hat \sigma }_i} - \bar {\hat \sigma} } \right)}^2}} \sum\limits_{i = 1}^n {{{\left( {{\sigma _i} - \bar \sigma } \right)}^2}} } }}, $ | (13) |
| $ {\rm{RE}} = \frac{{{{\left\| {\hat \sigma - \sigma } \right\|}_2}}}{{{{\left\| \sigma \right\|}_2}}}. $ | (14) |
式中:σ和$\hat{\sigma}$为真实电导率和重建电导率;σi和$\hat{\sigma}$i分别为σ和$\hat{\sigma}$的第i个元素;σ和$\overline {\hat \sigma}$分别为σ和$\hat{\sigma}$的平均值。
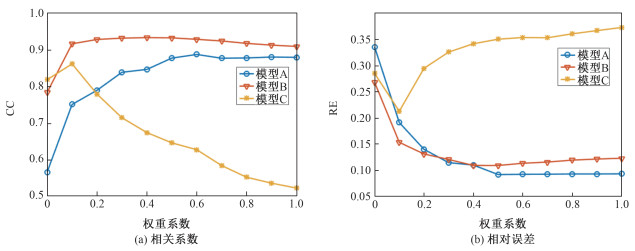
图 3分别为对3种分布模型采用具有不同衰减特性的FIATA算法时重建图像的CC和RE计算结果。
|
Download:
|
| 图 3 不同权重系数重建结果的相关系数和相对误差 Fig. 3 CC and RE of reconstructed images with different weight coefficients | |
图 3中两个性能指标随FIATA算法中自适应阈值收缩算子衰减特性的变化而变化。对于模型A和模型B,随着衰减特性的增强,成像结果的性能指标随之提高;但是当算子的权重系数增加到0.5之后,图像的质量将没有明显的改善。对于被测物场包含4个内含物、结构相对复杂的模型C,当权重系数为0.1时,其成像结果的性能达到最优;当权重系数大于0.1后,随着系数的增大、成像结果的性能降低。仿真结果表明,当重建内含物分布如模型A和模型B所示的简单结构时,FIATA算法中宜采用较大的权重系数;对于如模型C所示的具有相对复杂的内含物分布,FIATA算法中使用较小的权重系数能够提高重建结果的质量。
3.2 实验结果为进一步验证FIATA算法对于求解逆问题的有效性以及衰减特性对于图像重建质量的影响,采用ET实验系统进行测试。测试系统为16电极传感器,相邻激励、相邻测量工作模式。被测场模型的背景介质是电导率为0.06 S/m的自来水,内含物是电导率为10-12 S/m的尼龙棒。分别对图 4所示的3种分布模型进行测试,并使用FISTA算法和权重系数为0.1和0.5的FIATA算法进行重建,并对重建结果进行定量分析,其性能指标如表 1所示。

|
Download:
|
| 图 4 实测系统的重建结果 Fig. 4 Reconstructed images for the experimental system | |
|
|
表 1 不同算法重建结果的性能指标 Table 1 Comparison of performance of reconstructed results among different algorithms |
图 4所示的内含物分布图像重建结果中,采用具有衰减特性的FIATA算法重建的成像结果的质量相比于传统的FISTA算法有所提高。表 1中,实验与仿真所获得的图像重建的性能(图 3所示)基本一致;当使用FIATA算法时,对于被测物场内含物分布相对简单的模型M1和模型M2,选用权重系数为0.5的收缩算子时,所重建的图像性能指标优于FISTA算法;对于内含物分布较复杂的模型M3,选用权重系数为0.1的收缩算子时,重建结果的性能指标比FISTA算法有所提高。因此在实际测量中,根据被测物场中内含物分布复杂程度的在线估计,选择FIATA算法的权重系数,能够获得较高的重建图像质量。
4 结论为了改善稀疏正则化算法中阈值参数难以选取的问题,提出FIATA算法。该算法中采用的收缩算子通过在求解过程中根据解的稀疏度对阈值参数不断调整,减小了传统收缩算子对解的过惩罚,以求得更精确的解,提高重建图像的质量。通过在该算子中引入权重系数,研究收缩算子的衰减特性对图像重建质量的影响。当被测物场的内含物分布较为简单时,采用较大的权重系数,对解进行大的衰减;当被测物场的内含物分布相对复杂时,通过使用较小的权重系数,对解进行较小程度的衰减,提高重建图像的质量。
使用仿真和实验分别验证FIATA算法的可行性,该算法有望应用于其他模态的图像重建中,同时能够用于其他具有病态性的逆问题求解中。在未来的工作中,需进一步降低选取权重系数对被测物场内含物分布复杂程度在线估计的依赖,研究权重系数自适应选取的方法,提高FIATA算法的自适应能力。
| [1] |
Schroter T, Tautenhahn U. On the optimality of regularization methods for solving linear ill-posed problems[J]. Journal for Analysis and its Application, 1994, 13(4): 697-710. |
| [2] |
Xu Y B, Pei Y, Dong F. An adaptive Tikhonov regularization parameter choice method for electrical resistance tomography[J]. Flow Measurement and Instrumentation, 2016, 50: 1-12. Doi:10.1016/j.flowmeasinst.2016.05.004 |
| [3] |
陈晓艳, 房晓东. 一种新的正则化图像重建算法及参数优化[J]. 天津科技大学学报, 2014, 29(6): 74-77. |
| [4] |
Natarajan B K. Sparse approximate solutions to linear systems[J]. Society for Industrial and Applied Mathematics, 1995, 24(2): 227-234. |
| [5] |
Daubechies I, Defrise M, De Mol C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457. Doi:10.1002/cpa.20042 |
| [6] |
Bioucas-Dias J, Figueiredo M. A new TwIST:two-step iterative shrinkage/thresholding algorithms for image restoration[J]. IEEE Transactions on Image Processing, 2007, 16(12): 2992-3004. Doi:10.1109/TIP.2007.909319 |
| [7] |
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. Doi:10.1137/080716542 |
| [8] |
Blumensath T, Davies M E. Iterative thresholding for sparse approximations[J]. Journal of Fourier Analysis and Applications, 2008, 14(5/6): 629-654. Doi:10.1007/s00041-008-9035-z |
| [9] |
Bredies K, Lorenz D A. Iterated hard shrinkage for minimization problems with sparsity constraints[J]. SIAM Journal on Scientific Computing, 2008, 30(2): 657-683. Doi:10.1137/060663556 |
| [10] |
Fornasier M, Rauhut H. Iterative thresholding algorithms[J]. Applied Computational Harmonic Analysis, 2008, 25(2): 187-208. Doi:10.1016/j.acha.2007.10.005 |
| [11] |
Voronin S, Woerdeman H J. A new iterative firm-thresholding algorithm for inverse problems with sparsity constraints[J]. Applied Computational Harmonic Analysis, 2013, 35(1): 151-164. Doi:10.1016/j.acha.2012.08.004 |
| [12] |
Dickin F, Wang M. Electrical resistance tomography for process applications[J]. Measurement Science and Technology, 1996, 7(3): 247-260. Doi:10.1088/0957-0233/7/3/005 |
| [13] |
Gehre M, Kluth T, Lipponen A, et al. Sparsity reconstruction in electrical impedance tomography:an experimental evaluation[J]. Journal of Computational and Applied Mathematics, 2012, 236(1): 2126-2136. Doi:10.1016/j.cam.2011.09.035 |
| [14] |
董峰, 赵佳, 许燕斌, 等. 用于电阻层析成像的快速自适应硬阈值迭代算法[J]. 天津大学学报, 2015, 48(4): 305-310. |
| [15] |
Ye J M, Wang H G, Yang W Q. Image reconstruction for electrical capacitance tomography based on sparse representation[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 89-102. Doi:10.1109/TIM.2014.2329738 |
| [16] |
Zhao J, Xu Y B, Tan C, et al. A fast sparse reconstruction algorithm for electrical tomography[J]. Measurement Science and Technology, 2014, 25(8): 085401. Doi:10.1088/0957-0233/25/8/085401 |
 2020, Vol. 37
2020, Vol. 37 


