多相流广泛存在于自然界和人类生产过程,如能源、动力、冶金、化工、宇航、医药等现代工程领域[1]。其中,油水两相流是在石油、化工等生产过程中广泛存在的一种多相流形式,对其流动状态的掌握和流动参数的获取,是保障生产过程安全稳定运行的前提[2-3]。过程层析成像技术作为一种可视化检测技术,可实现多相流流动状态和流动参数的在线获取。根据激励源能量的种类不同,过程层析成像技术主要有光电法[4]、超声法[5]及射线法[6]等。与光电法和射线法相比,超声层析成像技术由于具有非侵入、无辐射、安装方便等优点,在油水两相流检测中有很好的应用前景。
超声层析成像技术的图像重建是利用超声波在被测场域内基本上是沿直线传播并线性衰减的特性,在接收信号和被测物体间形成基于路径的线性关系。通过比较激励信号和接收信号的幅值差异,获得收发探头间投影路径上声衰减的平均估计,并采用图像重建算法,通过对场域内各位置衰减系数的估计,实现图像重建。
传统的图像重建方法包括线性反投影(linear back projection,LBP)[7]、滤波反投影(filter back projection,FBP)[8]等算法,这一类算法成像实时性高,但重建精度较差,无法实现对油水两相流等弱声阻抗比介质的有效重建。另一类图像重建方法为基于迭代和约束项的算法,如总变差正则化(total variation,TV)[9]、代数重建(algebraic reconstruction technique,ART)[10]、同步迭代重建(simultaneous iteration reconstruction technique,SIRT)[11]等算法,该类算法将被测物场的均匀分布状态作为成像的初始估计值,在每次迭代中加入约束项,实现场域内介质分布的最优搜索,该类算法对噪声有一定的鲁棒性,并能稳定收敛至最优解。
对于广泛存在的弱声阻抗比两相介质,由于其界面透射因数远大于反射因数,通常采用透射模态的成像方法。在透射模态基础上,对低声阻抗比内含物进行较高精度超声重建主要依赖两方面因素:首先是获得包含准确衰减信息的高信噪比边界测试数据,其次是设计高精度的图像重建算法,在满足实时性要求下达到尽可能高的精度和分辨率。事实上,超声成像图像重建的质量一直严重依赖于探头安装数量,过多的探头数量对超声信号收发装置的设计提出了较高的要求,不适用于工业多相流的测量;另一方面,换能器数量的增加大幅提高了图像重建算法中系数矩阵的维度,对系数矩阵的求逆过程占用大量的计算资源和过长的计算时间,使其无法动态反映管道内油水两相流的实时变化情况。
针对采用超声层析成像实现低对比度声学特性的油、水两相介质分布重建问题,提出一种基于高斯回归预测的高分辨率相介质分布图像重建算法。在获取采用超声连续波激励方式的边界测量数据的基础上,提取边界测量声压幅值中包含的超声衰减信息,通过采用能够同时兼顾重建速度和重建精度的基于截断奇异值分解的同步代数迭代重建算法,并构建高斯回归模型,将低分辨率重建结果转化为高分辨率图像。仿真模拟测试结果表明,所提出的算法计算速度快、重建误差小、图像分辨率高,为采用超声层析成像技术实现油水两相流动态可视化检测提供了有效的解决方案。
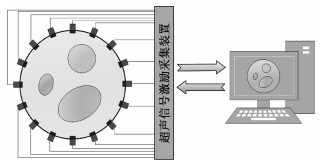
1 超声层析成像原理与数学模型 1.1 超声层析成像原理超声层析成像的基本原理是对收发信号间幅值、相位、时间的差异进行分析,确定内含物的密度、声速、声衰减系数。超声层析成像系统一般包含:超声换能器阵列、超声信号激励采集装置、主控计算机及图像重建算法等部分,组成结构如图 1所示。
|
Download:
|
| 图 1 超声层析成像基本原理 Fig. 1 Basic schematic of ultrasound tomography | |
图 1中,超声换能器阵列由多个超声换能器组成,等间距排布在被测场域的外围并由统一的多路复用器控制激励和采集时序。当选择某一特定探头进行激励时,采用一定幅值的正弦电信号加载在压电晶片两端,产生柱面波形式的超声波振动,接收探头记录相应激励下的声压幅值响应。按照“一发全收”的方式进行循环激励与采集,对每个超声探头分别进行激励以获取不同投影角度的超声幅值响应信息,总计获得N×(N-1)组时变超声信号(N为探头数量),通过采集装置将解调数据发送给主控计算机,重建被测场域衰减系数分布。
1.2 超声层析成像数学模型超声在场域内含物中的衰减过程较为复杂,耦合了散射衰减、扩散衰减和吸收衰减等多种机制。作为各种衰减机制的综合表征,衰减系数是指单位距离内收发声压信号的幅值比例差异。一般意义上,对收发探头间特定路径的平均声衰减的估计可以表示为
| $ \int_{{\rm{ray}}} {\left( {\alpha - {\alpha _0}} \right)} {\rm{d}}l = \frac{1}{{{f_{\rm{c}}}}}\ln \frac{{{A_{\rm{s}}}}}{{{A_{\rm{r}}}}}, $ | (1) |
式中:As是单介质场(全水)时的接收信号,Ar是内含物(油泡)存在时的接收信号,α0表示单介质场的声衰减系数。
超声层析成像的重建过程为:被测场域共包含n个像素,测试数据共构成m条路径,随着第j个像素在第i条路径上位置的确定,像素上的声衰减系数用式(1)进行求解。将其简化为矩阵表示的形式:
| $ \mathit{\boldsymbol{R}} \cdot a = \tau , $ | (2) |
式中:a=aj-a0, (a∈Ωn×1, j=1, …, n)表示场域各像素衰减系数的变化量;
| $ \mathit{\boldsymbol{R}} \cdot a = \tau + {\tau _{{\rm{noise}}}}, $ | (3) |
式中:τnoise表示加性噪声。超声成像图像重建算法需根据预先计算的系数矩阵R和从传感器阵列中得到的边界测量数据τ计算衰减系数分布a。在式(2)和式(3)中,系数矩阵R的计算过程一般称为“正问题求解”过程。本文采用面积占比法[5]对系数矩阵进行求解,系数矩阵中的元素rij为第i条投影路径和第j个像素之间的重叠面积占该像素面积的比例。
2 图像重建算法 2.1 同步代数迭代重建方法在使用传统的反投影方法对式(2)进行逆问题求解时,往往将矩阵R-1等效成RT进行重建计算,这一方法严重影响重建的精度。1984年,Anderson和Kak[12]提出同步代数重建(simultaneous algebraic reconstruction technique, SART)的方法,有效融合了ART和SIRT的优点,在保持算法鲁棒性的基础上可大幅提升成像质量和算法收敛速度,其迭代过程表示为
| $ \begin{array}{l} a_j^{\left( {k + 1} \right)} = \mathit{\boldsymbol{P}}\left[ {a_j^{(k)} + \frac{\lambda }{{\sum\nolimits_{i = 1}^m {{r_{ij}}} }} \cdot } \right.\\ \left. {\sum\limits_{i = 1}^m {\frac{{{r_{ij}}\left( {{\tau _i} - \sum\nolimits_{j = 1}^n {{r_{ij}}} a_j^{\left( k \right)}} \right)}}{{\sum\nolimits_{j = 1}^n {{r_{ij}}} }}} } \right], \end{array} $ | (4) |
式中:rij代表系数矩阵R中的元素;aj表示第j个像素的声衰减系数;τi表示第i条路径的信号衰减;λ表示迭代过程中的松弛因子;P为高通滤波器模板,表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}} = \int_x {\int_y {\left[ {\delta \left( {x - {x_i},y - {y_i}} \right) - } \right.} } }\\ {\left. {\frac{{\rm{ \mathsf{ π} }}}{{{w^2}}}{{\rm{e}}^{ - \left( {{{\rm{ \mathsf{ π} }}^2}/{w^2}} \right)\left( {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}} \right)}}} \right]{\rm{d}}x{\rm{d}}y,} \end{array} $ | (5) |
式中:δ(x-xi, y-yi)代表二维狄拉克函数,w为频率系数,(x, y)表示滤波器模板中像素坐标,(xi, yi)表示滤波器模板目标像素的坐标。将SART的迭代过程转化成矩阵形式,表示为
| $ {\mathit{\boldsymbol{a}}^{(k + 1)}} = {\mathit{\boldsymbol{a}}^{(k)}} + \lambda {S_{\rm{p}}}{\left( {{S_{\rm{r}}}\mathit{\boldsymbol{R}}} \right)^{\rm{T}}}\left( {\tau - \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{a}}^{(k)}}} \right), $ | (6) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_{\rm{p}}} = diag\left( {1/{R_{ + ,1}},1/{R_{ + ,2}}, \cdots ,1/{R_{ + ,n}}} \right)}\\ {{S_{\rm{r}}} = diag\left( {1/{R_{1, + }},1/{R_{2, + }}, \cdots ,1/{R_{m, + }}} \right)} \end{array}} \right., $ | (7) |
式中:
SART算法在迭代过程中,计算速度受每步运算中的矩阵维度影响较大。为提升算法速度以满足成像实时性要求,需要对SART算法中系数矩阵的维度进行压缩。根据系数矩阵的构建方式及其稀疏性特点,选取截断奇异值分解(truncated singular value decomposition,TSVD)方法对系数矩阵R进行降维处理,进而提升重建算法速度以满足实时性要求。
TSVD作为一种常见的特征提取方法,广泛用于主成分分析及大型复杂系统识别,其数学基础为奇异值分解(singular value decomposition, SVD)。对于给定的系数矩阵R,其奇异值分解形式表示为
| $ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}, $ | (8) |
式中:U∈Ωm×m为右奇异正交向量; V∈Ωn×n为右奇异特征向量;Σ∈Ωm×n为半正定的对角矩阵,其对角元素为矩阵R的奇异值。矩阵U和矩阵V中的每一列分别表示为ui, (i=1, …, m)和vi, (i=1, …, m),利用正交投影算子,可以将系数矩阵和其原解投影到低维子空间中,有效减小系统的维数。选用矩阵V的子空间Vq作为正交投影算子,其计算方式为
| $ {V_q} = span\left\{ {{v_1},{v_2}, \cdots ,{v_q}} \right\}. $ | (9) |
式中:q表示截断系数,{v1, v2, …, vq}为矩阵R最大的q个奇异值对应的矩阵V中的列。令Vq=V, 得到TSVD的基本形式为
| $ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}} \approx {\mathit{\boldsymbol{U}}_q}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_q}\mathit{\boldsymbol{V}}_q^{\rm{T}}. $ | (10) |
在对系数矩阵R进行截断的同时,需要给出SART每步迭代计算的TSVD形式。首先在子空间中,对a进行降维处理:
| $ \mathit{\boldsymbol{\hat a}} = \mathit{\boldsymbol{V}}_q^{\rm{T}}\mathit{\boldsymbol{a}}, $ | (11) |
将式(10)、式(11)代入式(4)并将V替换成Vq,可以得到
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_q}{{\mathit{\boldsymbol{\hat a}}}^{(k + 1)}} = \mathit{\boldsymbol{\hat P}}\left[ {{\mathit{\boldsymbol{V}}_q}{{\mathit{\boldsymbol{\hat a}}}^{(k)}} + \alpha {\mathit{\boldsymbol{S}}_q} \cdot } \right.}\\ {\left. {{\mathit{\boldsymbol{V}}_q}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_q^{\rm{T}}\mathit{\boldsymbol{U}}_q^{\rm{T}}\mathit{\boldsymbol{S}}_r^{\rm{T}}\left( {\tau - {\mathit{\boldsymbol{U}}_q}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_q}{{\mathit{\boldsymbol{\hat a}}}^{(k)}}} \right)} \right],} \end{array} $ | (12) |
令
| $ {{\mathit{\boldsymbol{\hat a}}}^{(k + 1)}} = \mathit{\boldsymbol{\hat P}}\left[ {{{\mathit{\boldsymbol{\hat a}}}^{(k)}} + \alpha {{\mathit{\boldsymbol{\hat S}}}_q}{{\mathit{\boldsymbol{\hat G}}}_q}\mathit{\boldsymbol{S}}_r^{\rm{T}}\left( {\tau - {\mathit{\boldsymbol{G}}_q} \cdot {{\mathit{\boldsymbol{\hat a}}}^{(k)}}} \right)} \right], $ | (13) |
式中:Gq是正交变换后的系数矩阵,Uq和Σq分别是变换后的矩阵U和矩阵S。
对于涉及滤波的SART算法而言,滤波器模板P同样也需要进行降维处理,对应低维的迭代算法表示为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat a}}}_{f\left( {k + 1} \right)}} = \mathit{\boldsymbol{V}}_q^{\rm{T}}{\mathit{\boldsymbol{a}}_{f\left( {k + 1} \right)}} = \\ \mathit{\boldsymbol{V}}_q^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{V}}_q}\left( {{{\mathit{\boldsymbol{\hat a}}}_{{s^{(k + 1)}}}} + \alpha {{\mathit{\boldsymbol{\hat S}}}_q}\mathit{\boldsymbol{G}}_q^{\rm{T}}\mathit{\boldsymbol{S}}_q^{\rm{T}}\left( {\tau - {\mathit{\boldsymbol{G}}_q}{{\mathit{\boldsymbol{\hat a}}}_{{s^{(k + 1)}}}}} \right)} \right). \end{array} $ | (14) |
为提升图像重建精度及分辨率,在采用基于TSVD的SART算法实现图像初步重建的基础上,进一步采用高斯回归模型(Gaussian process regression,GPR)对低分辨率重建结果进行处理,实现高分辨率重建图像。
GPR是一种实现各种统计学习问题的常用工具,它通过对训练数据样本,获得输入输出间的联合概率分布和预测数据的先验概率分布,并计算预测数据输出的后验概率分布。与卷积神经网络(convolutional neural network,CNN)相比,GPR的训练集与测试集的输入数据不必保证数据维度一致。与线性回归为代表的拟合方法相比,GPR可以有效减少局部测试集输入数据误差所引入的波动,对训练样本中的噪声和扰动有较好的鲁棒性[13]。因此,本文中采用GPR将迭代求解的低分辨率重建结果映射到高分辨率重建图像,在保持成像主体对象高分辨率重建的同时,将重建结果中的伪影和图像噪声在映射过程中有效去除,提升图像纯净度。
给定训练集D{(xi, yi), i=1, …n}={X, y},其中X表示低分辨率重建结果各个节点坐标,y表示各个节点重建的衰减系数值。假定xi至yi的映射f(xi)符合正态分布,则x至y的映射可以表示成为高斯过程(Gaussian process),其概率分布表示为
| $ \left\{ \begin{array}{l} f(x) \sim N\left( {m(x),\mathit{\boldsymbol{k}}\left( {x,{x^\prime }} \right)} \right)\\ \;\;\;\;m(x) = E[f(x)]\\ k\left( {x,{x^\prime }} \right) = E\left[ {(f(x) - m(x))\left( {f\left( {{x^\prime }} \right) - m\left( {{x^\prime }} \right)} \right)} \right] \end{array} \right., $ | (15) |
式中:m(x)表示均值,k(x, x′)表示协方差矩阵。设数据集中要预测的数据输入为X*,输出为f*,则根据贝叶斯公式
| $ p\left( {{f_*}|f} \right) = \frac{{p\left( {f|{f_*}} \right)p\left( {{f_*}} \right)}}{{p(f)}} = \frac{{p\left( {f,{f_*}} \right)}}{{p(f)}}. $ | (16) |
GPR的核心是根据训练数据的概率分布和训练及预测数据的联合概率分布,计算预测数据输出的后验概率分布。训练数据的概率分布p(f)由式(15)给出,训练数据与预测数据的联合概率分布为
| $ \left[ {\begin{array}{*{20}{c}} y\\ {{f_*}} \end{array}} \right] \sim N\left\{ {0,\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}(X,X)}&{\mathit{\boldsymbol{K}}\left( {X,{X_*}} \right)}\\ {\mathit{\boldsymbol{K}}\left( {{X_*},X} \right)}&{\mathit{\boldsymbol{K}}\left( {{X_*},{X_*}} \right)} \end{array}} \right]} \right\}, $ | (17) |
式中:K(X*, X)为半正定的协方差矩阵。根据式(15)、式(17),预测数据输出的联合后验概率分布为
| $ \left\{ \begin{array}{l} {f_*}\left| {X,y,{X_*}} \right. \sim N\left\{ {{m_*},cov\left( {{f_*}} \right)} \right\}\\ {m_*} = \mathit{\boldsymbol{K}}\left( {{X_*},X} \right){\left[ {\mathit{\boldsymbol{K}}\left( {X,X} \right)} \right]^{ - 1}}y\\ cov\left( {{f_*}} \right) = \mathit{\boldsymbol{K}}\left( {{X_*},{X_*}} \right) - \\ \mathit{\boldsymbol{K}}\left( {{X_*},X} \right){[\mathit{\boldsymbol{K}}(X,X)]^{ - 1}}\mathit{\boldsymbol{K}}\left( {X,{X_*}} \right) \end{array} \right., $ | (18) |
对于半正定协方差矩阵的选取,考虑到训练数据于测试数据的输入均为坐标值,具有数值上的周期性和范数上的单调性。因此选用平方指数协方差函数作为高斯回归模型的核函数,其计算方式为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{SE}}\left( {{x_i},{x_j}} \right) = \sigma _f^2\exp \left[ { - \frac{1}{2}{{\left( {{x_i} - {x_j}} \right)}^{\rm{T}}}{Q^{ - 1}}\left( {{x_i} - {x_j}} \right)} \right]}\\ {Q = diag\left( {{l_1} \cdots {l_m}} \right)} \end{array}} \right., $ | (19) |
高斯回归预测高分辨率成像结果的具体实现步骤为:
1) 使用前述降维SART方法获得低分辨率成像结果(X, y),其中X表示低分辨率成像结果各像素坐标,y表示低分辨率成像结果像素值。
2) 基于选定的核函数,根据式(15)计算高斯回归模型参数。
3) 基于高分辨率图像各像素点坐标X*,根据式(18)计算高分辨率像素的概率密度分布f*,并求得各像素取值y*。
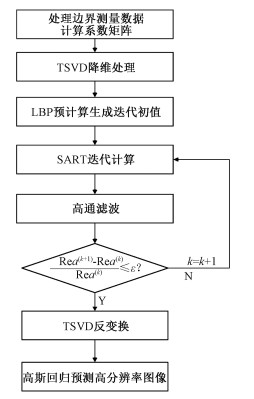
采用高斯回归预测的超声层析成像图像重建算法(SART-GPR)流程图如图 2所示。算法中,首先对边界测量数据进行处理并根据面积占比法进行系数矩阵R的计算;然后使用TSVD降维并基于SART算法进行迭代计算;当残差小于设定阈值时,通过GPR进行预测并给出最终的高分辨率成像结果。
3 仿真结果和讨论 3.1 仿真设置为验证算法在成像精度、计算速度方面的优势,采用仿真实验的方法验证对不同情况下的内含物结构进行成像测试。仿真实验的数值计算通过COMSOL多物理场仿真软件实现,以使其具有强大的偏微分波动方程求解能力和最优解迭代快速收敛的优点。
|
Download:
|
| 图 2 高斯回归预测重建算法流程 Fig. 2 Flow chart of the proposed reconstruction method | |
边界测试数据求解过程中,场域边界的声压分布由狄利克雷方程控制,物理场的控制方程为基于动量守恒和质量守恒的等熵二维波动方程为
| $ \nabla \left( {\frac{1}{{{\rho _0}}}{\nabla _{{p^\prime }}}} \right) - \frac{1}{{{\rho _0}{c^2}}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} = 0, $ | (20) |
式中:ρ0为背景介质的密度,p为质点的声压分布,c代表质点处的声速。
使用有限元法对超声传播过程进行数值计算的过程中,场域内网格剖分的尺寸为波长的1/6,保证在计算精度的同时尽可能减小计算资源的占用。仿真计算的相关参数设置详见表 1。
|
|
表 1 仿真参数设置 Table 1 Simulation parameter setting |
在采用仿真测试数据的重建中,采用在超声层析成像中广泛应用的图像重建算法与本文所提出的SART-GPR方法进行比较(其他算法使用线性插值将分辨率提升到与SART-GPR相同的水平)。为定量比较分析重建效果,定义相对误差和相关系数两个重建指标:
| $ {\rm{RE}} = \frac{{{{\left\| {\sigma - {\sigma ^*}} \right\|}_2}}}{{{{\left\| {{\sigma ^*}} \right\|}_2}}}. $ | (21) |
| $ {\rm{CC}} = \frac{{\sum\limits_{j = 1}^N {\left( {{\sigma _j} - \bar \sigma } \right)} \left( {\sigma _j^* - {{\bar \sigma }^*}} \right)}}{{\sqrt {\sum\limits_{j = 1}^N {{{\left( {{\sigma _j} - \bar \sigma } \right)}^2}} \sum\limits_{j = 1}^N {{{\left( {\sigma _j^* - {{\bar \sigma }^*}} \right)}^2}} } }}. $ | (22) |
式中:σ表示重建的衰减系数分布,σ*表示真实的衰减系数分布,σ和σ*分别表示σ和σ*的平均值。
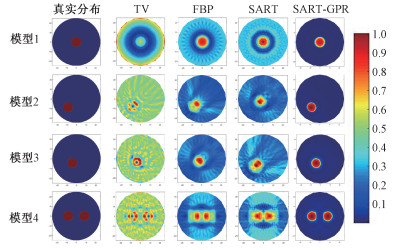
3.2 成像结果图 3给出TV、FBP、未经优化的SART与本文提出的SART-GPR算法的单内含物和双内含物分布成像结果,所有成像结果经归一化处理以便比较。从图中可以看出,传统的TV、FBP及未经优化的SART算法成像结果伪影均较严重,图像纯净度低;SART-GPR算法的成像结果几乎无伪影,且图像纯净度相比其他算法有显著的提升。
|
Download:
|
| 图 3 不同算法重建结果 Fig. 3 Reconstruction results using different methods | |
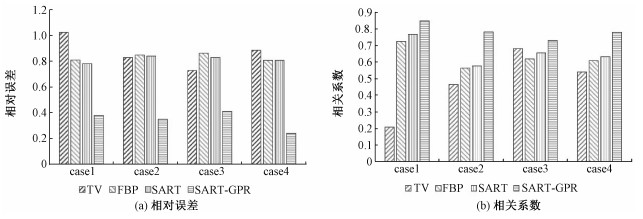
进一步根据式(21)、式(22)计算成像结果的相关系数和相对误差,结果如图 4所示。图 4中,SART-GPR算法的平均相对误差减小至其他3种算法的1/2以下,达到25.3%;平均相关系数与其他3种算法相比也有所提升,达到88.6%。
|
Download:
|
| 图 4 图像重建定量指标对比 Fig. 4 Quantitative comparison of image reconstruction | |
SART-GPR算法的成像结果受投影数量(即探头数目)影响,随着探头数量的增加,成像结果的边缘梯度(保边性)及内含物尺寸的重建精度均有明显提高。针对图 3中的模型1至模型4,SART-GPR算法在采用16、32、48和64探头时,成像的平均相对误差分别为0.427、0.253、0.204和0.181;平均相关系数分别为0.635、0.886、0.907和0.914。
3.3 成像速度针对用于油水两相流流动过程成像的实时性要求,为提升算法的计算速度,使用TSVD对系数矩阵R及SART算法过程进行降维处理,其中截断系数q的选取对重建结果有着较大影响。较大的截断系数可以保留系数矩阵中的主要奇异值,重建精度相对较高,但矩阵维度较大,重建过程较为耗时;较小的截断系数可以减小矩阵维度、加快计算速度,但其重建精度将有明显下降。
图 5为不同截断参数q下的图像重建结果的相对误差和计算时间曲线。为分析不同探头数目对成像结果的影响,分别采用16、32、48和64共4组超声换能器数目进行图像重建。图中,所计算的定量评估指标为图 3中的模型1至模型4计算结果的平均值。
图 5中,随着探头数目增加,重建精度会明显提高,但相应计算时间也会增加。因此在实际测试时需要根据测试目标的要求和测试实时性要求合理选择探头数量。此外,在确定探头数目下,随着截断系数p的增大,重建误差明显减小,计算时间显著增大;当截断系数较小时,重建误差较高,而计算时间较短。为平衡计算时间与重建误差之间的矛盾关系,采用L-曲线法[14]对截断参数q进行优化,L曲线分布及优化结果如图 6所示。经优化,截断参数q选取为0.4,相应的不同算法计算时间对比如表 2所示。

|
Download:
|
| 图 5 不同截断参数下误差及时间 Fig. 5 Errors and speeds at different truncation parameter values | |

|
Download:
|
| 图 6 L曲线分析结果 Fig. 6 Results of L-curve analysis | |
|
|
表 2 不同算法成像时间对比 Table 2 Computing time comparison among different methodss |
表 2中,FBP算法成像速度最快,TV次之,传统SART算法成像速度较慢,不能做到实时在线成像。SART-GPR算法的成像速度相比传统SART算法提升约9倍,其成像速率达到35幅/s,可以满足实时成像需求。
4 总结针对采用阵列式超声传感器实现以油水两相流为代表的弱声阻抗比两相介质分布重建问题,提出一种基于高斯回归预测的高分辨率相介质分布图像重建方法。在获取采用超声连续波激励的方式的边界测量数据基础上,提取边界测量声压幅值的衰减信息。在逆问题成像算法方面,通过采用能够同时兼顾重建速度和重建精度的基于截断奇异值分解的同步代数迭代重建算法,并通过构建高斯回归模型,将低分辨率重建结果转化为高分辨率图像。
通过对仿真模型测试数据的分析,所提出的算法成像精度及图像纯净度相比传统方法明显提高,算法平均相对误差减小至25.3%,平均相关系数提升至88.6%。经TSVD降低维度后,算法成像速率达到35幅/s,满足实时成像需求。
未来工作需要在构建超声信号激励与采集系统,对所提出的算法进行实验验证;并进一步探索超声层析成像技术实现油水两相流介质分布高效重建的方法。
| [1] |
李永明, 苏明旭, 袁安利, 等. 基于超声的管道内粉体体积分数的测量[J]. 中国科学院大学学报, 2016, 33(2): 277-282. |
| [2] |
谭超, 董峰. 多相流过程参数检测技术综述[J]. 自动化学报, 2013(11): 1923-1932. |
| [3] |
郭烈锦. 21世纪多相流热物理学科的未来与挑战[J]. 科技导报, 1995, 10: 8-9. |
| [4] |
王智博, 张骏, 李拓, 等. 基于已知振幅信息约束的叠层光电成像[J]. 中国科学院大学学报, 2017, 34(5): 543-550. |
| [5] |
Rahiman M H F, Rahim R A, Rahim H A. An investigation on chemical bubble column using ultrasonic tomography for imaging of gas profiles[J]. Sensors and Actuators, 2014, 202: 46-52. Doi:10.1016/j.snb.2014.05.043 |
| [6] |
Bieberle M, Bartherl F, Hampel U. Ultrafast X-ray computed tomography for the analysis of gas-solid fluidized besds[J]. Chemical Engineering Journal, 2012, 189/190: 356-363. Doi:10.1016/j.cej.2012.02.028 |
| [7] |
Xu L J, Xu L A. Gas/liquid two-phase flow regime identification by ultrasonic tomography[J]. Flow Measurement and Instrumentation, 1997, 8(3): 145-155. |
| [8] |
Chiew L G, Abdul R R, Fazalul R H. Simulative and experimental studies:void fraction detection in a bubble column of a conducting pipe[J]. IEEE Transactions on Industrial Electronics, 2017, 64: 9636-9645. Doi:10.1109/TIE.2017.2711537 |
| [9] |
Song X Z, Xu Y B, Dong F. A spatially adaptive total variation regularization method for electrical resistance tomography[J]. Measurement Science and Technology, 2015, 26: 125401. Doi:10.1088/0957-0233/26/12/125401 |
| [10] |
Tepe J, Schuster T, Littau B. A modified algebraic reconstruction technique taking refraction into account with an application in terahertz tomography[J]. Inverse Problems in Science and Engineering, 2017, 25(10): 1448-1473. Doi:10.1080/17415977.2016.1267168 |
| [11] |
Cardenas D A C, Furuie S S. Improving priors for USTC via transmission tomography: a simulation study[C]//World Congress on Medical Physics and Biomedical Engineering, Prague, Czech. 2018, 1: 177-181.
|
| [12] |
Andersen A, Kak A C. Simultaneously algebraic reconstruction technique (SART):a super implementation of the ART algorithm[J]. Ultrasound Imaging, 1984, 3: 81-94. Doi:10.1016/0161-7346(84)90008-7 |
| [13] |
Li J M, Qu Y Y, Li C H, et al. Learning local Gaussian process regression for image super-resolution[J]. Neurocomputing, 215, 154: 284-295.
|
| [14] |
Pei Y, Xu Y B, Dong F. A modified L-curve method for choosing regularization parameter in electrical resistance tomography[C]//IEEE International Conference on Imaging System and Techniques (IST), Macau, China, 2015: 55-60.
|
 2020, Vol. 37
2020, Vol. 37 


