2. 蒙纳士大学化学工程学院 ARC计算颗粒技术研究中心, 克莱顿, Vic 3800, 澳大利亚
2. ARC Research Hub for Computational Particle Technology, Department of Chemical Engineering, Monash University, Clayton, Vic 3800, Australia
加压煤分级转化技术改变了长期以来煤炭资源直接燃烧、气化、液化等传统利用方式[1],有机结合煤热解与燃烧发电、煤气利用、煤焦油加工利用等多个过程,将煤炭中的不同成分,如煤气、焦油和半焦分离出来分级利用,可以有效提高煤炭的利用效率和环境效益[2-4]。煤快速热解是该技术的关键,也是加氢、燃烧和气化过程的初始和伴随反应,可获得煤气、焦油等高附加值产品,且热解后生成的半焦得到了有效净化,可用于燃烧发电或作为热解过程的热载体[5]。
加压喷动流化床兼具固定床、流化床和喷动床等反应器的优势,并可有效提高煤热解过程各产物的收率和质量[6]。作为煤快速热解过程的反应器,其开发设计对加压煤分级转化技术的研究至关重要。由于实验成本高及测量手段复杂等因素,采用实验方法研究具有相当大的局限性。数值模拟方法是研究复杂稠密气固系统中气固两相流的重要手段,能够有效弥补现有实验条件与测试手段的不足,形象再现流动场景,反映流场细节。在气固反应系统中,采用合理的数理模型通过数值模拟,可以同时获得系统内温度、速度、组分分布等反应特性,不仅可用于反应器的设计开发,同时可作为实验手段的辅助,对反应器内部的流动和反应特性进行研究。
为设计开发中试规模的加压喷动流化床煤热解反应器,本文进行了处理量为50 kg/h的中试尺度喷动流化床反应器内加压煤快速热解过程的数值模拟。其中,气相场采用欧拉方法,固相场采用基于拉格朗日坐标体系的离散颗粒模拟方法,挥发分析出模型由实验确定。基于数值实验,开展了不同反应器高度、煤进料口位置等结构参数以及不同压力(0.1、0.3和0.5 MPa)、射流风与流化风比值(0.2、0.3和0.4)和粒径(0~3和0~6 mm)等操作参数的影响规律研究,以期为加压煤快速热解过程的反应器开发设计提供指导。
1 数理模型 1.1 数值方法采用基于多相流质点网格法(MP-PIC)建立加压煤快速热解气固流动与化学反应耦合的数理模型,气相场采用基于欧拉坐标体系的大涡模拟(LES)湍流模型,固相场采用基于拉格朗日坐标体系的离散颗粒模拟方法,主要控制方程[7-8]如下:
1) 气相控制方程
气相场连续性方程为
| $ \frac{{\partial \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{\mathit{\boldsymbol{u}}_{\rm{g}}}} \right) = \delta \;{{\dot m}_{\rm{s}}}, $ | (1) |
式中:ug, αg, ρg分别为气体速度矢量、体积分数和密度;
气相场动量方程为
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{\mathit{\boldsymbol{u}}_{\rm{g}}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{\mathit{\boldsymbol{u}}_{\rm{g}}}{\mathit{\boldsymbol{u}}_{\rm{g}}}} \right) = }\\ { - {\alpha _{\rm{g}}}{\nabla _p} + F + {\alpha _{\rm{g}}}{\rho _{\rm{g}}}g + \nabla \cdot \left( {{\alpha _{\rm{g}}}{\tau _{\rm{g}}}} \right), } \end{array} $ | (2) |
式中:p为平均压力, τg为气体应力张量,g为重力加速度,F为气固间的动量交换率。
气相场能量方程为
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{h_{\rm{g}}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{h_{\rm{g}}}{\mathit{\boldsymbol{u}}_{\rm{g}}}} \right) = }\\ {{\alpha _g}\left( {\frac{{\partial p}}{{\partial t}} + {\mu _{\rm{g}}} \cdot \nabla p} \right) + \varphi - \nabla \cdot \left( {{\alpha _{\rm{g}}}q} \right) + \dot Q + {S_{\rm{h}}} + {{\dot q}_{\rm{D}}}, } \end{array} $ | (3) |
式中:hg为气体的焓:φ为黏性耗散;
组分输运方程为
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{Y_{{\rm{g}}i}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _{\rm{g}}}{\rho _{\rm{g}}}{Y_{{\rm{g}}i}}{u_{\rm{g}}}} \right) = }\\ {\nabla \cdot \left( {{\rho _{\rm{g}}}{D_{\rm{g}}}{\alpha _{\rm{g}}}\nabla {Y_{{\rm{g}}i}}} \right) + \delta \;{{\dot m}_{i, {\rm{ chem}}}}, } \end{array} $ | (4) |
式中,
2) 颗粒相控制方程
在MP-PIC方法中,颗粒相的运动通过求解颗粒分布函数f得到,f的输运方程为
| $ \frac{{\partial f}}{{\partial t}} + \frac{{\partial \left( {f{\mathit{\boldsymbol{u}}_s}} \right)}}{{\partial x}} + \frac{{\partial (f\mathit{\boldsymbol{A}})}}{{\partial {\mathit{\boldsymbol{u}}_s}}} = {\left( {\frac{{\partial f}}{{\partial t}}} \right)_{{\rm{coll }}}}, $ | (5) |
颗粒运动方程为
| $ \mathit{\boldsymbol{A}} = \frac{{{\rm{d}}{\mathit{\boldsymbol{u}}_s}}}{{{\rm{d}}t}} = \beta \left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{\rm{s}}}} \right) - \frac{1}{{{\rho _{\rm{s}}}}}\nabla p - \frac{1}{{{\alpha _{\rm{s}}}{\rho _{\rm{s}}}}}\nabla {\tau _{\rm{s}}} + g + {F_{\rm{s}}}. $ | (6) |
式中:τs为颗粒碰撞应力,Fs为颗粒间摩擦力。在MP-PIC方法中,采用颗粒相压力梯度力表征颗粒碰撞,其值随颗粒体积分数单调递增。本模型中,颗粒正应力通过颗粒体积分数计算,由离散颗粒体积插值到网格单元计算,再应用到离散颗粒[8]。颗粒碰撞应力τs的表达式为
| $ {\tau _{\rm{s}}} = \frac{{{P_{\rm{s}}}{\alpha _{\rm{s}}}}}{{{\rm{max}}\left[ {\left( {{\alpha _{{\rm{cp}}}} - {\alpha _{\rm{s}}}} \right), \delta \left( {1 - {\alpha _{\rm{s}}}} \right)} \right]}}, $ | (7) |
式中:αcp为最大堆积密度;Ps为带有压力单位的常数,本文取100 Pa。
3) 煤热解模型
煤热解动力学模型采用单方程模型,假定热解过程在整个颗粒中均匀发生,且煤受热而后分解为煤气、水、焦油和半焦[9],具体表达式如下
Coal → H2O, CO, CO2, H2, CH4, 焦油, 半焦(s).
挥发分的析出速率为
| $ \frac{{{\rm{d}}{V_i}}}{{{\rm{d}}t}} = A{\rm{exp}}\left( {\frac{{ - E}}{{RT}}} \right)\left( {{V_0} - {V_i}} \right), $ | (8) |
式中:Vi和V0分别为i时刻和初始燃烧中的挥发分含量;R为气体常数,8.314×103 J/(kmol·K);T为煤颗粒反应温度; 不同压力下指前因子A与反应活化能E的取值均由煤热解动力学实验获得,详见表 1。
|
|
表 1 不同压力条件下指前因子A与反应活化能E的值 Table 1 Values of the pre-exponential factor A and reaction activation energy E under different pressures |
4) 气固流动与化学反应耦合
本文仅考虑煤受热分解反应,属于非均相反应,因此气相与固相之间存在质量、动量、能量和组分转换,气固流动与化学反应耦合通过设置连续性方程、动量方程、能量方程和组分输运方程的源项实现[10]:对均相反应,并不改变混合物的质量和焓,质量只在气相或者颗粒相相内通过组分输运方程中源项传递,总的气相性质基于混合物中各组分的质量分数计算得到。对非均相反应,由于反应涉及气体和颗粒两相,反应的发生伴随着气固两相之间质量、动量和能量的传递。这一过程通过设置气相/颗粒相质量、动量、能量控制方程中的源项实现。同时,反应物和生成物质量的变化必然导致气相和固相中组分浓度的变化,所以组分输运方程中也包括非均相反应引起的质量转换。
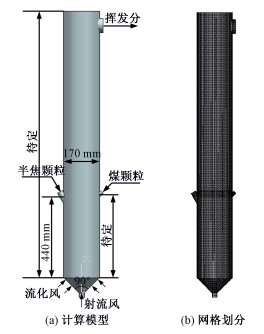
1.2 模拟对象及条件计算模型如图 1(a)所示。该模型为一台初步设计的柱锥体喷动流化床反应器用于煤加压快速热解。反应器直径为200 mm,底部锥角为90°,反应器高度和煤颗粒入口位置由数值模拟进一步确定。采用笛卡尔网格进行划分,分别划分62 767、82 039和103 502共3种网格数量的模型进行网格无关性验证。验证结果表明网格数为82 039的模型兼具计算效率和精度,因此本文选用包含82 039个控制体的模型进行计算,如图 1(b)所示。
|
Download:
|
| 图 1 计算模型及网格划分 Fig. 1 Computational model and grid | |
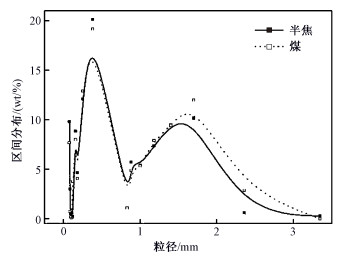
本文中,煤颗粒为反应物,半焦颗粒为热载体,热解气氛为煤气。为简化模型,半焦不参与反应,且忽略热解过程中的二次裂解反应。按照实验条件,热解过程中反应器的温度设置为600 ℃,初始状态时充满氮气。模型中气相场采用速度入口边界条件,并定义煤气组分;煤颗粒和半焦颗粒采用质量流量作为入口边界条件,具体速度值与温度值根据模拟对象设定。计算中出口为压力出口边界,壁面上气相场按无滑移边界处理,壁面与颗粒的碰撞采用反弹(bounce-back)边界条件处理。煤与半焦的两种粒径分布见图 2,模拟采用的煤的工业分析和元素分析见表 2,煤气气氛组分见表 3。其他具体计算参数见表 4,煤与半焦颗粒密度等参数由实验测得,其他参数的选取借鉴文献[9]中的取值。
|
Download:
|
| 图 2 煤热解前后粒径分布图 Fig. 2 Coal particle size distributions before and after pyrolysis | |
|
|
表 2 煤的工业分析和元素分析
Table 2 Proximate analysis and ultimate analysis of coal |
|
|
表 3 模拟煤气组分
Table 3 Coal gas composition in the simulation |
|
|
表 4 模型的计算条件和参数 Table 4 Simulation conditions and parameters |
采用CPFD商业计算软件平台BARRACUDA对本文所建立的模型进行仿真计算。气相场的求解基于SIMPLE算法,采用交错网格定义标量和动量参数,控制方程的离散格式采用有限体积法。对于颗粒相,曳力、重力、压力梯度等参数基于颗粒尺度计算,随后将颗粒体积分数插值到欧拉网格,计算颗粒之间的碰撞正应力,计算结果再插值到离散颗粒。计算热解反应时,将非均相反应插值到欧拉网格计算,再将质量和热量变化等插值回离散颗粒,同时更新气体相和颗粒相的性质[10]。初始时间步长为1×10-4,为提高计算效率,计算软件对时间步长增加Courant-Friedrichs-Lewy(CFL)模块控制。具体求解过程见文献[11-13]。
2 模拟结果与讨论 2.1 典型模拟结果 2.1.1 流型发展图 3为喷动流化床内流型的发展过程,其中压力为0.3 MPa,流化风量0.024 kg/s,射流风量0.007 kg/s(Qs/Qf=0.3)。可以看出,流化风和喷动风进入床层后,在底部入口的锥形布风板上形成射流区和气泡。随后,喷动区域上升,并逐渐通过床层形成喷泉。与此同时,气泡不断上升,并与周围的气泡聚集、增大和破裂,在重力作用下,将颗粒从床层中带出,并落回到床层中,形成稳定的喷流状态。在此过程中,少量颗粒从床面喷出,在密相区上方形成稀相区。极少数小尺寸的颗粒被挥发分从反应器顶部的出口带出。研究指出,喷动流化床中存在至少6种流型状态,如固体床(fixed bed, FB),内部射流(internal jet, IJ),曝气喷动(spouting with aeration, SA),鼓泡射流流化(jet in fluidized bed with bubbling, JFB),腾涌射流流化(jet in fluidized bed with slugging, JFS)以及喷动流化(spouting-fluidizing, SF)等[14-15]。由图可以看出,本文中喷动流化床热解反应器内的流型为鼓泡射流流化,这种状态兼具喷动床和鼓泡流化床的共同特征,是较为理想的流化形态。

|
Download:
|
| 图 3 颗粒体积分数随时间变化图 Fig. 3 Variation in particle volume fraction with time | |
图 4为30 s时压力为0.3 MPa,流化风量0.024 kg/s,射流风量0.007 kg/s(Qs/Qf=0.3)下的热解反应器内挥发分各组分分布图。由于本文的热解模拟采用的流化介质为煤气,因此可以观察到反应器底部的煤气组分,如CO、H2和CH4等浓度较高,均高于稀相区,且前5种组分的分布规律具有相似性。而对于焦油和热解水,由于煤气气氛中不含有这两种组分,因此其分布规律与前5种煤气组分的分布规律不同。在环隙区,半焦与煤颗粒混合均匀,煤热解反应剧烈,大多数挥发分也产生于此。在稀相区,挥发分的分布逐渐均匀,部分煤颗粒还没有热解完全,因此在自由空间区域仍然会有挥发分的析出。

|
Download:
|
| 图 4 挥发分各组分体积分布 Fig. 4 Distributions of volatile components | |
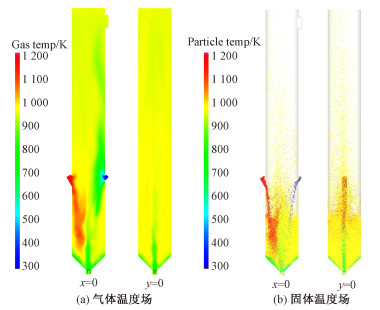
图 5为30 s时反应器内的温度分布。可以看出,煤颗粒入口附近的300 K到床层中央的900 K出现一个明显的温升,而喷动风入口附近的673 K到床表面的1 100 K之间可以观察到另一个温升。在环流区,由于进入反应器原煤为293 K,半焦入口附近的平均温度高于靠近煤的平均温度,但由于半焦和煤颗粒的混合,环流区内的颗粒温度分布较为均匀,高浓度的煤颗粒导致剧烈的热解吸热反应,使该区温度低于半焦入口温度。在反应器下部,裂解反应后的颗粒温度约为873 K。在床层上部可以观察到部分颗粒温度较高,这是由进入反应器高温半焦导致的。密相区的气体温度分布与颗粒温度相似,而稀相区的气体温度分布较为均匀,主要原因是挥发分与流化风或喷动风的均匀混合。
|
Download:
|
| 图 5 反应器内气相与固相温度分布 Fig. 5 Temperature distributions of gas and solid phases in the reactor | |
为选取合适的喷动流化床煤热解反应器的高度,以高度分别为1 500、1 650和1 800 mm的反应器为模型进行加压煤快速热解过程的数值计算。由于反应器高度主要影响稀相区的颗粒分布及顶部出口的颗粒量,因此选取这两个参数对反应器高度进行评估。图 6为同一时刻(30 s)不同高度下反应器内颗粒分布图,其中压力为0.3 MPa,流化风量0.024 kg/s,射流风量0.007 kg/s(Qs/Qf=0.3)。由图可知,虽然受颗粒喷动流化随机性的影响,喷泉高度存在差异,但总体可以看出,当反应器高度为1 500 mm时,稀相区的颗粒分布最为合适,且扬析区刚好未到达顶部挥发分出口。

|
Download:
|
| 图 6 同一时刻不同高度反应器内流型图 Fig. 6 Flow patterns in the reactors having different heights at the same time | |
为评估反应器高度对挥发分出口颗粒量的影响,监测挥发分出口颗粒量。反应器内流型稳定后,3个高度的反应器出口均不再监测到颗粒带出,因此图 7给出至稳定时3种模型下反应器顶部出口总颗粒量。可以看出,随着反应器高度的增加,顶部出口颗粒总量略有减少,但减少的幅度很小,且主要为半焦颗粒。由于稳定后3种反应器出口均不再监测到颗粒,因此无需再过多增加反应器高度,从而增加成本及操作难度。综上,该反应器高度定为1 500 mm最合适。

|
Download:
|
| 图 7 不同高度反应器挥发分出口颗粒量 Fig. 7 Particle outflow at the volatile outlets of the reactors having different heights | |
煤进料口是反应器设计的重要因素,影响着煤颗粒与半焦颗粒的混合程度。而煤与半焦颗粒的混合程度影响反应区的温度分布,进而影响煤热解反应。为选取合适的喷动流化床煤进料口高度,设计并模拟4种不同煤进料口位置的反应器,其同一时刻下煤颗粒与半焦颗粒的分布情况见图 8(a),其中压力为0.3 MPa,流化风量0.024 kg/s,射流风量0.007 kg/s(Qs/Qf=0.3)。可以看出,煤颗粒进料口越高越有利于煤与半焦的混合,这是因为:喷动流化床运行时,气泡的破碎是导致床层表面颗粒剧烈运动的原因,而气泡破碎过程通常发生于床层表面附近。因此,当煤颗粒进料口位于床层表面附近时,进入反应器的煤颗粒刚好可以在床层表面物料剧烈波动的作用下与半焦颗粒加速混合。图 8(b)为同一时刻(30 s)下4种模型的反应器内温度分布。结合图 8(a)、8(b)可以看出,随着煤颗粒进料口位置提高,煤颗粒在反应器某一处大量堆积的现象逐渐减弱,因此颗粒温度也逐渐均匀,这不仅有利于煤颗粒均匀受热充分热解,同时还可防止反应器壁出现受热不均导致颗粒堵塞或反应器外壳材料老化过快。因此,综合上述模拟,煤颗粒进料口位置定为如图所示的距底部470 mm。

|
Download:
|
| 图 8 不同煤进料口位置的反应器内颗粒组分分布和温度分布 Fig. 8 Particle composition distribution and particle temperature distribution in the reactors having different coal inlet positions | |
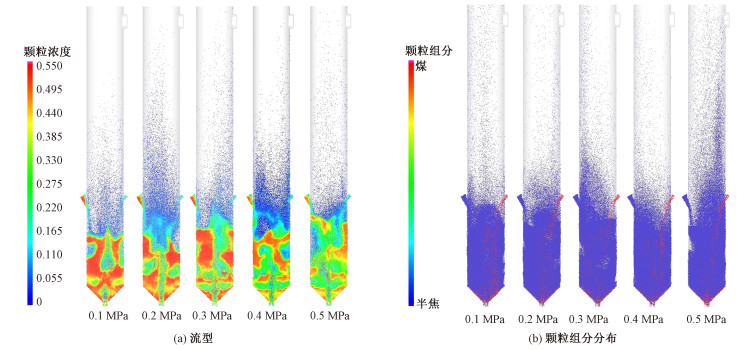
操作压力是加压煤快速热解的重要参数。图 9为流态化条件相同时同一时刻(30 s)不同压力下反应器内流型及煤与半焦的混合状态图。由图 9(a)可知,相同的流态化条件下,压力升高后,反应器内气泡变小且在床层内分布均匀,流型更加稳定。结合图 9(b)可以发现,随着压力升高,反应器内底部出现颗粒堆积的现象。这表明喷动流化床内出现稳定的喷动结构不利于床内煤与半焦的均匀混合,因为稳定的流动结构会在两个物料的落点及其下部区域形成稳定的两个区域,不利于两种物料间的传热,也易造成反应器温度分布不均。该结果与刘雪娇等[16-17]的研究结论一致。该问题可通过调整气速及射流流化风的比值,打乱反应器内流型来解决。
|
Download:
|
| 图 9 不同压力下反应器内流型及颗粒组分分布 Fig. 9 Flow patterns and particle composition distributions in the reactor under different pressures | |
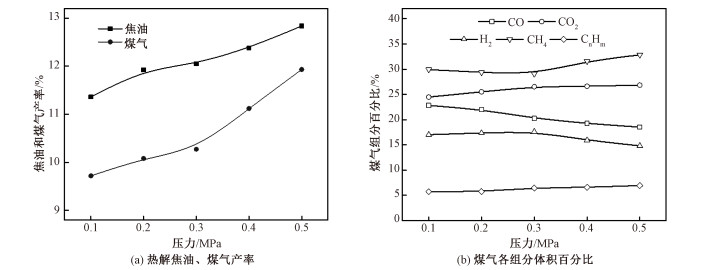
图 10为压力对热解焦油、煤气产率及煤气各组分的影响。煤气气氛下,随热解压力升高,热解焦油产率和煤气产率均提高,其中煤气组分CnHm、CH4、CO2随压力升高体积百分比增加,CO与H2组分体积百分比减少,此现象与窦元元等[18]的实验结果一致。由于该模拟的组分结果已考虑了二次反应的因素,即煤气气氛下,压力升高会促进部分自由基的加氢反应,进而提高焦油产率,同时压力的升高会增加挥发分从煤颗粒析出过程中的阻力,增加其与煤焦的接触时间,相对促进挥发分的二次裂解,造成更多的碳氢化合物析出,提高热解煤气产率。此外,该部分的模拟也从流动的角度揭示了在喷动流化床反应器中压力的升高对热解产生的影响,即提高压力加剧气固流动与颗粒接触,因此为煤颗粒充分热解创造了良好的条件。特别值得注意的是,在本模拟中,由于压力升高降低了煤与半焦的混合程度,一定程度上延长了煤的热解时间,因此压力大于0.3 MPa后,煤气产量上升幅度明显增加。
|
Download:
|
| 图 10 压力对热解焦油、煤气产率及煤气各组分的影响 Fig. 10 Effects of pressure on pyrolysis tar, gas yield, and coal gas components | |
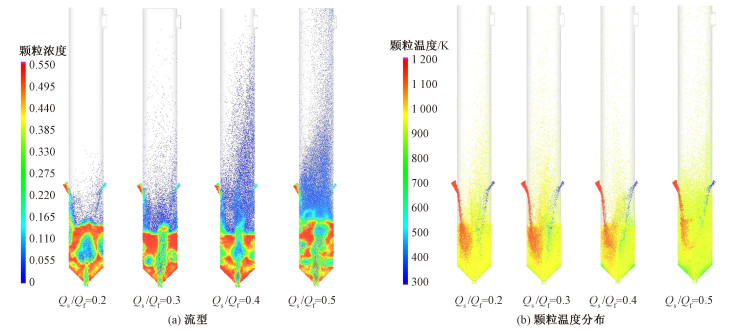
图 11为30 s时流化风量Qf相同,射流风量Qs不同时反应器内流型及颗粒温度分布。可以观察到,当流化风不变,射流风增大时,中心射流现象愈发明显,料层内中心射流区气泡尺寸减小。在床层的中下部, 射流的扰动使射流区和环形区之间颗粒的卷吸、循环和混合加强。反观环形区,由于射流风量增大,难以形成较稳定的气泡。减小射流风的比重后,反应器内流动改变,射流区气泡尺寸增大,但环形区气泡尺寸减小,料面波动减弱。已有的实验研究表明,在射流风和流化风的共同作用下,床层内的物料几乎无法实现完全均匀流化,而是出现如图所示的颗粒与气体在床层中的非均匀分布,而持续增大射流风的最终结果将导致料层波动增强,密相区高度减小,悬浮过渡区高度增加,且稀相区气速和颗粒浓度增加。随着射流风量的增加,反应器内温度分布越来越均匀,这是因为增大射流风量使得床层内颗粒混合扰动增强,从而有助于温度场的均匀分布。
|
Download:
|
| 图 11 不同Qs/Qf下反应器内流型及颗粒温度分布 Fig. 11 Flow patterns and particle temperature distributions in the reactor at different Qs/Qf values | |
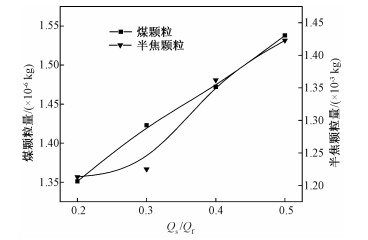
图 12为3种工况下反应器挥发分出口总颗粒量,结合图 11和图 12可以发现,由于射流风量增大,导致稀相区的颗粒量增加,使得部分颗粒随着挥发分由反应器顶部出口带出,导致反应器顶部出口颗粒量增大。这表明实际操作时,射流风量不宜过大,从而给焦油和挥发分的后处理工序增加负担。
|
Download:
|
| 图 12 不同Qs/Qf下反应器挥发分出口颗粒量 Fig. 12 Particle outflow at volatile outlet of the reactor at different Qs/Qf values | |
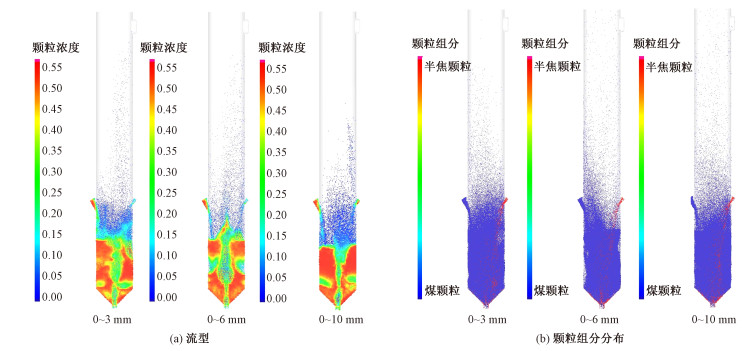
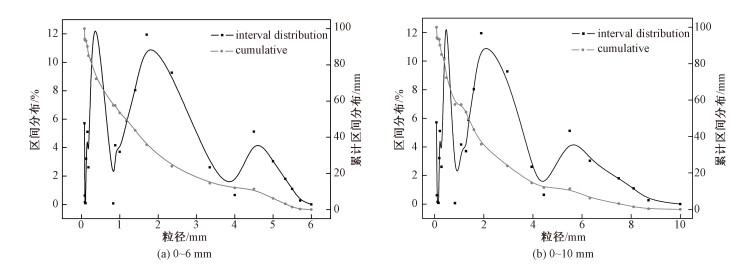
图 13为同一时刻(30 s)下,粒径分布分别为0~3、0~6和0~10 mm时反应器内流型及混合状态。其中,0~6和0~10 mm的粒径分布见图 14。由图 13可知,粒径大小对流型略有影响。总体来说,粒径增大后,反应器内流型更加稳定,床层的形态变得整齐,除中心射流引起的气泡以外,环隙区的气泡更为明显。由反应器内混合图可以发现,粒径分布0~3 mm时,反应器内煤颗粒与半焦颗粒的混合要更加均匀,而粒径分布为0~6 mm时,半焦在反应器底部右侧出现明显的堆积,且这种现象在粒径为0~10 mm时更为严重。原因如2.3.1节所述,这是由于颗粒变细导致床内流型不稳定,从而一定程度上促进了混合,而采用更大的粒径分布时,由于反应器内流型更为稳定,自反应器右侧进入反应器的煤颗粒较难通过颗粒运动进入反应器左边,因此易在反应器右侧堆积。
|
Download:
|
| 图 13 不同粒径范围反应器内流型及颗粒组分分布 Fig. 13 Flow patterns and particle composition distributions in the reactor at different particle sizes | |
|
Download:
|
| 图 14 0~6 mm和0~10 mm粒径分布图 Fig. 14 Particle size distributions between 0 and 6 mm and between 0 and 10 mm | |
表 5为3种工况下反应器挥发分出口总颗粒量,可以发现当粒径范围变大时,由于细颗粒份额减少,导致料层上方的悬浮区以及稀相区的悬浮颗粒减少,因此反应器顶部出口的颗粒量也显著减少。
|
|
表 5 不同粒径范围下反应器挥发分出口颗粒量 Table 5 Particle outflow at volatile outlet of the reactor at different particle sizes |
为设计开发中试规模的加压喷动流化床煤热解反应器,本文进行了处理量为50 kg/h的中试尺度喷动流化床反应器内加压煤快速热解过程的数值模拟。研究反应器高度、煤进料口位置等结构参数以及不同压力(0.1~0.5 MPa)、射流风与流化风比值(0.2~0.5)和粒径(0~3、0~6和0~10 mm)等操作参数的影响规律。研究结论如下:
该热解反应器最合适的高度为1 500 mm,煤进料口越低越不利于煤与半焦的混合传热,煤进料最合适的高度为470 mm;升高压力,煤与半焦混合程度降低,焦油产率提高,煤气产率提高;流化风量Qf不变,随射流风量Qs增加,气固流动更剧烈,颗粒温度分布更加均匀,顶部出口颗量增加;增大粒径虽可降低挥发分出口的颗粒量,但不利于煤与半焦混合。
| [1] |
甘建平, 马宝岐, 尚建选, 等. 煤炭分质转化理念与路线的形成和发展[J]. 煤化工, 2013, 41(1): 3-6. Doi:10.3969/j.issn.1005-9598.2013.01.002 |
| [2] |
甘建平, 马晓迅, 尚建选, 等. 煤炭分质转化利用的节能减排分析[J]. 煤化工, 2011, 39(4): 1-4. Doi:10.3969/j.issn.1005-9598.2011.04.001 |
| [3] |
虞育杰, 姜红丽, 龚德鸿, 等. 低阶煤分级利用技术研究综述[J]. 广东电力, 2018, 31(3): 9-14. |
| [4] |
岑建孟, 方梦祥, 王勤辉, 等. 煤分级利用多联产技术及其发展前景[J]. 化工进展, 2011, 30(1): 88-94. |
| [5] |
吕清刚, 刘琦, 那永洁, 等. 双流化床中煤的热解特性试验研究[J]. 中国电机工程学报, 2010, 30(8): 15-19. |
| [6] |
邓中乙, 肖睿, 金保升, 等. 加压喷动流化床煤气化数值模拟[J]. 燃烧科学与技术, 2009, 15(4): 332-338. Doi:10.3321/j.issn:1006-8740.2009.04.009 |
| [7] |
Snider D, Banerjee S. Heterogeneous gas chemistry in the CPFD Eulerian-Lagrangian numerical scheme (ozone decomposition)[J]. Powder Technology, 2010, 199(1): 100-106. Doi:10.1016/j.powtec.2009.04.023 |
| [8] |
O Rourke P J, Snider D M. An improved collision damping time for MP-PIC calculations of dense particle flows with applications to polydisperse sedimenting beds and colliding particle jets[J]. Chemical Engineering Science, 2010, 65(22): 6014-6028. Doi:10.1016/j.ces.2010.08.032 |
| [9] |
Xie J, Zhong W Q, Jin B S, et al. Eulerian-Lagrangian method for three-dimensional simulation of fluidized bed coal gasification[J]. Advanced Powder Technology, 2013, 24(1): 382-392. |
| [10] |
Zhong W Q, Yu A B, Zhou G W, et al. CFD simulation of dense particulate reaction system:approaches, recent advances and applications[J]. Chemical Engineering Science, 2016, 140(50): 16-43. |
| [11] |
Xie J, Zhong W Q, Jin B S, et al. Eulerian-Lagrangian method for three-dimensional simulation of fluidized bed coal gasification[J]. Advanced Powder Technology, 2013, 24(1): 382-392. Doi:10.1016/j.apt.2012.09.001 |
| [12] |
O'Rourke P J, Snider D M. Inclusion of collisional return-to-isotropy in the MP-PIC method[J]. Chemical Engineering Science, 2012, 80(10): 39-54. |
| [13] |
Loha C, Chattopadhyay H, Chatterjee P K. Three dimensional kinetic modeling of fluidized bed biomass gasification[J]. Chemical Engineering Science, 2014, 109(16): 53-64. |
| [14] |
Shao Y J, Liu X J, Zhong W Q, et al. Recent advances of spout-fluid bed:a review of fundamentals and applications[J]. International Journal of Chemical Reactor Engineering, 2013, 11(1): 243-258. |
| [15] |
Tia S, Bhattacharya S C, Wibulswas P. Combustion behaviour of coal and carbon in spouted and spout-fluid beds[J]. International Journal of Energy Research, 1991, 15(3): 249-255. Doi:10.1002/er.4440150310 |
| [16] |
刘雪娇, 钟文琪, Yu Aibing. 过热蒸汽/热载体/生物质三相混合数值模拟[J]. 工程热物理学报, 2016, 37(5): 1021-1026. |
| [17] |
Liu X J, Zhong W Q, Yu A B, et al. Mixing behaviors in an industrial-scale spout-fluid mixer by 3D CFD-TFM[J]. Powder Technology, 2017, 314: 455-465. Doi:10.1016/j.powtec.2016.10.046 |
| [18] |
窦元元, 钟文琪, 周冠文, 等. 煤加压低温热解制取焦油和煤气特性[J]. 东南大学学报(自然科学版), 2018, 48(1): 85-91. |
 2020, Vol. 37
2020, Vol. 37 


