3D打印能快速制造出传统工艺难以加工的复杂形状实体,是一种极具革命性的数字化生产模式。3D打印技术可以分为熔融沉积成型、光固化快速成型、选择性激光烧结、分层实体制造等[1-3]。熔融沉积成型技术(fused deposition modeling,FDM)作为最常用的3D打印技术之一,由于无需使用激光,直接将成型材料熔化后层层堆积成实体模型,因而具有结构简单、成本低廉、使用便捷等优点[4]。
然而,FDM技术也存在一些缺陷。由于FDM打印机采用低熔点的丝材作为原材料,制得成品的某些机械性能(如强度、韧性等)较差,且材料种类受限,熔点高的塑料无法采用[5]。同时,商业化FDM打印机中丝状材料通常通过摩擦滚轮输送,滚轮对丝材驱动力小,无法大幅提高打印速度。相对于丝状材料,颗粒材料种类丰富、应用广泛,且许多新型材料机械性能完全符合产品要求[6]。螺杆挤出装置能够输运塑料颗粒并使其熔融挤出,且螺杆对颗粒的轴向挤压作用力大[7-8],可有效提高打印速度,故在FDM技术中具有广阔应用前景。
应用于3D打印机进料的螺杆挤出装置中,螺杆结构中颗粒的流动特性影响出口颗粒速度分布及质量流量,并对熔体的流动特性和成品质量产生重要影响。同时,颗粒的材料特性如滚动摩擦系数等直接影响颗粒流动特性。在流化床等设备中,滚动摩擦对颗粒流动特性的影响已得到充分研究,但在螺杆输运结构中,相应研究十分缺乏。
因此,本文针对应用于FDM技术中的螺杆挤出装置,建立颗粒运动和碰撞过程中相应的数学模型,基于离散单元法(discrete element method, DEM)对颗粒流动特性受输运段颗粒与壁面间滚动摩擦的影响进行数值模拟研究,研究颗粒的流动特性包括颗粒速度、质量流量、转矩等。
1 模型建立 1.1 颗粒运动颗粒运动遵循牛顿第二定律。由于装置中各部分压力恒为大气压,且颗粒运动速度小,气相与固相相对运动速度低,故气相对固相颗粒的压力梯度力和曳力作用可以忽略不计[7],颗粒的运动过程只受到周围颗粒对其作用力和自身重力的影响[9-10]:
| $ {m_{\rm{p}}}\frac{{{{\rm{d}}^2}{r_{\rm{p}}}}}{{{\rm{d}}{t^2}}} = \sum\limits_{j = 1}^n {{\mathit{\boldsymbol{F}}_{{\rm{c}}, ij}}} + {m_{\rm{p}}}\mathit{\boldsymbol{g}}, $ | (1) |
式中:mp为颗粒质量(kg);rp为某一颗粒球心位置(m);n为与指定颗粒接触的周围颗粒个数;Fc为接触力(N)。
颗粒转动过程中动量矩定理[11]表示如下
| $ {I_{\rm{p}}}\frac{{{\rm{d}}{\mathit{\boldsymbol{\omega }}_{\rm{p}}}}}{{{\rm{d}}t}} = \sum\limits_{j = 1}^n {\left( {{r_{\rm{p}}} \times {\mathit{\boldsymbol{F}}_{t, ij}} + {\mathit{\boldsymbol{T}}_{{\rm{r}}, ij}}} \right)} , $ | (2) |
式中:Ip为转动惯量(kg·m2);ωp为颗粒角速度(rad/s);Tr为由滚动摩擦产生的颗粒转矩(N·m)。
1.2 颗粒碰撞本研究采用线性弹簧阻尼模型计算颗粒碰撞过程中的接触力。线性弹簧阻尼模型中用弹簧-阻尼器-滑块系统模拟碰撞过程中颗粒间相互作用。其中,弹簧组件表征颗粒间弹性接触力作用,阻尼器表征颗粒间缓冲作用,滑块组件表征颗粒间摩擦滑移等作用[12]。颗粒碰撞过程中接触力表示如下:
| $ {\mathit{\boldsymbol{F}}_{{\rm{c, n}}}} = - {k_{\rm{n}}}{\mathit{\boldsymbol{\delta }}_{\rm{n}}} - {\mathit{\boldsymbol{\eta }}_{\rm{n}}}{\mathit{\boldsymbol{v}}_{{\rm{r, n}}}}, $ | (3) |
| $ {\mathit{\boldsymbol{F}}_{{\rm{c, t}}}} = \left\{ {\begin{array}{*{20}{l}} { - {k_1}{\mathit{\boldsymbol{\delta }}_1} - {\eta _1}{\mathit{\boldsymbol{v}}_{{\rm{r, t}}}}}&{\left( {{\mathit{\boldsymbol{F}}_{\rm{t}}}\left| { \le {\mu _{\rm{f}}}} \right|{\mathit{\boldsymbol{F}}_{\rm{n}}}|} \right)}\\ { - {\mu _{\rm{f}}}\left| {{\mathit{\boldsymbol{F}}_{\rm{n}}}} \right|\frac{{{\mathit{\boldsymbol{v}}_{{\rm{r}}, {\rm{t}}}}}}{{\left| {{\mathit{\boldsymbol{v}}_{\rm{r}}}} \right|}}}&{\left( {\left| {{\mathit{\boldsymbol{F}}_{\rm{t}}}} \right| > {\mu _{\rm{f}}}\left| {{\mathit{\boldsymbol{F}}_{\rm{n}}}} \right|} \right)} \end{array}} \right., $ | (4) |
式中:k为弹簧刚度(N/m);δ为颗粒变形量(m);η为阻尼系数(N·s/m);vr为颗粒相对运动速度(m/s);μf为滑动摩擦系数。
1.3 滚动摩擦颗粒与颗粒、颗粒与壁面间发生碰撞时由于颗粒的转动,相互间存在滚动摩擦作用。滚动摩擦对颗粒的流动特性产生一定影响。为了考虑滚动摩擦的作用,本研究采用一种常见的定向恒转矩模型。该模型假设由滚动摩擦引起的转矩的方向与发生碰撞的颗粒间的相对运动方向总是相反[13]。发生碰撞的颗粒由滚动摩擦引起的转矩表示如下
| $ {\mathit{\boldsymbol{T}}_{\rm{r}}} = - \frac{{{\mathit{\boldsymbol{\omega }}_{ij}}}}{{\left| {{\mathit{\boldsymbol{\omega }}_{ij}}} \right|}}{\mu _{\rm{r}}}{R_{\rm{r}}}\left| {{\mathit{\boldsymbol{F}}_{\rm{n}}}} \right|, $ | (5) |
式中:ωij为颗粒相对旋转角速度(s-1);Rr为相对半径(m),由发生碰撞的颗粒半径确定;μr为无量纲滚动摩擦系数。
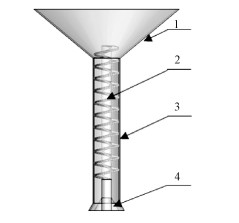
1.4 初始及边界条件图 1为螺杆挤出装置输运段的结构。螺杆装置输运段主要由进料漏斗、螺杆、外管壁及锥形体等结构组成。颗粒由进料漏斗流入,通过转动的螺杆输运到螺杆与锥形体中间的空腔中,并在空腔中堆积。空腔中堆积的颗粒受到转动螺杆对其的作用力,其中向下的轴向分力具有挤压颗粒的作用,并使得颗粒从锥形体与外壁面间的环形间隙中流出。螺杆输运段主要结构参数见表 1。
|
Download:
|
| 1:进料漏斗; 2:螺杆; 3:外管壁; 4:锥形体。 图 1 螺杆挤出装置输运段结构 Fig. 1 Structure of the feeding section | |
|
|
表 1 螺杆挤出装置输运段主要结构参数 Table 1 Main structural parametersof the feeding section |
数值模拟中采用3种不同类型的颗粒:聚乳酸(polylactic acid, PLA),聚丙烯(polypropylene, PP),热塑性聚氨酯(thermoplastic polyurethane, TPU),颗粒直径均为3 mm,模拟时间内流入的颗粒数均为1 000个。螺杆挤出装置所有壁面材料均为钢,密度为7 800 kg/m3,剪切模量为2.07×1011 Pa。模拟中的时间步长基于瑞利时间步确定,设置为4.4×10-7 s。模拟中划分的平均计算网格尺寸为4.5 mm×4.5 mm×4.5 mm,网格总数约为71 136个,通过网格无关性验证证明该尺寸网格已达到网格无关性要求。所有工况的模拟时间均为25 s,并对10~25 s内流动特性参数的取时均值进行研究,因为10 s后空腔内颗粒堆积及流动情况趋于稳定。
基于陈磊[14]及白晓鹏[15]的测量结果,表 2给出3种颗粒材料的主要参数。模拟中PLA、TPU、PP的颗粒间滚动摩擦系数均设定为0.012,针对每种颗粒的颗粒与壁面间滚动摩擦系数分别设置0.012、0.015、0.018、0.021、0.024共5个工况[14, 16-17]。
|
|
表 2 3种颗粒材料主要参数 Table 2 Main material properties forthree kinds of particles |
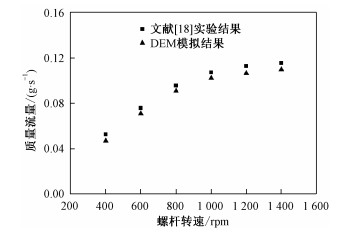
为了验证所选取的模型的准确性,将Roberts和Willis[18]的实验结果与采用本研究中模型的数值模拟结果进行对比。文献[18]实验中采用的是垂直螺旋输送机结构。图 2给出螺旋输送机中螺杆转速不同的各工况下出口颗粒质量流量实验数据与数值模拟结果对比。由图可知,在实验与DEM模拟结果中颗粒质量流量均随螺杆转速的增加而增加,且增加的幅度逐渐减小。不同螺杆转速各工况中DEM模拟结果均比实验结果略低,可能是由于数值模拟中对结构适当简化所致。当螺杆转速为1 200 rpm时。模拟结果与实验结果的相对误差最大,约为5.4%。由此可见,模拟结果与文献[18]实验符合良好,从而验证了所采用模型的合理性。
|
Download:
|
| 图 2 螺旋输送机出口颗粒质量流量实验与模拟结果对比 Fig. 2 Comparison between experiment and simulation results on outlet particle mass flow in the screw conveyer | |
输运段颗粒速度均匀性对螺杆挤出装置挤出成品质量具有重要影响。评判变量分布均匀性的一个重要标准是相对标准偏差(relative standard deviation,RSD):
| $ {\rm{RSD}} = S/\bar V \times 100\% , $ | (6) |
| $ S = \sqrt {\frac{1}{{n - 1}}\sum\limits_{j = 1}^n {{{\left( {{V_j} - \bar V} \right)}^2}} } , $ | (7) |
式中:S为标准偏差(m/s);V为颗粒平均速度(m/s); Vj为挤出的第j个颗粒的速度值(m/s);n为挤出颗粒个数。
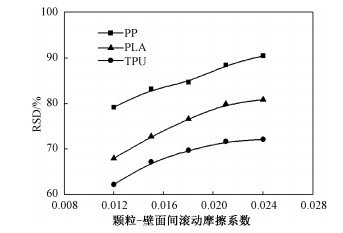
图 3展示颗粒与壁面间滚动摩擦系数对输运段出口处颗粒相对速度标准偏差的影响。随着颗粒与壁面间滚动摩擦系数的增大,3种颗粒在出口处相对速度标准偏差均相应增加,并且增加幅度逐渐减小。这是由于出口处颗粒沿着环向间隙单排流出,颗粒与壁面间滚动摩擦的增大使得与壁面发生碰撞的颗粒速度减小,其与未发生碰撞的颗粒的速度差异增大,导致速度均匀性下降。
|
Download:
|
| 图 3 颗粒与壁面间滚动摩擦系数对相对速度标准偏差的影响 Fig. 3 Effect of rolling friction coefficient between particle and wall on relative standard deviation of velocity | |
当颗粒与壁面间滚动摩擦系数相同时,PP颗粒对应相对速度标准偏差最大,PLA颗粒次之,TPU颗粒最小,说明TPU颗粒在出口处速度更加均匀。当颗粒与壁面间滚动摩擦系数从0.012增至0.024时,PLA颗粒相对速度标准偏差相应从68.0%增至80.8%,增幅最大,达12.8%。由此可知,若想在3D打印进料中使得颗粒出口流动尽可能均匀,应当选择滚动摩擦系数更小、更光滑的颗粒;同时,选择TPU颗粒相比于其余两种颗粒在速度均匀性方面效果最好。
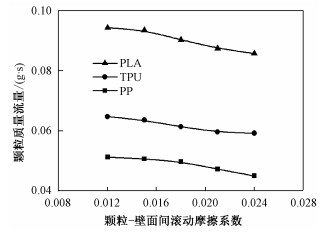
2.2 颗粒质量流量进料段出口颗粒质量流量直接影响3D打印速度。图 4给出各工况下颗粒与壁面间滚动摩擦系数对出口处颗粒质量流量的影响。随着颗粒与壁面间滚动摩擦系数的增大,输运段出口处颗粒的质量流量均近似线性减小,证明颗粒与壁面间滚动摩擦对出口处颗粒流动存在一定的阻碍作用。
|
Download:
|
| 图 4 颗粒与壁面间滚动摩擦系数对出口质量流量的影响 Fig. 4 Effect of rolling friction coefficient between particle and wall on outlet mass flow | |
当颗粒与壁面间滚动摩擦相同时,PLA颗粒对应出口质量流量最高,TPU颗粒次之,PP颗粒对应的出口质量流量最小。当颗粒与壁面间滚动摩擦系数从0.012增至0.024时,PLA颗粒对应的质量流量从0.094 g/s降至0.086 g/s,减少的幅度最大,达8.6%。由此可见,要想在3D打印进料过程中颗粒质量流量更大,可以选择更为光滑的颗粒。
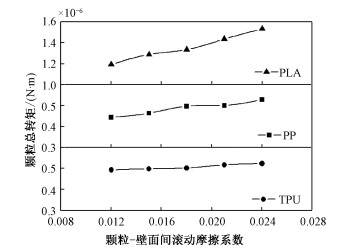
2.3 颗粒转矩颗粒与壁面间的滚动摩擦影响颗粒的转动特性,图 5给出颗粒与壁面滚动摩擦系数对颗粒时均总转矩的影响。随着颗粒与壁面滚动摩擦系数的增加,3种颗粒时均总转矩均随之增加,这是由于颗粒与壁面间滚动摩擦系数的增加使得螺杆壁面对附近颗粒的转动行为的影响增强,周围颗粒获得更大的转矩。
|
Download:
|
| 图 5 颗粒与壁面间滚动摩擦系数对总转矩的影响 Fig. 5 Effect of rolling friction coefficient between particle and wall on total torque | |
当颗粒与壁面间滚动摩擦系数相同时,PP和TPU对应的时均转矩相对较小,PLA颗粒对应的时均转矩最大,其数值为其余两种颗粒转矩的2~3倍。TPU颗粒对应的时均转矩随颗粒与壁面滚动摩擦系数的增加变化很小,说明TPU颗粒受颗粒与壁面间滚动摩擦影响极小。
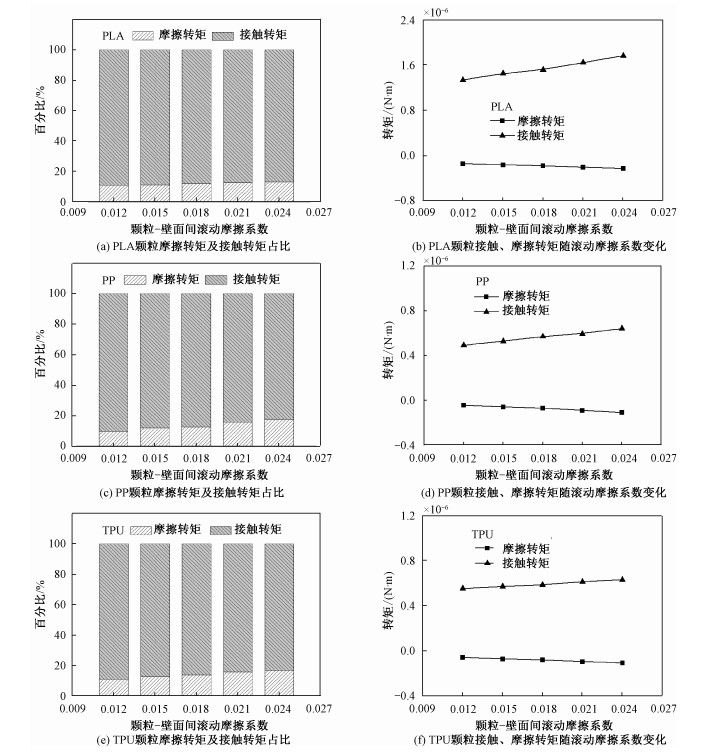
图 6进一步分析颗粒与壁面间滚动摩擦对由摩擦转矩引起的转矩(摩擦转矩)与接触力引起的转矩(接触转矩)的影响规律。图 6(a)、6(c)、6(e)分别给出PLA、PP、TPU颗粒摩擦转矩与接触转矩所占总转矩的百分比。随着颗粒与壁面间滚动摩擦系数的增加,3种颗粒对应的由滚动摩擦引起的转矩占比均略有增加,相应地由接触力引起的转矩占比减小。其中,PLA颗粒摩擦转矩占比受滚动摩擦影响很小,当颗粒与壁面间滚动摩擦系数由0.012增至0.024时,PLA摩擦转矩占比从10.9%增至13.1%,增幅仅2.2%。PP与TPU颗粒对应摩擦转矩占比受滚动摩擦影响较大,且增幅相近,滚动摩擦系数由0.012增至0.024时占比分别增加7.9%和6.5%。
|
Download:
|
| 图 6 颗粒与壁面间滚动摩擦系数对由滚动摩擦及接触力产生转矩的影响 Fig. 6 Effect of rolling friction coefficient between particle and wall on friction and contact torques | |
图 6(b)、6(d)、6(f)则分别展示PLA、PP、TPU颗粒对应的摩擦转矩与接触转矩随颗粒与壁面间滚动摩擦系数的变化。由图可见3种颗粒的摩擦转矩与接触转矩方向始终相反。随着颗粒与壁面间滚动摩擦系数的增加,3种颗粒对应的摩擦转矩与接触转矩均增加,相比而言接触转矩增幅更大,但与图 6(a)、6(c)、6(e)对比可知接触转矩占比反而减小。当颗粒与壁面间滚动摩擦系数从0.012增至0.024时,PLA颗粒对应摩擦转矩与接触转矩绝对值及增幅最大,而PP颗粒对应的摩擦转矩与接触转矩增长比例最快,分别增加149%及30.6%。
3 结论本研究中,针对应用于FDM技术的螺杆挤出装置,基于离散单元法对其输运段中颗粒与壁面间滚动摩擦系数对颗粒流动特性的影响进行数值模拟研究。模拟中分别采用3种类型颗粒(PLA、PP、TPU)。颗粒接触模型采用线性弹簧阻尼模型,并采用针对摩擦转矩的定向恒转矩模型以考虑滚动摩擦的影响。
研究得到的结论如下:随着颗粒与壁面间滚动摩擦系数的增加,3种颗粒的出口质量流量相应减小,同时出口颗粒的速度均匀性相应减小。当颗粒与壁面间滚动摩擦系数从0.012增至0.024时,PLA颗粒对应的质量流量从0.094 g/s降至0.086 g/s,降幅最大,达8.6%;同时相对速度标准偏差由68.0%增至80.8%,增幅最大,达12.8%。3种颗粒总转矩随着颗粒与壁面滚动摩擦系数的增大而增大,工况相同时,PLA颗粒对应的时均转矩最大,PP和TPU对应的时均转矩相对较小。滚动摩擦及接触力引起的转矩随滚动摩擦系数的变化趋势与总转矩均一致,PP颗粒对应的摩擦转矩与接触转矩增幅最大,分别增加149%及30.6%。
在实际应用中,要想在3D打印进料过程中获得更大的质量流量,且出口处颗粒流动更为均匀,最好令颗粒与壁面间滚动摩擦系数更小,即尽量选择更为光滑的颗粒或者使得装置内壁更为光滑。
| [1] |
陈庆来. 3D打印技术在塑料工业中的应用[J]. 塑料科技, 2019, 47(02): 91-94. |
| [2] |
史玉升, 张李超, 白宇, 等. 3D打印技术的发展及其软件实现[J]. 中国科学:信息科学, 2015, 45(2): 197-203. |
| [3] |
张学军, 唐思熠, 肇恒跃, 等. 3D打印技术研究现状和关键技术[J]. 材料工程, 2016, 44(2): 122-125. |
| [4] |
Reddy B V, Reddy N V, Ghosh A. Fused deposition modelling using direct extrusion[J]. Virtual and Physical Prototyping, 2007, 2(1): 51-60. Doi:10.1080/17452750701336486 |
| [5] |
汪甜田. FDM送丝机构的研究与设计[D].武汉: 华中科技大学, 2007. http://d.wanfangdata.com.cn/Thesis/D090957
|
| [6] |
王永双. FDM工艺的实验研究[D].山东青岛: 青岛大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-11065-1015983340.htm
|
| [7] |
Moysey P A, Thompson M R. Modelling the solids inflow and solids conveying of single-screw extruders using the discrete element method[J]. Powder Technology, 2005, 153(2): 95-107. Doi:10.1016/j.powtec.2005.03.001 |
| [8] |
Moysey P A, Thompson M R. Discrete particle simulations of solids compaction and conveying in a single-screw extruder[J]. Polymer Engineering & Science, 2008, 48(1): 62-73. |
| [9] |
Zhou Y C, Wright B D, Yang R Y, et al. Rolling friction in the dynamic simulation of sandpile formation[J]. Physica A:Statistical Mechanics and its Applications, 1999, 269(2-4): 536-553. Doi:10.1016/S0378-4371(99)00183-1 |
| [10] |
耿察民, 钟文琪, 邵应娟, 等. 双循环流化床颗粒分布特性的三维数值模拟[J]. 中国科学院大学学报, 2016, 33(2): 258-264. |
| [11] |
Fukumoto Y, Sakaguchi H, Murakami A. The role of rolling friction in granular packing[J]. Granular Matter, 2013, 15(2): 175-182. Doi:10.1007/s10035-013-0398-8 |
| [12] |
谭骏华, 罗坤, 樊建人. 软球模型在颗粒流全尺度模拟中的验证和分析[J]. 浙江大学学报(工学版), 2015, 49(2): 344-350. |
| [13] |
Ai J, Chen J F, Rotter J M, et al. Assessment of rolling resistance models in discrete element simulations[J]. Powder Technology, 2011, 206(3): 269-282. Doi:10.1016/j.powtec.2010.09.030 |
| [14] |
陈磊.基于数值模拟的塑料颗粒3D打印机关键技术研究[D].哈尔滨: 哈尔滨工业大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10213-1016913853.htm
|
| [15] |
白晓鹏.微孔聚氨酯弹性材料力学性能研究及应用[D].湖南株洲: 湖南工业大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-11535-1015403580.htm
|
| [16] |
Cousseau T, Graça B, Campos A, et al. Friction torque in grease lubricated thrust ball bearings[J]. Tribology International, 2011, 44(5): 523-531. Doi:10.1016/j.triboint.2010.06.013 |
| [17] |
Xu D, Karger-Kocsis J, Schlarb A K. Rolling friction and wear of organoclay-modified thermoplastic polyurethane rubbers against steel[J]. Kautschuk Gummi Kunststoffe, 2008, 61(3): 98. |
| [18] |
Roberts A W, Willis A H. Performance of grain augers[J]. Proceedings of the Institution of Mechanical Engineers, 1962, 176(1): 165-194. Doi:10.1243/PIME_PROC_1962_176_021_02 |
 2020, Vol. 37
2020, Vol. 37 


