2. 复旦大学附属中山医院血管外科, 上海 200032
2. Department of Vascular Surgery, Zhongshan Hospital, Fudan University, Shanghai 200032, China
胸主动脉夹层是一种高死亡率、多并发症的心血管疾病,在临床上的主要手术治疗方式为胸腔内修复术(thoracic endovascular aortic repair, TEVAR)[1]。然而,对于累及主动脉弓及其弓上分支血管的复杂病例,常规的TEVAR手术由于受锚定区域的限制无法达到良好疗效。
2004年,McWilliams等[2]首次将结合开窗技术的TEVAR术(in situ fenestration-TEAVR, ISF-TEVAR)应用于临床,成功重建左锁骨下动脉(left subclavian artery, LSA)。临床上对于夹层近端破口靠近LSA根部的复杂性病例,为保证主体覆膜支架在主动脉内的锚定,降低术后夹层逆向撕裂等并发症的风险,患者的LSA入口通常会被覆膜支架封堵;通过在主体支架封堵LSA的部位进行开窗,植入开窗支架重建LSA,从而保证术后左侧上肢正常供血[3]。开窗技术的应用,有效拓展了TEVAR手术的适用范围。
近年来随着医学成像和体内测量技术的发展,个性化血液流动数值模拟已成为研究主动脉夹层发病机理和评价术后疗效的有效方法。Kandail等[4]对比分析分支支架和开窗支架对腹主动脉血流的影响。然而,关于胸主动脉ISF-TEVAR术后的血液动力学参数变化,仍鲜有报道。
本文首先对一例主动脉夹层患者建立ISF-TEVAR术后主动脉模型,基于双流体模型开展血液两相(血浆、红细胞)数值模拟,获取血流动力学参数,量化评估ISF-TEVAR手术疗效;另外通过调整开窗支架在主动脉弓部的伸出长度,虚拟构建两例“半伸出”和“无伸出”的术后模型,探究支架伸出长度对血液流动的影响,为改进手术方案提供理论依据。
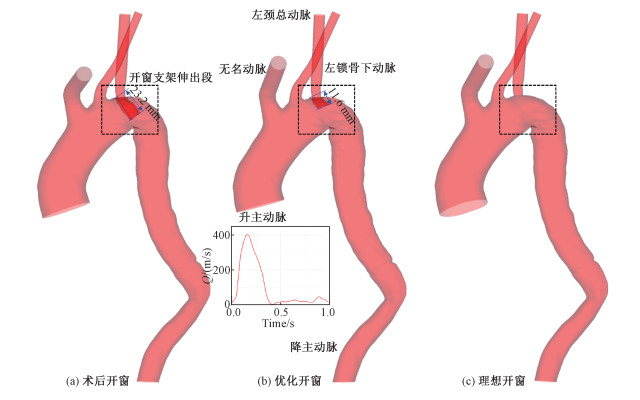
1 几何模型与数值模型 1.1 几何模型本文选取由复旦大学中山医院提供的一例Stanford B型夹层,破口位置距离LSA不足15 mm,为保证锚定充足,支架完全覆盖左锁骨下动脉入口,同时为保证左侧上肢供血,另行原位开窗,在LSA内植入开窗支架。通过CTA扫描获取术后影像资料,三维重建的主动脉几何模型如图 1(a)所示,术后LSA血流通畅,近端夹层假腔消失,重塑良好。
|
Download:
|
| 图 1 重建的ISF-TEVAR术后主动脉模型 Fig. 1 Reconstructed aortic geometries after ISF-TEVAR | |
同时为探究开窗支架伸出长度对血液流动的影响,本文通过虚拟手术构建两例术后模型。首先将开窗支架在主动脉弓内的伸出长度缩短为原长的50%(11.6 mm),构建“半伸出”的优化开窗模型,然后完全消除开窗支架的伸出段,构建“无伸出”的理想开窗模型。通过对比分析血液动力学参数,定量考察支架伸出长度的影响,为改进手术方案提供理论支撑。
1.2 数值模型本文将血液假定为红细胞悬浮于血浆的两相系统[5],其中将红细胞设为球形刚性固体颗粒,假定血浆为不可压缩的非牛顿流体,即将血液简化为包含血浆和红细胞的两相非牛顿流体,忽略血小板、白细胞等体积分数低于1%的组分。非牛顿黏性模型可以捕获血液的剪切稀化现象,本文利用修正的Carreau-Yasuda模型描述血液的非牛顿特性,该模型考虑了剪切率和红细胞体积分数对血液黏性的影响[5]。Schiller-Naumann模型被广泛应用于多相流动中相间动量交换系数的确定[6],本文采用该模型计算血浆与红细胞的相间作用力。假定血管壁为刚性无滑移,忽略血管壁与血液的相互作用。详细的模型介绍已经发表在之前的研究中[7]。
2 边界条件与求解过程由于无法获取升主动脉入口流速测量数据,因此选取文献中的脉动速度函数作为进口边界条件[8]。进出口处红细胞体积分数恒定为45%[9],出口(包括降主动脉、无名动脉、左颈总动脉、左锁骨下动脉)均采用弹性腔模型,根据前人的方法[10]确定模型参数。流场方面,连续相(血浆)采用剪切应力输运模型,离散相(红细胞)设置为零方程模型[11]。
本文通过ICEM绘制3个算例的计算网格,网格数均大于3百万,近壁面区域设置5层边界层。利用收缩期峰值时刻的壁面剪切力变化验证网格无关性,结果表明选定网格与细网格模拟结果之间的差异均小于3%,因此认为本文网格数量选择合理。
控制方程采用有限体积法进行空间离散,迭代计算采用经典的Phase Coupled SIMPLE算法,计算基于ANSYS Workbench平台,两相非牛顿流体模型和弹性腔模型通过CEL语言添加到CFX中,时间步长取0.001 s,连续计算3个周期,取第3个周期的计算结果进行分析。
3 模拟结果分析 3.1 血液流场血液供应与人体组织的生理功能关系密切。图 2展示收缩期峰值时刻的血液流线以及速度云图。术后进入无名动脉和左颈总动脉的血液出现加速现象,值得注意的左锁骨下动脉内流线较少,每搏动血液流量为2.50 mL/s,仅占升主动脉总流量的2.36%,可能导致相关血管灌注不良;开窗支架伸出段底部的血液出现加速,同时在支架伸出段后方形成低速区,尾部流线较为混乱。优化开窗后(图 2(b)),左锁骨下动脉内的流线明显增多,每搏动流量升至4.25 mL/s,主动脉弓部流速分布趋于均匀,而LSA入口附近的高速区贴近壁面;左颈总动脉内的流线略微减少,血液速度也有所降低。理想开窗(图 2(c))中,流经左锁骨下动脉的血液进一步增加,达到6.51 mL/s,LSA入口速度分布更加均匀且流线趋于稳定,表明左锁骨下动脉的血液供应得到进一步改善。因此,ISF-TEVAR术可保留左锁骨下动脉,但其血液供应不足,随着支架伸出长度的缩短,左锁骨下动脉供血得到明显改善。

|
Download:
|
| 图 2 收缩期峰值时刻血液速度流线及云图对比 Fig. 2 Comparison of streamlines and contours at peak systole | |
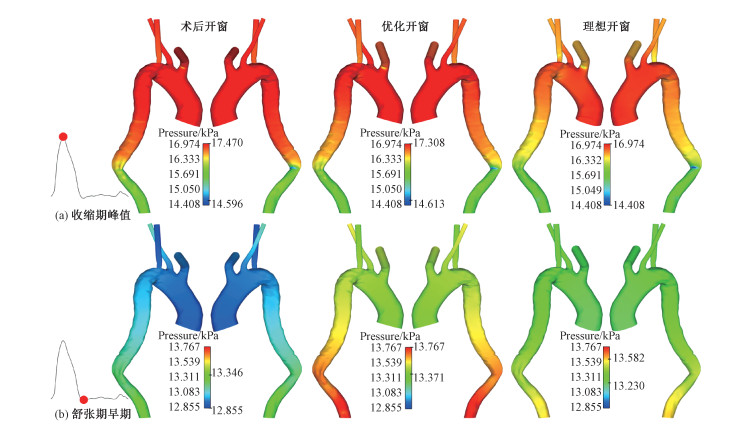
图 3显示流速峰值时刻和舒张期早期的壁面压强分布对比。收缩期峰值,术后开窗模型的压力沿主动脉轴向方向降低,升主动脉、主动脉弓以及降主动脉近端受到的血流冲击作用最强,壁面压强高,值得注意的是相对于其他弓上分支,左锁骨下动脉的壁面压力较低;随着支架伸出长度的缩短,高压区域逐渐收缩,压力峰值也依次降低,在理想开窗模型中,高压区仅包含升主动脉和部分主动脉弓。舒张期早期,主动脉处于低压状态,术后开窗模型壁面压力分布均匀,沿主动脉轴向方向逐渐升高;优化开窗后,主动脉区域压力幅值整体升高;理想开窗中,压力范围进一步收缩,分布更加均匀。
|
Download:
|
| 图 3 壁面压强分布对比 Fig. 3 Comparison of wall pressure distribution | |
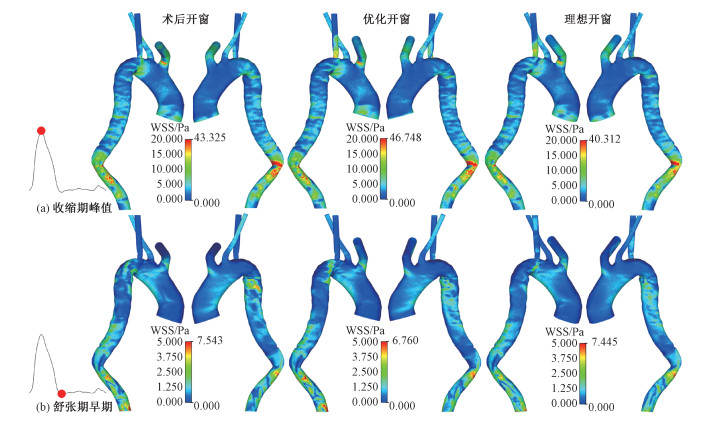
壁面剪切力体现血液对血管壁的冲刷强度。图 4对比不同时刻的壁面剪切力分布。收缩期峰值时刻,在术后开窗的降主动脉远端狭窄区域观察到高剪切力,而左锁骨下动脉壁面剪切力处于较低水平;随着支架伸出长度的缩短,剪切力分布趋势基本一致,值得注意的是剪切力峰值先升后降,同时由于流经左锁骨下动脉的流量增强,其壁面剪切力升高。进入舒张期后,壁面剪切力分布相对均匀,降主动脉近端和远端剪切力较高;优化开窗后,剪切力峰值降低,壁面分布更加均匀;在理想开窗中,剪切力峰值出现回升。
|
Download:
|
| 图 4 壁面剪切力分布对比 Fig. 4 Comparison of wall shear stress distribution | |
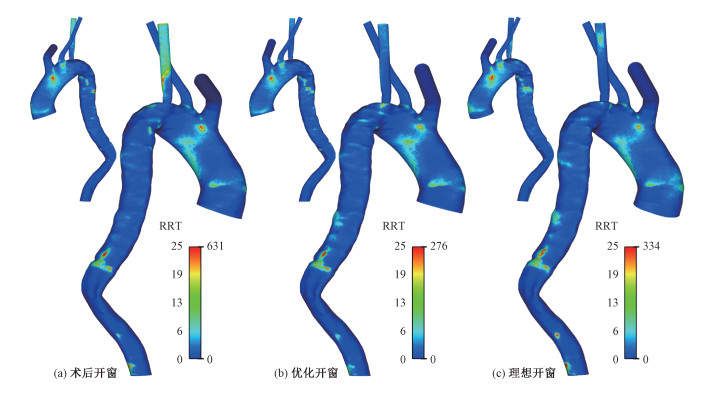
相对停滞时间(relative residence time, RRT)与血栓形成位置的关系密切[12],RRT值越高表示血液在该区域的停留时间越长。图 5展示血液RRT的壁面分布。在术后的主动脉弓、重建的左锁骨下动脉以及降主动脉远端狭窄区域可以观察到高RRT,表明上述区域形成血栓的风险较高,且血液在左锁骨下动脉内的停滞时间较长;优化开窗后,RRT的整体分布趋势大体相似,值得注意的是由于支架伸出长度的缩短,RRT峰值出现下降,同时血液在左锁骨下动脉的停滞时间明显降低;在理想开窗中,RRT峰值略微上升,左锁骨下动脉远端的RRT局部升高。
|
Download:
|
| 图 5 血液停滞时间分布对比 Fig. 5 Comparison of relative residence time distribution | |
目前在ISF-TEVAR手术中,关于LSA开窗支架的伸出长度没有明确的标准,主要依据医生的临床手术经验。本文模拟结果表明缩短支架伸出长度有利于保障LSA的血液供应,降低对主动脉弓部流场的干扰。在临床上,适当缩短LSA开窗支架伸出长度是可行的,复旦大学附属中山医院血管外科已将开窗支架伸出长度控制在1 cm左右,同时为保证开窗结构的安全稳定,应当在开窗支架内部额外放置一个球囊可扩张支架。
文献表明,相对于单相血液模型,本文采用的两相模型可以更加准确地模拟血液流动[13]。然而仍存在以下不足:首先没有考虑血液与血管壁之间的耦合作用;其次模拟的边界条件不是病人的个性化测量数据;最后本文仅研究了一例具有代表性的患者,未来需要更大的样本验证本文的结论。
4 结论本文从血流动力学角度初步探讨ISF-TEVAR手术效果,该手术基本实现了重建左锁骨下动脉的目标,但数值模拟结果表明术后左锁骨下动脉的血液供应较低,且支架伸出段尾部的血液流动出现紊乱;同时通过虚拟手术构建两例“优化”和“理想”的术后模型,对比流速、壁面压力、剪切力以及相对停滞时间可以发现,主动脉弓内开窗支架伸出段的存在对血液流动存在明显干扰,缩短支架伸出长度有助于血液的正常供应和稳定流动。
| [1] |
Nienaber C A, Divchev D, Palisch H, et al. Early and late management of type B aortic dissection[J]. Heart, 2014, 100(19): 1491-1497. Doi:10.1136/heartjnl-2013-305133 |
| [2] |
Mcwilliams R G, Murphy M, Hartley D, et al. In situ stent-graft fenestration to preserve the left subclavian artery[J]. J Endovasc Ther, 2004, 11(2): 170-174. Doi:10.1583/03-1180.1 |
| [3] |
Glorion M, Coscas R, Mcwilliams R G, et al. A comprehensive review of in situ fenestration of aortic endografts[J]. Eur J Vasc Endovasc Surg, 2016, 52(6): 787-800. Doi:10.1016/j.ejvs.2016.10.001 |
| [4] |
Kandail H, Hamady M, Xu X Y. Comparison of blood flow in branched and fenestrated stent-grafts for endovascular repair of abdominal aortic aneurysms[J]. J Endovasc Ther, 2015, 22(4): 578-590. Doi:10.1177/1526602815587261 |
| [5] |
Jung J, Hassanein A, Lyczkowski R W. Hemodynamic computation using multiphase flow dynamics in a right coronary artery[J]. Ann Biomed Eng, 2006, 34(3): 393. Doi:10.1007/s10439-005-9017-0 |
| [6] |
Schiller L. A drag coefficient correlation[J]. Zeit Ver Deutsch Ing, 1933, 77: 318-320. |
| [7] |
曾宇杰, 罗坤, 樊建人, 等. 主动脉夹层血液两相流动数值模拟分析[J]. 工程热物理学报, 2016, 37(4): 780-784. |
| [8] |
Gallo D, Lefieux A, Morganti S, et al. A patient-specific follow up study of the impact of thoracic endovascular repair (TEVAR) on aortic anatomy and on post-operative hemodynamics[J]. Computers & Fluids, 2016, 141: 54-61. |
| [9] |
Dill D B, Costill D L. Calculation of percentage changes in volumes of blood, plasma, and red cells in dehydration[J]. J Appl Physiol, 1974, 37(2): 247-248. Doi:10.1152/jappl.1974.37.2.247 |
| [10] |
Pirola S, Cheng Z, Jarral O A, et al. On the choice of outlet boundary conditions for patient-specific analysis of aortic flow using computational fluid dynamics[J]. J Biomech, 2017, 60: 15-21. Doi:10.1016/j.jbiomech.2017.06.005 |
| [11] |
Ansys C. Solver theory guide[J]. Ansys CFX Release, 2006, 11: 1996-2006. |
| [12] |
Cheng Z, Riga C, Chan J, et al. Initial findings and potential applicability of computational simulation of the aorta in acute type B dissection[J]. J Vasc Surg, 2013, 57(2): 35S-43S. Doi:10.1016/j.jvs.2012.07.061 |
| [13] |
Xie H, Zhang Y. The effect of red blood cells on blood heat transfer[J]. International Journal of Heat and Mass Transfer, 2017, 113: 840-849. Doi:10.1016/j.ijheatmasstransfer.2017.05.112 |
 2020, Vol. 37
2020, Vol. 37 


