球床模块式高温气冷堆(high temperature gas-cooled reactor-pebble bed modules,HTR-PM)因其突出的安全特性和出口温度高的优势,既可用于安全高效发电,又可提供高温工艺热,为核能在更广阔的范围内替代化石燃料、促进温室气体减排开辟了新的技术空间,在未来能源系统中具有广阔的应用和发展前景,已得到国际核能界的广泛重视[1]。
准确可靠的反应堆热工水力分析在球床模块式高温气冷堆的设计上占有十分重要的地位,传统上球床模块式高温气冷堆的热工水力分析所用的程序主要是德国于利希研究中心(Jülich)为高温气冷堆研发的Thermix系统分析软件[2]。Thermix[2]采用二维轴对称局域非热平衡多孔介质模型,各程序模块有明确的分析目标及边界,固相球床和冷却剂的温度场单独求解后模块之间耦合计算,但Thermix模型目前不能考虑各个方位角的温度分布[3]。随着计算机性能的提高,计算流体动力学(CFD, computational fluid dynamics)方法在反应堆研究中得到广泛的应用[4-8],许多学者[9-13]采用CFD软件研究分析先进反应堆堆芯的相关热工水力过程,得到比较好的二维计算结果,但三维整体模拟分析还较少。
二维模型一般是针对球床堆芯的流动换热,较少考虑反应堆侧壁控制棒等于堆芯之间的耦合换热影响,为了精准模拟堆芯流动换热过程,本文对高温气冷堆堆芯进行三维建模,建立氦气上升通道、顶部混合区、控制棒通道、堆芯、压力容器侧壁的几何模型,其中堆芯采用多孔介质模型简化。三维模型将每个计算域进行耦合后再计算求解,充分考虑各个模块(氦气通道,堆芯、侧壁、控制棒通道等)之间的相互耦合影响。基于建立的耦合三维模型,本文在额定工况下对堆芯一回路进行稳态三维数值模拟计算,得到堆芯冷却剂的温度场分布,通过对比分析三维模型的计算结果和堆芯冷却剂的温度场分布,并将计算结果与反应堆设计分析程序Thermix的计算结果对比,验证三维模型的准确性。
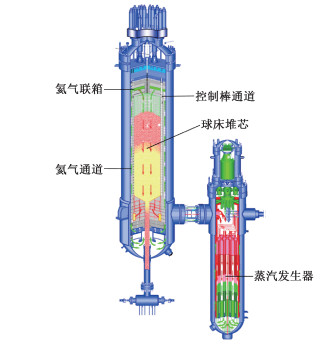
1 球床模块式高温气冷堆简介球床模块式高温气冷堆HTR-PM采用独特的模块式设计,单个模块的堆芯由数万个球形燃料元件组成,四周堆砌石墨块;每个反应堆模块的额定热功率为250 MW,堆芯平均功率密度为3.22 MW/m3。球床堆芯是由约420 000个球形燃料元件堆积组成的近似圆柱形的腔室,堆芯活性区等效高度11 m,外直径约3 m,等效体积约为77.8 m3。在紧靠堆芯的石墨侧反射层中布置了24个控制棒孔道和作为辅助停堆系统的6组吸收球孔道,石墨侧反射层外侧还开有30个冷氦气流通孔道。图 1为HTR-PM的剖面图。
|
Download:
|
| 图 1 高温气冷堆截面图 Fig. 1 Sectional view of the HTR-PM | |
氦气冷却剂在堆芯主要流动换热过程为:氦气冷却剂以96 kg/s的入口流量、7 MPa的入口压力、250 ℃的入口温度进入反应堆压力容器,在反应堆压力容器下部区域混合后大部分气流(>96%)进入30个冷却剂通道,自下而上流入顶反射层内冷氦气联箱;在上部氦气联箱混合后,约3%气体自上而下流入控制棒孔道,作为控制棒的冷却气流;还有约90%氦气自上而下流过球床堆芯和底石墨反射层通道后流入反应堆底部热氦气联箱,在底部热氦气联箱混合后以约750 ℃平均温度流经热气导管进入蒸汽发生器传热管束,约有3%的氦气旁流过燃料卸料管和反射层结构的缝隙。
2 数学物理模型 2.1 模型理论反应堆中存在大量的流动传热过程,计算过程中的数学模型涉及连续性方程、动量方程和能量方程,其中湍流方程选择k-ω SST湍流模型[14],以及多孔介质模型[15]。
各控制方程如下:
1) 连续性方程:
| $ \frac{{\partial \rho {V_x}}}{{\partial x}} + \frac{{\partial \rho {V_y}}}{{\partial y}} + \frac{{\partial \rho {V_z}}}{{\partial z}} = 0, $ | (1) |
2) 动量方程:
| $ \nabla \cdot \left( {\rho {u_x}\mathit{\boldsymbol{u}}} \right) = - \frac{{\partial \rho }}{{\partial x}} + \nabla \cdot \left( {\mu \;\nabla {u_x}} \right) + {S_{{u_x}}}, $ | (2) |
3) 能量方程:
| $ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial x}}\left( {\rho {V_x}{C_P}T} \right) + \frac{\partial }{{\partial y}}\left( {\rho {V_y}{C_P}T} \right) + \frac{\partial }{{\partial z}}\left( {\rho {V_z}{C_P}T} \right)}\\ { = \frac{\partial }{{\partial x}}\left( {K\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {K\frac{{\partial T}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {K\frac{{\partial T}}{{\partial z}}} \right) + {Q_V}, } \end{array} $ | (3) |
4) 湍流模型K方程、ω方程:
| $ \frac{\partial }{{\partial {x_i}}}\left( {\rho k{\mu _i}} \right) = \frac{\partial }{{\partial {x_j}}} \cdot \left( {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right) + {\mathit{\boldsymbol{G}}_k} - {Y_k} + {S_k}, $ | (4a) |
| $ \begin{array}{l} \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {\mu _i}} \right) = \frac{\partial }{{\partial {x_i}}}\left( {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega }. \end{array} $ | (4b) |
式中:σk和σω分别为k和ω的湍流普朗特数;μt为端流黏度;Gk是由平均速度梯度引起的湍动能,由Gk计算得到;Gω由ω引起;Yk和Yω分别是由湍流引起的k和ω的耗散;Dω是交叉扩散系数;Sk和Sω是用户自定义源项。
5) Fluent将多孔介质流动区域的固体结构看作是附加在流体上的分布阻力,通过在标准动量方程中增加一个动量方程源项来模拟,该源项由黏性损失项和惯性损失项组成:
| $ {S_i} = \sum\limits_{j = 1}^3 {{D_{ij}}} \mu {v_j} + \sum\limits_{j = 1}^3 {{C_{ij}}} \frac{1}{2}\rho \left| {{v_i}} \right|{\nu _i}. $ | (5) |
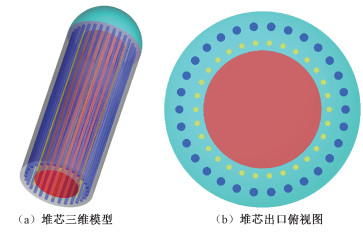
根据已知参数对高温气冷堆堆芯进行三维建模,分别建立氦气上升通道、顶部混合区、控制棒通道、堆芯、压力容器侧壁的几何模型,然后将各个模型进行组合建成整个堆芯三维模型,如图 2所示,其中图 2(b)为堆芯出口俯视图。由于模型的体积大、耦合面多、流动换热过程复杂,为减少网格数量、提高网格质量,总体上三维模型的多处区域采用结构化网格,局部区域采用加密的非结构化网格。
|
Download:
|
| 图 2 高温气冷堆三维模型和俯视图 Fig. 2 Three-dimensional model and vertical view of HTR-PM | |
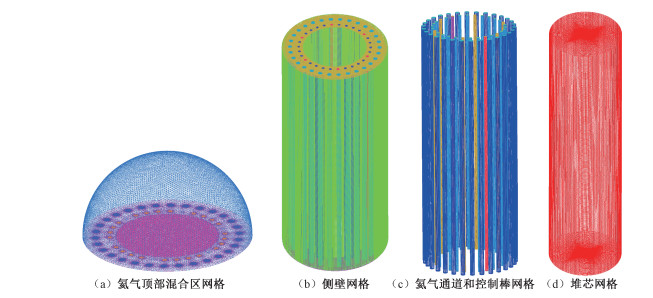
图 3(a)~3(d)分别显示氦气上部混合区网格、堆芯侧壁网格、氦气通道和控制棒网格、堆芯网格。如图 3(a)所示,顶部混合区是半球形的并且结构复杂,因此采用非结构化网格并在交接处对网格进行加密,网格数量为350万,网格质量大于0.75。图 3(b)是堆芯侧壁网格,其通过手动切割块并定义节点数来进行结构化网格划分,网格数量为550万,网格质量大于0.8。氦气通道和控制棒采用O型网格,网格数量为450万,网格质量大于0.85,如图 3(c)所示。球床堆芯是圆柱形,采用O型网格,网格数量为450万,网格质量大于0.9,如图 3(d)所示。将4个部分的网格在ICEM中进行耦合,整合成三维耦合网格模型,然后再在FLUENT中通过interface进行计算域的耦合,最后进行网格无关性验证,验证结果见表 1,最终选择1 800万网格的算例(B)。
|
Download:
|
| 图 3 高温气冷堆三维模型的网格 Fig. 3 The grids of HTR-PM | |
|
|
表 1 网格无关性验证 Table 1 Mesh sensitivity study |
1) 额定工况各参数如表 2所示。
|
|
表 2 HTR-PM热工水力计算主要参数 Table 2 Main calculation parameters of HTR-PM |
2) 孔隙率
由于堆芯内固体空间和流体空间在轴向上的分布是均匀的,因此体空隙率等于面孔隙率。由堆芯的面积及有效流通面积,参考文献[16]可计算得到孔隙率为0.39。
3 热工水力计算结果和分析 3.1 额定功率计算和分析为验证堆芯三维耦合模型的准确性,基于高温气冷堆流动换热过程在额定工况下进行稳态计算,并将计算结果与已发表的THERMIX软件计算结果进行对比。
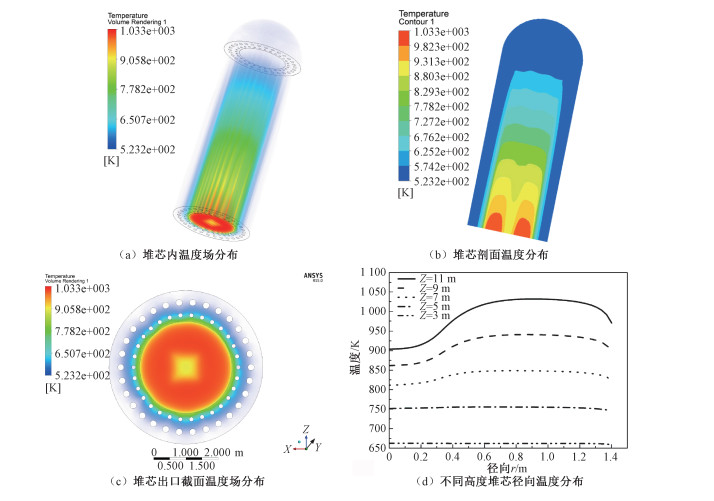
基于建立的堆芯三维耦合模型,利用Fluent等CFD软件,额定功率条件(250 MW,堆芯均匀功率密度分布,S=3.22 MW/m3)下进行堆芯三维热工水力计算。图 4(a)、4(b)给出额定功率条件下堆芯剖面温度分布,4(c)显示氦气冷却剂在堆芯出口处的温度分布云图,4(d)显示堆芯沿轴向不同高度位置时氦气沿径向温度分布。
|
Download:
|
| 图 4 额定功率下堆芯计算结果 Fig. 4 Calculation results of HTR under the full power | |
由图 4(a)~4(c)可以看出,氦气进口温度为250 ℃,随着氦气冷却剂自上而下通过堆芯,不断被加热,氦气冷却剂温度沿堆芯轴向自上而下逐渐升高,在堆芯出口位置达到最高,为759.6 ℃,相比堆芯入口处温度升高约510 ℃。如图 4(d)所示,随着氦气在堆芯内逐渐深入,氦气冷却剂的温度沿堆芯径向分布开始不均匀,距离堆芯中心0.9 m左右温度最高,达到759.6 ℃;堆芯中心处的温度相对较低,约为630.5 ℃。分析认为,堆芯中心处的温度较低的主要原因可能是在高温气冷堆实际结构中,顶部氦气联箱布置了一个主氦风机,推动氦气在顶部联箱中充分混合并均匀进入堆芯。而在三维耦合模型中,顶部氦气联箱被简化为一个半球形结构,氦气冷却剂从冷却剂孔道进入顶部氦气联箱后,在顶部氦气联箱中自然混合,随后向下进入堆芯。因此氦气在半球形顶部联箱中自然混合很可能并不完全均匀,导致进入堆芯中心处氦气流量较多,而靠近壁面处氦气冷却剂流量相对较少,进而造成堆芯中心处温度较低,靠近壁面处温度较高。在进一步的工作中将通过改进顶部氦气联箱的结构和插入UDF程序优化。
表 3进一步对比相同条件下CFD计算结果与Thermix计算结果。可以看出,本研究使用CFD软件针对堆芯三维耦合模型计算获得的氦气出口平均温度与Thermix计算结果符合较好,两个软件计算结果的相对误差为0.21%。对比结果表明,本文构建的堆芯三维耦合模型可以用于球床模块式高温气冷堆的热工水力计算分析。
|
|
表 3 计算结果对比 Table 3 Calculation results using three-dimensional model and Thermix |
额定功率是核电厂正常运行并经常处于的工况,也是反应堆功率调节前的初始状态;而50%额定功率则是核电厂功率调节过程中的重要阶段。50%额定功率的模拟计算,对查看模型在不同功率水平下的计算精度、验证全尺寸堆芯三维耦合模型在不同等工况下的计算能力和稳定性有重要意义。
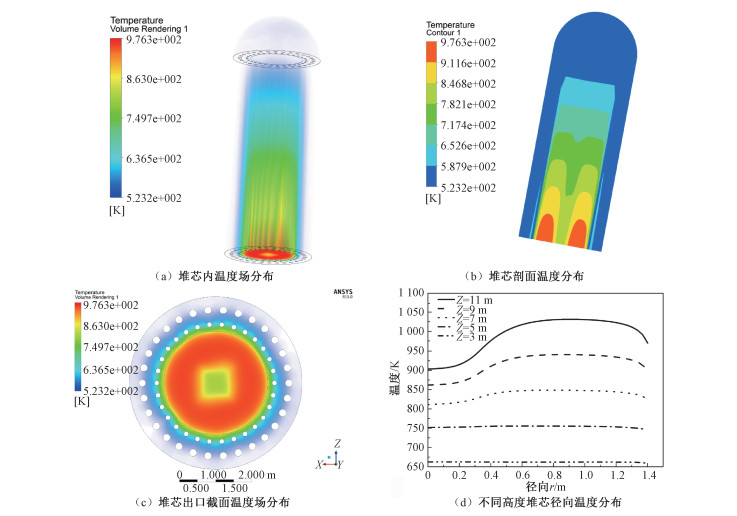
基于全尺寸堆芯三维耦合模型针对50%额定功率进行模拟计算。计算的主要参数:反应堆总功率为125 MW,氦气冷却剂质量流量为48 kg/s。图 5(a)、5(b)和5(c)分别显示50%额定功率下堆芯剖面温度场分布云图和氦气冷却剂在堆芯出口处的温度分布云图,图 5(d)显示50%额定功率下堆芯沿轴向不同高度位置时氦气沿径向温度分布。
|
Download:
|
| 图 5 50%额定功率下堆芯计算结果 Fig. 5 Calculation results of HTR under 50% of the full power | |
由图 5(a)~5(d)可以看出,50%额定功率下,氦气冷却剂在堆芯入口温度为250 ℃,氦气冷却剂温度沿堆芯轴向自上而下逐渐升高,在堆芯出口位置达到最高,为703.3 ℃,相比堆芯入口处温度升高约453.3 ℃。相比满功率工况,堆芯出口截面的平均温度降低56.3 ℃。氦气冷却剂在堆芯出口界面处温度沿径向分布不均匀,距离堆芯中心0.92 m左右温度最高,达到703.3 ℃;堆芯中心处的温度相对较低,约为553.3 ℃。氦气冷却剂通过堆芯带走热量,温度逐渐升高,但在同一平面内中心温度比四周温度低,造成这种结果的主要原因可能是氦气在氦气联箱内混合不充分。总体上看,所得到的温度场能够正确反映高温气冷堆堆芯温度分布,满足模拟仿真的要求。
4 结语本文基于氦气冷却剂在高温气冷堆堆芯流动换热过程,建立高温气冷堆堆芯三维耦合模型。利用CFD通用程序Fluent软件模拟高温气冷堆一回路系统稳态流动换热过程,获得堆芯不同高度位置的径向温度分布。将计算结果与已发表的Thermix软件计算结果进行对比,数值模拟计算结果的相对误差小于1%,表明CFD模型可以精准可靠地计算高温气冷堆堆芯流动换热的热工水力过程。在此基础上,基于构建的三维耦合模型,模拟计算50%额定功率下的高温气冷堆堆芯冷却剂的传热特性,堆芯氦气出口的温度变化符合传热规律。本文研究结果可为高温气冷堆堆芯的热工水力安全分析提供重要的技术支持。
| [1] |
吴宗鑫, 张作义. 世界核电发展趋势与高温气冷堆[J]. 核科学与工程, 2000(3): 211-219. Doi:10.3321/j.issn:0258-0918.2000.03.004 |
| [2] |
Zhou Y, Zhou K, Ma Y, et al. Thermal hydraulic simulation of reactor of HTR-PM based on thermal-fluid network and SIMPLE algorithm[J]. Progress in Nuclear Energy, 2013, 62(8): 83-93. |
| [3] |
Chen F B, Dong Y J, Zhang Z Y. Post-test simulation of the HTR-10 reactivity insertion without scram[J]. Annals of Nuclear Energy, 2016, 92: 36-45. Doi:10.1016/j.anucene.2016.01.023 |
| [4] |
李林森, 王侃, 宋小明. CFD在核能系统分析中应用的最新进展[J]. 核动力工程, 2009, 30(S1): 28-33. |
| [5] |
彭浩然, 孙俊. 高温气冷堆堆芯球床的流动与换热分析[J]. 工程热物理学报, 2016, 37(5): 1076-1083. |
| [6] |
Anderson N, Hassan Y, Schultz R. Analysis of the hot gas flow in the outlet plenum of the very high temperature reactor using coupled RELAP5-3D system code and a CFD code[J]. Nuclear Engineering and Design, 2008, 238(1): 274-279. Doi:10.1016/j.nucengdes.2007.06.008 |
| [7] |
Ferng Y M, Chi C W. CFD investigating the air ingress accident occurred in a HTGR simulation of thermal-hydraulic characteristics[J]. Nuclear Engineering and Design, 2012, 245: 28-38. Doi:10.1016/j.nucengdes.2012.01.004 |
| [8] |
梁好玉, 武俊梅. 压水堆燃料棒束新型定位格架的数值分析[J]. 中国科学院大学学报, 2018, 35(2): 200-208. |
| [9] |
宋士雄, 魏泉, 蔡翔舟, 等. 基于CFD方法的球床式高温气冷堆稳态热工水力分析[J]. 核技术, 2013, 36(12): 41-47. |
| [10] |
周克峰, 周杨平, 眭喆, 等. 基于流动与传热网络的HTR-PM堆内热工水力模拟[J]. 原子能科学技术, 2012, 46(8): 918-926. |
| [11] |
陈森, 刘余, 田茂林, 等. 基于多孔介质模型的压水堆堆芯温场数值模拟[J]. 核技术, 2015, 38(9): 66-71. |
| [12] |
Oh C, Kim E, Schultz R, et al. Comprehensive thermal hydraulics research of the very high temperature gas cooled reactor[J]. Nuclear Engineering and Design, 2010, 240(10): 3361-3371. Doi:10.1016/j.nucengdes.2010.07.007 |
| [13] |
Wang C, Sun K, Hu L W, et al. Thermal-hydraulic analyses of transportable fluoride salt-cooled high-temperature reactor with CFD modeling[J]. Nuclear Technology, 2016, 196(1): 34-52. |
| [14] |
李洋.高温气冷堆氦气流动及燃料球冷却过程数值模拟[D].北京: 北京化工大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10010-1016323091.htm
|
| [15] |
陈静, 田文喜, 韦宏洋, 等. 基于多孔介质模型的行波堆TP-1堆芯稳态温度场与流场数值模拟[J]. 原子能科学技术, 2013, 47(11): 1966-1970. |
| [16] |
李良星, 李会雄. 多尺寸颗粒堆积多孔介质床有效直径研究[J]. 工程热物理学报, 2014, 35(9): 1785-1788. |
 2020, Vol. 37
2020, Vol. 37 


