2. 中国科学院大学, 北京 100049;
3. 中国地震局地壳应力研究所, 北京 100085;
4. 中国地质科学院, 北京 100037
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Crustal Dynamics, Chinese Earthquake Administration, Beijing 100085, China;
4. Chinese Academy of Geological Sciences, Beijing 100037, China
新冠肺炎COVID-19的爆发并在全国的扩散传播,对中国及国际社会造成了巨大冲击,它比起SARS来势更凶、影响更大,引起了人们的密切关注[1],它在全球的扩散传播更是人们急切关注的问题[2]。Adhikari等[3]从流行病学、起因、临床诊断、预防和控制等方面梳理了截至2020年1月31日的70篇关于新冠肺炎的文献。截至2月28日24时新冠肺炎COVID-19在中国已经累计确诊79251例,韩国、伊朗、意大利、日本等国家疫情也在迅速不断恶化。Heymann和Shindo[4]认为如果疫情发展情况朝着更广泛的社区传播方向变化,世卫组织的遏制消除战略可能需要调整。Danon等[5]认为如果没有控制措施,在英格兰和威尔士这类地方4个月内COVID-19的爆发就可达到高峰。因此,加强对新冠肺炎COVID-19传播动力学的研究,总结经验,预测下一步的发展,是目前全世界共同面对的极其重要的科学课题。
疫情发生后,国内外科研人员对新型冠状病毒的起源和感染性、致病机理、扩散模式等开展了许多工作,对传播动力学模型和预测、防控建议等做了大量研究。这对疫情的判断、决策、治疗起到积极的作用。Li和Feng[6]对中国大陆特别是湖北省的疫情进行数据驱动分析和预测。赵序茅等[7]利用大数据回溯新冠肺炎在全国扩散的趋势和传染系数,从数据上论证中国政府对于疫情扩散强有力的控制能力。许小可等[8]基于地理位置服务所收集到的大规模人口流动数据,对春节前从武汉离开人口的地理分布进行统计分析,为疫情扩散速度、疫情风险评估和预测提供参考。
在传染动力学模拟方面,Chen等[9]从已有数据的可视化展示疫情传播特点,通过建立传染病动力学模型,评估疫情防控措施和预测疫情疾病走势,为疫情防控决策和大众行为提供参考。喻孜等[10]对SIR模型进行修正,研究感染人数的变化趋势和政府行政行为对趋势变化的影响。Boldog等[2]通过模拟计算评估中国境外新冠病毒爆发的风险。Du等[11]利用指数增长模型和随机人员流动模型耦合方法,估计武汉封城前,新冠病毒向中国369个城市流动的风险。Luo等[12]研究绝对湿度在COVID-19传播中的作用,警告单靠季节天气变化不一定会导致COVID-19病例数的下降。
本文将以湖北为例,采用一种离散随机模型对COVID-19传播动力学进行研究。本文离散随机模型研究有两个特点。第一是疫情初期病人人数很少,传播过程中随机起伏影响突出,因此离散随机模型比连续变量确定性常微分方程模型更能反映初期传播特征。第二是本文的方法可以追踪疫情变化,随时间人为努力下传染率参数的变化可以在参数中得到反映,渐进地对疫情发展做出估计预测。
1 方法与一般采用经典的基于连续变量常微分方程的方法[13]不同,我们采用离散变量随机方法[14]。该方法类似于流体力学研究中,虽然用偏微分方程研究连续流体力学运动是经典的方法,但是随着计算技术的发展,也可以用分子动力学追踪单个分子运动,大量分子运动的集合效应与宏观流体运动状态相联系,从另一个角度研究流体的动力学过程和特征。在我们的研究中,每一个病人的潜伏期、感染期、传染人数等都随机产生,其概率遵从一定概率分布。泊松分布被用于传染病研究[15-16]并被Bogaars等[17]应用于SARS二次感染人数研究中,因此本研究也采用泊松分布,各自的期望值要等于该疾病潜伏期、感染期和传染人数实际统计到的平均值。在模拟中,一个病人随机地感染若干病人,被感染的病人在潜伏期后会发病和再传染他人,既有病人在一段时间后会按一定概率痊愈或死亡,新的病人会不断产生而形成传染链。单一的一个模型只是一种可能的情况,未必具有代表意义,因此需要采用蒙特卡洛方法,进行大量(本文中一般1 000次)随机试验,其平均的结果将具有代表意义。
在大量病人条件下,连续变量微分方程描述传染动力学方法已经很成熟并得到有效应用。但是,在新的流行病初起,只有几个、几十个病人的时候,随机事件会对传播动力学产生显著影响。疫情中一个病人平均感染R个人,R是一个重要的参数。由于人为干预和自然因素变化在疫情不同阶段R会变化,没有外力干预条件下每个病人传染多少人被称为基本传染数R0(basic reproduction number)[18]。当R0大于1时,流行病会发展;R0小于1时,流行病将消亡;R0等于1时,流行病将以原来规模持续,不会扩大、但也不会消失。这对于存在大量病人的情况下无疑是正确的。但是,如果只有1个病人,情况会复杂得多。
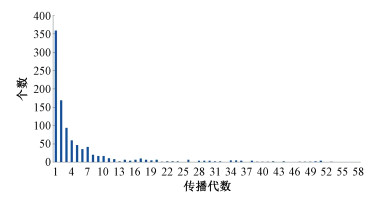
我们进行了简单的离散随机模拟,模型中1个病人会随机感染其他人,感染情况遵从泊松分布[19],虽然平均感染人数即R平均值为1,但也不是确定性的。从第1代1个病人开始,我们随机计算了1 000个可能模型例子。当R0平均值为1时,按泊松分布传染0个人和1个人的概率都是0.367 9、传染2个人的概率是0.183 9、……(表 1)。在实际1 000个试例中,其中有359个模型第1代病人没有能传染任何人,疫情就结束了,170多个模型传到第2代就结束了;共有625个模型在5代以内结束;共有909个模型在第20代以内结束;仅有4个可以传到300代以上(图 1)。这与R0=1可以无限持续下去的期待明显不同。因为如果是一个大的患者群体,例如10 000个病人,那么虽然可能有约3 679个病人0传染,但也有约2 642个病人会传染2个或更多的病人,最后第2代病人总数仍在10 000人左右,可以用连续变量的常微分方程来描述其传染动力学特征。但在只有几个病人的条件下,小概率事件的发生可能造成传染链的大幅度变化。用离散随机模型进行研究,既可以了解总的趋势,又可以对偏差起伏有所了解,在流行病发生的初期应该得到重视和应用。这也揭示出早期追踪传染链得到的表观R0与大规模传播开来时的基本传染数R0未必一致,在早期制定对策时应予注意。
|
|
表 1 基本传染数R0为1时按泊松分布传染不同人数的概率 Table 1 Probability of infected people according to Poisson distribution when the R0 is 1 |
|
Download:
|
| 图 1 基本传染数R0平均值为1的条件下,1 000个随机模型中能传播不同代的模型各有多少 Fig. 1 Maximum infection generations in 1 000 random models with average basic reproduction number R0=1 | |
在知道流行病的平均潜伏期、发病期、死亡率和各个不同时段的每个病人每天有效平均传染率r的条件下,可以进行正演问题的计算,得到每日发病人数的发展变化。在初期自然条件下的每个病人每天传染率r0下,患病人数会急剧增加;当人们采取措施,在不同时段不同程度地减小了有效传染率后,流行病传播速度会降低,每日发病人数会减少乃至疫情消失。然而,在实际问题中更有用的是,在疫情产生后,根据已经获得的一段时间每日发病人数的资料,反演此前一段时间各个时段不同的传染率;然后根据最新的传染率及其可能变化趋势,推测未来疫情的发展变化。在整个疫情期间,不断追踪疫情发展,改进对后续时段传染率的估值,更有效地对后期疫情发展趋势做出不断更新的判断。
下面的研究就包含了这种对前一段的反演和对后一段的预测。目前反演采用的方法是试错法,以后也许可以采用更好的数学方法进行反演。预测中涉及到不同时段r的估值问题,我们在2003年对北京、广州、台湾、新加坡、越南等SARS疫情全过程的反演研究中[14],对于后期传染率r值变化特征获得了一定认识,有助于我们选择适当的r值范围,对疫情可能发展做出预测。
2 资料及预处理我们的资料来源是国家卫生健康委员会(http://www.nhc.gov.cn/xcs/yqfkdt/gzbd_index.s-html)和湖北省卫生健康委员会官方网站(http://wjw.hubei.gov.cn/fbjd/dtyw/)每天公开发布的数据。目前国家和省市卫生健康委员会每天公布的是新增确诊病人的数量,但在传染病传播研究中,更需关注的是每日新发病病人数量。当然,如果能知道每日新增的被感染(但处于潜伏期)的潜在病人数量就更加有利于对疫情的防控。每天发病病人数量并不难获得,确诊时医生了解病人的发病时间、并统计上报即可得到。但是,病人从发病、到就诊、再到确诊有一定的时间滞后(平均约5 d),这样距今大约10 d以内发病的病人还没有全部就诊或确诊,基本完备的数据需要再等10 d才能陆续补充获得。当每天全国确诊人数一度高达数千人时,及时获得每个患者的发病时间和对数据集成统计是十分艰巨的任务[20]。
因此,本文采用排队论方法对每日确诊病人数据进行处理,获得每日新发病和新感染的大致人数。今日确诊的病人,其实从发病到确诊已经等候了多日,每天所占的概率遵从排队论中的Erlang概率分布[21-22]。Erlang分布的概率密度函数为:
| $ {f_{{X_k}}}(x) = \left\{ {\begin{array}{*{20}{c}} {\frac{{{\lambda ^k}{x^{k - 1}}{{\rm{e}}^{ - \lambda x}}}}{{(k - 1)!}}, }&{k = 1, 2, 3, \cdots , x \ge 0;}\\ {0, }&{x < 0.} \end{array}} \right. $ | (1) |
其中有两个参数:k为阶数,影响着函数曲线的形态;λ为速率参数,有时也使用它的倒数均值参数μ。Erlang分布的数学期望为kμ。
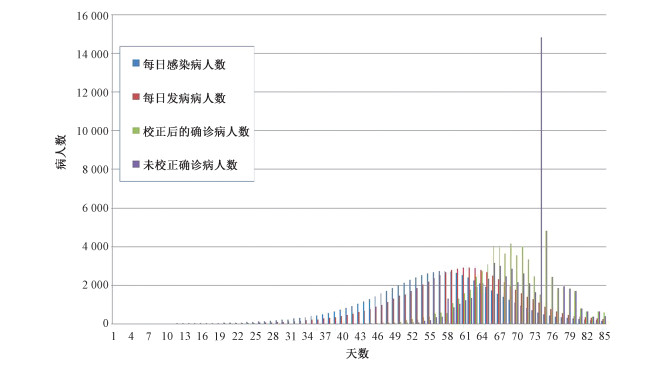
原则上可以将每天确诊病人数按发病到确诊的平均等候时间~5 d遵从Erlang分布,把每日确诊人数数目按概率分配到前面若干天中估计各天发病人数,类似的按潜伏期平均值5.2 d可以进而估算每天感染人数。Mase等[23]在模拟数据延迟系列生成中也采用过Erlang分布。但湖北省数据有两天比较特殊需要单独处理:1) 1月27日确诊病人数目从前一天的371人暴增到1291人,这是武汉医疗条件改善使用核酸检测需要时间缩短的结果;2) 2月12日湖北省确诊病人突然暴增达14 840人,其中仅1 508人是与过去一样基于核酸检测,而13 332人是由把临床诊断确诊病人也纳入确诊统计导致。这两天确诊病人数目激增都是以前多日积累的病人一次性计入导致[24],平均等待时间约为7 d,采用μ值为3.5的二阶Erlang分布分别插值到前几日得到校正的每日确诊人数。基于目前全国患者从发病到确诊的时间间隔平均约为5 d(4.95 d,https://m.chinanews.com/wap/detail/zw/gn/2020/02-17/9095025.shtml),可以采用μ=2.5的二阶Erlang分布处理,得到每日发病人数。潜伏期平均值有不同的估计:包括6.4 d(Backer等[25]对88例统计),5.2 d(Li等[26]对425例统计,Guan等[27]对552例的统计的中位数4 d,按Erlang分布换算)。图 2是从2019年12月1日起[28]到2020年2月23日的原始每日确诊数据、校正后的每天确诊人数、每天发病人数和每天感染人数。
|
Download:
|
| 深紫色为原始资料每日确诊病人数; 绿色为校正后每日确诊人数; 红色为从校正的确诊人数计算的每日发病人数; 蓝色为从每日发病人数计算的每日感染人数。 Dark purple show the number of confirmed patients per day of the original data; green represents the number of confirmed patients per day after corrections; red means the number of patients with newly onset symptom per day calculated from number of confirmed patients, and blue refers to the number of patients newly infected per day based on the number of patients with onset symptom. 图 2 湖北省每日COVID-19确诊人数、发病人数和感染人数 Fig. 2 Daily number of COVID-19 patients confirmed, newly symptom onset and newly infected in Hubei Province | |
在本文的估计中,和实际统计一样,面临一个最近几天发病病人尚未就诊或确诊,因此资料缺失导致发病病人数目会被低估的问题。如果从发病到确诊平均等待时间为5 d且遵从Erlang概率分布,确诊日前8 d以内发病的人数占到85%,10 d以内的达到91%。因此在实际调查中想对近几天每天发病人数得到比较可靠的结果,只有等候大约8~10 d后才能具备较完备的统计资料。但是,如果采用排队论方法估计,我们可以对未来10天确诊人数做不同估计:包括与现今持平、按一定速率比现今减少、或比现今增加,做出不同程度乐观、悲观的多种可能估计,在这些估计的基础上,估算近日每天大约发病人数。
3 结果图 3显示采用我们传染病传播动力学模型得出的1 000个随机模型每天发病人数的平均结果和其对实际数据的拟合,并对今后发展趋势的预测。模型采用试错法反演,得到的传染率r的变化见表 2。模型中的传染率r是每个病人每天平均传染人数,把它在全部有传染能力的日子内加权求和即得到一个病人平均会传染多少个人的传染数R,加权求和是因为在患病后不同时段传染性不同。对COVID-19目前尚没有准确的资料,根据世界卫生组织(WHO)和中国联合调查报告[26],初步得出在这个模型中R≈12.6 r,从传染率r计算出开始阶段的基本传染数R0为6.1~4.0。1月21日开始采取管控措施后最初15天,由于大量的病人超过医疗能力的负担,措施也不是十分到位,有效传染数R仅仅降到0.83,略小于1。由于原来已经存在大量已经感染未发病的患者,因此仍不能抑制发病人数上升的趋势,但是已经从指数上升变为线性上升,初步显示了隔离管控措施的作用。随着措施逐步到位,在全国人民支持下医院收纳能力增强,在随后一周2月8日起R降到0.25,进一步2月14日后又降到0.13。如果保持这样的传染率,预期发病持续(124±7)d,即4月2日前后一周左右结束,如果能进一步把R降低到0.06,有希望在(117±6)d,即3月26日前后一周左右结束。不过从停止发病到门诊和确诊上表现出来可能还要有5 d的滞后。累计发病人数估计为71 000人左右。

|
Download:
|
| 图 3 潜伏期为5.2 d时,采用蒙特卡洛方法和表 1参数的1 000次随机试验的平均结果(红色)与实际每天发病人数(蓝色)的比较,以及在目前有效传染率能继续保持条件下对今后疫情的预测 Fig. 3 Comparison of average result (red) of 1 000 random trials based on Monte Carlo method with the actual number of patients per day (blue). Parameters of model are in Table 1 with incubation period of 5.2 days, and to predict the future epidemic situation under the condition that the current effective R can be maintained | |
|
|
表 2 潜伏期为5.2 d模拟中反演得到的各时间段的传染率r(从2019年12月1日计) Table 2 Values of reproduction rate r in different time periods retrieved fromsimulation when the incubation period is 5.2 d |
我们也进行了参数变化对模型影响的检测。图 4显示改变潜伏期为4.03 d后的拟合结果。模型同样采用试错法反演,得到的传染率r随时间的变化见表 3。潜伏期短的情况下同样的传染率会传播得更快,反过来传染情况已确定的情况下,反演出来的传染率会较低。传染率反演结果给出开始阶段的基本传染数R0为5.0~3.15,低于潜伏期为5.2 d的反演结果约20%。随着隔离管控措施的发挥作用,有效R值也逐渐降低到0.88、038到0.13而使疫情减小。如果保持这样的传染率,预期发病持续(128±14)d。累计发病人数估计为73 000人左右。

|
Download:
|
| 图 4 潜伏期为4.03 d时随机反演平均结果(红色)与实际每天发病人数(蓝色)的比较,以及在目前有效传染率能继续保持条件下对今后疫情的预测 Fig. 4 Comparison of average result (red) of 1 000 random trials with the actual number of patients per day (blue), parameters of the model are shown in Table 3 with incubation period of 4.03 d, and to predict the future epidemic situation under the condition that the current effective R can be maintained | |
|
|
表 3 潜伏期为4.03 d时反演得到的各时间段的传染率r(从2019年12月1日计) Table 3 Values of reproduction rate r in different time periods retrieved fromsimulation when incubation period of 4.03 d |
我们的模型认为2月1日以后有效R值已经小于1。我们不能赞同You等[27]的结果。他们认为2月1日到10日,湖北的有效R值虽然在减小,但只从2.0降到了1.5,他们的结果明显与发病高潮已经在二月初度过的事实相矛盾。
此前,在疫情发展期间,我们运用同样的原则,多次做过这种拟合和预测尝试。图 5是基于截至2月9日的武汉数据做的类似的模拟,可以大体分为模拟段和外推预测段,显示发病高潮已经在二月初度过。当时公布的每日确诊人数还没有包括门诊确诊人数,但是已经连续一周处于每天2 000人以上的高位,发病高峰期还要持续多久是人们普遍关注的问题。而2月12日国家卫健委对统计准则做了新的规定后,将门诊确认的病例纳入确诊人数,因此确切人数日增15 000多人。这虽然影响到每日发病人数和预期感染总人数的估计,但对发病人数峰值已经过去的判断这点仍然符合现在的认识。

|
Download:
|
| 图 5 绿色线条为基于2月9日截止的实际确诊资料计算的每日新增病人人数,红色线条为根据绿色曲线用试错法获得各时段的传播率后的模拟曲线 Fig. 5 The green line shows the daily number of new patients calculated from the number of comfirmed patients up to February 9. The red line is the simulation curve after obtaining the effective r of each period according to the green curve | |
在传染病动力学分析中,使用每日发病人数资料比每日确诊人数更加合理和准确,但从发病到确诊平均有5 d等待时间,人们难以及时获得发病人数信息。本文利用排队论计算每日发病病人数目和每日感染病人数目解决了这一困难。与实际统计资料比较显示了这种方法是可行的。据中国疾病预防控制中心提供的截至2月11日的实际发病统计资料[24],数字表明1月24日进入发病高峰期,2月1日达到发病高峰,日发病人数达3 100余人。本文提出的方法计算结果为1月31日为高峰,峰值约3 000人,与实际统计资料吻合。这种方法不但为传染病动力学模拟提供了基础参数,而且在对潜伏期有所了解的基础上,可以进一步估计每天被感染人数,对疫情发展做出更全面的判断。从图 2可以看出感染高峰、发病高峰和确诊高峰之间存在的滞后关系。
模拟表明,在采取有效的隔离管控措施后,由于已经被感染者陆续发病的滞后效应,有效传染率R不会迅速降低,而且即使R已经降到1以下,发病人数仍会上升。但不再会是指数上升,而转变为线性上升。面对逐日高升或保持在高位的确诊人数,公众会产生焦虑的心态,了解这种特征应该有助于缓解民众的情绪,也为领导做出正确决策判断提供重要参考。
基本传染数R0一直是流行病学研究中十分关注的一个参量,Obadia等[31]基于R语言开发了R0计算软件包,集成了2009年H1N1流感大流行期间最常用的5种疫情传播参数估计方法。本文反演求出的基本传染率R0是一种新的尝试,我们发现R0估计与采用的潜伏期值有关,较长的潜伏期(5.2 d)给出R0为6.1~4.0,采用比它短20%的潜伏期反演的R0也相应低一些,为5.0~3.15。关于R0估计的讨论很多(Ridenhour等[18]),不同的研究者给出的值经常有差别。例如对于COVID-19,Wu等[32]给出R0为2.68,Zhao等[33]给出2.24~3.58。Jung等[34]对6 924个病例的分析给出R0在2.1~3.2。Liu等[35]对COVID-19到1月23日截止的830个病例统计,用指数成长法(EG)和最大似然法(ML)分别求得R0为2.90和2.92,并给出R随时间的变化,从早期的7.93减少到后来的2.60。我们采用的反演方法这种新尝试,总的看来,与其他人的估计还是吻合的,在大规模干预前,也发现R0随时间呈现从大到小的变化,与Liu等[35]的结果类似。但比较起来,我们给出的R值略显偏高。在前面介绍方法时已经谈到,对于大量病人连续变量微分方程分析中R=1时流行病就可以延续的概念,在很少量病人随机模型中并不成立,是否因为这个原因,只有在平均传染率更高时,传染病最初才真有机会得以发展,导致我们求得的R的平均值偏高,或者只是一个偶然个例,其原因尚有待进一步探讨。
我们的研究表明:疫情爆发阶段,由于感染、发病、就诊和确诊存在滞后,已感染人数可以远大于确诊人数。在武汉封城前当日正式报告的确诊患者只有180例,但图 2中显示当日新增被感染人数可能已达2 500人左右,累计被感染人数可能达33 000人,被感染而尚未发病、或病状轻微的患者流向湖北省外各地,成为各地的传染源头,造成全国性的疫情蔓延。据文献统计[35]外地患者中有5 900余人与湖北有直接接触。反之,在目前疫情消退阶段,感染人数和发病人数大大减少,甚至可能低于每日确诊人数。因此不应过分担心春节后回程的农民工和学生诱发大的疫情回弹,只要思想不放松懈怠,分区、分批、错峰安排返程,做好交通工具上的卫生防疫工作,做好接受地的隔离管控安排,不出大纰漏,就可以成功实现复工复课。目前倒是韩国、伊朗、意大利、日本等疫情正在恶化的国家,可能处于类似武汉早期的阶段。因此,我们国家必须对入境人员做好检查和必要的隔离管控。
本研究使用的程序可以在疫情发展不同阶段,跟踪疫情发展,反演传染率的变化,并根据反演的传染率做短期的外推和预测,显示了这个传染病传播动力学模型对复杂疫情发展的适应性,值得进一步发展。但目前本程序还存在一些问题需要改进。最突出的问题是,目前程序正演计算在给定各时间段的传染率r后,从起始到终了的全部可能的概率模型,让它们的平均模型接近实际疫情的数据。然而,在我们追踪计算中,前一段的过程已经结束,那些前一段已经远离平均情况的模型可以被扬弃,只有那些比较接近实际的平均模型的个例们才值得保留,继续运行下去。但是目前程序尚未包含这种功能。这样就出现对疫期内总的感染人数预测时,由于包含那些早就大大偏离实际情况的个例而导致误差偏大。例如图 3的模型预测整个疫期病人总数达71 000±36 000人,其实如果剔除那些前面已经远远偏离实际情况的模型,在仅保留前面时段接近实际情况的那些模型的条件下,误差会小得多。目前的程序也使得平均模型会大幅度不规则地变化,难以建立数学模式进行自动化的反演,停留在试错法反演传染率参数。对程序进一步改进是下一步的一项重要研究内容。
5 结论我们开展了湖北新冠肺炎COVID-19传染动力学研究。研究需要对湖北每日感染人数和每日发病人数了解,然而每日公布的仅仅是确诊数字,原始数据存在较大不确定性。例如,2020年1月27日核酸检验能力的增强,2月12日确诊标准变化、纳入了过去不计入的门诊确诊病例,都造成每日确诊病人数量出现异常高值。我们首先对原始数据进行预处理,然后利用排队论Erlang概率分布,依据医疗界关于从发病到确诊的等待时间为5 d、从感染到发病的潜伏期为5.2 d的认识,从预处理过的确诊数据计算出每日发病人数和每日感染人数。计算的每日发病人数与CDC新近公布的2月12日以前的每日发病人数较好的吻合,说明我们对原始数据的校正和处理方法科学有效。得到的每日发病和感染人数,可以作为传染病动力学模拟的基础数据。
进而开展离散变量随机概率模拟[14],依据每日发病人数,反演疫情发展不同阶段的有效传染率的变化。发现疫情初期基本传染数R0从6.1减少到4.0,每日感染人数急剧指数式增长;在武汉采取封城等有效措施后,有效R值减少到1之下,并随着外部医疗卫生支援的增强、隔离管控措施的逐步落实,R值降低到0.13以下。发病高峰已经在2月初度过,目前虽然不排除疫情会有小的起伏,但只要坚持严格的隔离管控措施,总的趋势就不会变化。预期疫情在3月底前后结束,累计患病人数达到71 000人左右。
研究表明,疫情爆发阶段,发病人数一般大于确诊人数,已感染人数又大于发病人数。那时人口流动的隔离管控措施往往又不到位,容易造成疫情异地传播扩散。春节前武汉五百万人流向湖北省外各地,造成外地患者与湖北有直接接触者达5900余人之众。而在目前消退阶段,未发病的感染人数已经大大减少,因此春节后回程的农民工和学生诱发大的疫情回弹可能性不大。但是韩国、伊朗、意大利、日本等国家正处于疫情可能大规模爆发的阶段,我们国家应该对入境人员做好检查和隔离管控工作。
| [1] |
陈锡康, 杨翠红, 鲍勤, 等. 新冠肺炎疫情对中国经济的影响分析与对策建议[J]. 中国科学院院刊, 2020, 35. Doi:10.16418/j.issn.1000-3045.20200210003 |
| [2] |
Boldog P, Tekeli T, Vizi Z, et al. Risk assessment of novel coronavirus COVID-19 outbreaks outside China[J]. Journal of Clinical Medicine, 2020, 9(2): 571. Doi:10.3390/jcm9020571 |
| [3] |
Adhikari S P, Meng S, Wu Y., et al. A literature review of 2019 novel coronavirus during the early outbreak period: epidemiology, causes, clinical manifestation and diagnosis, prevention and control[J]. Preprints (www.preprints.org). Distributed under a Creative Commons CC BY license, 2020, 20200206: 1-12.
|
| [4] |
Heymann D L, Shindo N. COVID-19:what is next for public health?[J]. The Lancet, 2020, 395(10224): 542-545. Doi:10.1016/S0140-6736(20)30374-3 |
| [5] |
Danon L, Brooks-Pollock E, Bailey M, et al. A spatial model of CoVID-19 transmission in England and Wales: early spread and peak timing[J/OL]. (2020-02-12)[2020-02-25].Available under a CC-BY-NC-ND 4.0 International license. https://doi.org/10.1101/2020.02.12.20022566.
|
| [6] |
Li Q, Feng W. Trend and forecasting of the COVID-19 outbreak in China[J]. arXiv preprint, 2002.05866, 2020.
|
| [7] |
赵序茅, 李欣海, 聂常虹, 等. 基于大数据回溯新冠肺炎的扩散趋势及中国对疫情的控制研究[J]. 中国科学院院刊, 2020, 35. Doi:10.16418/j.issn.1000-3045.20200210002 |
| [8] |
许小可, 文成, 张光耀, 等. 新冠肺炎爆发前期武汉外流人口的地理去向分布及影响[J]. 电子科技大学学报, 2020, 35. Doi:10.12178/1001-0548.2020033 |
| [9] |
Chen B, Shi M, Ni X, et al. Data Visualization Analysis and Simulation Prediction for COVID-19[J]. arXiv preprint: 2002.07096, 2020.
|
| [10] |
喻孜, 张贵清, 刘庆珍, 等. 基于时变参数-SIR模型的2019-nCoV疫情评估和预测[J]. 电子科技大学学报, 2020, 35. Doi:10.12178/1001-0548.2020027 |
| [11] |
Du Z, Wang L, Cauchemez S, et al. Risk for Transportation of 2019 Novel Coronavirus (COVID-19) from Wuhan to Cities in China[J/OL]. (2020-01-28)[2020-02-25]. Available under a CC-BY-NC-ND 4.0 International license. medRxiv, 2020. https://doi.org/10.1101/2020.01.28.20019299.
|
| [12] |
Luo W, Majumder M S, Liu D, et al. The role of absolute humidity on transmission rates of the COVID-19 outbreak[J/OL]. (2020-02-12)[2020-02-25]. Available under a CC-BY-NC-ND 4.0 International license. medRxiv, 2020. https://doi.org/10.1101/2020.02.12.20022467
|
| [13] |
Anderson R M, May R M. Infectious diseases of humans:dynamics and control[M]. Oxford: Oxford Univ. Press, 1991.
|
| [14] |
石耀霖. SARS传播的动力学模型[J].科学通报, 2003, 48(13): 1373-1378. Shi Y L. Stcochastic dynamic model of SARS spreading[J]. Chinese Science Bulletin. 2003, 48(13): 1287-1292. |
| [15] |
Ball F G, Barbour A D. Poisson approximation for some epidemic models[J]. Journal of Applied Probability, 1990, 27: 479-490. Doi:10.2307/3214534 |
| [16] |
Lefkvre C, Utev S. Mixed Poisson approximation in the collective epidemic model[J]. Stochastic Processes and their Applications, 1997, 69: 217246. |
| [17] |
Bogaards J A, Putter H, Weverling G J, et al. The potential of targeted antibody prophylaxis in SARS outbreak control:a mathematic analysis[J]. Travel Medicine and Infectious Disease, 2007, 5: 70-78. Doi:10.1016/j.tmaid.2006.01.007 |
| [18] |
Ridenhour B, Jessica M K, Shay D K. Unraveling R0:considerations for public health applications[J]. American Journal of Public Health, 2014, 104(2): 32-41. |
| [19] |
Frank B, Barbour A D. Poisson approximation for some epidemic models[J]. Journal of Applied Probability, 1990, 27(3): 479-490. Doi:10.2307/3214534 |
| [20] |
Lipsitch M, Riley S, Cauchemez S, et al. Ferguson, managing and reducing uncertainty in an emerging influenza pandemic[J]. The New England Journal of Medicine, 2009, 361: 112-115. Doi:10.1056/NEJMp0904380 |
| [21] |
Champredon D, Dushoff J, Earn D. Equivalence of the Erlang-distributed SEIR epidemic model and the renewal equation[J]. SIAM Journal on Applied Mathematics, 2018, 78(6): 3258-3278. Doi:10.1137/18M1186411 |
| [22] |
Krylova O, Earn D J D. Effects of the infectious period distribution on predicted transitions in childhood disease dynamics[J]. Jouranal of the Royal Socity Interface, 2013, 10(84): 20130098. Doi:10.1098/rsif.2013.0098 |
| [23] |
Masè M, Faes L, Nollo G, et al. Determination of synchronization of electrical activity in the heart by Shannon entropy measure[C]//Proceedings of the First International Meeting on Applied Physics (APHYS-2003). October 13-18.2003. Badajoz, Spain. Recent Advances in Multidisciplinary Applied Physics, Elsevier. Mendezvilas Amsterdam, 2005.235-239. https://doi.org/10.1016/B978-008044648-6.50038-0.
|
| [24] |
中国疾病预防控制中心新型冠状病毒肺炎应急响应机制流行病学组. 新型冠状病毒肺炎流行病学特征分析[J]. 中华流行病学杂志, 2020, 41(2): 145-151. Doi:10.3760/cma.j.issn.0254-6450.2020.02.003 |
| [25] |
Backer J A, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20-28 January 2020[J]. Euro Surveillance, [2020-02-25]. https://doi.org/10.2807/1560-7917.ES.2020.25.5.2000062.
|
| [26] |
Li Q, Guan X, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia[J]. The New England Journal of Medicine, January 29, 2020, doi: 10.1056/NEJMoa2001316.
|
| [27] |
Guan W, Ni Z, Hu Y, et al. Clinical characteristics of 2019 novel coronavirus infection in China[J]. New England Journal of Medicine, 2020. Doi:10.1056/NEJMoa2002032 |
| [28] |
Huang C, Wang Y, Li X, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China[J/OL]. www.thelancet.com.(2020-01-24)[2020-02-25].https://doi.org/10.1016/S0140-6736(20)30183-5.
|
| [29] |
Report of the WHO-China joint mission on coronavirus disease 2019(COVID-19)[R/OL].(2020-02-28)[2020-03-03]. https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf.
|
| [30] |
You C, Deng Y, Hu W, et al. Estimation of the time-varying reproduction number of COVID-19 outbreak in China[J]. medRxiv, 2020.https://doi.org/10.1101/2020.02.08.20021253.
|
| [31] |
Obadia T, Haneef R, Boëlle P Y. The R0 package:a toolbox to estimate reproduction numbers for epidemic outbreaks[J]. BMC Medical Informatics and Decision Making, 2012, 12(1): 147. Doi:10.1186/1472-6947-12-147 |
| [32] |
Wu J, Leung K, Leung G M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study[J/OL]. Lancet.[2020-03-03]. https://doi.org/10.1016/S0140-6736(20)30260-9.
|
| [33] |
Zhao S, Lin Q, Ran J, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020:a data-driven analysis in the early phase of the outbreak[J]. International Journal of Infectious Diseases, 2020, 92: 214-217. Doi:10.1016/j.ijid.2020.01.050 |
| [34] |
Jung S-M, Akhmetzhanov A R, Hayashi K, et al. Real-time estimation of the risk of death from novel coronavirus (COVID-19) infection: inference using exported cases[J/OL]. Clinical Medicine. 2020, 9, 523[2020-02-24].https://doi.org/10.3390/jcm9020523.
|
| [35] |
Liu T, Hu J, Kang M, et al. Transmission dynamics of 2019 novel coronavirus (2019-nCoV)[J/OL]. bioRxiv 2020.(2020-01-25)[2020-02-24]. https://doi.org/10.1101/2020.01.25.919787.
|
 2020, Vol. 37
2020, Vol. 37 


