2. 中国科学院软件所, 北京 100080
2. Institute of Software, Chinese Academy of Sciences, Beijing 100080, China
概率图模型,例如贝叶斯网络和马尔科夫网络,已经被广泛应用在人工智能领域[1]。这类图模型用简洁的结构表示复杂的概率分布,在推理和参数学习方面,由于归一化参数的计算量非常大,在最坏情况下为指数级别[2],一般情况下精确计算条件概率的复杂度也为#P完全[3]的。此外,随着变量个数的增加,模型也更加复杂。Poon和Domingos[1]于2011年提出一种新型深度模型结构——和积网络(sum-product network, SPN)来解决上述问题。和积网络(图 1)是有向无环图,它将观测变量作为叶子结点,将“和”与“积”操作作为深度网络的内部结点。和积网络可以在高树宽模型中快速计算精确推理,其推理开销和网络大小成线性关系,具有很强的表达能力和快速推理能力,在计算机视觉[4]、语音识别[5]、自然语言处理[6]等领域均有应用。当前和积网络的研究主要聚焦在结构学习和参数学习等应用方面,而制约其应用发展的理论问题,如SPN有效性、MAP推理复杂性等问题仍未得到根本解决。
|
Download:
|
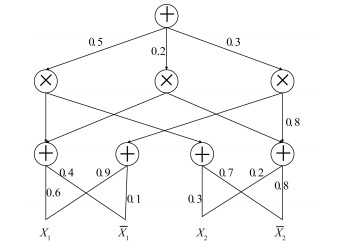
| 图 1 和积网络示例 Fig. 1 An example of sum-product networks | |
和积网络将分布分解为混合(sum)与分解(product)的层次结构,因而可看做基于变量集合的非归一化概率分布。和积网络的有效性(validity)即它可以正确表示概率分布,例如,仅当和积网络有效时,计算联合概率分布px的等式才成立:对
本文的主要工作及其贡献在于:1)探讨和积网络的一些内部结构性质;2)提出验证和积网络的有效性算法及其正确性证明,分析其复杂度和适用场景;3)提出一种新的关于和积网络中生成树个数的计算方式。
1 相关工作和积网络被提出后在基础理论方面、参数学习、结构学习方面以及应用方面都有了相应的研究,从和积网络的基础理论研究方面,Zhao等[10]证明任意和积网络都可以转化为二分贝叶斯网络。Martens和Medabalimi[11]证明网络的表达性随着深度增长而增加。和积网络有效性的定义给出后[1],由于没有相应的验证算法,Peharz[2]弱化有效性的条件要求,证明和积网络的参数可以被转化为局部归一化。一致且完备的和积网络同样保证有效性[12]。Martens和Medabalimi[11]找到有效和积网络的特例,证明Peharz的结论是充分不必要条件,因而强化了有效性的条件,给出强有效性的定义,并证明强有效性与网络输出多重线性多项式的等价关系,而关于和积网络有效性的算法验证的研究仍不充分。本文尝试给出两个验证算法,并比较两个算法的适用场所及复杂度。
从和积网络的权重学习方面,Zhao等[13]提出一种统一的学习和积网络参数的方法。
从和积网络的结构学习方面,Dennis和Ventura[14]提出和积网络的第一个结构学习算法,Adel等[15]提出一种基于SVD分解的算法,通过对样本矩阵进行切割学习和积网络的结构。Rashwan等[16]提出在线贝叶斯矩匹配算法。目前最为常用的算法为LearnSPN[7],虽然提出较早,但由于执行速度快,至今仍被频繁使用,也出现对其改进的算法SPN-BT[8]。目前最好的结构学习算法为ID-SPN[9],通过利用变量之间的间接和直接相互作用、自上而下聚类的方式学习和积网络,该算法将sum结点和product结点作为内部结点,运算电路AC(arithmetic circuits)作为叶结点,从单个AC结构开始,只在直接改善了似然性的情况下将每个AC叶结点拆分为两个新的AC叶结点,最后估计叶结点的分布。由于该算法与AC的基础算法相结合,因而比一般的树形结构如Chow-Liu叶结点更好地逼近复杂的分布。
从应用方面,Cheng等[6]利用和积网络构造语言模型,根据前K个词计算第K+1个词出现的概率,得到比之前语言模型更好的预测准确性。Nath和Domingos[17]引入关系和积网络的概念,并利用关系和积网络构造一个关于缺陷定位问题的易解概率学习模型,可以鉴别重复发生的bug。
和积网络可以进行概率密度估计,因而也被解释为特殊的深度神经网络。同时,它还可以表达一些其他类型的易解概率分布,如稀疏联结树和隐藏树模型。近期,和积网络也被解释为特殊形式的前馈神经网络[4]和概率卷积网络[18]。
和积网络经常被称作一种新型的概率图模型,其性质更像是运算电路。在经典的概率图模型中,叶结点代表随机变量,边代表变量间的依赖关系。然而和积网络的中间结点为运算单元,即“和”与“积”,边决定运算单元的计算顺序,不再关心变量间的关系。
2 和积网络的有效性验证算法和积网络是有向无环图(如图 1),隐藏变量为求和或者求积,并且被交替排列在相邻层次上,sum结点可看作是变量在集合上的混合,product结点可看作是特征的混合,即sum结点提供混合模型,product结点建立特征层次,“有效性”以一种很好的方式约束和积网络,因而网络具有很强的表达能力和推理能力。每一个以和积网络内部结点为根结点的子网络依然为和积网络,和积网络可看作由小的和积网络连接组成,因而在计算上具有潜在的可扩展性,使得学习和推理更加便于处理,在该模型下得到的结果也应用得更加广泛。
现在给出和积网络的形式化定义。
定义1 和积网络[1]:和积网络是一个有根且有权重的有向无环图,内部结点为sum结点与product结点,叶结点为网络输入,输入变量集合为X={X1, …, Xn},X的分布为
令ch(Q)作为结点Q的所有子结点的集合,pa(Q)作为结点Q的所有父结点的集合,desc(Q)为结点Q的所有后代的集合。每条连接sum结点Q与其子结点c∈ch(Q)的边均有非负权重ωQc,令w为和积网络所有权重的集合。SQ是S的子网络,其根结点为Q。网络内所有结点个数设为m。对于X的一个实例x,或者称之为完全示例(complete evidence),用x~X表示。为简化讨论,本文假定随机变量为布尔变量,然而本文结论可被拓展到离散和连续变量。不失一般性,本文假设和积网络有交替的内部结点类型,即sum结点层与product结点层交替出现。
叶结点的范围(scope) [1]是结点对应向量的集合,父结点的范围是所有子结点范围的并集,并把根结点的范围作为和积网络的范围。
和积网络的深度是为sum结点层与product结点层交替出现的和积网络中从根结点到子结点的最长路径长度[1]。
当变量集合X取值为x且和积网络(以下用S表示)有效时,S(x)表示输入为x基于S计算得到的非归一化概率值,即P(X=x)=S(x)/Z,
S(x)在网络中的计算方式为自下而上,x作为叶结点的输入,sum结点的值为子结点值的加权和,product结点的值为子结点值的乘积,最终得到根结点的值作为S(x)的值。如图 1,当X1=1,X2=0,X1=0,
定义2 计算(evaluation)[1]:对于和积网络S,给定变量集合X,X的分布为
| $ {S_Q}(x) = \left\{ {\begin{array}{*{20}{l}} {{\phi _n}\left( {{\mathop{\rm sc}\nolimits} (Q) = {x_{{\rm{|sc}}({\rm{Q}})}}} \right),{\rm{若}}Q为叶结点,}\\ {\sum\nolimits_{c \in {\mathop{\rm ch}\nolimits} (Q)} {} {\omega _{Oc}}{S_c}(x),{\rm{若}}Q为{\rm{sum}}结点,}\\ {\sum\nolimits_{c \in {\mathop{\rm ch}\nolimits} (Q)} {} {S_c}(x),{\rm{若}}Q为{\rm{product}}结点.} \end{array}} \right. $ |
整个网络的值S(x)为根结点的值。
定义3 网络多项式(network polynomial) [13]:令f(·)≥0为基于布尔变量集合X上的概率分布,f(·)的网络多项式是一个关于指示变量的多线性方程
和积网络的有效性即S可以正确表示分布,下面给出有效性的形式化定义。
定义4 有效性[10]:对于和积网络S,给定变量集合X,若对于任意x~X,均有
定义5 完备性,可分解性[1]:和积网络S,令S+为S中所有sum结点的集合,S×为S中所有product结点的集合,则
1) S是完备的当且仅当
2) S是可分解的当且仅当
| $ \operatorname{sc}\left(c_{1}\right) \cap \operatorname{sc}\left(c_{2}\right)=\varnothing。$ |
定义6 拓扑排序(topological sorting) [13]:在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序。
1) 每个顶点出现且只出现1次;
2) 若A在序列中排在B的前面,则在图中不存在从B到A的路径。
2.1 Veri-SPN算法算法1对每个结点都进行验证,计算量较大。首先自下而上标记所有结点的范围,再自上而下,逐层分别检查每个结点的完备性和可分解性,即对于sum结点,检查其子结点的范围是否相同,对于product结点,检查其子结点的范围是否互不相交,通过验证和积网络的完备性和可分解性进而验证有效性,第1个算法为Veri-SPN,具体描述如下。
定理2.1 对结点个数为m,变量个数为n的和积网络S,算法一在Ο(n×m2)内完成验证。
证明 算法1的证明方式为自下而上,设Q1, …, Qm是S所有结点的一个拓扑排序,即k>
当结点Qk为叶结点时,需将该叶结点对应的向量反映在自己的矩阵中,即,若
当结点Qk为product结点时,需要验证Qk的子结点范围互不相同,即
| Algorithm 1 Veri-SPN |
| 1:Find some topological ordering Q1, …, Qm of nodes in SPN 2:For all nodes Qk initialize ak=[ak1, ak2, …, akn]=[0, 0, …, 0], aki∈[0, 1] 3:for k=1:m do 4: b←0 5: if Qk is a leaf node then 6: if 7: aki←1 8: end if 9: end if 10:if Qk is a product node then 11: if Qi∈ch(Qk), i=1:k then 12: if aij=1, j=1:n then 13: if akj=1 then 14: abort 15: else 16: akj←aij 17: end if 18: end if 19: end if 20:end if 21:if Qk is a sum node then 22: if Qi∈ch(Qk), i=1:k then 23: if b=0then 24: akj←aij, j=1:n, b←1 25: else 26: if akj≠aij, j=1:n then 27: abort 28: end if 29: end if 30: end if 31: end if 32:end for |
当结点Qk为sum结点时,需要验证Qk的子结点范围完全相同,即
若和积网络是完备的且是可分解的,则该和积网络是有效的[1],因而算法1可以证明和积网络的有效性。
综上,总的计算成本为Ο(n×m2)。
由于目前没有任何关于m与n关系的探讨,m的取值范围可以是n的多项式范围,也可以是n的指数范围。如果是前者,则算法1在实践中已满足使用需求;相反,如果是后者,在m相当大的情况下,算法1计算量过大。
因而,本文提出第2个验证算法,牺牲一部分准确性,换取相对快速的验证效果,在S的层数低时效果更好。
2.2 Induce-SPN算法有效的和积网络可看做是一些生成树T(induced tree)的叠加,且每个生成树的范围与对应和积网络是相同的,因而对和积网络的有效性验证就可以一定概率转化为对T进行验证,算法2基于上述思想,具体描述如下。
| Algorithm 2 Induce-SPN |
| 1:Let T=(TV, TE) be a subgraph of S 2: 3:while exist node Qk∈TV that 4: if Qk is a sum node then 5: choose exactly one child of Qk in S randomly, put the node in TV, the responding edges in TE 6: end if 7: if Qk is a product node then 8: put all the children of Qk in S in TV in order, the responding edges in TE 9: end if 10: if Qk is a leaf node then 11: skip 12: end if 13: k←k+1 14:end while |
定理2.2 S的范围与T的范围是一样的,并且,T中每个结点的范围与对应的S中结点的范围是一样的。
证明 由于S的根结点Root(S)也是T中的结点,
1) 当S的高度h=2时,若Root(S)是sum结点,则根结点与相邻子结点的范围是一样的,显然,sc(S)=sc(T),若Root(S)是product结点,则Root(S)的所有相邻子结点也在T中,S=T,因而sc(S)=sc(T)。
2) 假设当h=n时,sc(S)=sc(T),那么,当h=n+1时,若Root(S)是sum结点,有k个子结点,则S与每个子网络的根结点的范围一样,同理于T,因而sc(S)=sc(T)。若Root(S)是product结点,则Root(S)与子结点连接的边也在T中,因而sc(S)=sc(T)。
综上,sc(S)=sc(T)。
用同样的方法可以得到,T中每个结点的范围与对应的S中结点的范围是一样的。
定理2.3 若和积网络S是不可分解的,则存在T也是不可分解的。
证明 首先,若S是有效的,则T也是有效的。由于T中所有的sum结点均只有一个子结点,完备性要求sum结点的所有子结点的范围完全相同,因而T天然地满足完备性。T中任意product结点与其子结点均来自于S中的一个product结点及其所有的子结点,由于S是有效的,则所有子结点的范围是互不相交的,由于T的生成过程,T是S的子图,T中每个结点在T中的范围均小于等于在S中的范围,因而,在T中所有子结点的范围依旧是不相交的,满足可分解性要求,所以,T也是有效的。
若S是不可分解的,则存在product结点Qk,其子结点的范围是有交集的,由定理2.2,T中每个结点的范围与对应的S中结点的范围是一样的。因而,若T包含结点Qk,则T包含Qk所有子结点,因而T中Qk的子结点的范围是有交集的,T不可分解。
定理2.4 若S不是完备的,则存在T是不可分解的。
证明 若S不是完备的,则存在结点Qi、Qj有共同的父结点Q,Q为sum结点且sc(Qi)≠sc(Qj)。由于T中每个sum结点只连接一条边,因而Qi、Qj不会出现在同一个T中,则存在Ti、Tj分别包含边(Q,Qj)与边(Q,Qi)。
由于sc(Qi)≠sc(Qj),父结点的范围是子结点范围的并集,因而Q在Ti中与Q在Tj中的范围不一样,然而根据定理2.2,Ti与Tj的范围是一样的(均与S相同),则根据生成树的生成规则,Ti与Tj至少有一个是不可分解的。
定理2.5 若和积网络S不是有效的,则算法2至少以1/fS(1|1)的概率证明S的无效。
证明 尽管存在极端情况,即和积网络S是有效的,但是却不满足完备性或可分解性[11],由于数量极少,故在一般使用中忽略此情况。综上,若S是不可分解的,则存在T是不可分解的,同样,若S是不完备的,也存在T是不可分解的,由于S中所有不同的T的个数为fS(1|1)[13], 根据定理2.2、2.3、2.4,算法2至少以1/fS(1|1)的概率证明S的无效。
算法2的计算复杂度为
下面给出两个算法的具体比较(如表 1所示)。
|
|
表 1 两个算法比较 Table 1 Comparison between the two algorithms |
和积网络中的生成树T为算法2中产生的树:自上而下,首先包含S的根Root(S),若为sum结点则T只包含其中的一个子结点,若为product结点则其所有子结点均在T中,以此类推,直至有一个叶结点包含在T中。Zhao等[13]提到S中T的个数τS仅依赖网络结构,并且远小于2Ο(M),其中M为S中sum结点的个数,并给出τS=Ω(2h),h为S的高度,然而,本文找到的高度为h的最简单结构的和积网络的T个数为22h/2,即:任意高度为h的和积网络,可以得到的个数大于等于22h/2,因而得出更加准确的结论:τS=Ω(22h/2)。
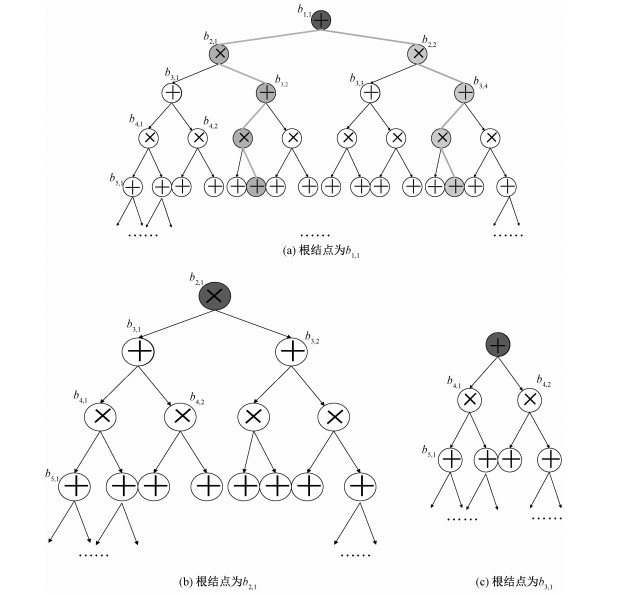
计算过程如下:不失一般性,设Root(S)为sum结点(product结点情况类似,可以类推),设S中sum结点层与product结点层交替出现,并且每个结点的子结点数为2(以此达到最简单的构造S),自上而下对每个结点Nij赋予变量bi, j,i代表层数(i≤h),j代表自左向右的顺序,如图 2(a),bi, j的值代表以结点Nij为根结点的子网络Sij中T的个数。
|
Download:
|
| 图 2 和积网络生成树个数计算步骤 Fig. 2 Calculation steps for the number of generation trees in SPN | |
由于S是对称结构,任意包含边(N11, N21)的T(深灰色)都可以在包含边(N11, N22)的T*(浅灰色)找到一条来对应,且由于T的构造,不存在T同时包含边(N11, N21),(N11, N22)。因而b2, 1=b2, 2,b1, 1=2·b2, 1。如图 2(b), 以N11为根结点的计数问题转化为以N21为根结点的子网络S21中T的计数问题。
由于N21是product结点,因而(N21, N31),(N21, N32)均包含在S21中的任意T中,因而b2, 1=b3, 1·b3, 2,由于S21的对称结构,可得到b3, 1=b3, 2,b2, 1=b3, 12。因而,如图 2(c),以N21为根结点的计数问题转化为以N31为根结点的子网络S31中T的计数问题。
由于N31是sum结点,再次得到b3, 1=2·b4, 1。
综上,得到b2k+1, 1=2·b2k+2, 1,b2k, 1=b2k+1, 12。由于叶结点中T的个数只有一个,因而bh, 1=1。
| $ \begin{aligned} 得到\tau_{S} &=b_{1, 1}=2 \cdot b_{2, 1}=2 \cdot b_{3, 1}^{2} \\ &=2 \cdot\left(2 b_{4, 1}\right)^{2} \\ &=2 \cdot 2^{2} b_{5, 1}^{22} \\ &=2^{2^{0}} \cdot 2^{2^{1}} \cdot 2^{2^{2}} \cdot b^{2 \cdot 2} \\ &=2^{2^{0}} \cdot 2^{2^{1}} \cdot 2^{2^{2}} \cdot b_{7, 1}^{2^{3}} \\ &=\cdots \end{aligned} $ |
若h为奇数,则
| $ \begin{aligned} \tau_{S} &=b_{1, 1} \\ &=2^{2^{0}} \cdot 2^{2^{1}} \cdot 2^{2^{2}} \cdot \cdots 2^{(h-3) / 2} b_{h, 1}^{(h-1) / 2} \\ &=2^{2^{0}+2^{1}+2^{2}+\ldots+2^{(h-3) / 2}}=2^{2^{(h-1) / 2}-1} \end{aligned} $ |
若h为偶数,则
| $ \begin{aligned} \tau_{S} &=b_{1, 1} \\ &=2^{2^{0}} \cdot 2^{2^{1}} \cdot 2^{2^{2}} \cdot \cdots 2^{2^{h / 2}} b_{h, 1}^{L / 2} \\ &=2^{2^{0}+2^{1}+2^{2}+\cdots+2^{h / 2}}=2^{2^{(h+2) / 2}-1} \end{aligned} $ |
综上,
和积网络可以简洁地表示各种边缘分布,其模型的表达能力强,推理速度快,具有广泛应用前景。针对和积网络理论体系中的有效性验证问题,通过分析和积网络的内部结构性质,给出验证和积网络有效性的两个算法及其适用场景,并通过定理证明确保算法的正确性。还提出一种新的和积网络中生成树个数的计算方法。
论文算法1的计算复杂度为Ο(n×m2),与网络结点个数和变量个数相关,利用和积网络能够快速计算边缘分布的特点进行构造。算法2的计算复杂度为Ο(n[h/2]),与网络高度和变量个数相关,首先分析和积网络的内部结构性质,找到网络与生成树之间的关系,根据结构特点进行构造。
现已发现和积网络是特殊形式的前馈神经网络和概率卷积网络。和积网络的应用已经不限制在概率图模型的框架中,将逐渐与深度神经网络一样有广泛的影响。但和积网络的理论体系仍需完善,例如,和积网络中的MAP推理的复杂性,学习和积网络的过程中合适的消耗函数是否存在等问题。
| [1] |
Poon H, Domingos P. Sum-product networks: a new deep architecture[C]//Proceedings of 12th Conf on Uncertainty in Artificial Intelligence, Barcelona, Spain: AUAI, 2011: 2551-2558.
|
| [2] |
Peharz R. Foundations of sum-product networks for probabilistic modeling[D]. Graze: Medical University of Graz, 2015.
|
| [3] |
Roth D. On the hardness of approximate reasoning[J]. Artificial Intelligence, 1996, 82: 273-302. Doi:10.1016/0004-3702(94)00092-1 |
| [4] |
Peharz R, Geiger B, Pernkopf F. Greedy part-wise learning of sum-product networks[C]//Machine Learning and Knowledge Discovery in Databases, Berlin, German: Springer, 2013, 8189: 612-627.
|
| [5] |
Peharz R, Kapeller G, Mowlaee P, et al. Modeling speech with sum-product networks: application to bandwidth extension[C]//International Conference on Acoustics, Speech and Signal Processing, Piscataway, NJ: IEEE, 2014: 3699-3703.
|
| [6] |
Cheng W C, Kok S, Pham H V, et al. Language modeling with sum-product networks[C]//Interspeech, Singapore, 2014: 2098-2102.
|
| [7] |
Gens R, Domingos P. Learning the structure of sum-product networks[C]//Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA: ACM, 2013: 873-880.
|
| [8] |
Vergari A, Mauro N D, Esposito F. Simplifying, regularizing and strengthening sum-product network structure learning[C]//Proceedings of Machine Learning and Knowledge Discovery in Databases, Berlin, German: Springer, 2015: 343-358.
|
| [9] |
Rooshenas A, Lowd D. Learning sum-product networks with direct and indirect variable interactions[C]//International Conference on Machine Learning, Atlanta, GA, USA: ACM, 2014, 32: 710-718.
|
| [10] |
Zhao H, Melibari M, Poupart P. On the Relationship between Sum-Product Networks and Bayesian Networks[C]//Proceedings of International Conference on Machine Learning, Atlanta, GA, USA: ACM, 2015: 116-124.
|
| [11] |
Martens J, Medabalimi V. On the expressive efficiency of sum product networks[J]. Computer Science, 2014, 1: 102-110. |
| [12] |
Peharz R, Tschiatschek S, Pernkopf F, et al. On theoretical properties of sum-product networks[J]. Journal of Machine Learning Research, 2015, 38: 744-752. |
| [13] |
Zhao H, Poupart P, Gordon G. A unified approach for learning the parameters of sum-product networks[C]//Proceedings of the 29th Advances in Neural Information Processing Systems, Barcelona, Spain: MIT Press, 2016, 12: 146-153.
|
| [14] |
Dennis A, Ventura D. Learning the architecture of sum-product networks using clustering on varibles[C]//Advances in Neural Information Processing Systems, Lake Tahoe, Nevada, USA: MIT Press, 2012: 2033-2041.
|
| [15] |
Adel T, Balduzzi D, Ghodsi A. Learning the structure of sum-product networks via an svd-based algorithm[C]//Conference on Uncertainty in Artificial Intelligence, Barcelona, Spain: AUAI, 2015: 32-41.
|
| [16] |
Rashwan A, Zhao H, Poupart P. Online and distributed Bayesian moment matching for parameter learning in sum-product networks[C]//Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, Cadiz, Spain: JMLR, 2016: 1469-1477.
|
| [17] |
Nath A, Domingos P. Learning tractable probabilistic models for fault localization[C]//Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, New Orleans, LA, USA: AAAI, 2016: 1294-1301.
|
| [18] |
Lecun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. Doi:10.1109/5.726791 |
 2020, Vol. 37
2020, Vol. 37 


