2. 中国科学学院大学, 北京 100049;
3. 上海科技大学信息科学与技术学院, 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Information Science & Technology, ShanghaiTech University, Shanghai 201210, China
近年来,随着智能手机和移动设备的大规模普及和随之而来爆炸性增长的富媒体应用,海量的数据产生在通信系统中[1]。根据思科的预测,视频等多媒体数据的通信量将在2021年占据78%的全世界所有移动数据的通信量[2]。此外,移动通信网络通信量随时间高度变化的特性使网络在通信量的高峰期发生严重的系统拥塞,在通信量的低谷期发生极低的系统资源利用率,严重降低通信系统的效率[3]。因此,日益增长的海量数据通信需求给现有的移动蜂窝网络带来极大的压力,例如:回传链路负载不均衡、回传链路信令过载和高网络延迟等问题。
通过把储存资源推送到移动网络边缘,充分利用数据和用户的空间局部特性、用户作息规律的时间局部特性,移动边缘网络缓存被认为是一种极为有效的均衡回传链路负载、降低网络延迟和提高用户体验的技术[4-5]。学术界和工业界在缓存系统算法领域做了大量的研究和探索。网络内容分发提供商通常在缓存内容文件部署阶段使用传统的缓存策略,例如:最久使用策略(least recently used, LRU)[6]、使用频率最少策略(least frequently used, LFU)[7]和这些算法的变体。根据不同时间不同用户可能有不同内容文件喜好的事实,再考虑到移动边缘网络中用户的移动特性,某一特定区域的内容文件流行度常表现出很强的时变特性[8]。因此缓存策略只有能够动态适应内容文件未来流行度分布才能最大限度发挥出移动边缘缓存技术的优势[9]。在缓存内容文件部署阶段对缓存内容文件未来流行度的精确预测是进一步提升移动边缘缓存系统性能的重要突破口[10-11]。
目前,已经有一些文献研究如何预测内容文件的流行度[12-13],但是大多数的研究工作都只局限于内容文件流行度本身。在综合考虑内容文件流行度预测和缓存系统设计的研究中,Bastug等[4]研究如何通过协同滤波的方式预测每个用户对每个内容文件的喜好程度并且把这个反映内容文件流行程度的矩阵应用于蜂窝网络的缓存策略中,但用户的移动特性让这个方法很难在实际系统中实施。此外,Müller等[8]和Li等[9]使用在线学习的方法进行内容文件的主动缓存。但是基于在线算法的缓存系统会因为过于频繁地执行缓存内容文件的部署更新,造成过度的回传链路开销,给系统带来额外的负载压力。另外,由于在线算法收敛速度缓慢,可能无法应对内容文件流行度快速变化的场景。另一方面,基于深度学习的方法给移动边缘网络的性能优化带来了新的思路和更大的性能提升。Wang等[14]将深度强化学习和联合学习的思想用于移动边缘网络中计算、缓存和通信资源的联合优化。Lei等[15]则使用深度神经网络学习缓存内容分发优化算法,使移动边缘网络以最低的能量消耗实现缓存内容分发。
为了应对目前移动边缘网络缓存研究工作存在的不足,并受启发于深度学习带来的数据分析新思路。本文除把储存资源推送到网络边缘,还把计算资源推送到网络边缘,让网络中的每一个接入热点拥有较强的本地数据分析能力,成为智能接入热点,使之可以进行内容文件流行度预测。本文提出一种基于堆叠长短期记忆(LSTM)神经网络精确预测内容文件流行度的方法。预测得到的内容文件流行度信息紧接着被应用于移动边缘网络缓存系统中,提升缓存系统性能,构成完整的深度缓存策略。基于该内容文件流行度预测方法构建的深度缓存策略可以根据不同场景调整缓存系统的缓存内容文件更新频率,灵活高效。基于真实数据集的仿真实验表明,本文提出的内容文件流行度预测方法胜于目前最优的预测方法。依靠深度神经网络精准的内容文件流行度预测信息,移动边缘网络缓存系统的性能得到大幅提升。
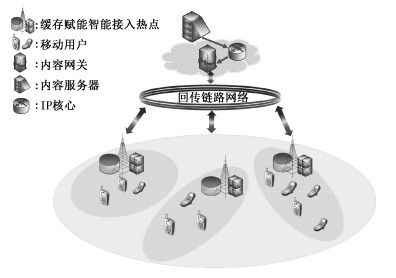
1 系统模型与问题分析 1.1 移动边缘网络缓存框架本文考虑一个由多个缓存赋能智能接入热点组成的移动边缘网络缓存架构。如图 1所示,每一个智能接入热点通过回传链路网络与云数据中心(即内容文件服务器)相连接。本文假设内容文件服务器中有一个有限大的内容文件库F,它的大小为F=|F|。内容文件i∈F的大小为ωi。定义智能接入热点的集合为M={1, 2, …, M}。为了进行高效的缓存内容文件交付,每一个智能接入热点m∈M配备一个大小为Cm的缓存存储器,它可以存储内容文件库中的部分文件
|
Download:
|
| 图 1 移动边缘网络缓存架构 Fig. 1 Mobile edge caching network | |
本文通过把计算资源推送到移动网络边缘的方式使接入热点拥有执行深度学习任务进行本地数据分析的能力(即动态地预测内容文件未来的流行度),使其成为智能接入热点。进而使得网络边缘可以执行深度缓存策略,降低传输时延。
基于深度学习的内容文件流行度预测的主要好处如下:1)由此构建的移动边缘网络缓存系统可以很灵活地控制何时更新缓存、何时预测,有效降低由于频繁执行缓存内容文件部署所造成的回传链路负载;2)深度学习可以提供相对较长一段时间内精确的内容文件流行度预测,进一步提高缓存内容文件交付阶段的缓存命中率,降低传输时延,保证用户体验。这里定义的缓存命中率指的是移动用户的内容文件请求直接被本地智能接入热点服务的次数占所有用户内容文件请求次数的百分比。
1.2 问题分析假设移动边缘缓存网络工作在离散时间tz∈{t1, t2,…,tZ}上。在tz时刻,智能接入热点m根据预测的每一个内容文件在该智能接入热点处的本地流行度和缓存空间Cm更新该智能接入热点的缓存内容。本文定义内容文件i的本地流行度为pi(m, [tz, tz+1)),它表示在未来时间间隔[tz, tz+1)内,内容文件i在智能接入热点m处被请求的次数。K(m, [tz, tz+1))被定义为智能接入热点m处,在时间间隔[tz, tz+1)内总计收到的用户内容文件请求次数,其中第k次被请求的内容文件用i(k)表示,其中1≤k≤K(m, [tz, tz+1))。此外,本文定义智能接入热点m处的缓存状态向量为
| $ \begin{array}{l} \mathit{\boldsymbol{s}}\left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right) = \left[ {{s_1}\left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right), \cdots , {s_F}(m, } \right.\\ {\left. {\left. {\left[ {{t_z}, {t_{z + 1}}} \right)} \right)} \right]^{\rm{T}}}, {\rm{ 其中}}{s_i}\left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right) = \\ \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;内容\;i在{t_2}至{t_{z + 1}}间被缓存\\ 0\;\;\;\;\;\;\;\;\;\;反之 \end{array} \right.. \end{array} $ | (1) |
本文的目标是通过为智能接入热点m找到最优的本地内容文件缓存状态向量s(m, [tz, tz+1))以最大化系统整体的平均缓存命中率。显然,在时间间隔[tz, tz+1)内,智能接入热点m处的平均缓存命中率可以表示为
| $ \begin{array}{*{20}{l}} {{\rm{Hr}}\left( {\mathit{\boldsymbol{s}}\left( {m,\left[ {{t_z},{t_{z + 1}}} \right)} \right)} \right) = }\\ {\frac{{\sum\nolimits_{k = 1}^{K\left( {m,\left[ {{t_z},{t_{z + 1}}} \right)} \right)} {} {I_{s\left( {m,\left[ {{t_z},{t_{z + 1}}} \right)} \right)}}(i(k))}}{{K\left( {m,\left[ {{t_z},{t_{z + 1}}} \right)} \right)}}.} \end{array} $ | (2) |
式中:Is(m, [tz, tz+1))(i(k))为指示函数,若内容文件i(k)在被请求时已被事先缓存至本地智能接入热点m处,函数返回值1,否则为。本文求解的移动边缘网络缓存系统平均缓存命中率最大化问题可以进一步表示为
| $ \begin{array}{l} \max \sum\limits_{z = 1}^Z {\sum\limits_{m = 1}^M \mathit{\boldsymbol{E}} } \left[ {{\mathop{\rm Hr}\nolimits} \left( {{\bf{s}}\left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right)} \right)} \right]\\ {\rm{ s}}{\rm{. t}}{\rm{. }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}} \cdot \mathit{\boldsymbol{s}}\left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right) \le {C_m}, \forall z = 1, \cdots , Z, \\ m \in M, \end{array} $ | (3) |
式中:{s(m, [tz, tz+1))}是优化变量,ω=[ω1, …, ωF]T表示整个内容文件库F中各个内容文件的大小,约束条件用于保证各智能接入热点处缓存不会溢出。
在tz时刻,假设每一个智能接入热点m都可以到未来的tz+1时刻,事先得到其本地每一个内容文件i在未来时间间隔[tz, tz+1)内的流行度信息pi(m, [tz, tz+1)),那么原问题(3)可以等价转换为如下线性规划问题:
| $ \begin{array}{l} \max \sum\limits_{z = 1}^Z {\sum\limits_{m = 1}^M {\sum\limits_{i = 1}^F {{s_i}} } } \left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right) \cdot {p_i}\left( {m, \left[ {{t_z}} \right.} \right., \\ \left. {\left. {{t_{z + 1}}} \right)} \right)\\ {\rm{ s}}{\rm{. t}}{\rm{. }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}} \cdot \mathit{\boldsymbol{s}}\left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right) \le {C_m}, \forall z = 1, \cdots , Z, \\ m \in M, \end{array} $ | (4) |
式中:{s(m, [tz, tz+1))}是优化变量。问题(4)可以针对每一个时间间隔[tz, tz+1)和每一个智能接入热点m更进一步解耦合为Z·M个独立的子问题。每一个子问题都是一个背包容量为Cm、物品数为F的0-1背包问题。一般形式的0-1背包问题是一个典型的NP完全问题,对于一个有n个物品的0-1背包问题,给定解的精确度ε,总可以在时间复杂度Ο(nlog(1/ε)+1/ε4)和空间复杂度Ο(n+1/ε3)解出该问题。此外,一些针对背包问题精巧设计的搜索算法可以找到问题的精确全局最优解[16]。
特别地,若每一个内容文件i都有相同大小(都归一化为单位大小),问题(4)的最优解可以简单地通过时间复杂度Ο(Flog(F))计算得到。也就是根据本地内容文件的流行度pi(m, [tz, tz+1))对内容文件进行排序,选出最受欢迎的Cm个内容文件进行缓存。每个内容文件大小相同的情况在现实系统中常被运用,例如被广泛采用的HTTP(DASH)协议。在这个协议中,每一个内容文件被拆分成相同大小的块,每一块可以认为是一个内容文件。因此,根据本地内容文件的流行度,在缓存内容文件部署阶段可以直接通过对内容文件的流行度排序,选择最受欢迎的Cm个内容文件缓存。在缓存内容文件交付阶段,对于与智能接入热点m相连接的移动用户u的内容文件请求,智能接入热点m先确认用户请求的内容文件是否已经事先被缓存。如果该文件已经被提前缓存,那么该用户的请求会被智能接入热点从本地缓存存储器直接快速响应。反之,用户请求的内容文件会从远程的内容服务器经过回传链路网络回传至本地,然后服务该用户请求。这种情况在通信量高峰时期会造成很高的网络时延,给系统带来很大的回传链路负载。因此,根据内容文件未来的流行度信息,在有限的缓存空间中缓存最受欢迎的内容文件是提升系统性能的关键。不幸的是内容文件未来的流行度信息无法在现有移动边缘网络中提前获得,需要移动边缘网络根据观测到的信息来预测。本文受到深度学习在数据分析上优良表现的启发[17],提出一种使用深度神经网络精确预测内容文件流行度的方法。
2 基于深度学习的内容文件流行度预测根据深度学习的框架预测内容文件的流行度包括模型训练和预测两个阶段。在本文所提的深度缓存策略中,内容文件流行度预测模型的训练采用离线训练的方式进行。训练完成后的模型参数被存储在各个智能接入热点中,用于本地内容文件流行度预测。在模型预测阶段,智能接入热点根据收集的本地内容文件历史信息周期性地预测内容文件未来流行度,用于深度缓存策略决策。下面将详细介绍本文提出的堆叠长短期记忆神经网络内容文件流行度预测模型。
2.1 长短期记忆神经网络与标准形式的循环神经网络相比,长短期记忆神经网络在结构上多了一系列门单元。具体来说,每一个长短期记忆神经网络单元在t时刻由一系列门单元组成,包含:输入门et,输出门ot和遗忘门at。每一个长短期记忆神经网络单元可以如下表示:
| $ \begin{array}{l} {\mathit{\boldsymbol{a}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_a} \cdot {{\left[ {\mathit{\boldsymbol{h}}_{t - 1}^{\rm{T}}, \mathit{\boldsymbol{x}}_t^{\rm{T}}} \right]}^{\rm{T}}} + {\mathit{\boldsymbol{b}}_a}} \right), \\ {\mathit{\boldsymbol{e}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_e} \cdot {{\left[ {\mathit{\boldsymbol{h}}_{t - 1}^{\rm{T}}, \mathit{\boldsymbol{x}}_t^{\rm{T}}} \right]}^{\rm{T}}} + {\mathit{\boldsymbol{b}}_e}} \right), \\ {\mathit{\boldsymbol{o}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_o} \cdot {{\left[ {\mathit{\boldsymbol{h}}_{t - 1}^{\rm{T}}, \mathit{\boldsymbol{x}}_t^{\rm{T}}} \right]}^{\rm{T}}} + {\mathit{\boldsymbol{b}}_o}} \right), \\ {{\mathit{\boldsymbol{\hat c}}}_t} = \tanh \left( {{\mathit{\boldsymbol{W}}_c} \cdot {{\left[ {\mathit{\boldsymbol{h}}_{t - 1}^{\rm{T}}, \mathit{\boldsymbol{x}}_t^{\rm{T}}} \right]}^{\rm{T}}} + {\mathit{\boldsymbol{b}}_c}} \right), \\ {\mathit{\boldsymbol{c}}_t} = {\mathit{\boldsymbol{a}}_t}*{\mathit{\boldsymbol{c}}_{t - 1}} + {\mathit{\boldsymbol{e}}_t}*{{\mathit{\boldsymbol{\hat c}}}_t}, \\ {\mathit{\boldsymbol{h}}_t} = {\mathit{\boldsymbol{o}}_t}*\tanh \left( {{\mathit{\boldsymbol{c}}_t}} \right). \end{array} $ | (5) |
式中:xt和ht分别为t时刻的输入与输出向量; Wa、We、Wo和Wc分别表示与之对应的门的权重矩阵和记忆状态权重矩阵; ba、be、bo和bc分别为对应的偏置向量; σ()是门单元的Sigmoid激活函数; tanh()是记忆状态的激活函数;*和·分别是Hadamard乘法和矩阵乘法。因为门单元引入,使门单元的输出限制在1以下,可以很好地避免梯度的爆炸增长问题,增加模型训练的稳定性。此外,门单元的引入使得长短期记忆神经网络的结构可以更长时间地保存过去的信息。
2.2 内容文件流行度预测模型在长短期记忆神经网络的基础上,本文提出一种3层堆叠的长短期记忆神经网络结构用于内容文件流行度预测。输入预测模型的内容文件流行度特征序列先后通过特征提取层、非线性映射层和流行度预测层,最后得到内容文件流行度预测模型的预测输出。因为内容文件的历史访问次数与内容文件未来流行度之间有较大的关联性[18],所以移动边缘网络中的每一个智能接入热点m每隔r小时,为每一个内容文件i∈F记录对应的请求次数pi(m, [t-r, t))。为了更好地运用数据和减少数值优化问题,本文对内容文件的历史请求次数做对数变换后作为预测模型的输入值,即
| $ x_{i}\left(m, t_{:} r\right)=\log \left(p_{i}(m, [t-r, t))+1\right). $ | (6) |
为了能够自适应地预测随时间不断变化的内容文件流行度,本文使用一个长度为R的滑动窗为每个内容文件i∈F保存时间最近的R个输入值。这R个输入值被组成内容文件流行度预测模型的输入特征序列。即,在tz时刻,内容文件流行度预测模型的输入特征序列可表示为xi(m, tz:r)=[xi(m, tz-r·(R-1):r),…,xi(m, tz:r)]。也就是说,内容文件流行度预测模型根据输入的特征序列xi(m, tz:r)预测内容文件i在未来时间间隔[tz, tz+1)内的流行度pi(m, [tz, tz+1))。
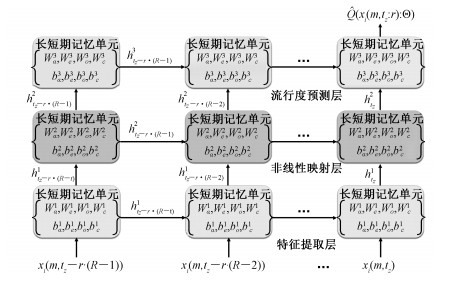
图 2展示本文所提内容文件流行度预测模型的结构。在输入层,输入特征序列xi(m, tz:r)中的R个值按时间顺序被先后输入到内容文件流行度预测模型。水平方向表示时间轴,每一层上的长短期记忆神经网络单元在不同时刻相互分享参数。3层不同作用的长短期记忆神经网络在垂直方向上堆叠,不同层的长短期记忆神经网络单元参数不同。低层长短期记忆神经网络的输出被直接作为高层长短期记忆神经网络的输入。最底层的长短期记忆神经网络用于提取输入特征序列的抽象特征,称为特征提取层。预测模型的输入序列是不同时刻经过对数变换的内容文件历史访问次数,这些不同时刻的历史访问次数与未来内容文件流行度的相关程度是不同的。我们利用特征提取层学习不同时刻历史访问次数与未来内容文件流行度的相关联程度,即学习输入特征序列的特征表示。第二层长短期记忆神经网络把第一层学习到的特征表示进一步进行非线性映射,组合成更加复杂的内容文件历史访问模式表示。我们称第二层长短期记忆神经网络为非线性映射层。在预测模型的最后一层(流行度预测层),内容文件历史访问模式表示被进一步映射表示成为内容文件未来流行度信息。
|
Download:
|
| 图 2 堆叠LSTM神经网络内容文件流行度预测模型 Fig. 2 Popularity prediction model via stacked LSTM | |
这种堆叠结构的长短期记忆神经网络每一层都有不同的作用。与单层的长短期记忆神经网络相比,堆叠的长短期记忆神经网络可以增加模型容量,学习到更加复杂的特征表示,由此提高内容文件流行度的预测准确性。在输出层,本文使用线性回归的方式预测时间间隔[tz, tz+1)内的内容文件受欢迎程度。堆叠长短期记忆神经网络内容文件流行度预测模型中不同层长短期记忆神经网络的维度从特征提取层到流行度预测层依次分别设定为:60, 120, 40。该堆叠长短期记忆神经网络整体的参数个数约为W=127000。此外,因为内容文件受欢迎程度的数值区间范围很大(大约为100~109),为避免数值优化问题,这里同样使用对数变换获得模型训练时对应的标签,即
| $ Q_{i}\left(m, \left[t_{z}, t_{z+1}\right)\right)=\log \left(p_{i}\left(m, \left[t_{z}, t_{z+1}\right)\right)+1\right). $ | (7) |
图 2预测模型中的参数可以通过解下面的优化问题(8)获得:
| $ \mathop {\min }\limits_\Theta \frac{1}{D}\sum\limits_{i = 1}^D l \left( {{Q_i}\left( {m, \left[ {{t_z}, {t_{z + 1}}} \right)} \right), \hat Q\left( {{x_i}\left( {m, {t_z};r} \right):\Theta } \right)} \right), $ | (8) |
式中:
求解优化问题(8)的过程就是本文所提的堆叠长短期记忆神经网络内容文件流行度预测模型的训练过程。对于深度神经网络,通常无法直接计算得到对应优化问题的全局最优解,但是优化目标函数对神经网络参数的导数可以求得。因此本文使用深度学习中最常使用的随机梯度下降法(stochastic gradient descent, SGD)和时间反向传播算法[19](back propagation through Time)对问题(8)迭代求解,逐步逼近最优解[17]。单次预测模型参数迭代更新的复杂度为Ο(W)[20],其中W为模型参数个数。因为本文所提的深度缓存策略采用离线训练的方式进行内容文件流行度预测模型,所以模型训练带来的时间消耗可忽略不记。
3 仿真实验 3.1 仿真设置本文使用从Facebook网站收集的真实视频数据集[13],数据集中包含总共1820个上传在Facebook网站的视频和其3个月间每个小时被访问的次数。根据实际情况下,午夜时刻移动网络通常处于通信量低谷期的事实,本文设置预测模型参数为:R=32,r=1,tz时刻到tz+1时刻的时间间隔为24h。即,移动边缘网络中的每一个智能接入热点每隔1h记录一次本地所有内容文件在此期间的被请求次数,每隔24h根据最新预测的本地内容文件未来流行度更新一次缓存内容。内容文件未来流行度预测结果由最近32h的内容文件历史请求特征序列通过本文提出的堆叠长短期记忆神经网络模型给出。移动边缘网络缓存系统这种运行方式一方面可以动态跟踪内容文件流行度的变化,从而提高系统的缓存命中率、提升用户体验;另一方面可以在移动边缘网络通信量的低谷时期进行缓存更新任务,从而减少对系统回传链路网络的负载、平衡通信量高峰期和低谷期之间的回传链路上的负载,提高系统效能。
此外,本文使用深度学习中经常使用的数据增强操作[21]。真实数据集先被分成训练数据集(820个视频)和测试数据集(1000个视频)。然后对训练数据集执行数据增强操作。对每一个训练样本,划分并选择5个相互不重叠的窗口,每个窗口中包含56h的数据,总共获得4100个训练样本(即D=4100)。在训练阶段,10折交叉验证技术被用于设置超参数。同时,Dropout技术[22]被应用在训练过程,用于防止预测模型的过拟合。我们连续在一个智能接入热点上仿真运行本文提出的移动边缘缓存策略7天。进而验证本文提出的基于深度学习的内容文件流行度预测模型的有效性和深度缓存策略在移动边缘缓存网络中的性能。
3.2 性能比较仿真实验首先对本文提出的基于深度学习的堆叠长短期记忆神经网络内容文件流行度预测方法和目前性能最优的流行度SVR(support vector regression)[13]预测方法进行比较。为了进一步验证本文提出的3层堆叠长短期记忆神经网络模型结构(简称:堆叠LSTM)的有效性,还与单层长短期记忆神经网络模型结构(简称:单层LSTM)进行了比较。内容文件流行度预测精确度对比结果如表 1所示。3种不同的预测方法得到的Spearman rank(斯皮尔曼等级)系数均值和95%置信区间如表 1所示。虽然流行度SVR方法通过核函数的应用,增加了模型的容量,已经得到了较高的预测精度。但是基于深度学习的循环神经网络框架的两种方法无论是从预测精确度还是预测鲁棒性的角度都超越了目前最优的流行度SVR预测方法。通过比较单层LSTM和堆叠LSTM两种基于深度学习的方法,发现堆叠LSTM结构给出了更高的预测精确度和预测稳定性。这意味着本文提出的3层不同作用的LSTM神经网络堆叠结构有效提高了模型对于内容文件流行度预测的表达能力。在仿真中注意到,如果要把流行度预测系统整合入缓存系统中,Spearman rank系数可能并不能很好地评价流行度预测系统对于缓存系统而言的优劣。针对本文提出的缓存系统,在表 1中比较了Top 50和Top 100两个指标。其中Top 50指标指的是流行度最高的50个视频中排列顺序正确的视频占比,依此类推。依据这两个指标,本文提出的基于深度学习的两种预测方法均优于流行度SVR预测方法。我们还发现,针对流行度预测这一任务,深度学习的损失函数可以进一步设计,而不是简单地使用MSE。通过进一步设计深度学习的损失函数,可以使模型能够更好应对流行度预测任务的需求。
|
|
表 1 内容文件流行度预测准确度比较 Table 1 File popularity prediction accuracy comparison |
在仿真实验中,我们测试了本文所提的堆叠长短期记忆神经网络内容文件流行度预测模型在执行模型预测时的时间消耗,并与流行度SVR方法进行比较,如表 2所示。虽然本文所提的神经网络预测模型从性能上优于流行SVR方法,但是因为该神经网络模型的规模不是很大,因此执行模型预测所需消耗的时间与流行度SVR方法相当。在实际系统中,神经网络预测模型和流行度SVR方法的预测复杂度与待预测内容文件个数F均成线性关系。与传统缓存算法相比,本文所提的基于流行度预测神经网络模型的深度缓存策略需要额外进行模型预测,但是执行模型预测的耗时并不是很大。本文所提的深度缓存策略仅在移动边缘网络运行的空闲时期进行缓存内容文件的部署,适当使用一些计算资源换取缓存系统更高的运行效率。
|
|
表 2 内容文件流行度预测耗时比较 Table 2 File popularity prediction time cost comparison |
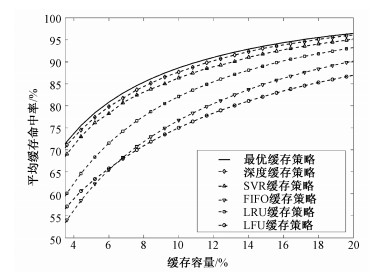
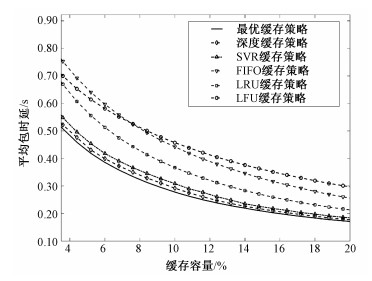
仿真实验还比较了本文提出的深度缓存策略与下列其他缓存策略,用于进一步验证基于堆叠长短期记忆神经网络结构预测模型设计的深度缓存系统的有效性。其中前3种是传统的缓存策略,SVR缓存策略是基于目前性能最佳的流行度SVR预测方法的缓存策略。具体如下:1)先入先出(first in first out, FIFO)缓存策略[23];2)最久使用(LRU)缓存策略[6];3)频率最少(LFU)缓存策略[7];4)流行度SVR缓存策略(简称:SVR缓存策略):流行度SVR这个预测方法被集成到本文的缓存系统中,代替本文提出的基于深度学习的预测方法;5)最优缓存策略:最优缓存策略使用真实系统无法得知的内容文件未来流行度信息进行缓存决策,是缓存系统能达到的最优性能。平均缓存命中率性能比较结果如图 3所示,平均包时延性能比较结果如图 4所示。
|
Download:
|
| 图 3 平均缓存命中率性能比较图 Fig. 3 Average cache hit rate comparison | |
|
Download:
|
| 图 4 平均包时延性能比较图 Fig. 4 Average packet delay comparison | |
我们使用与文献[24]相同的通信系统参数进行包时延性能仿真。缓存容量被定义为缓存文件数相对于文件库中文件数总数的占比。如图 3、图 4, 在所有缓存容量上,本文提出的深度缓存策略性能不仅优于传统的缓存策略还优于基于目前最优内容文件流行度预测方法的缓存策略。相比于传统缓存策略,本文提出的深度缓存策略有很大的性能提升。例如:当需要80%的平均缓存命中时,传统缓存策略中最好的LRU缓存策略与本文提出的深度缓存略差相比还需要额外50%的缓存容量;当缓存容量较小时,平均包时延可以降低约40%。传统缓存算法虽然也有考虑历史内容文件流行度信息,如LFU、LRU,但是这些缓存算法无法充分利用这些有限的历史流行度信息来预测内容文件未来的流行度。LFU很容易一直缓存过去点击次数非常多的内容文件,造成历史信息污染。LRU算法则会因一些偶发性的,周期性的内容文件需求而引发缓存污染。
本文提出的基于深度学习的内容文件流行度预测方法借助于深度神经网络强大的模式表示能力,学习到历史数据中不同增长、衰减方式的内容文件流行度变化的趋势。滑动窗的设计使得深度缓存策略可以实时跟踪内容文件历史流行度信息,从而动态地跟踪本地内容文件的流行度变化。仿真实验证明,把内容文件未来流行度信息考虑到缓存策略的制定中有助于提升缓存系统的性能,特别是遇到缓存容量因为硬件原因受到限制的情况时。深度学习方法的引入使得内容文件未来流行度的预测可以更加精确,进一步提升移动边缘缓存系统的性能。此外,与最优缓存策略比较发现,深度缓存策略的性能已经达到近似最优。
4 结论本文基于深度学习提出一种内容文件流行度预测方法,并依此设计一个最大化缓存命中率的深度缓存策略。因为本文提出的堆叠长短期记忆神经网络可以很好地发掘内容文件历史访问模式和内容文件未来流行度之间隐藏的关系,所以本文的内容文件流行度预测方法可以精确地预测内容文件未来的流行度。来自Facebook真实的视频数据集被用来验证本文提出的内容文件流行度预测方法和基于此的深度缓存策略。仿真结果证明本文提出的内容文件流行度预测方法性能优于目前最优的流行度SVR方法。依靠精准的内容文件流行度预测信息,本文提出的深度缓存策略的性能远超传统缓存策略,达到近似最优。
| [1] |
Bi S Z, Zhang R, Ding Z, et al. Wireless communications in the era of big data[J]. IEEE Communications Magazine, 2015, 53(10): 190-199. Doi:10.1109/MCOM.2015.7295483 |
| [2] |
CISCO, Inc. Cisco visual networking index: global mobile data traffic forecast[R/OL]. (2017-02)[2018-10-20]. https://www.cisco.com/c/en/us/soltions/collateral/service-provider/visual-networking-index-vni/mobile-white-paper-c11-520862.html.
|
| [3] |
Maddah M, Niesen U. Fundamental limits of caching[J]. IEEE Transactions on Infromation Theory, 2014, 60(5): 2856-2867. Doi:10.1109/TIT.2014.2306938 |
| [4] |
Bastug E, Bennis M, Debbah M. Living on the edge:the role of proactive caching in 5g wireless networks[J]. IEEE Communications Magazine, 2014, 52(8): 82-89. Doi:10.1109/MCOM.2014.6871674 |
| [5] |
余江, 邱玲. 密集小站网络下基于协作滤波的缓存内容决策和用户归属[J]. 中国科学院大学学报, 2016, 33(6): 802-807. |
| [6] |
Mohamed A, Traverso S, Giaccone P, et al. Analyzing the performance of lru caches under non-stationary traffic patterns[J]. ArXiv Preprint, 2013, 1301.4909. |
| [7] |
Jaleel A, Theobald K, Steely S, et al. High performance cache replacement using re-reference interval prediction (RRIP)[C]//ACM SIGARCH Computer Architecture News. New York: ACM, 2010: 60-71.
|
| [8] |
Müller S, Atan O, Schaar M, et al. Context-aware proactive content caching with service differentiation in wireless networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(2): 1024-1036. Doi:10.1109/TWC.2016.2636139 |
| [9] |
Li S H, Xu J, Schaar M, et al. Trend-aware video caching through online learning[J]. IEEE Transactions on Multimedia, 2016, 18(12): 2503-2516. Doi:10.1109/TMM.2016.2596042 |
| [10] |
Azimi S, Simeone O, Sengupta A, et al. Online edge caching and wireless delivery in fog-aided networks with dynamic content popularity[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(6): 1189-1202. Doi:10.1109/JSAC.2018.2844961 |
| [11] |
Somuyiwa S, György A, Gündüz D. A reinforcement-learning approach to proactive caching in wireless networks[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(6): 1331-1344. Doi:10.1109/JSAC.2018.2844985 |
| [12] |
Szabo G, Huberman B. Predicting the popularity of online content[J]. Communications of the ACM, 2010, 53(8): 80-88. Doi:10.1145/1787234.1787254 |
| [13] |
Trzciński T, Rokita P. Predicting popularity of online videos using support vector regression[J]. IEEE Transactions on Multimedia, 2017, 19(11): 2561-2570. Doi:10.1109/TMM.2017.2695439 |
| [14] |
Wang X F, Han Y W, Wang C Y, et al. In-Edge AI:intelligentizing mobile edge computing caching and communication by federated learning[J]. ArXiv Preprint, 2018, 1809. |
| [15] |
Lei L, You L, Dai G Y, et al. A deep learning approach for optimizing content delivering in cache-enabled HetNet[C]//Wireless Communication Systems (ISWCS), 2017 International Symposium on. Bologna: IEEE, 2017: 449-453.
|
| [16] |
Martello S, Pisinger D, Toth P. New trends in exact algorithms for the 0~1 Knapsack problem[J]. European Journal of Operational Research, 2000, 123(2): 325-332. Doi:10.1016/S0377-2217(99)00260-X |
| [17] |
Ma N, Tian G D, Zhou X. A lip-reading recognition approach based on long short-term memory[J]. Journal of University of Chinese Academy of Sciences, 2018, 35(1): 109-117. |
| [18] |
Friedman J, Hastie T, Tibshirani R. The elements of statistical learning[M]. New York: Springer Series in Statistics, 2001.
|
| [19] |
Werbos P.J. Backpropagation through time:what it does and how to do it[J]. IEEE Proceedings, 1990, 78(10): 1550-1560. Doi:10.1109/5.58337 |
| [20] |
Sak H, Senior A, Beaufays F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling[C]//Fifteenth annual Conference of the International Speech Communication Association. Singapore: ISCA Archive, 2014: 338-342.
|
| [21] |
Goodfellow I, Bengio Y, Courville A, et al. Deep learning[M]. Cambridge: MIT press, 2016.
|
| [22] |
Srivastava N, Hinton G, Krizhevsky A, et al. Dropout:a simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15(1): 1929-1958. |
| [23] |
Rossi D, Rossini G. Caching performance of content centric networks under multi-path routing[J]. Relatório técnico, Telecom ParisTech, 2011, 1-6. |
| [24] |
Amer R, Butt M, Bennis M, et al. Delay analysis for wireless D2D caching with inter-cluster cooperation[C]//2017 IEEE Global Communications Conference (GLOBECOM). Sigapore: IEEE, 2017: 1-7.
|
 2020, Vol. 37
2020, Vol. 37 


