不同于传统的基于循环前缀的正交频分复用(cyclic prefix-orthogonal frequency division multiple-xing, CP-OFDM)技术，第五代移动通信系统(the 5th generation mobile communication system, 5G)的新波形技术需要达到以下设计目标：频谱集中、时域拖尾较小、支持灵活的系统参数部署等。滤波正交频分复用(filtered-orthogonal frequency division multiplexing, Filtered-OFDM)是华为公司提出的一种面向5G的新波形技术，根据不同场景的需求，子带滤波器分别对每个子带进行滤波，不同子带可以根据相应的链路特性和用户需求调整系统参数^[1-2]。为能够适应5G新波形的要求，子带滤波器的设计对Filtered-OFDM系统非常重要。具体地，子带滤波器一般采用有限长单位冲激响应(finite impulse response, FIR)滤波器，且其设计需要满足以下5条准则^[3-5]：1)子带滤波器阻带衰减尽可能大，以降低相邻子带间干扰(inter-subband interference, IBI)，支持子带间非同步传输; 2)子带滤波器过渡带尽可能窄，以减小子带间的保护带宽(guard band)，从而提高频谱利用率; 3)子带滤波器的时域冲激响应拖尾尽可能小，以降低符号间干扰(inter-symbol interference, ISI)，更好地支持低时延业务; 4)子带滤波器通带波纹尽可能小，以降低滤波后所带来的频率选择性失真; 5)为了实现灵活的带宽分配，子带滤波器需易于实现。

FIR滤波器主要有4种设计方法：窗函数法、迭代优化法^[6-9]、等波纹法^[1-10]和频域抽样法^[11]。从实现复杂度与易用性方面考虑，目前，基于Filtered-OFDM系统的子带滤波器主要采用窗函数法^{[1-5, 12-15]}，即先设计满足目标频率响应的线性相位滤波器，然后用窗函数软截断其时域冲激响应得到子带滤波器。目前，对于基于窗函数法的FIR子带滤波器，研究者一般对窗函数进行设计优化^[16-20]，或者优化滤波实现过程^[21-23]，就笔者所知，鲜有人从线性相位滤波器角度出发进行研究。目前，线性相位滤波器主要有理想低通滤波器和升余弦滤波器，对应的子带滤波器分别为软截断SinC型子带滤波器(SinC-filter)^{[1-5, 12-13]}和软截断升余弦子带滤波器RC-Filter(raised-cosine filter)^[14-15]。SinC-Filter的线性相位滤波器为理想低通，由于其通带边缘由1直接过渡到0，导致SinC-Filter的时域色散严重，且通带波纹较大; RC-filter的线性相位滤波器为升余弦函数，由于升余弦函数的滚降带受制于子带带宽和滚降系数，导致RC-Filter的滤波器参数配置不灵活; 且由于RC-Filter的线性相位滤波器通带边缘由1缓慢过渡并接近于0，使得滚降频带过宽，导致RC-Filter的过渡带较宽。

本文设计一种缩短型-修正软截断升余弦子带滤波器(TMRC-Filter，truncate modified raised-cosine filter)。与SinC-Filter和RC-Filter相比，TMRC-Filter的线性相位滤波器的滚降带宽可通过所设计的截止幅度参数自由调节，进而其频域响应更为灵活，时域色散程度更小。仿真结果表明，随着滚降带宽的增大，TMRC-Filter的阻带衰减、过渡带带宽增大，时域色散程度减小。通过对TMRC-Filter的滚降带宽和滚降系数进行调节，TMRC-Filter可实现较大的阻带衰减、较小的时域色散程度、较窄的过渡带和较小的通带波纹系数。仿真结果进一步表明，当窗函数使用汉宁窗，滚降带宽取0.0106π时，TMRC-Filter的通带波纹可达10^-3dB量级，其时域色散程度相比于SinC-Filter改善75%，且在期望阻带衰减大于等于-60dB的性能需求下，TMRC-Filter较RC-Filter有超过7%的带宽改进率。将TMRC-Filter与一种迭代优化法所实现的滤波器^[8]进行对比，其性能与文献[8]中滤波器的性能相当，但是文献[8]中滤波器会出现生成滤波器的截止频率不能收敛到目标截止频率的情况，因此需要进行多步迭代操作，而TMRC-Filter只需将线性相位滤波器和窗函数的时域形式进行相乘便可获得，无需多次迭代，实现较为简单。

1 基于窗函数法的子带滤波器设计

窗函数法^[3]子带滤波器设计分为两步，第1步设计满足目标频率响应的线性相位滤波器F_d(ω)，并得到其时域冲激响应f_d(n)，第2步选择合适的窗函数w(n)软截断f_d(n)得到子带滤波器。本节将提出带有通带边缘截止幅度的TMRC-Filter。首先分析传统SinC-Filter和RC-Filter的线性相位滤波器的不足，进而提出可自由调节滚降带宽的带有通带边缘截止幅度的线性相位滤波器，并进行时域色散度分析; 然后分析窗函数软截断生成TMRC-Filter的过程; 最后提出预留频带$ \partial B$的设置方法。

1.1 线性相位滤波器设计

传统的采用窗函数法的子带滤波器设计中，线性相位滤波器设计一般基于SinC函数或升余弦函数：

a) 对基于SinC函数的滤波器SinC-Filter，其线性相位滤波器的频域表达式为

$ {F_{\rm{d}}}\left( \omega \right) = \left\{ {\begin{array}{*{20}{c}} 1&{0 \le \left| \omega \right| \le B + \partial B}\\ 0&{B + \partial B < \left| \omega \right| \le {\rm{ \mathsf{ π} }}} \end{array}} \right., $

(1)

b) 对基于升余弦函数的滤波器RC-Filter，其线性相位滤波器的频域表达式为

$ {F_{\rm{d}}}\left( \omega \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le \left| \omega \right| < B + \partial B\\ 0.5\left( {1 + \sin \left( {\frac{{\rm{ \mathsf{ π} }}}{{2\alpha }}\left( {1 - \frac{{1 - \alpha }}{{\tau B}}\left| \omega \right|} \right)} \right)} \right),\;\;\;\;B + \partial B \le \left| \omega \right| \le B + \partial B + \Delta ,\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;B + \partial B + \Delta < \left| \omega \right| \le {\rm{ \mathsf{ π} }} \end{array} \right. $

(2)

式中：B表示子带带宽，$\partial B $表示预留频带(tone-offset)，Δ表示滚降带宽，α表示滚降系数，ω表示频率。

窗函数与线性相位滤波器卷积后，会产生吉布斯(Gibbs)现象，即在通带内产生波纹。为了避免通带波纹对边缘子载波的影响，在设计线性相位滤波器时，设置预留频带$\partial B $对子带带宽进行预增大^{[3, 13]}。预留频带$\partial B $一般设置为2~12个子载波，若设置过小，不能完全避免子带滤波器的通带波纹对边缘子载波的影响; 设置过大，则导致从子带滤波器的通带截止频率处到所期望的阻带衰减处的过渡区域变大^[24]。对于线性相位滤波器(1)，其通带边缘由1直接过渡到0，导致子带滤波器的时域色散度较高，通带波纹较大。对于线性相位滤波器(2)，滚降带宽$\Delta=\frac{2 \alpha}{1-\alpha}(B+\partial B) $，由于滚降带宽Δ是B与α的函数，导致RC-Filter的滤波器参数配置不灵活，且此时线性相位滤波器通带边缘由1缓慢过渡到0，滚降带过宽且不易控制。

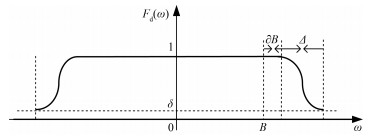
综上，如图 1所示，设计满足目标频率响应的可自由调节滚降带宽的带有通带边缘截止幅度δ的线性相位滤波器：

$ {F_{\rm{d}}}\left( \omega \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le \left| \omega \right| < B + \partial B\\ x\left( {\left| \omega \right|,\alpha ,B} \right),B + \partial B \le \left| \omega \right| < \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;B + \partial B + \Delta \\ \delta ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| \omega \right| = B + \partial B + \Delta \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;B + \partial B + \Delta < \left| \omega \right| \le {\rm{ \mathsf{ π} }} \end{array} \right. $

(3)

相比于线性相位滤波器(1)和(2)中的预留频带$\partial B $，所设计的线性相位滤波器(3)中$\partial B $不再由经验值设置，而是可以进行确定性设置，设置方法见1.4节，从而可以避免预留频带$\partial B $设置过大或者过小带来的性能损失问题。x(|ω|, α, B)表示滚降函数，为便于与RC-Filter和SinC-Filter进行对比分析，此处滚降函数取为升余弦函数，即

$ x\left( {\left| \omega \right|,\alpha ,B} \right) = 0.5\left( {1 + \cos \left( {\frac{{B + \partial B - \left| \omega \right|}}{\alpha }} \right)} \right), $

(4)

式中：Δ表示滚降带宽，可以自由调节。与RC-Filter的线性相位滤波器(2)不同的是，线性相位滤波器(3)的滚降带宽Δ不再由B和α决定，而是可以自由调节; $ \delta=x(|B+\partial B+\mathit{\Delta}|)$表示截止幅度，受滚降带宽Δ控制，可以通过调节滚降带宽Δ来调节截止幅度δ，特别地，当Δ=0时，δ=1，此时线性相位滤波器(3)与(1)等价; 当Δ=απ时，δ=0，此时线性相位滤波器(3)与(2)等价。线性相位滤波器(3)的时域冲激响应为

$ \begin{array}{l} {f_{\rm{d}}}\left( n \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \left( {B + \partial B + \Delta } \right)}^{B + \partial B + \Delta } {{F_{\rm{d}}}} \left( \omega \right){{\rm{e}}^{{\rm{j}}\omega n}}{\rm{d}}\omega \\ \;\;\;\;\;\;\;\;\; = \left( {B + \partial B + \Delta } \right) \sin c \left( {B + \partial B + \Delta } \right)n + \\ \;\;\;\;\;\;\;\;\;\left( {B + \partial B} \right)\sin c\left( {\left( {B + \partial B} \right)n} \right) + \\ \frac{{\sin \left( {\left( {B + \partial B + \Delta } \right)n - \frac{\Delta }{\alpha }} \right) - \sin \left( {\left( {B + \partial B} \right)n} \right)}}{{2\left( {n - \frac{1}{\alpha }} \right)}} + \\ \frac{{\sin \left( {\left( {B + \partial B + \Delta } \right)n + \frac{\Delta }{\alpha }} \right) - \sin \left( {\left( {B + \partial B} \right)n} \right)}}{{2\left( {n + \frac{1}{\alpha }} \right)}}. \end{array} $

(5)

1.2 线性相位滤波器的时域色散度分析

由文献[25]可知，可以用Δn来衡量滤波器能量在时间上的散布情况：

$ \begin{array}{l} \Delta n = \sqrt {\sum\limits_{n = - \infty }^{ + \infty } {{{\left( {n - \bar n} \right)}^2}} {{\left| {{f_{\rm{d}}}\left( n \right)} \right|}^2}} \\ \bar n = \sum\limits_{n = - \infty }^\infty n {\left| {{f_{\rm{d}}}\left( n \right)} \right|^2}. \end{array} $

(6)

式中：$ {\bar n}$为滤波器在时间轴上能量分布的中心值，Δn表示滤波器在时域的色散值，描述滤波器的能量在时间轴上的散布情况。由式(6)可知，Δn越小，滤波器在时间轴上能量越集中。

由于f_d(n)关于n=0对称，所以$ {\bar n}$=0，则得

$ \Delta n = \sqrt {2\sum\limits_{n = 0}^\infty {{n^2}} {{\left| {{f_{\rm{d}}}\left( n \right)} \right|}^2}} . $

(7)

为评估滚降带宽Δ对时域色散值Δn的改善程度，定义参数η_Δn

$ {\eta _{\Delta n}}\left( \Delta \right) = \frac{{\Delta n\left( 0 \right) - \Delta n\left( \Delta \right)}}{{\Delta n\left( 0 \right)}}. $

(8)

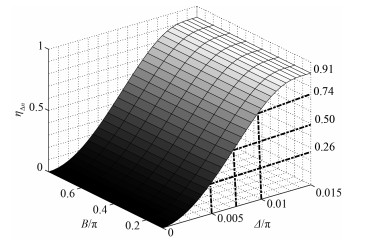
取α=0.015，η_Δn随滚降带宽Δ和子带带宽B的变化如图 2所示。

由图 2可知，η_Δn随着滚降带宽Δ的增加而增加，当Δ∈[0.01π, 0.015 π]时，η_Δn增加较为缓慢，且η_Δn(Δ)不受子带带宽B影响。

1.3 软截断生成TMRC-Filter

根据窗函数法^[3]，由合适的窗函数w(n)软截断线性相位滤波器(3)的时域冲激响应f_d(n)得到TMRC-Filter f(n)，即

$ f\left( n \right) = {f_{\rm{d}}}\left( n \right)w\left( n \right),0 \le n \le L - 1, $

(9)

式中：L为滤波器的阶数，可选择的窗函数w(n)有汉宁窗、布莱克曼窗、凯泽窗、哈明窗等^[14-18]。

TMRC-Filter的幅度响应为

$ \begin{array}{l} H\left( \omega \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}{F_{\rm{d}}}\left( \omega \right) * W\left( \omega \right)\\ \;\;\;\;\;\;\;\;\; = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \left( {B + \partial B + \Delta } \right)}^{B + \partial B + \Delta } {{F_{\rm{d}}}} \left( \theta \right)W\left( {\omega - \theta } \right){\rm{d}}\theta \\ \;\;\;\;\;\;\;\;\; = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \left( {B + \partial B} \right)}^{B + \partial B} {W\left( {\omega - \theta } \right){\rm{d}}\theta } + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \left( {B + \partial B + \Delta } \right)}^{ - \left( {B + \partial B} \right)} x \left( \theta \right)W\left( {\omega - \theta } \right){\rm{d}}\theta + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \left( {B + \partial B} \right)}^{B + \partial B + \Delta } x \left( \theta \right)W\left( {\omega - \theta } \right){\rm{d}}\theta + \\ \;\;\;\;\;\;\;\;\; = S\left( \omega \right) + R\left( \omega \right), \end{array} $

(10)

其中，W(ω)是窗函数的幅度响应

$ \begin{array}{*{20}{c}} {\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \left( {B + \partial B} \right)}^{B + \partial B} {W\left( {\omega - \theta } \right){\rm{d}}\theta } ;}\\ {R\left( \omega \right) = {R_0}\left( {B + \partial B + \omega } \right);}\\ {{R_0}\left( \omega \right) = \int_{ - \Delta }^0 0 .5\left( {1 + \cos \left( {\frac{\theta }{\alpha }} \right)} \right)W\left( {\theta + \omega } \right){\rm{d}}\theta + }\\ {\int_0^\Delta 0 .5\left( {1 + \cos \left( {\frac{{ - \theta }}{\alpha }} \right)} \right)W\left( {\theta - \omega } \right){\rm{d}}\theta .} \end{array} $

(11)

由式(10)、式(11)可知，TMRC-Filter幅度响应可以表示为S(ω)和R(ω)的和; 其中S(ω)等价于SinC函数子带滤波器的幅度响应，R(ω)等价于滚降函数与窗函数的卷积结果，对SinC函数子带滤波器的幅度特性S(ω)进行修正，从而降低TMRC-Filter的通带波纹系数，增大阻带衰减。由于增加了滚降带宽Δ，相比于SinC函数子带滤波器，TMRC-Filter的过渡带增大，因此，Δ不可设置过大。

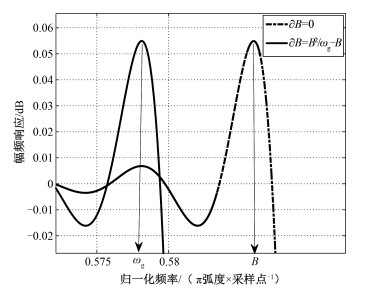
1.4 预留频带设置方法

预留频带$ \partial B$ =0和预留频带$ \partial B$≠0两种情况下的线性相位滤波器与窗函数卷积后生成的子带滤波器的幅度响应如图 3所示。由图 1可知，当$ \partial B$=0时，线性相位滤波器的通带截止频率为B，线性相位滤波器与窗函数卷积后生成的子带滤波器的幅度响应如图 3实线所示，子带滤波器的通带边缘处最后一个正肩峰G所对应的频率为ω_g，但为了既节省频带资源又避免通带波纹对边缘子载波的影响，子带滤波器的通带边缘最后一个正肩峰应尽量出现在B处，如图 3虚线所示，因此$ \partial B$的设置保证子带滤波器通带边缘处的最后一个正肩峰G所对应的的频率为B，则此时线性相位滤波器的通带截止频率$ B + \partial B$必须满足

$ \frac{B}{{{\omega _{\rm{g}}}}} = \frac{{B + \partial B}}{B}, $

(12)

即

$ \partial B = \frac{{{B^2}}}{{{\omega _{\rm{g}}}}} - B. $

(13)

本章设计可自由调节滚降带宽的带有通带边缘截止幅度的线性相位滤波器，用窗函数软截断该线性相位滤波器的时域冲激响应生成TMRC-Filter，并提出预留频带$ \partial B$的设置方法。

2 仿真分析

滤波器的技术指标主要有通带截止频率、阻带截止频率、阻带衰减、过渡带带宽以及通带波纹，为便于对TMRC-Filter进行性能仿真分析，对技术指标定义见表 1。

本文将TRMC-Filter与SinC-Filter，RC-Filter进行对比。为了增加所设计线性相位滤波器的普适性，仿真中改变不同的窗函数进行分析。本仿真实验设置仿真参数见表 2。

2.1 TMRC-Filter的通带波纹和阻带衰减

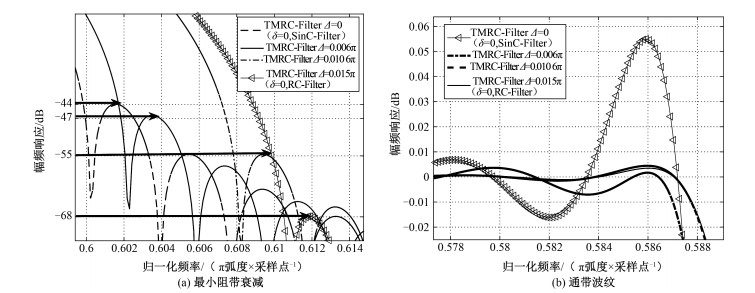
以汉宁窗函数为例，取α=0.015，由式(13)得到TMRC-Filter(Δ=0, δ=1)、TMRC-Filter(Δ=0.006 π, δ=0.6545)、TMRC-Filter(Δ=0.010 6π, δ=0.1977)、TMRC-Filter (Δ=0.015π, δ=0)的预留频带$ \partial B$分别为0.0135B、0.00665B、0.0094B、0.0094B。不同Δ下，TMRC-Filter幅度响应如图 4所示，其相应的通带波纹系数和最小阻带衰减如表 3所示。其中，当Δ=0时，δ=1，此时TMRC-Filter与SinC-Filter等价; 当Δ=απ=0.015 π时，δ=0，此时TMRC-Filter与RC-Filter等价。

由表 3和图 4(a)可知，当Δ取值0、0.006π、0.0106π、0.015π时，TMRC-Filter最小阻带衰减A_s分别为-44、-47、-55、-68 dB，即TMRC-Filter的最小阻带衰减幅度随着Δ的增大而变大，与RC-Filter，SinC-Filter相比，TMRC-Filter的最小阻带衰减幅度处于两者之间; Δ越小，TMRC-Filter的过渡带带宽度越小，且TMRC-Filter的过渡带带宽度小于RC-Filter的过渡带带宽度。

由表 3和图 4(b)可知，TMRC-Filter和RC-Filter的通带波纹达到10^-3量级，明显小于SinC-Filter的通带波纹值。

由表 3和图 4的结果分析可知，Δ的存在显著降低了通带波纹系数。通过Δ的调节，可自由调节滤波器的阻带衰减和过渡带带宽。Δ的取值有两个要求：Δ应尽可能小以获得较窄的过渡带; Δ又应尽可能大以获得较小的时域色散值和较大的阻带衰减。因此，这两个要求是相互矛盾的，不可能同时满足。Δ的取值应该在较窄的过渡带、较小的时域色散度及较大的阻带衰减之间进行折衷。由2.2节图 2可知，当Δ=0.0106π时，η_Δn=0.75，相比于SinC-Filter，TMRC-Filter时域色散度改善较大，并结合图 4(a)可知其通波纹系数较小，阻带衰减较大，且相比于RC-Filter，其过渡带带宽较小。

2.2 TMRC-Filter的过渡带

以汉宁窗函数为例，取α=0.015, Δ=0.0106π，不同期望阻带衰减A_g下，3种子带滤波器的期望过渡带带宽U见表 4。

由表 4可知，当期望阻带衰减A_g大于等于-60dB时，3个滤波器的过渡带带宽度关系为U_RC>U_TMRC>U_SinC，此时TMRC-Filter的过渡带U_TMRC较RC-Filter有较大的改进，定义滤波器的带宽改进率为

$ {\eta _U} = \frac{{{U_{{\rm{RC}}}} - {U_{{\rm{TMRC}}}}}}{{{U_{{\rm{RC}}}}}}. $

(14)

不同参数下的TMRC-Filter的带宽改进率如表 5所示。

由表 5可知，当期望阻带衰减大于等于-60dB时，TMRC-Filter较RC-Filter有超过7%的带宽改进率。但相比于SinC-Filter，TMRC-Filter的过渡带宽度仍然较宽。

2.3 改变不同的窗函数进行性能分析

当窗函数为文献[16]所提出的窗函数时，不同子带滤波器的性能指标见表 6(其中，☆表示滤波器性能达不到要求)。

由表 6可知，此窗函数下，TMRC-Filter、RC-Filter和SinC-Filter 3种滤波器的通带波纹相当; TMRC-Filter和RC-Filter的最小阻带衰减明显大于SinC-Filter，且当期望阻带衰减小于等于-85dB时，SinC-Filter已失去其过渡带较窄的优势; 当期望阻带衰减大于等于-94dB时，3个滤波器的过渡带关系为U_RC>U_TMRC>U_Sinc，此时TMRC-Filter的过渡带U_TMRC较RC-Filter有较大的改进，利用公式(14)，计算其带宽改进率见表 7，可以看出，当期望阻带衰减大于等于-94 dB时，TMRC-Filter较RC-Filter超过7%的带宽改进率。当期望阻带衰减大于等于-80 dB时，TMRC-Filter的过渡带宽度略大于SinC-Filter。因此当Filtered-OFDM系统对带外辐射要求不高时，SinC-Filter整体性能较好; 当系统对带外辐射要求较高时，TMRC-Filter更能满足性能需求。

2.4 误码率分析

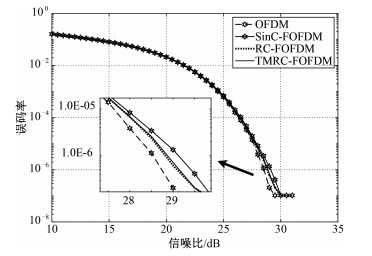
使用滤波器对子带进行滤波，其中，TMRC-FOFDM使用TMRC-Filter对子带进行滤波，RC-FOFDM使用RC-Filter对子带进行滤波，SinC-FOFDM使用SinC-Filter对子带进行滤波。将滤波后的发送信号经过高斯信道，得到其对应的误码率(bit error rate, BER)见图 5。

由图 5可知，TMRC-FOFDM、RC-FOFDM误码率近似，且接近于传统的OFDM的误码率，说明所设计的滤波器对信号未造成明显的失真。对于高信噪比下，TMRC-FOFDM、RC-FOFDM相比于SinC-FOFDM误码率较小，说明带有滚降带的子带滤波器TMRC-Filter、RC-Filter的通带波纹小于SinC-Filter的通带波纹。

2.5 与其他FIR滤波器对比分析

为体现所设计滤波器优势，本节将对TMRC-Filter和文献[8]所提出FIR滤波器的性能进行对比分析。文献[8]所设计的滤波器为基于高斯函数近似(Gaussian-based approximation, GBA)的迭代滤波器，该滤波器易于实现，且可控制过渡带带宽，本文将该滤波器命名为GBA-Based-Filter。

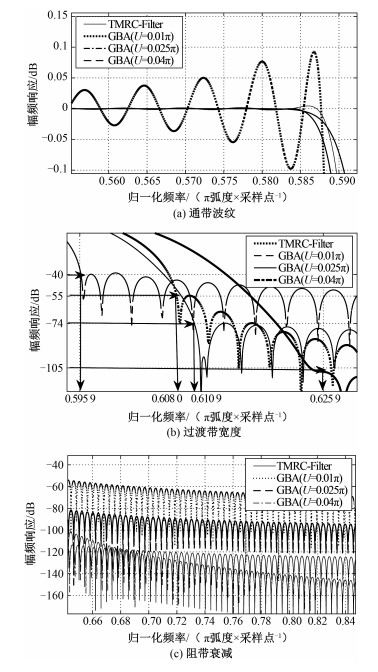
仿真实验子带带宽为0.5859π，滤波器长度为513。对于TMRC-Filter，其滚降带宽Δ=0.0106π，对应的截止幅度为δ=0.1977，滚降系数α=0.015;由于GBA-Based-Filter是通过优化过渡带带宽度来进行迭代实现，因此不同过渡带带宽的滤波器性能不同，取目标过渡带带宽度分别为0.01π、0.025π、0.04π，得到与TMRC-Filter的性能对比结果分别如图 6所示。

由图 6可知，当GBA-Based-Filter的过渡带带宽优化到0.01π时，虽然其过渡带带宽窄于TMRC-Filter，但其性能在通带波纹和阻带衰减方面均差于TMRC-Filter; 当GBA-Based-Filter的过渡带带宽优化到0.025 π时，其过渡带带宽和TMRC-Filter相似，虽然其通带波纹略优于TMRC-Filter，但其阻带衰减略差于TMRC-Filter; 当GBA-Based-Filter的过渡带带宽优化到0.04π时，虽然其性能在通带波纹方面略优于TMRC-Filter，但过渡带带宽较宽，且两种滤波器在阻带衰减方面性能相当。

3 总结

本文针对Filtered OFDM系统设计一种子带滤波器。为满足Filtered OFDM系统对带宽分配灵活、较高时频效率以及非同步传输的要求，所设计的子带滤波器可通过调节滚降带宽，实现较大的阻带衰减、较窄的过渡带带宽、较小的通带波纹以及较大的时域色散程度，且实现较为简单。但本文并未给出滚降带宽与4个性能指标的理论数学关系，因此，推导出滚降带宽与4个性能指标的闭合表达式是接下来要进行的工作。