2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
激光雷达因具有方向性好、测距精度高等特点,在深空探测和地球科学领域中彰显了巨大的应用潜力,逐渐成为快速获取高精度地形数据的重要技术手段[1-2]。2016年5月发射的资源三号02星首次搭载中国自行研制的对地观测试验性载荷激光测高仪,在后续的高分7号、陆地生态系统碳卫星也都计划搭载激光测高仪[3]。由此可见,激光测高技术已经进入快速发展时期。在星载激光测高仪研制与测试过程中,经实验室标定后仪器一般具有很高的指向和测距精度。但由于卫星发射时的振动以及入轨后空间环境的变化等因素影响,测高仪的指向、测距等系统定标参数相对于发射前地面测量值会发生变化,从而引起激光的平面和高程误差[4-5]。以轨道高度约为505km的资源三号02星激光测高仪为例,在地表入射角为1°时,30″的激光指向误差引起足印定位水平误差76m,高度误差1.3m。因此,对于高精度激光测高数据,通过在轨几何定标方法消除其主要的系统误差就显得尤为重要。
在资源三号02星之前,美国ICESat卫星搭载了对地激光测高仪GLAS系统。针对GLAS的在轨几何定标方法,国内外的研究人员在ICESat卫星发射前后开展了不少相关研究工作,主要可以分为基于自然地形定标法和地面实时探测定标法[6-11]。自然地形定标法需要卫星进行姿态机动或者分析波形数据与已知地形进行对比计算定标参数。资源三号02星只具备整星横滚侧摆能力,姿态机动能力弱,且测距系统只提供测距信息不下传波形数据,因此无法利用此类方法进行定标[3-4]。地面实时探测定标法需要在室外布设大量探测器捕捉激光能量信号以确定激光足印控制点的精确位置,根据激光足印原始坐标与控制点坐标的差异计算定标参数。2016年8月中旬到9月上旬,国家测绘地理信息局牵头组织了百余名工程技术人员,在内蒙古自治区采用地面实时探测定标法,进行资源三号02星测高仪在轨几何定标试验,并取得圆满成功[12]。基于地面实时探测定标法定标精度及可靠性较高,但试验难度大,定标场地的建设要求苛刻,需耗费大量时间人力物力。因此有专家学者提出星载激光测高仪无场定标技术的设想[13],即在不需要布设探测器定标场地的情况下实现对激光测高仪的几何定标,以降低定标的时间消耗及成本。在测高仪无场几何定标方面,唐新明等[14]提出基于金字塔地形匹配预估ZY3-02星测高仪的指向角,为后续的地面探测器定标试验的实施提供支撑;张过等[13]利用已知地形数据与初始测高值匹配进行ZY3-02星测高仪初射方向的初步定标,能够比较准确地确定激光足印点的位置坐标,为建立激光几何定标场提供依据。
本文在充分研究现有星载激光测高仪定标方法的基础上,探索一种无需布设野外定标场地的测高仪在轨几何定标方法,实现其姿态及测距误差的校正。首先基于星载激光测高仪足印定位几何模型,并结合系统误差分析推导测高仪几何定标模型;然后详细介绍基于曲线匹配的测高仪无场在轨几何定标方法;最后使用资源三号02星原始激光测高数据对定标方法进行验证,通过选取多轨测高数据进行定标前后高程精度的评估。实验数据分析表明,测高数据经过本文的定标方法校正后高程精度取得显著提升,验证了此方法的有效性。
1 激光测高仪无场在轨几何定标方法 1.1 几何定标模型构建星载激光测高系统的工作是由多个子系统协同完成的,其中激光测距仪测量卫星到地面目标的精确距离;星敏感器测定卫星姿态角度;双频GPS天线测定卫星在WGS84参考系的坐标。激光足印坐标需经过三维坐标解算将激光测距仪采集的距离值结合卫星位置及姿态角度转换为WGS84参考系下的三维坐标[15]。激光足印定位几何模型如下
| $ \left[ {\begin{array}{*{20}{c}} {{X_{{\rm{CTS}}}}}\\ {{Y_{{\rm{CTS}}}}}\\ {{Z_{{\rm{CTS}}}}} \end{array}} \right] = \mathit{\boldsymbol{R}}_{{\rm{CIS}}}^{{\rm{CT}}}\mathit{\boldsymbol{R}}_{\mathit{\boldsymbol{SE}}}^{{\rm{CIS}}}\mathit{\boldsymbol{R}}_{\rm{E}}^{{\rm{SE}}}\left[ {{\bf{R}}_{\rm{L}}^{\rm{E}}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ \rho \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {X_{\rm{L}}^{\rm{E}}}\\ {Y_{\rm{L}}^{\rm{E}}}\\ {Z_{\rm{L}}^{\rm{E}}} \end{array}} \right]} \right] + {\left[ {\begin{array}{*{20}{c}} {{X_{\rm{S}}}}\\ {{Y_{\rm{S}}}}\\ {{Z_{\rm{S}}}} \end{array}} \right]_{{\rm{CTS}}}}. $ | (1) |
式中:[XCTSYCTSZCTS]T为激光足印在WGS84参考系下的坐标;RCISCTS为空间固定惯性参考系到地球固定地面参考系的旋转矩阵;RSECIS为轨道坐标系到空间固定惯性参考系的旋转矩阵;RESE为本体坐标系到轨道坐标系的旋转矩阵:RESE=
根据星载激光测高仪的工作原理可知,测高仪工作过程中主要存在指向、测距、姿态、轨道等误差。其中轨道误差是随机误差,可通过精密定轨方法加以削减;姿态、指向、测距偏差中包含大部分系统误差,姿态及指向误差对平面精度直接影响较大;而测距误差将直接影响高程精度,测距误差因素中的潮汐和大气延迟可以通过潮汐和大气延迟改正模型加以消除[3]。
本文经误差分析,姿态及指向角误差具有等价的影响效果,在建模中作为同一项误差予以考虑以减少参数项,并由定位几何模型推导出几何定标模型如下
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{X_{{\rm{CTS}}}}}\\ {{Y_{{\rm{CTS}}}}}\\ {{Z_{{\rm{CTS}}}}} \end{array}} \right] = R_{{\rm{CIS}}}^{{\rm{CTS}}}R_{{\rm{SE}}}^{{\rm{CIS}}}R(\omega )R(\varphi )R(\kappa )\\ \left[ {R_{\rm{L}}^{\rm{E}}\left[ \begin{array}{l} 0\\ 0\\ {k_1}\rho + {k_2} \end{array} \right] + \left[ {\begin{array}{*{20}{c}} {X_{\rm{L}}^{\rm{E}}}\\ {Z_{\rm{L}}^{\rm{E}}} \end{array}} \right]} \right] + {\left[ {\begin{array}{*{20}{c}} {{X_{\rm{s}}}}\\ {{Y_{\rm{s}}}}\\ {{Z_{\rm{s}}}} \end{array}} \right]_{{\rm{CTS}}}}. \end{array} $ | (2) |
式中:激光测高仪定标参数为姿态角校正参数(ω, φ, κ)和激光测距修正参数(k1, k2)。k1为测距乘常数,k2为测距加常数。以上述5个误差改正数为未知数,用泰勒公式对激光几何定标模型进行线性展开,得到误差方程如下
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {{X_{{\rm{CTS}}}}}\\ {{Y_{{\rm{CTS}}}}}\\ {{Z_{{\rm{CTS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_0}}\\ {{Y_0}}\\ {{Z_0}} \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {X_{{\rm{CTS}}}}}}{{\partial \omega }}}&{\frac{{\partial {X_{{\rm{CTS}}}}}}{{\partial \varphi }}}&{\frac{{\partial {X_{{\rm{CTS}}}}}}{{\partial \kappa }}}&{\frac{{\partial {X_{{\rm{CTS}}}}}}{{\partial {k_1}}}}&{\frac{{\partial {X_{{\rm{CTS}}}}}}{{\partial {k_2}}}}\\ {\frac{{\partial {Y_{{\rm{CTS}}}}}}{{\partial \omega }}}&{\frac{{\partial {Y_{{\rm{CTS}}}}}}{{\partial \varphi }}}&{\frac{{\partial {Y_{{\rm{CTS}}}}}}{{\partial \kappa }}}&{\frac{{\partial {Y_{{\rm{CTS}}}}}}{{\partial {k_1}}}}&{\frac{{\partial {Y_{{\rm{CTS}}}}}}{{\partial {k_2}}}}\\ {\frac{{\partial {Z_{{\rm{CTS}}}}}}{{\partial \omega }}}&{\frac{{\partial {Z_{{\rm{CTS}}}}}}{{\partial \varphi }}}&{\frac{{\partial {Z_{CTS}}}}{{\partial \kappa }}}&{\frac{{\partial {Z_{{\rm{CTS}}}}}}{{\partial {k_1}}}}&{\frac{{\partial {Z_{{\rm{CTS}}}}}}{{\partial {k_2}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \omega }\\ {\Delta \varphi }\\ {\Delta \kappa }\\ {\Delta {k_1}}\\ {\Delta {k_2}} \end{array}} \right]. \end{array} $ | (3) |
在定标计算中,利用最小二乘原理解算误差改正数。
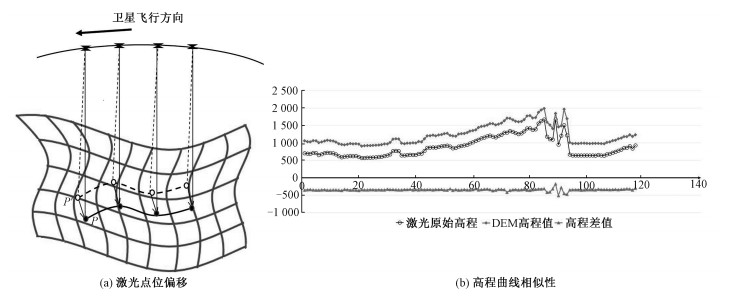
1.2 基于曲线匹配的测高仪无场几何定标方法 1.2.1 基于曲线匹配的控制点获取在理想状况下,星载激光测高仪垂直向下指向地表。由于卫星发射时的振动以及入轨后空间环境的变化等因素影响,激光测高仪的指向、测距等系统参数相对于发射前地面测量值发生变化,在轨的姿态角度测量存在偏差,从而引起激光足印的平面和高程误差[4]。因为国产高分辨率遥感卫星一般采用大平台、三轴姿态稳定系统[3],测高仪在轨运行期间系统指向比较稳定,整轨激光点的姿态误差变化极小,使得激光足印的实际轨迹应与系统在无误差时的轨迹保持近似平行,高程曲线形态趋于一致具有相似性。如图 1(a)所示,P′为在未定标前计算所得的激光足印序列位置,P为激光足印序列实际的位置;图 1(b)为原始激光高程曲线与地面DEM高程曲线相似性示意图。
|
Download:
|
| 图 1 激光点位偏移及高程曲线相似性示意图 Fig. 1 Schematic diagrams of laser point offset(a) and elevation curve similarity(b | |
基于上述原理,可以用初始的激光足印序列平面坐标为基础在参考DEM数据上进行搜索匹配,获得激光足印的实际位置作为定标计算的控制点。具体的方法如下:
1) 激光点初始坐标计算,获得点集S(B0L0H0), 由S(H0)组成初始高程曲线图curve-0;
2) 将激光初始平面坐标S(B0L0)沿DEM格网按一定的步进平移,内插获取S(H)集合,并组成n条DEM高程曲线图:curve-1, ……, curve-n;
3) 将原始高程曲线curve-0与n条DEM点高程曲线进行匹配,最佳匹配DEM点集作为初始激光足印的控制点参与定标参数的计算。在遍历区域范围内,激光初始高程点集与DEM对应点高程差值的方差最小所对应的DEM数据的地理坐标定为激光足印的控制点坐标,即:
| $ {\rm{GCP}} = \min \left\{ {{\mathop{\rm var}} \left( {S\left( {\Delta {H_{ji}}} \right)} \right)} \right\}, $ | (4) |
| $ \Delta {H_{ji}} = {x_i} - {y_{ji}}(j \in (1, n)). $ | (5) |
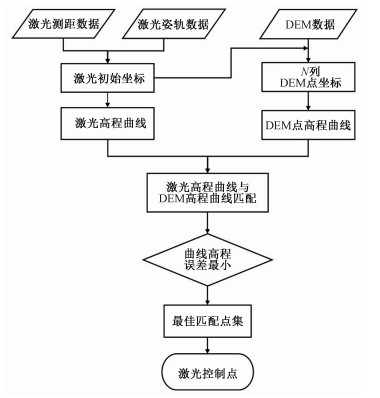
式中:xi为激光序列第i个点的高程值,yji为第j条DEM高程曲线的第i个点的高程值。计算流程如图 2所示。
|
Download:
|
| 图 2 激光足印控制点获取流程 Fig. 2 Control point acquisition procedure of laser footprint | |
激光原始测距数据中包含有大气延迟及潮汐误差等误差项,因此需要进行数据预处理,即构建精确的大气延迟校正模型[16]和潮汐误差校正模型[17],修正原始激光测距值。利用校正后的激光测距数据及对应时刻的卫星姿轨数据、地面控制点坐标代入定标模型,根据最小二乘原理即可求解出系统几何定标参数。再将定标后获得的系统姿态角、测距参数代入式(1)依次对整轨激光点进行计算,并以DEM对应平面坐标上的高程为参考真值来评价激光几何定标后激光足印高程的精度。若整轨有n个激光点,统计高程残差(单位:m)的均值及中误差为:
| $ \Delta \bar H = \frac{{\sum\nolimits_{i = 1}^{i = n} {} \left( {{H_i} - H_i^\prime } \right)}}{n}, $ | (6) |
| $ \sigma H = \sqrt {\frac{{\sum\nolimits_{i = 1}^{i = n} {} {{\left( {{H_i} - H_i^\prime } \right)}^2}}}{n}} . $ | (7) |
将以上高程残差的均值
本文实验采用由中国资源卫星应用中心提供的资源三号02星0级激光测高数据。每组测高数据由激光测距文件、卫星轨道文件、卫星姿态文件3个文件组成,分别提供激光器到目标的距离信息,卫星在WGS84坐标系中的坐标速度信息以及卫星平台的姿态四元数。实验中考虑到激光足印所在区域的地形影响,平坦的区域可以保证激光测高数据的精度,高差变化较大的区域虽测高精度稍差但可以使得高程曲线体现地形特征,两者的结合有利于曲线匹配时获取更为准确的激光足印控制点坐标。本文实验中选取轨道编号为675轨中的117个激光足印数据(数据采集时间为2016年8月9日)进行控制点获取实验及定标参数计算。这117个激光足印中有约2/3位于平坦的内蒙古草原及戈壁区域,1/3位于高低起伏较大的山区。实验另选取602、630、632轨等共计10轨激光数据来进行定标前后测高精度的评估分析。用于无场激光控制点匹配获取及测高精度评定的地表高程数据为ASTER GDEM(V2版),来源于中国科学院计算机网络信息中心地理空间数据云平台。
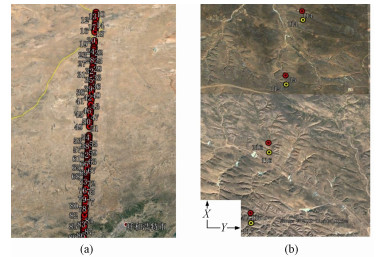
2.2 控制点获取与定标参数计算按照基于曲线匹配的控制点获取的算法流程,采用表 1的定标参数初值,将初步去除大气及潮汐影响的激光测高数据集合组成的高程曲线在DEM的一定范围内搜索最为匹配的高程曲线。激光初始坐标的平移搜索采用先整体后局部的思想,步进分别为100,10,1m。实验中用于控制点获取的675轨中的117个激光足印初始坐标所在的平面投影位置如图 3(a)所示,主要分布在内蒙古自治区境内。图 3(b)中,红色点为激光足印原始平面投影坐标,黄色的点是最佳匹配获得的对应激光足印的控制点坐标,坐标平面上偏移的量分别为X向下偏移481m,Y向右平移43m。根据激光足印初始坐标与相应控制点坐标的差异计算所得定标参数,如表 1所示。
|
|
表 1 姿态角及激光测距定标参数 Table 1 Attitude angle and laser ranging calibration parameters |
|
Download:
|
| 图 3 初始激光足印及部分激光足印控制点分布图 Fig. 3 Control point distribution maps of initial laser footprint and partial laser footprint | |
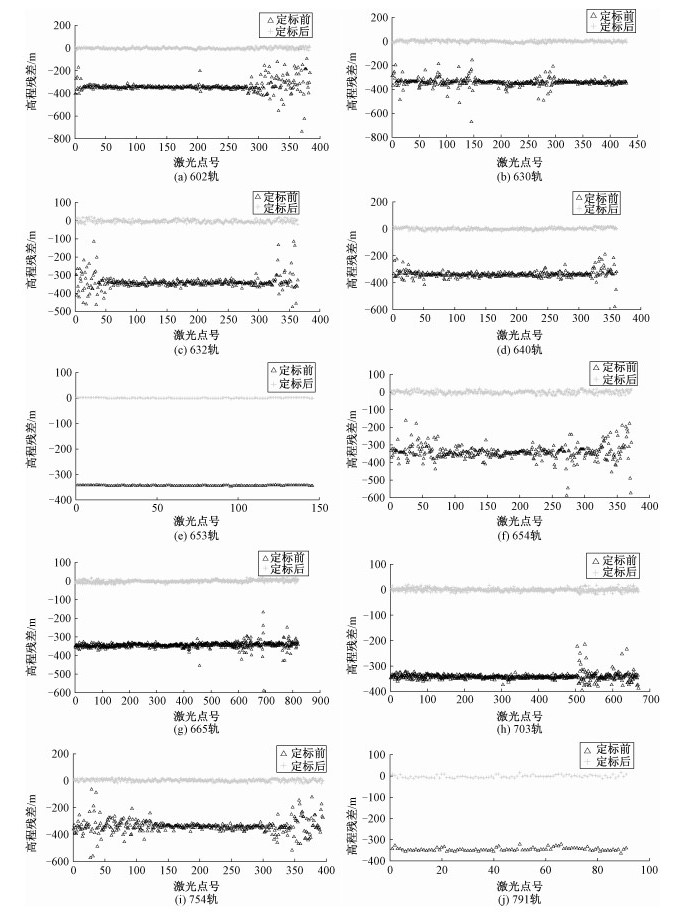
本文对23轨资源三号02星激光测高数据进行定标处理,选取其中的10轨激光数据作为代表进行分析。通过对比定标前后高程残差的均值及中误差验证本文中无场定标方法的效果。表 2为各轨激光测高数据定标前后高程残差均值、中误差统计表。图 4分别是602、630、632、640、653、654、665、703、754、791轨剔除粗差值之后的激光点定标前后高程残差对比图,其中黑色三角点代表定标前激光高程残差,浅灰色十字点代表定标后激光高程残差。
|
|
表 2 激光测高数据定标前后高程残差均值及中误差统计表 Table 2 Average and residual error statistics of elevation residual before and after laser altimetry data calibration |
|
Download:
|
| 图 4 各轨激光点定标前后高程残差对比 Fig. 4 Comparison of elevation residuals before and after laser point calibration for each track | |
从表 2及图 4可以看出,这10轨激光数据的定标前的高程残差均值在-336~-346之间,中误差在338~346m之间,高程残差值较大,数据分布较为分散,主要是因为所使用的实验数据为0级激光数据,未经过实验室定标参数的校正,系统误差还未消除。经过无场定标参数校正后,激光测高数据的高程残差均值下降到3.2m以内,中误差下降到10m以内,高程残差明显减小,每轨激光数据的高程精度提升97.2%以上。由此可见,系统误差基本消除。其中602、630、632、640、654、754轨中约有一半激光足印分布在高差变化较大的山区,激光测高精度受到地形的较大影响,所以其校正后中误差仍偏大。而665、703轨位于西亚高原地区,地表多为荒漠及稀疏草原,激光测高数据质量较好,经校正后残差均值接近为零,中误差也较小。791轨的91个激光足印位于中国华北平原地区,地势平坦,但是地表覆盖类型丰富,会影响地面高程测量精度,所以其中误差虽较小,但残差均值仍有1.78m。最后,653轨的146个激光足印位于黄海及东海区域,高程残差均值定标后为0.38m,中误差小于1.1m,高程精度提升99.6%,定标后数据精度提升效果非常明显。
3 总结激光测高仪在轨几何定标是获得高精度测高数据的关键环节。本文在充分研究现有定标方法的基础上探索一种无需布设野外定标场地的测高仪在轨几何定标方法。该方法利用激光足印高程曲线与DEM进行最优化匹配获得激光足印控制点进而实现定标参数求解。实验表明,资源三号02星0级激光测高数据经过本文的无场定标方法校正后,其高程残差均值下降到3.2m以内,中误差下降到10m以内,数据精度提升97.2%以上,证明了本方法的有效性,可作为地面探测器定标法的有效补充。后续考虑采用更高精度的DEM数据来提高无场定标的效果。
作者致谢国家民用空间基础设施“十二五”陆地观测卫星地面系统项目——高精度激光测高数据处理软件。| [1] |
李然, 王成, 苏国中, 等. 星载激光雷达的发展与应用[J]. 科技导报, 2007, 25(14): 58-63. Doi:10.3321/j.issn:1000-7857.2007.14.010 |
| [2] |
崔成玲, 李国元, 黄朝围.国内外星载激光测高系统发展现状与趋势[C].中国测绘地理信息年会, 2015-10: 288-295.
|
| [3] |
韩玲, 田世强, 谢俊峰. 星载激光测高仪检校技术发展现状浅析[J]. 航天返回与遥感, 2016, 37(6): 11-19. Doi:10.3969/j.issn.1009-8518.2016.06.002 |
| [4] |
唐新明, 谢俊峰, 付兴科, 等. 资源三号02星激光测高仪在轨几何检校与试验验证[J]. 测绘学报, 2017, 46(6): 714-723. |
| [5] |
岳春宇, 何红艳, 鲍云飞, 等. 星载激光高度计几何定位误差传播分析[J]. 航天返回与遥感, 2014, 35(2): 81-86. Doi:10.3969/j.issn.1009-8518.2014.02.012 |
| [6] |
易洪, 李松, 翁寅侃, 等. 自然地表测距残差对激光测高系统的在轨检校[J]. 华中科技大学学报(自然科学版), 2016, 44(8): 58-61. |
| [7] |
Sirota J M, Bae S, Millar P, et al. The transmitter pointing determination in the geoscience laser altimeter system[J]. Geophysical Research Letters, 2005, 32(L22S11): 1-4. |
| [8] |
Schutz B E, Zwally H J, Shuman C A, et al. Overview of the ICESat mission[J]. Geophysical Research Letters, 2005, 32(L21S01): 1-4. |
| [9] |
Martin C F, Thomas R H, Krabill W B, et al. ICESat range and mounting bias estimation over precisely-surveyed terrain[J]. Geophysical Research Letters, 2005, 32(L21S07): 1-4. |
| [10] |
Magruder L A, Webb C E, Urban T J, et al. ICESat altimetry data product verification at White Sands Space Harbor[J]. Ieee Transactions on Geoscience And Remote Sensing, 2007, 45(1): 147-155. Doi:10.1109/TGRS.2006.885070 |
| [11] |
Magruder L A, Ricklefs R L, Silverberg E C, et al. ICESat geolocation validation using airborne photography[J]. Ieee Transactions on Geoscience And Remote Sensing, 2010, 48(6): 2758-2766. Doi:10.1109/TGRS.2010.2040831 |
| [12] |
李国元, 唐新明. 资源三号02星激光测高精度分析与验证[J]. 测绘学报, 2017, 46(12): 1939-1949. Doi:10.11947/j.AGCS.2017.20170174 |
| [13] |
张过, 李少宁, 黄文超, 等. 资源三号02星对地激光测高系统几何检校及验证[J]. 武汉大学学报(信息科学版), 2017, 42(11): 1589-1596. |
| [14] |
唐新明, 谢俊峰, 莫凡, 等. 资源三号02星激光测高仪足印位置预报方法[J]. 测绘学报, 2017, 46(7): 866-873. |
| [15] |
唐新明, 李国元, 高小明, 等. 卫星激光测高严密几何模型构建及精度初步验证[J]. 测绘学报, 2016, 45(10): 1182-1191. Doi:10.11947/j.AGCS.2016.20150357 |
| [16] |
Herring T A, Quinn K J. The algorithm theoretical basis document for the atmospheric delay correction to GLAS laser altimeter ranges[R]. NASA/TM-2012-208641.Vol 8. NASA, 2012.
|
| [17] |
Fricker H A, Ridgway J R, Minster J B, et al. The algorithm theoretical basis document for tidal corrections[R]. NASA/TM-2012-208641.Vol 9. NASA, 2012.
|
 2020, Vol. 37
2020, Vol. 37 


