受控聚变反应堆是未来最终解决人类能源问题,实现永久清洁能源的重要途经之一。聚变反应堆存在多种形式,如使用磁约束的托克马克装置(Tokamak)。在聚变堆中面向等离子体的第一壁上会积聚反应堆所产生的大量热负荷,为带走第一壁上的热量,防止第一壁结构的损坏,同时避免等离子体对结构架的侵蚀,需要在第一壁上铺展液态金属用作防护层,高温的第一壁与冷却的液态金属之间存在温差,导致液态金属膜在壁面上产生自由对流。
自由对流是由于温差或浓度差(组分)导致流体密度变化,在流体内部产生体积力从而驱动流体,该体积力包括浮升力、重力、电磁场力等。对于内部自然对流,Wakashima和Saitoh[1]进行相关的实验、模拟和理论基准解研究。针对液态金属内部自然对流,法国国家科研中心[2-3]对水平磁场下长竖直方腔内的自然对流进行实验和模拟研究,研究结果表明,液态金属在磁场中的方腔内自然对流与换热机理不同于水和空气等一般介质,且不同的磁场方向与磁场强度对液态金属的流动换热影响也不同。在中强磁场条件下,增加磁场强度会明显地抑制液态金属的自然对流;而在弱磁场强度条件下,磁场对液态金属的流动表现出强化作用,且磁场对内部自然流动换热影响的转折点大约为0.3 T。
由于液态金属的不透明和导电性,对液态金属的速度测量变得尤为困难。超声波多普勒测速仪(UDV)可以通过声波反射技术获得液态金属内部的速度。研究表明,UDV采用声学反射接收技术测量不透明液体的流速,比PIV或者LDV等方法更具优势[4-5],该测量技术通过接收回波信号进行多普勒分析,获得不同深度上反射粒子的反射速度,且不会影响流体本身的内部流动,具有对不透明系统进行瞬时测量等优点。本文作者已开展液态金属在横向磁场条件下方腔内的自然对流与换热实验,获得了磁场对液态金属内部自然对流的换热规律[6-7]。不同于腔体内部的自然对流,竖直平板外部的自由对流没有外部壁面对流体流动的限制,研究过程中需要重点观察平板表面处流动与热边界层的分布与变化情况。对于外部自由对流,已有研究人员用实验方法研究分析等温竖直平板外部自由对流,获得竖直平板外部的自由对流问题数值解,给出普朗特数从0.01~1 000的介质下竖直平板自由对流的数值解[8],从经验关系式角度,已有研究人员通过数值计算获得竖直平板表面温度变化和恒热流条件时相应的相似解和关联式[9],开展竖直平板的自由对流强化换热实验研究[10]。从现有文献研究现状可以看出,对于外部自由对流研究,其研究对象以水或者空气等为换热介质,对液态金属在竖直平板上的外部自由对流和磁场作用等影响因素未见报道。同时液态金属在磁场条件下会产生不同于一般介质的磁流体力学(MHD)效应,以核聚变堆中液态金属在大温差情况下产生外部自由流动为实验背景,对液态金属在磁场下的竖直平板外的自由对流流动和换热规律的研究尤为必要。为进一步研究磁场对液态金属外部自由对流影响规律,本文设计不同磁场条件下液态金属在竖直平板表面的自由对流实验系统,以液态金属镓铟锡合金为实验介质,开展磁场影响下电加热情况下的竖直平板表面液态金属的自由对流与换热规律研究。
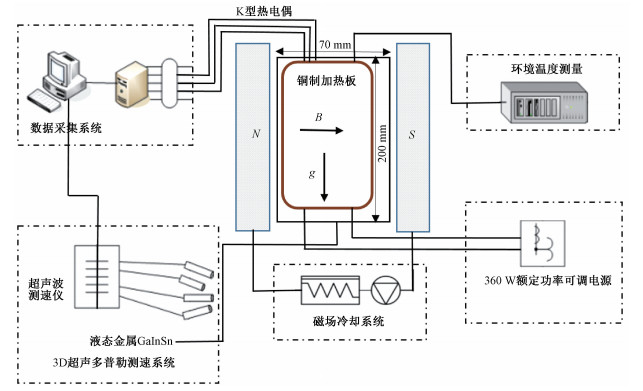
1 实验装置与介质图 1所示为液态金属在磁场中自由流动的实验装置示意图。实验腔体的宽度设置为70 mm,高度设置为200 mm,长度设置为200 mm,材质为有机玻璃的长方体开口盒子。平板加热器为宽度50 mm,高度120 mm的铜制加热板,为均匀热量同时测量表面热流密度,在加热片表面采用同尺寸且厚度为20 mm的铜板。在距离铜板两侧2 mm处开半径为1.5 mm且深为15 mm的孔用以布置热电偶,位于铜板的左右上下对称共20处。在连接热电偶时,为获取良好的测量数据,保证热电偶与铜板充分地接触,采用铜粉在热电偶探头与铜板之间压实,达到热电偶与铜孔的完美接触,在孔口使用密封胶将铜板与热电偶连接线粘合固定。同时为了减小加热板对外的热量耗散,在铜板四周除加热面外,都使用厚度为5 mm的聚四氟乙烯板进行保温处理。
|
Download:
|
| 图 1 液态金属自由对流实验装置示意图 Fig. 1 Schematic diagram of experimental apparatus for free convection of liquid metal | |
实验测量竖直平板壁面的自由流动,考虑到实验测量的对称性以及液态金属的高密度和昂贵的价格,设置实验为单侧测量,即将加热平板放置于腔体的一侧,由于板面厚度且加热始端距腔体地面有足够距离,可以忽略不对称实验带来的误差。如图 2所示,加热板的温度测量使用K型热电偶,将热电偶与高速数据采集器连接,使测量数据经PC端显现,构成温度与数据采集系统1。环境温度的测量使用K型热电偶与双通道数字温度表相连接。

|
Download:
|
| 图 2 液态金属自由对流实验 Fig. 2 Liquid metal free convection experiment | |
对边界层速度的测量使用超声波多普勒测速仪(UDV)横向测量,如图 2中3部分所示,测量与实验腔体部分为图 2中5部分。使用360 W额定功率可调电源对加热板进行加热,加热系统为图 2中2部分,控制加热功率的范围在5~12 W。均匀磁场可容纳最大宽度为80 mm,磁场方向为水平向右且与重力方向垂直,磁场实验装置与冷却系统为图 2中4部分。
实验介质选择液态金属镓铟锡(Ga68%In20%Sn12%)合金,由于镓铟锡合金的高热导率以及高电导率,同时在常温条件下为液态,无毒易于操作,是研究MHD效应的理想实验工质,其物性参数如表 1所示。
|
|
表 1 液态金属(Galinstan合金)物性参数 Table 1 Physical properties of liquid metal (Galinstan) |
本文根据傅里叶导热定律可获得加热板表面的热流密度,同时假设铜板内温度线性分布,可以根据外侧热电偶所测温度线性推算获取加热板壁面温度。
根据牛顿冷却定律且认为铜板热量完全被液态金属自由对流带走,根据铜板表面温度和环境温差可以求得铜板表面的局部传热系数hx。实验变量包括施加电源功率,功率大小分别为3.6、4.6、5.6、6.7、7.9 W共5组;施加的磁场大小为0~1.5 T。
2 自由对流控制方程在关于强磁场作用下的平板外液态金属的自由对流换热研究中,Ivan和Michel[11]利用数值模拟的方法对液态金属锂铅合金的方腔内部自然对流进行研究。研究结果表明电磁力对液态金属流动和传热产生非单调变化的影响,因此在本文的研究过程中需要不断变化磁场强度观察其变化规律。
磁场力可视为施加在整个流体域的体积力,根据Helmholtz自由能可得。Landau等[12]对磁场力进行推导得到磁场力的表达式为
| $ F=\frac{1}{2} \nabla\left[B^{2} \rho\left(\frac{\partial \mu}{\partial \rho}\right)_{T}\right]-\frac{1}{2} B^{2} \nabla \mu+\varepsilon(J \times B). $ | (1) |
式中:B为外磁场强度,ε为流体磁导率,J为电流密度,ρ为流体密度。右边的第1项代表不均匀磁场导致的梯度磁场力,第2项为温差导致的不均匀磁导率产生的磁场力。本文研究均匀磁场作用下导电流体的自然对流,且液态金属合金为弱磁性物质,忽略其磁导率带来的影响,该两项之和为零。第3项为Lorentz力。所以,在均匀磁场条件下对液态金属所产生的磁场力可简化为
| $ F=\varepsilon(J \times B). $ | (2) |
包含磁场力的不可压缩流体液态金属稳态的外部自然对流控制方程组为:
| $ \nabla \cdot \boldsymbol{U}=0, $ | (3) |
| $ \rho(\boldsymbol{U} \cdot \nabla) \boldsymbol{U}=-\nabla P+\rho v \nabla^{2} \boldsymbol{U}-\rho \boldsymbol{g}+\boldsymbol{F}, $ | (4) |
| $ \rho C_{P}(\boldsymbol{U} \cdot \nabla) T=k \nabla^{2} T. $ | (5) |
式中:U为速度矢量,P为压力,v为流体的运动黏度,T为流体温度,β为容积膨胀系数,g为重力加速度,F为洛伦兹力,CP为定压比热容,k为流体的热导率。
从控制方程中可以看出电磁力对液态金属自由对流动量输运会产生很大的影响,进一步影响其能量输运过程,对其进行实验研究能准确快速获得磁场对自由对流换热的影响规律。
为表征液态金属在磁场中的流动与传热特性以及磁场对流体流动换热的影响,需要引入无量纲准则数进行分析。Nu数为对流传热中表征流体换热大小的无量纲参数,其计算关系式如下
| $ N u=\frac{h L}{k}, $ | (6) |
式中:h为表面局部换热系数,L为特征尺度,k为流体的热导率。
Gr数是表征流体自由对流浮升力与黏性力相对大小的无量纲参数,其计算关系式如下
| $ G r=\frac{g \beta L^{3} \Delta T}{v^{2}}, $ | (7) |
式中,ΔT为流体与环境温差。
在磁场条件下,为表征磁场对液态金属流动与传热产生的影响,引入Ha数作为衡量标准。其计算关系式如下
| $ H a=B L \sqrt{\sigma / \mu}, $ | (8) |
式中:B为磁场强度,σ与μ分别为液态金属的导电率和动力黏度。本文Ha数范围大约为0~450。
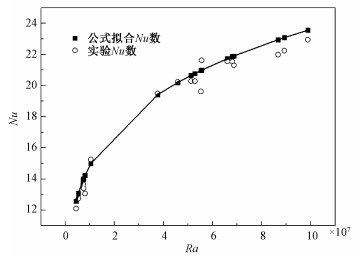
3 自由对流实验结果分析 3.1 实验结果准确性本文实验涉及传热和温度测量精度等误差,需要对实验结果进行误差分析。为检测实验模型准确性,对竖直平板在水中自由对流进行实验验证,并与已有结果相比较。利用竖直平板在水中的自由对流进行实验系统的准确性验证,得到平板表面随瑞利数变化的局部努赛尔数分布如图 3所示,与半无限大平板下恒热流平板的无量纲数关联式[8]对比,最大误差小于10%表明本文实验系统的准确性。
|
Download:
|
| 图 3 实验结果准确性验证图 Fig. 3 Accuracy verification of experimental results | |
在恒定的加热功率条件下(P=6.2 W),测量不同磁场强度下的液态金属在竖直平板上的流动边界层速度分布。采用多普勒超声波测速仪(UDV)的4 MHz超声波探头,与竖直平板呈60°多普勒夹角,设置液态金属声速为2 730 m/s,以液态金属氧化粒子作为超声波示踪粒子,观察测量所得速度与超声波回波位置,测量无磁场和不同磁场条件下流动边界层的速度分布。
研究表明当磁场强度小于0.05 T时,增加磁场强度会强化边界层流动速度,使换热增强;而当磁场强度大于0.05 T时,增强磁场会明显地抑制边界层的流动速度,换热被削弱。
参照文献[2-3]的研究对外部自由对流的流场进行分析可知,在无磁场条件下,液态金属的自由对流受浮升力的驱动,表现出复杂的、随时间振荡的三维流场。当施加小磁场时,液态金属的流场受到抑制,流动结构从三维流动转化为准二维流动,也因此降低了流场在三维方向的动量和能量输运,从而使主流方向流动和换热强化。但随着磁场强度的提高,外加磁场对流动的抑制作用逐渐占据主导。所以在小磁场强度下,流动从三维转向准二维时传热效率会有所提高。
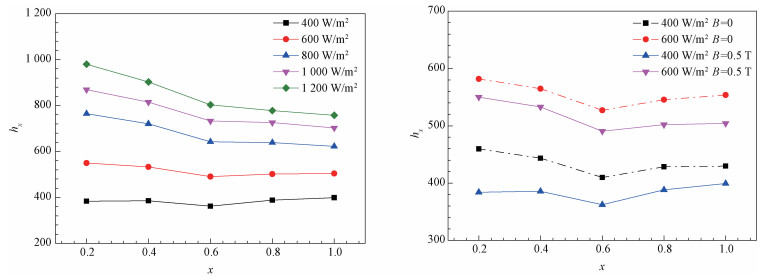
3.3 磁场影响下的换热分析实验过程中设定恒定的磁场强度并改变电源的加热功率,在不同的热流密度条件下,对比液态金属在0.5 T磁场强度时的局部换热系数与努塞尔数Nu随特征长度x的变化趋势。图 4给出无磁场和施加0.5 T磁场时不同热流密度的局部换热系数和有无磁场时局部换热系数的对比情况。
|
Download:
|
| 图 4 局部对流换热系数结果 Fig. 4 Local heat transfer coefficient under the influence of a magnetic field | |
从图 4可以看出,平板表面的局部传热趋势呈下降趋势,由于加热平板导致自由对流流体向上流动,不断加热壁面介质温度,在热流密度恒定的条件下,壁面与环境温差增大,从而降低了表面局部换热系数。同时随着功率的增加使得热流密度增加,所以表面局部热流密度会随着功率的增加而上升。在靠近平板尾部的位置局部传热系数上升,是因为腔体的限制在竖直平板尾部产生回流,回流对平板有再次冷却的作用,使得壁面与环境的温差减小,提高尾部的局部换热系数。虚线为无磁场条件下平板表面的局部传热系数,实线为0.5 T磁场条件下平板表面的局部传热系数。在恒定热流密度的条件下,磁场的存在会普遍降低平板的局部传热系数,由于磁场抑制自由对流效应,导致壁面温度升高,从而提高了壁面与环境的温差,所以磁场降低了平板表面的局部传热系数。
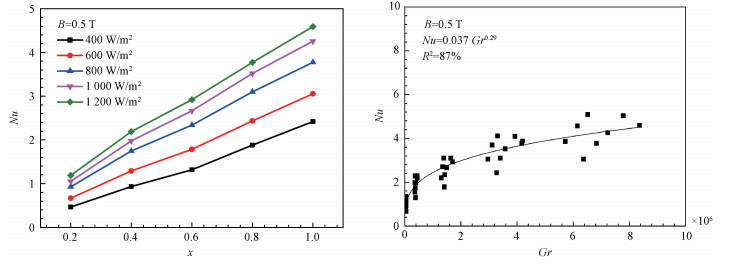
图 5给出不同热流密度条件下,液态金属在0.5 T磁场强度竖直平板表面的局部对流换热准则数Nu分布情况,对流换热与特征长度呈正相关,当特征长度增加时,对流换热加强。同时,提高加热功率导致表面热流密度的增加,增强了对流换热。
|
Download:
|
| 图 5 不同热流密度下竖直平板局部Nu数 Fig. 5 Local Nu number of vertical plate under different heat flux densities | |
根据0.5 T磁场强度下的实验结果,可以得到在磁场强度为0.5 T时,平板各点的对流换热努塞尔数Nu随格拉晓夫数Gr的变化趋势,并采用幂函数拟合得到Nu数与Gr数的曲线方程。曲线的拟合方程为
| $ N u=0.037 G r^{0.29}. $ | (9) |
为了进一步分析平板在恒定加热功率下,不同磁场强度下的液态金属自由对流换热规律,引入表征哈特曼数Ha与格拉晓夫数Gr的相对大小的磁相互作用数(N)如下
| $ N=H a^{2} / \sqrt{G r}. $ | (10) |
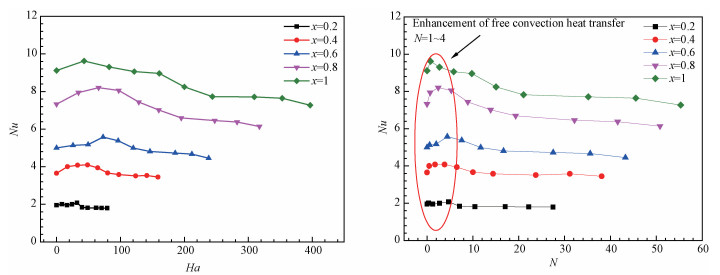
如图 6所示为恒定加热功率时,竖直平板壁面局部Nu数随哈特曼数的变化情况,平板壁面处的局部Nu数随着Ha数的变化先是增加,然后降低。
|
Download:
|
| 图 6 不同磁场下局部Nu随Ha和N变化 Fig. 6 Local Nu variation with Ha and N | |
在变化的磁场强度中,当Ha数小于50时,磁场会强化竖直平板表面的自由对流换热;而当Ha数高于75时,磁场会抑制自由对流换热。同时图 6中给出平板壁面局部Nu数随着磁相互作用数N的变化趋势。可以发现,随着特征长度x(即格拉晓夫数Gr)的增加,Nu数极值所对应的磁相互作用N变得越来越小。在x=0.2时,Nu数的极值分布在N=4左右,而当x=1时,Nu数的极值所对应的磁相互作用数大约等于1。根据实验结果发现该转折点出现在磁相互作用数为1~4的范围,这个规律和磁场对液态金属内部自然对流影响规律具有一致性,因此表明磁相互作用数N能更清晰地反映磁场对液态金属自然对流或自由对流换热的影响规律。
4 结论本文实验研究液态金属在磁场作用下恒热流加热竖直平板的自由对流作用,对不同热流密度和不同磁场强度下的工况进行实验研究,发现竖直平板表面的局部传热系数由下至上呈递减趋势,说明板面的换热由下至上逐渐降低。
在相同磁场强度下,随着加热功率的增加,竖直平板表面的局部传热系数普遍增大,换热增强,但随着功率的增加,表面传热系数与对流换热增幅会降低。
测量距加热始端30 mm处不同磁场强度下的流动边界层速度,得到在500 Gs磁场强度之前,液态金属边界层流动逐渐强化;在500 Gs磁场强度之后,边界层流动被抑制,该趋势与对流换热相同。在中强磁场时,靠近壁面处的流动被完全抑制为零。
在中强磁场条件下,磁场作用会抑制平板表面的自由流动。随着Ha数的增加,对流换热系数Nu数会普遍降低。在0.5 T磁场强度下,根据实验结果拟合得到平板Nu数随着Gr数的变化曲线和经验关系式。
在弱磁场中,竖直平板的自由流动会随着磁场的增加被强化。在对流换热Nu数与哈特曼数的关系中,Nu数的极值所对应的哈特曼数在50左右。在对流换热Nu数与磁相互作用数N的关系中,Nu数的极值所对应的磁相互作用数在1~4之间,并随着Gr数的增加极值逐渐减小。这个规律和磁场对液态金属内部自然对流影响规律具有一致性,表明磁相互作用数N能更清晰地反映磁场对液态金属自然对流或自由对流换热的影响规律。
| [1] |
Wakashima S, Saitoh T S. Benchmark solutions for natural convection in a cubic cavity using the high-order time-space method[J]. International Journal of Heat and Mass Transfer, 2004, 47(4): 853-864. Doi:10.1016/j.ijheatmasstransfer.2003.08.008 |
| [2] |
Tagawa T, Authié G, Moreau R. Buoyant flow in long vertical enclosures in the presence of a strong horizontal magnetic field. Part 1. Fully-established flow[J]. European Journal of Mechanics B Fluids, 2002, 21: 383-398.
|
| [3] |
Authié G, Tagawa T, Moreau R. Buoyant flow in long vertical enclosures in the presence of a strong horizontal magnetic field. Part 2. Finite enclosures[J]. European Journal of Mechanics B Fluids, 2003, 22: 203-220. Doi:10.1016/S0997-7546(03)00024-4 |
| [4] |
Wang Z H, Wang S D, Meng X, et al. UDV measurements of single bubble rising in a liquid metal Galinstan with a transverse magnetic field[J]. International Journal Multiphase Flow, 2017, 94: 201-208. Doi:10.1016/j.ijmultiphaseflow.2017.05.001 |
| [5] |
Zhang C, Eckert S, Gerbeth G. Experimental study of single bubble motion in a liquid metal column exposed to a DC magnetic field[J]. International Journal Multiphase Flow, 2005, 31: 824-842. Doi:10.1016/j.ijmultiphaseflow.2005.05.001 |
| [6] |
Wang Z H, Meng X, Ni M J. Liquid metal buoyancy driven convection heat transfer in a rectangular enclosure in the presence of a transverse magnetic field[J]. International Journal of Heat and Mass Transfer, 2017, 10(113): 514-523. |
| [7] |
王增辉, 陈欢, 杨嵩. 磁场作用下三维方腔内液态金属自然对流的数值模拟[J]. 中国科学院大学学报, 2013, 30(4): 472-477. |
| [8] |
Kays W, Crawford M, Weigand B, et al.对流传热与传质[M].赵镇南, 译.北京: 高等教育出版社, 2007.
|
| [9] |
Fujii T, Fujii M. The dependence of local Nusselt number on Prandtl number in the case of free convection along a vertical surface with uniform heat flux[J]. International Journal Heat Mass Transfer, 1976, 19: 121-122. Doi:10.1016/0017-9310(76)90020-X |
| [10] |
闻洁, 于兆吉, 吴宏. 竖直平板自由对流强化换热的实验[J]. 航空动力学报, 2008, 23(3): 410-414. |
| [11] |
Ivan D P, Michele C. MHD free convection in a liquid-metal filled cubic enclosure differential heating[J]. International Journal of Heat and Mass Transfer, 2002, 45(7): 1477-1492. Doi:10.1016/S0017-9310(01)00252-6 |
| [12] |
Landau L D, Lifshitz E M, King A L, et al. Electrodynamics of Continuous Media[J]. American Journal of Physics, 1961, 29(9): 647-648. |
 2020, Vol. 37
2020, Vol. 37 


