2. 中国科学院遥感与数字地球研究所, 北京 100094
2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China
SAR影像上地物的位置信息是地形测绘、灾害监测、资源普查、变化检测等空间对地观测技术应用的基础信息[1]。在摄影测量遥感领域,高精度的三维定位技术一直是研究的重点和难点[2]。机载重轨干涉合成孔径雷达(repeat pass interferometric synthetic aperture radar, RP-InSAR)[3-6],突破了双天线系统受载机平台尺寸的限制,实现不同时间重复观测相同区域,在局部地区的地形测绘和形变监测中具有不可替代的作用。机载重轨测量中,满足多波段测绘要求,基线长度可增至几百米。然而基线长度越大,获取图像像元高精度三维信息的难度越大。
机载重轨InSAR要求载机飞行轨迹高度重合,保持在与预设理想航迹相差±5 m的范围内,天线波束指向在±20°内变化,精度维持在1°以内[7]。干涉图像对的高相干性保证DEM的高精度。重轨InSAR的飞行轨迹必须保持在空间基线附近的一个很小的圆柱范围内。不同于机载双天线InSAR的刚性基线结构,在现有的GPS系统和惯性导航系统条件下,机载重轨InSAR测量两次的飞行轨迹,难以保证重合性。
机载重轨InSAR通常基线较长,飞机飞行航迹严重偏离理想航迹,机载重轨InSAR图像几何畸变明显,干涉图像对之间相对形变明显,同名像元对应不同地面大小,造成干涉处理困难。基线越长,干涉图像对之间的相对形变越明显,尤其在远斜距端,失配越发严重,干涉图像对的相干性越低,无法获取高精度DEM,亦无法实现高精度三维定位。
多项式模型法[8-9]、共线方程法[10]和距离多普勒模型法(range-Doppler model,RD)[11]是主要的传统机载SAR图像定位方法。
严格意义上,多项式模型和共线方程模型,不能实现图像的自动实时定位,不存在明确的物理意义,并不符合SAR侧视成像原理。多项式模型和共线方程模型在反演模型参数,实现定位校正时,严重依赖控制点信息[12]。
距离多普勒模型符合SAR侧视成像原理,具有明确的几何关系和物理意义[13],因而目前在SAR影像定位中使用较多。
岳昔娟等[14]基于差分GPS和惯性导航系统数据,在无控制点的情况下,根据RD模型和DEM数据,导出一种进行机载SAR影像主动定位的数学模型。
并试验验证此数学模型的正确性, 分析主要系统误差源及系统误差的改正方法。吴颖丹[15]针对星载合成孔径雷达对地目标的定位问题, 根据距离-多普勒模型和地球模型进行对地定位的理论和不同计算方法,系统地分析RD模型现有的解算方法。刘佳音等[16]提出一种新的SAR图像斜距多普勒定位模型的直接解法,推导出斜距多普勒定位模型的明确数学解析解,并与常用的数值迭代求解方法进行比较分析,仿真结果验证了推导的正确性。
张红敏等[17]针对无地面控制情况下的单幅SAR图像定位问题, 设计一种基于DEM和图像仿真的单幅SAR图像无控制定位方案。在外部DEM数据的支持下,将实际SAR图像与仿真SAR图像进行匹配来提取控制点以完成定向参数解算。张红敏等[18]还针对稀少控制下斜侧视SAR图像高精度定位难题,设计利用单个地面控制点的SAR图像立体定位方案。邱春平等[19]使用斜距与航向之间的夹角表示RD模型中的多普勒方程,推导SAR距离-斜视角模型的线性化形式, 设计相应的定向参数解算和立体定位方案。
为了解决机载重轨InSAR三维定位问题,本文提出一种机载重轨InSAR高精度三维定位方法。研究和推导机载重轨InSAR定位模型,利用POS数据和少量地面控制点信息,从精准SAR成像几何关系出发,实现干涉图像对精准的相对定位,生成高精度DEM;并利用高精度DEM,绝对定位图像像元,最终实现三维定位。
1 机载重轨InSAR形变分析机载单景SAR图像定位存在的主要问题是,载机飞行高度和姿态不稳定产生的图像畸变和雷达图像近距压缩的几何特点。一般来说,为了保证机载SAR图像同时实现方位向和距离向的高分辨率,载机飞行过程中应尽可能保持匀速直线运动。而实际情况是,受气流、GPS系统和惯性导航系统测量精度等的影响,载机在作非匀速飞行的同时会产生上下左右的偏转和抖动,极大地降低了成像质量和定位精度。非匀速运动的航迹会造成方位向采样不均匀;非直线运动的航迹会造成天线波束中心偏离,产生不规则几何畸变。
机载重轨InSAR三维定位,不仅需要解决单幅SAR图像的定位问题,还要解决干涉图像对之间相对定位不准确的问题。受POS系统实时精度的影响,重轨飞行航迹不完全重合且存在较大差异。造成自共同测绘带内测绘获得的干涉复图像对,距离向像元数不等。在长基线条件下,从SAR图像近距端到远距端,图像对失配情况俞加明显,难以保持相干性。
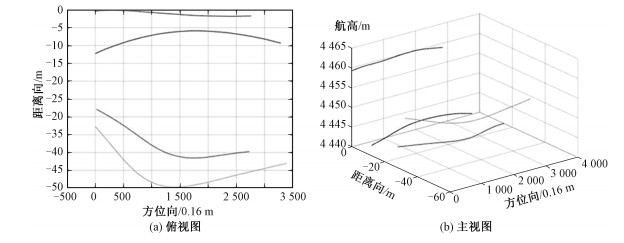
图 1显示选自2014年10月在海南陵水地区进行的重轨测绘中的4条载机飞行航迹,4条航迹均严重偏离预设航迹,差异明显。图中,航高和距离向坐标间隔1 m;方位坐标间隔0.16 m。
|
Download:
|
| 图 1 4条重轨航迹示意图 Fig. 1 Drawing of four repeat paths | |
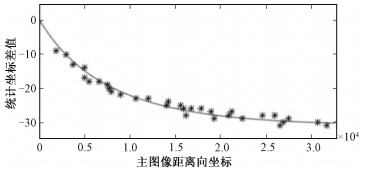
图 2中的散点表示统计得到的,一对重轨干涉SAR图像对上同名像元的距离坐标差值及其随斜距的变化趋势。随着斜距的增长,同名像元主辅图像的距离坐标差异逐渐增大,在近斜距端变化较快,在远斜距端变化渐缓。该现象说明在重轨机载InSAR中,存在干涉图像对随斜距增加,相干性逐渐降低的现象。
|
Download:
|
| 图 2 同名像元坐标差值及其变化趋势 Fig. 2 The coordinate differences and its trends of identical points | |
假设基线长度为B,基线倾角为α,r1为主天线斜距,r2为辅天线斜距,θ为斜视角。根据几何关系和余弦定理可得
| $ r_2^2 = r_1^2 + {B^2} + 2B{r_1}\cos \left( {\alpha + \theta } \right), $ | (1) |
即
| $ \theta = \arccos \left( {\frac{{r_2^2 - r_1^2 - {B^2}}}{{2B{r_1}}}} \right) - \alpha . $ | (2) |
式中:r22-r12≈(2r1+Δr)Δr,由相位差ϕ确定波程差Δr:
| $ \phi = \frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\Delta r \to \Delta r = \frac{{\lambda \phi }}{{2{\rm{ \mathsf{ π} }}Q}}. $ | (3) |
对于机载重轨干涉InSAR,Q=2。
因而,可以得出
| $ \theta = \arccos \left( {\frac{{\left( {2{r_1} + \Delta r} \right)\Delta r - {B^2}}}{{2B{r_1}}}} \right) - \alpha , $ | (4) |
P点的高度信息
| $ h = H - {r_1}\cos \theta , $ | (5) |
水平距离
| $ y = \sqrt {r_1^2 - {{\left( {H - h} \right)}^2}} . $ | (6) |
RD主动定位模型包括:距离方程、多普勒方程和椭球方程。
| $ \begin{array}{l} {\left( {{X_s} - X} \right)^2} + {\left( {{Y_s} - Y} \right)^2} + {\left( {{Z_s} - Z} \right)^2} = {R^2},\\ {V_x}\left( {{X_s} - X} \right) + {V_y}\left( {{Y_s} - Y} \right) + {V_z}\left( {{Z_s} - Z} \right) = - \frac{{{f_{{\rm{dol}}}}\lambda R}}{2},\\ \frac{{{X^2} + {Y^2}}}{{{{\left( {{R_{\rm{e}}} + h} \right)}^2}}} + \frac{{{Z^2}}}{{R_{\rm{p}}^2}} = 1. \end{array} $ | (7) |
式中:R=R0+m·j为目标点的斜距;R0为初始斜距;m为距离分辨率,j为目标点距离向坐标;(Xs, Ys, Zs)、(Vx, Vy, Vz)分别表示天线相位中心坐标和速度;fdol为多普勒频率偏移;λ为波长;(X, Y, Z)是目标点地面坐标;Re为地球椭球赤道半径;Rp=(1-f)·(Re+h),f为地球扁率;h为地面点高程。
3.2 定位参数改正将RD主动定位模型线性化,构建误差方程,代入地面控制点坐标(X, Y, Z),并根据最小二乘原理,求解dΧ:
| $ {\mathit{\boldsymbol{d}}_X} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right). $ | (8) |
式中,
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {F_1}}}{{\partial {R_0}}}}&{\frac{{\partial {F_1}}}{{\partial {Z_s}}}}\\ {\frac{{\partial {F_2}}}{{\partial {R_0}}}}&{\frac{{\partial {F_2}}}{{\partial {Z_s}}}}\\ {\frac{{\partial {F_3}}}{{\partial {R_0}}}}&{\frac{{\partial {F_3}}}{{\partial {Z_s}}}} \end{array}} \right],{\mathit{\boldsymbol{d}}_X} = \left[ {\begin{array}{*{20}{l}} {\Delta {R_0}}\\ {\Delta {Z_s}} \end{array}} \right],\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} { - F_1^0}\\ { - F_2^0}\\ { - F_3^0} \end{array}} \right]. $ | (9) |
设定阈值进行判断,比较
将改正值代入新的初始斜距和航高,假设存在地面点P,则点P的主图像地距为
| $ {P_{y1}} = \sqrt {{{\left( {{r_{{\rm{1new}}}} + {m_1}{j_1}} \right)}^2} - H_{{\rm{1new}}}^2} , $ | (10) |
式中:m1为图上斜距分辨率;j1是点P的图上斜距坐标;H1new=H1+Δh1,H1为主图像航高,Δh1为改正值;r1new=r1+Δr1,r1为主图像初始斜距,Δr1为改正值。
航迹2相对航迹1的地距偏移为ΔY。点P在辅图像上的斜距坐标j2new为
| $ {j_{2{\rm{new}}}} = \frac{{\sqrt {{{\left( {{P_{y1}} + \Delta Y} \right)}^2} + H_{2{\rm{new}}}^2} - {r_{2{\rm{new}}}}}}{{{m_2}}}. $ | (11) |
式中:H2new=H2+Δh2,H2为辅图像航高,Δh2为改正值;r2new=r2+Δr2,r2为辅图像初始斜距,Δr2为改正值。
根据j2new,重采样辅图像,获得像元一一对应的干涉图像对,完成机载重轨InSAR图像配准。
经过该处理之后,InSAR图像对之间的相对定位更加准确。
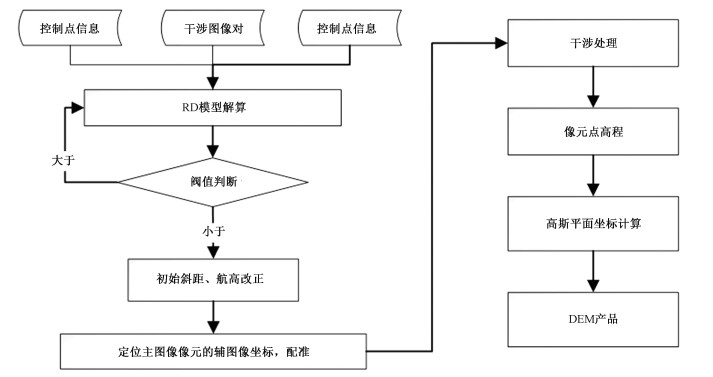
4 机载重轨InSAR图像定位机载重轨InSAR图像定位的流程如图 3所示,具体过程如下:
|
Download:
|
| 图 3 机载重轨InSAR图像定位的流程 Fig. 3 Flow chart of 3D location of airborne repeat pass InSAR | |
1) 获取模型参数,根据主图像像元坐标(i, j),读取其天线相位中心的瞬时位置向量(Xs, Ys, Zs)、速度向量(Vx, Vy, Vz)和斜距R。
2) 计算地心直角坐标系坐标原点,从地图头文件中读取SAR图像中心的大地经纬度(BC, LC),并转换坐标系
| $ \left[ {\begin{array}{*{20}{c}} {{X_0}}\\ {{Y_0}}\\ {{Z_0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\left( {N + {H_{{\rm{ave}}}}} \right)\cos {B_{\rm{C}}}\cos {L_{\rm{C}}}}\\ {\left( {N + {H_{{\rm{ave}}}}} \right)\cos {B_{\rm{C}}}\sin {L_{\rm{C}}}}\\ {\left( {N\left( {1 - {e^2}} \right) + H} \right)\cos {B_{\rm{C}}}} \end{array}} \right], $ | (12) |
式中:(X0, Y0, Z0)为地心直角坐标系初始值,Have是图像测绘区域的平均高程,N为地球曲率半径。
3) 主辅图像配准
RD模型解算并改正初始斜距和航高,计算主图像像元在辅图像上的距离向坐标,使用sinc插值法对辅图像进行重采样,获得像元大小一致且一一对应的干涉图像对。
4) 干涉处理
干涉处理分为相干计算、干涉滤波以及相位解缠绕等,最后获得解缠绕的相位图。
5) 高程计算
根据干涉几何关系,通过干涉相位计算主图像像元对应的地面高程。
6) 坐标转换
地心直角坐标系坐标(X, Y, Z)向高斯平面直角坐标系坐标(x, y)转换。
7) 计算像元灰度和高程
对应像元坐标(i, j)的灰度值σ(i, j)和高程值h(i, j)赋值给坐标转换后的像元。
5 试验与分析试验所用机载InSAR重轨图像为2014年10获取的,海南省陵水地区的测量结果。采用正侧式成像,分辨率0.5 m,所用波段为C波段,极化方式为VV极化,由POS AV 610系统获取POS数据。图像基本参数如表 1所示。选择距离向和方位向均匀分布的9个D级控制点,通过RD模型解算,改正初始斜距和航高后,计算图像像元在主辅图像的距离向坐标差值,即Δj=j2new-j1,如图 2中实线所示。
|
|
表 1 基本参数 Table 1 Basic parameters |
图 2中散点和实线在数值和变化趋势上的一致性说明,使用新到的初始斜距和航高,可以准确地定位主图像像元在辅图像上的位置,干涉图像对之间的相对定位更加精准。
为了确定本文方法对机载重轨InSAR图像的处理效果。选取几何畸变严重的远斜距区域进行相关处理,结果如图 4、图 5所示。
|
Download:
|
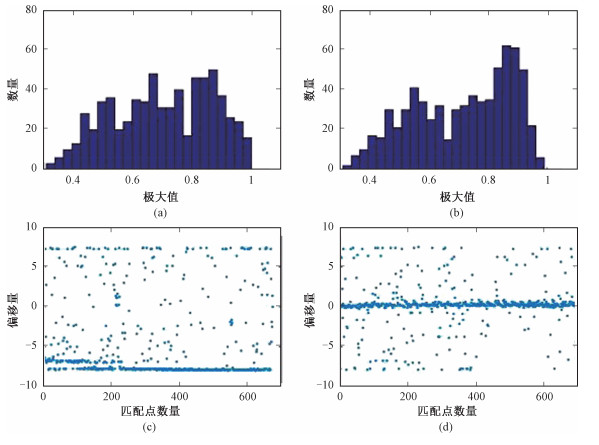
| 图 4 图像对相干性 Fig. 4 Coherence of image pairs | |

|
Download:
|
| 图 5 干涉处理结果 Fig. 5 Result of interfereometric processing | |
分别计算辅图像重采样之前和之后与主图像的相关性。设定相关窗口4×4;搜索窗口16×16,搜索窗口数目1 000,均匀分布在整个图像。评价参数是,全部搜索窗口内相关系数极大值的分布和窗口内部相关系数极大值点即匹配点的斜距坐标偏移量。
如图 4所示,图 4(a)、4(b)分别表示原图像对和新图像对的相关系数极大值分布直方图,4(c)、4(d)分别表示匹配的距离向坐标差值。图 4(b)的值分布明显高于图 4(a),峰值出现在0.9附近,说明新图像对的相干性整体更高;由图 4(c)显示匹配的绝大多数分布于窗口边缘,说明大部分干涉图像对的同名点分布于搜索窗口范围之外,而图 4(d)相对于图 4(c)变化更加明显,斜距坐标偏移量绝大多数分布于0值附近,说明干涉图像对的同名点基本分布于搜索窗口中心,新图像对的匹配性非常高,远超过原图像对。
图 5为试验数据的干涉处理结果。
试验区域地表信息保存完整,图像对相干性高,解缠绕相位图连续性好。高程变化敏感度高,在高度不同的地物类型分布区域,具有十分明显的高程变化。
上述试验结果表明,本文方法在实现InSAR复图像对精准相对定位的同时可以保持图像对之间的高度相干性,特别适合相对几何畸变随斜距增长而增大的长基线机载重轨InSAR图像对。使用检查点评价像元的三维定位,实测数据和计算数据比对如表 2所示。
|
|
表 2 定位精度分析 Table 2 Analysis of location accuracy |
对比检查点实测三维坐标和本文方法计算得到的三维坐标显示,方位向定位误差控制在0.32 m以内;距离向定位误差控制在0.8 m以内;高程误差控制在0.6 m之内,符合高精度三维定位的要求。
6 结论本文提出一种利用地面控制点,标定初始斜距和航高,获得高精度DEM数据,最后实现机载重轨InSAR图像三维定位的方法。通过重采样辅图像,获得像元一一对应的InSAR图像对,使得图像对之间的相对定位更加精确。相干性更加良好,干涉处理后获得高精度的DEM。实验结果表明本文方法可以实现机载重轨InSAR图像高精度三维定位。但是,本文试验数据是正侧视模型下的成像数据,还需验证对斜侧视模型下成像数据的处理效果。试验区域地形平坦,无需外源DEM辅助,在地形复杂地区需要引入外源DEM辅助处理[20]。另外,本文未考虑大气效应[21-22]和土壤含水量[23]的影响,且本文方法对于长条带的重轨机载InSAR图像的有效性,还需进一步试验。
| [1] |
岳昔娟.稀少(无)控制条件下机载SAR高精度定位技术研究[D].武汉: 武汉大学, 2009.
|
| [2] |
杨杰, 潘斌, 李德仁, 等. 无地面控制点的星载SAR影像直接对地定位研究[J]. 武汉大学学报(信息科学版), 2006, 31(2): 144-147. |
| [3] |
Raney R K, Runge H, Bamler R, et al. Precision SAR processing using chirp scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 786-799. Doi:10.1109/36.298008 |
| [4] |
Carrara W G, Goodman R S. Majewski R M. Spotlight synthetic aperture radar: signal processing algorithms[M]. Boston: Artech House, 1995: 597-598.
|
| [5] |
Cumming I G, Wong F H. Digital processing of synthetic aperture radar data:algorithms and implementation[M]. London: Artech House, 2007.
|
| [6] |
Perissin D, Wang T. Repeat-Pass SAR interferometry with partially coherent targets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 50(1): 271-280. |
| [7] |
钟雪莲, 向茂生, 郭华东, 等. 机载重轨干涉合成孔径雷达的发展[J]. 雷达学报, 2016, 2(3): 367-381. |
| [8] |
黄国满, 张继贤, 赵争, 等. 机载InSAR测绘制图应用系统研究[J]. 测绘学报, 2008, 37(3): 277-279. Doi:10.3321/j.issn:1001-1595.2008.03.003 |
| [9] |
黄国满, 岳昔娟, 赵争, 等. 基于多项式正射纠正模型的机载SAR影像区域网平差[J]. 武汉大学学报(信息科学版), 2008. |
| [10] |
Konecny G, Schuhr W. Reliability of radar image data[J]. ISPRS Comm. I Symposium, 1988, 27(B1): 456-469. |
| [11] |
Curlander J C. Location of pixels in space-borne SAR imagery[J]. IEEE Transaction on Geoscience and Remote Sensing, 1982, 20(3): 359-364. |
| [12] |
潘志刚, 潘卓, 曹舸. 机载SAR图像无控制点直接定位方法[J]. 中国科学院大学学报, 2015, 32(4): 587-541. |
| [13] |
Johnsen H, Lauknes L, Guneriussen T. Geocoding of fast-delivery ESR-1SAR image mode product using DEM data[J]. International Journal of Remote Sensing, 1995, 16(11): 1957-1968. Doi:10.1080/01431169508954532 |
| [14] |
岳昔娟, 黄国满, 赵争. 机载SAR影像主动定位的数学模型研究[J]. 测绘科学, 2009, 34(supp1): 181-183. |
| [15] |
吴颖丹. 基于R-D模型的星载SAR影像直接目标定位[J]. 湖北工业大学学报, 2012, 27(5): 40-45. Doi:10.3969/j.issn.1003-4684.2012.05.011 |
| [16] |
刘佳音, 韩冰, 洪文. 一种新的SAR图像斜距多普勒定位模型的直接解法[J]. 遥感技术与应用, 2012, 27(5): 716-721. |
| [17] |
张红敏, 靳国旺, 徐青, 等. 基于DEM和图像仿真的单幅SAR图像无控制定位[J]. 测绘科学技术学报, 2013, 30(3): 274-278. Doi:10.3969/j.issn.1673-6338.2013.03.013 |
| [18] |
张红敏, 靳国旺, 徐青, 等. 利用单个地面控制点的SAR图像高精度立体定位[J]. 雷达学报, 2014, 3(1): 85-91. |
| [19] |
邱春平, 张红敏, 靳国旺, 等. 机载SAR影像距离-斜视角模型立体定位[J]. 测绘科学技术学报, 2014, 31(4): 399-402. Doi:10.3969/j.issn.1673-6338.2014.04.015 |
| [20] |
唐晓青, 向茂生, 吴一戎. 一种改进的基于DEM的机载重轨InSAR运动补偿算法[J]. 电子与信息学报, 2009, 31(5): 1090-1094. |
| [21] |
薛东剑, 郑洁, 李成绕, 等. 利用L波段星载重复轨道InSAR提取DEM及大气效应分析[J]. 测绘工程, 2018, 27(1): 5-14. |
| [22] |
李文梅.极化InSAR层析估测森林垂直结构参数方法研究[D].北京: 中国林业科学研究院, 2013.
|
| [23] |
赵少华, 秦其明, 沈心一, 等. 微波遥感技术监测土壤湿度的研究[J]. 微波学报, 2010, 26(2): 90-96. |
 2019, Vol. 36
2019, Vol. 36 


