2. Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology(CICAEET), Nanjing 210044, China;
3. College of Physics and Electronic Engineering, Xinjiang Normal University, Urumqi 830054, China
2. 江苏省大气环境与装备技术协同创新中心, 南京 210044;
3. 新疆师范大学物理与电子工程学院, 乌鲁木齐 830054
The large family of VOCs contains mainly hydrocarbons, aldehydes, ketones, etc. These compounds have different contribution rates in emission source and have different reactivities in the atmosphere[1]. While the halogenated hydrocarbon compounds enter the atmosphere, the photochemical reactions take place under the irradiation of sunlight. The halogen atoms produced by photolysis catalyze the decomposition of ozone, posing a great threat to the life on the earth[2]. Therefore, the degradation of halogenated hydrocarbon compounds has attracted widespread attention. As a kind of halogenated hydr-ocarbons, bromoethane dissociates under the radi-ation of sunlight and generates the bromine radical, which severely damages the atmospheric ozone layer.
Several methods have been applied to dissociate the bromoethane, including microbial degradation, photocatalytic degradation, ultrasonic degradation, and electrochemical degradation, and they have different advantages and disadvantages in their applications. The degradation of pollutants under external electric fields is a promising new method[3-4] and a hot spot in current researches[5-7]. The physical properties and dissociation characteristics of bromoethane under external electric fields have not yet been studied.
In this paper, the structure and the spectral and dissociation properties of bromoethane under external field have been calculated by using the density functional theory. The geometric structure, bond lengths, dipole moments, vibration frequ-encies, and other physical parameters are obtained. Meanwhile the potential energy curves under diff-erent external electric fields are obtained by scan-ning the single point energy along the C—Br bond.
1 Theory and computational methodThe Hamiltonian of the molecule under external electric field is
| $ H = {H_0} + {H_{{\mathop{\rm int}} }}, $ | (1) |
where H0 is the Hamiltonian of the molecule without the external field, and Hintis the interaction Hamiltonian between the external electric field and the molecular system.
Using the dipole approximation, the interaction Hamiltonian can be expressed as
| $ {H_{{\rm{int}}}} = - \mu \cdot F, $ | (2) |
where μ is the dipole moment and F represents the external electric field[8] (a.u. stands for atomic units, 1 a.u.=5.142 25×1011 V·m-1).
Gaussian 09[9] is used to carry out the theoretical calculations. First, the structure of bromoethane as shown in Fig. 1, has been optimized with different methods. By comparing the calculated data in Table 1 with the experimental values, we find that the calculation results at the B3LYP/6-31G+(d, p) level are in the best agreement with the experimental values. So, the B3LYP/6-31G+(d, p) level is used in further calculations for the total energy, dipole moment, frontier orbital levels, IR spectra, and potential energy curves.

|
Download:
|
|
Fig. 1 The optimized geometry of the ground-state bromoethane |
|
|
|
Table 1 The ground-state structure parameters of bromoethane obtained using different optimization methods |
When different electric fields are applied in the x-axis or y-axis direction, the degradation effect is less important than in the z-axis direction. Thus, in this study, bromoethane is exposed under different external electric fields along the z-axis.
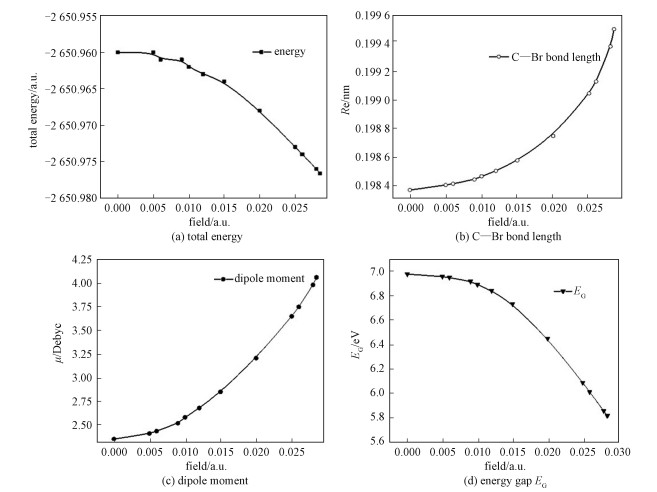
The calculated results for the bond length (C—Br), total energy, and electric dipole moment under different external electric fields (0-0.028 5 a.u.) are shown in Fig. 2.
|
Download:
|
|
Fig. 2 Calculated physical characteristics of bromoethane under different electric fields |
|
As shown in Fig. 2, the total energy decreases when the external electric field gradually increases, and the C—Br bond becomes longer in this process, which indicates that the C—Br bond is apt to break. At the same time, the dipole moment increases sharply, which means the molecule is splitting up.
2.2 Effects of external electric fields on molecular orbital energy level distributionThe total energies, the lowest unoccupied molecule orbital (LUMO) energy EL, the highest occupied molecule orbital (HOMO) energy EH, and the energy gap EH of bromoethane under different external fields were also obtained. The energy gap EG is given as
| $ {E_{\rm{G}}} = \left( {{E_{\rm{L}}} - {E_{\rm{H}}}} \right) \times 27.2{\rm{eV}}{\rm{.}} $ | (3) |
It shows that the energy gap decreases monotonously while the external field increases from 0 to 0.028 5 a.u., as shown in Fig. 2 (d). This result indicates that the bromoethane molecule is more easily excited to a higher state.
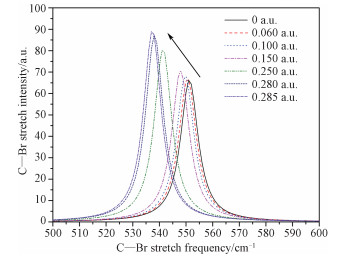
2.3 Effects of external electric fields on IR spectrumThe infrared spectra of bromoethane under different external electric fields are also obtained. Bromoethane has eighteen different vibration modes. The calculated spectrum of the C—Br str (the calculated frequency of the C—Br str is 551 cm-1 under zero external fields, which is in good agreement with the experimental values[12-13]) under different external fields is shown in Fig. 3. It is seen that the frequency of the C—Br str shows red shift while the external field increases.
|
Download:
|
|
Fig. 3 The change of the C—Br stretch spectrum with the increase of external electric field |
|
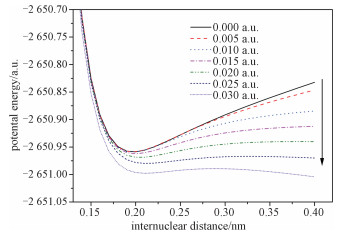
wBy scanning single point energies along the C—Br distance, the potential energy curves under different external electric fields are obtained at the B3LYP/6-31+G(d, p) level (see Fig. 4). To smooth the curves, the results are fitted by the Morse potential model[15]
|
Download:
|
|
Fig. 4 The dissociation PESS (potential energy surfaces) along the C—Br bond of bromoethane under external electric fields |
|
| $ V(\gamma ) = {D_{\rm{e}}}{\left[ {1 - {{\rm{e}}^{ - a\left( {\gamma - {R_{\rm{e}}}} \right)}}} \right]^2}, $ | (4) |
where De is the dissociation energy, a is the Morse parame ter, γ is the internuclear distance, and Re is the equilibrium distance.
It is seen that the molecule stays in a stable point without external fields. However, the barrier of the dissociation of bromoethane drops significantly while the external field increases. When the external electric field reaches to 0.030 a.u., the barrier of the dissociation of bromoethane disappears completely, which demonstrates that the C—Br bond breaks and bromoethane is degraded under 0.030 a.u.. The results provide important information for studying the degradation mechanism of bromoethane under different external electric fields.
3 ConclusionsIn the present work, the spectral and dissociation properties of bromoethane under external electric fields(0-0.028 5 a.u.) are calculated. The density functional theory at the B3LYP/6-31G+(d, p) level is employed.
It is seen that the structure properties and the spectral and dissociation characteristics of brom-oethane are quite interesting under different external electric fields.
The results show that the total energy decreases as the external electric field gradually increases. The C—Br bond becomes longer in this process, which implies that the C—Br bond is apt to break. At the same time, the dipole moment inereases sharply, which means the molecule is splitting up. Meanwhile, the energy gap decreases monotonously and the C—Br strfrequency shows red shift while the external field increases.
It is shown that the dissociation barrier of bromoethane drops significantly while the external field increases. When the external electric field meaches to 0.030 a.u., the dissociation barrier of bromoethane disappears completely, which demon-strates that the C—Br bond breaks and bromoethane is degraded under 0.030 a.u.. The results provide important information for studying the degradation of bromoethane under different external electric fields.
| [1] |
Mo Z W, Shao M, Lu S H. Review on volatile organic compounds (VOCs) source profiles measured in China[J]. Acta Scientiae Circumstantiae, 2014, 34(9): 2179-2189. |
| [2] |
Liu J L. Degrdation mechanisms and kinetic studies on he halogenated hydrocarbon in the atmosphere[D]. Lanzhou: Northwest Normal University, 2013(in Chinese).
|
| [3] |
Liu Y Z, Li X H, Wang J F, et al. Study on dissociation properties and spectra of halon 1301 in external electric field[J]. Spectrosc Spect Anal, 2017, 37(3): 679-684. |
| [4] |
Ling Z G, Tang Y L, Li Y P, et al. Molecular structure and electronic spectrum of 2, 2', 5, 5'-tetrachlorobiphenyl under the external electric field[J]. Acta Phys Sin, 2013, 62(22): 133-140. |
| [5] |
Sidir I, Sidir Y G, Berber H, et al. Emerging ground and excited state dipole moments and external electronic structure:a solvatochromism and theoretical study on 2-((phenylimino)-methyl)phenol derivatives[J]. Mol Liq, 2015, 206: 56-67. DOI:10.1016/j.molliq.2015.01.056 |
| [6] |
Setayandeh S S, Lohrasebi A. The effects of external electric fields of 900 MHz and 2450 MHz frequencies on αβ-tubulin dimer stabilized by paclitaxel:molecular dynamics approach[J]. Theor Comput Chem, 2016, 15(2): 1650010. DOI:10.1142/S0219633616500103 |
| [7] |
Sajadi M, Lohrasebi A, Setayandeh S S, et al. Water molecules response to an external GHz electric field in KcsA potassium channel:a molecular modeling approach[J]. Theor Comput Chem, 2015, 14(2): 1550012. DOI:10.1142/S0219633615500121 |
| [8] |
Cooper G, Olney T N, Brion C E. Absolute UV and Soft X-ray photoabsorption of ethylene by high resolution dipole (e, e) spectroscopy[J]. Chem Phys, 1995, 194(1): 175-184. |
| [9] |
Frish M J, Trucks G W, Schlegel H B, et al. Gaussian 09, Revision C.01[CP]. Walling ford: Gaussian Inc, 2010.
|
| [10] |
Flanagan C, Pierce L. Microwave spectrum, structure, and quadrupole coupling constant tensor of ethyl bromide[J]. Chem Phys, 1963, 38(12): 2963. |
| [11] |
Kudchadker S A, Kudchadker A P. Ideal gas thermodynamic properties of selected bromoethanes and iodoethane[J]. Chem Phys, 1979, 8(2): 519. |
| [12] |
Experimental IR spectrum of Bromoethane. NIST chemical kinetic data base[EB/OL].[2018-03-10]. http://webbook.nist.gov/cgi/cbook.cgi?ID=C74964&Units=SI&Type=IR-SPEC&Index=0#IR-SPEC.
|
| [13] |
Zhang Y P, Wang H T, Zhang L, et al. Measurements of IR absorption across section and spectrum simulation of lewisite[J]. Spectrosc Spect Anal, 2015, 35(2): 466-469. |
| [14] |
Irikura K K, Johnson R D, Kacker R N. Uncertainties in scaling factors for ab initio vibrational frequencies[J]. Phys Chem A, 2005, 109: 8430-8437. DOI:10.1021/jp052793n |
| [15] |
Zhu Z H, Yu H G. Molecular structure and potential energy function[M]. Beijing: Science Press, 1997.
|
 2019, Vol. 36
2019, Vol. 36 


