以第3代自动链路建立3G-ALE(Third-Generation Automatic Link Establishment)技术为基础的第3代短波自适应通信,因其良好的通信性能而被广泛应用于美军与北约军事通信中[1]。
在通信对抗行动中,信号检测及其参数估计是实施通信干扰的基础。但是由于实际对抗行动的非合作性,截获到的3G-ALE信号往往信噪比较低,并且在频域易受到短波信道影响而产生载频频偏,使得信号检测面临巨大困难。基于信号8PSK(Phase Shift Keying)调制样式的检测方法,如特征参数检测[2]、高阶累积量检测[3]等,受噪声影响大,低信噪比条件下的检测性能不佳,并且只能够检测信号调制样式,无法判断其是否为3G-ALE信号。利用位于信号前端并且公开的探测报头进行相关检测,能够较好地克服该问题,较为典型的是滑动相关FFT(Fast Fourier Transform)检测方法[4-5],在检测3G-ALE信号的同时还能够实现载频估计,但是该方法同样存在低信噪比导致相关FFT检测谱峰被淹没、检测性能下降的问题。混沌检测是一种目前正在迅猛发展的能够在低信噪比条件下有效检测微弱信号的新方法,相比传统方法具有更好的信号检测性能[6-10]。但是混沌检测只对同频信号敏感,然而3G-ALE信号经过信道传输后往往会产生载频频偏,使得需要通过不断调整混沌振子内置参数或者使用混沌阵实现信号的检测与载频估计[11-12],这样就降低了混沌检测方法的时效性并且增加了复杂度,不利于工程实现。
本文针对传统检测方法与常规混沌检测方法的不足,提出一种基于Duffing混沌振子的短波3G-ALE信号多通道检测方法,能够实现低信噪比、载频频偏条件下的信号检测与载频估计。首先利用探测报头对截获信号滑动相关预处理;然后将相关运算信号分别输入至多路检测通道,每路检测通道中使用不同角频率本振将相关运算信号搬移至相同Duffing混沌振子周期策动力角频率附近;由于振子对同频信号的敏感性,只有当本振搬移后的角频率与周期策动力角频率一致或者相差很小时,振子输出状态发生变化,据此判定检测到截获信号中3G-ALE信号的存在,并根据振子所在检测通道的本振角频率推算载频频偏,进而估计出信号载频。该方法避免了对Duffing混沌振子内置参数的调整,一定程度上降低了常规混沌检测方法的复杂度,理论分析与仿真实验验证了该方法对于3G-ALE信号检测与载频估计的有效性。
1 短波3G-ALE信号模型3G-ALE信号一般包含保护序列(TLC/AGC,Transmit Level Control/Automatic Gain Control)、探测报头序列(PRE,Preamble)与有效载荷数据序列(DATA)等3个信号部分[13]。其中,保护序列用于通信发送端的发送电平控制与通信接收端的自动增益控制;探测报头序列用于信号的检测、参数估计、同步等预处理;有效载荷数据序列用于携带特定交互作用的链路层协议信息。图 1所示为3G-ALE信号用于自动链路建立ALE协议的突发波形BW0(No.0 Burst Waveform)信号结构。

|
Download:
|
| 图 1 突发波形BW0信号结构 Fig. 1 Signal structure of the burst waveform BW0 | |
美军标MIL-STD-188-141B规定了3G-ALE信号突发波形BW0中的探测报头是384符号八进制序列[13],即
7 7 7 7 5 4 3 1 1 2 0 2 7 2 2 0 1 3 4 7 5 3 7 7 4 3 1 0 1 1 5 2 1 6 0 0 4 7 6 2 2 3 6 0 5 1 7 6 1 6 1 7 6 6 6 1 7 3 0 4 7 1 2 2 3 3 6 7 7 1 7 3 1 5 0 3 3 4 5 2 5 2 5 3 1 7 2 1 5 7 6 1 2 5 3 5 3 6 2 0 7 5 6 6 0 1 4 2 5 4 1 1 7 0 0 6 6 7 5 6 3 7 4 0 2 6 3 6 4 5 1 0 0 4 5 5 4 7 1 5 1 5 6 7 3 3 5 2 2 2 7 2 3 3 0 4 1 4 1 3 6 0 7 2 6 1 5 0 1 4 1 1 7 0 7 4 0 2 4 5 3 0 0 3 1 2 6 4 6 5 2 6 0 0 7 3 5 3 4 0 6 2 7 4 3 3 7 6 7 1 0 0 6 7 3 1 5 5 0 2 3 4 2 7 7 4 5 2 1 6 1 0 4 7 1 6 1 2 4 0 3 6 5 4 5 4 4 6 1 2 5 1 3 6 2 7 2 6 7 4 7 3 0 1 5 0 5 3 4 5 0 7 3 2 7 0 3 2 7 0 6 1 6 7 7 1 4 2 6 7 7 4 2 7 2 7 3 7 6 3 2 6 5 6 6 3 6 6 4 1 0 6 2 6 4 1 5 5 4 3 3 4 6 3 5 2 4 1 1 7 5 3 7 1 6 5 4 6 6 2 3 4 2 3 3 7 4 1 4 4 5 4 6 1 3 4 6 1 7 4 1 3 5 2 6 5 5 4 2 1 5 1 6 1 2 7 1 4 4 2 3 4 7 3
只考虑探测报头部分,通信发送端的3G-ALE信号可以表示为
| $ s\left( t \right) = \exp \left[ {{\rm{j}}\varphi \left( t \right)} \right]\exp \left( {{\rm{j}}{\omega _{\rm{c}}}t} \right), $ | (1) |
式中:φ(t)为探测报头序列映射的相位信息;ωc为发送信号射频载波角频率。令
| $ p\left( t \right) = \exp \left[ {{\rm{j}}\varphi \left( t \right)} \right] $ | (2) |
表示受到探测报头序列调制的8PSK基带探测报头信号,则发送信号s(t)可以简化为
| $ s\left( t \right) = p\left( t \right)\exp \left( {{\rm{j}}{\omega _{\rm{c}}}t} \right). $ | (3) |
3G-ALE信号经过信道传输,不仅会受到加性高斯白噪声的影响,还由于多普勒效应而产生载频频偏。通信对抗方截获信号可以表示为
| $ \begin{array}{l} r\left( t \right) = s\left( t \right)\exp \left( {{\rm{j}}{\omega _{\rm{s}}}t} \right) + n\left( t \right)\\ \;\;\;\;\;\;\; = p\left( t \right)\exp \left( {{\rm{j}}{\omega _{\rm{r}}}t} \right) + n\left( t \right), \end{array} $ | (4) |
式中:ωs为载频频偏;ωr=ωc+ωs为截获信号中3G-ALE信号射频载波角频率;n(t)为信道零均值加性高斯白噪声。
2 基于Duffing混沌振子的多通道检测 2.1 Duffing混沌检测原理适用于信号混沌检测的Holmes改进型Duffing振子方程[14-15]为
| $ x'' = - k\omega x' + {\omega ^2}\left[ { - \left( { - {x^3} + {x^5}} \right) + \gamma \cos \left( {\omega t} \right)} \right]. $ | (5) |
式中:x是关于变量t的函数,x′、x″分别是x的一阶导函数、二阶导函数;k为Duffing混沌振子阻尼比,通常将其取值为0.5;-x3+x5为振子非线性恢复力;单音信号γcos(ωt)为振子周期策动力,ω为策动力角频率,γ为策动力幅度。式(5)也可以改写为
| $ \left\{ {\begin{array}{*{20}{l}} {x' = \omega y}\\ {y' = \omega \left[ { - ky - \left( { - {x^3} + {x^5}} \right) + \gamma \cos \left( {\omega t} \right)} \right]} \end{array}} \right.. $ | (6) |
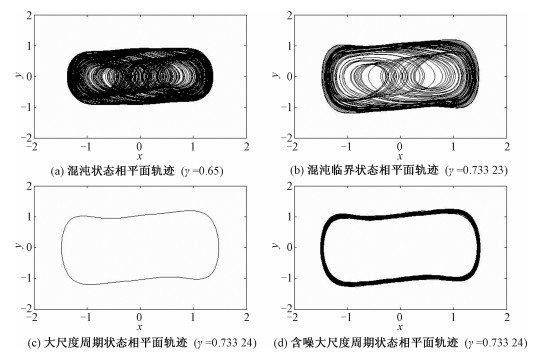
对于策动力角频率ω预先设置为ωd值的某一Duffing混沌振子,振子输出x、y的相平面轨迹随着策动力幅度γ的增大而逐渐演变为混沌状态(如图 2(a)所示),并且在较大范围内保持该状态;当γ增大到某一临界值γd时,振子输出处于混沌临界状态(如图 2(b)所示);此时如果γ继续增大,振子输出将跃迁为大尺度周期状态(如图 2(c)所示),而这种状态变化即使是γ的微小增大也能够导致,即振子对微弱单音信号敏感。
|
Download:
|
| 图 2 Duffing混沌振子输出状态变化 Fig. 2 Changes of Duffing chaotic oscillator's output state | |
当Duffing混沌振子的周期策动力受到噪声影响时,上述状态变化依然存在,并且当处于大尺度周期状态时,振子对噪声具有免疫性[14],即噪声的存在不改变振子输出状态,仅仅使得状态轨迹不再平滑、出现毛刺(如图 2(d)所示)。利用Duffing混沌振子对微弱单音信号敏感、对噪声免疫的特性,建立信号的混沌检测模型
| $ \begin{array}{l} x'' = - k{\omega _{\rm{d}}}x' + \\ \;\;\;\;\;\;\omega _{\rm{d}}^2\left[ { - \left( { - {x^3} + {x^5}} \right) + {\gamma _{\rm{d}}}\cos \left( {{\omega _{\rm{d}}}t} \right) + i\left( t \right)} \right], \end{array} $ | (7) |
式中:ωd、γd为Duffing混沌振子内置参数,并且γd通常随ωd而改变;i(t)为振子输入信号。根据内置参数ωd调整γd,使得振子输出处于混沌临界状态,此时若输入i(t)中存在角频率ωd的单音信号,则振子输出将跃迁为大尺度周期状态,据此判定检测到该单音信号的存在。
2.2 3G-ALE信号的混沌检测在自动链路建立过程中,通信发送端持续发送突发波形BW0的3G-ALE信号,这就为通信对抗方检测信号的存在提供了可能。
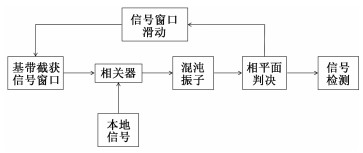
将Duffing混沌检测原理应用于3G-ALE信号,检测思路如图 3所示。
|
Download:
|
| 图 3 3G-ALE信号混沌检测思路 Fig. 3 Thought of chaotic detection for 3G-ALE signal | |
Duffing混沌振子内置参数预先设置为ωd、γd。
对式(4)的通信对抗方截获信号r(t)去载波,得到基带截获信号。暂不考虑载频频偏ωs,则有
| $ \begin{array}{l} {r_1}\left( t \right) = r\left( t \right)\exp \left( { - {\rm{j}}{\omega _{\rm{c}}}t} \right)\\ \;\;\;\;\;\;\; = \left[ {p\left( t \right)\exp \left( {{\rm{j}}{\omega _{\rm{c}}}t} \right) + n\left( t \right)} \right]\exp \left( { - {\rm{j}}{\omega _{\rm{c}}}t} \right)\\ \;\;\;\;\;\;\; = p\left( t \right) + n\left( t \right)\exp \left( { - {\rm{j}}{\omega _{\rm{c}}}t} \right). \end{array} $ | (8) |
将公开的探测报头按照MIL-STD-188-141B军标规定的信号格式调制产生8PSK基带本地信号p(t);在基带截获信号内从截获起始时刻开始,取一段与基带本地信号p(t)长度相一致的信号窗口w(t),并向后滑动信号窗口;将基带本地信号p(t)取共轭后与信号窗口w(t)做相关运算。假设此时的信号窗口已经滑动至基带截获信号中3G-ALE信号探测报头位置,即w(t)=r1(t),则有
| $ \begin{array}{l} {r_2}\left( t \right) = w\left( t \right){p^*}\left( t \right)\\ \;\;\;\;\;\;\; = {r_1}\left( t \right){p^*}\left( t \right)\\ \;\;\;\;\;\;\; = p\left( t \right){p^*}\left( t \right) + n\left( t \right){p^*}\left( t \right)\exp \left( { - {\rm{j}}{\omega _{\rm{c}}}t} \right). \end{array} $ | (9) |
将相关运算信号r2(t)通过本振搬移至预先设置的Duffing混沌振子周期策动力角频率ωd处:
| $ \begin{array}{l} {r_3}\left( t \right) = {r_2}\left( t \right)\exp \left( {{\rm{j}}{\omega _{\rm{d}}}t} \right)\\ \;\;\;\;\;\;\; = p\left( t \right){p^*}\left( t \right)\exp \left( {{\rm{j}}{\omega _{\rm{d}}}t} \right) + \\ \;\;\;\;\;\;\;\;n\left( t \right){p^*}\left( t \right)\exp \left[ {{\rm{j}}\left( {{\omega _{\rm{d}}} - {\omega _{\rm{c}}}} \right)t} \right], \end{array} $ | (10) |
考虑到式(10)中第1项:
| $ p\left( t \right){p^*}\left( t \right) = \exp \left[ {{\rm{j}}\varphi \left( t \right)} \right]\exp \left[ { - {\rm{j}}\varphi \left( t \right)} \right] = \mathit{\boldsymbol{1}}, $ | (11) |
则可以将式(10)改写为
| $ \begin{array}{l} {r_3}\left( t \right) = \exp \left( {{\rm{j}}{\omega _{\rm{d}}}t} \right) + \\ \;\;\;\;\;\;\;\;\;\;n\left( t \right){p^*}\left( t \right)\exp \left[ {{\rm{j}}\left( {{\omega _{\rm{d}}} - {\omega _{\rm{c}}}} \right)t} \right], \end{array} $ | (12) |
式中:第1项为角频率ωd的单音信号项,第2项为噪声项。因此将信号r3(t)取实部分量后作为式(7)中混沌振子的输入i(t),就可以判定检测到单音信号exp(jωdt)的存在,亦即截获信号中3G-ALE信号的存在。
然而实际3G-ALE信号经过信道传输后往往会产生载频频偏ωs,导致式(12)中第1项的单音信号变为exp[j(ωd+ωs)t],其角频率与Duffing混沌振子周期策动力角频率ωd不一致。由于振子对角频率相差较大的单音信号同样具有免疫性[14],使得上述混沌检测方法不再可行。
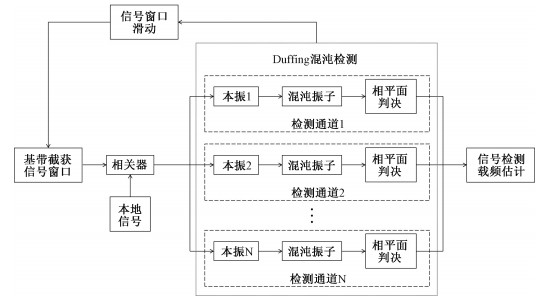
2.3 多通道检测方法与分析针对载频频偏条件下3G-ALE信号混沌检测存在的问题,常规改进方法是不断调整混沌振子内置参数或者使用混沌阵,通过不同内置参数的振子以匹配不同角频率的输入信号,这样就使得混沌检测方法的复杂度大大增加,同时检测时效性被降低。本节提出一种克服该问题的多通道检测方法,如图 4所示。
|
Download:
|
| 图 4 3G-ALE信号多通道检测方法 Fig. 4 Multichannel detection method for 3G-ALE signal | |
首先对截获信号r(t)做相同的滑动相关预处理,得到如下相关运算信号
| $ {r_2}\left( t \right) = \exp \left( {{\rm{j}}{\omega _{\rm{s}}}t} \right) + n\left( t \right){p^*}\left( t \right)\exp \left( { - {\rm{j}}{\omega _{\rm{c}}}t} \right), $ | (13) |
将其分别输入至N路检测通道,每路检测通道中使用不同角频率的本振。第n路检测通道中经过本振角频率搬移后的信号表达式为
| $ \begin{array}{l} {r_{3,n}}(t) = {r_2}(t)\exp \left( {{\rm{j}}{\omega _n}t} \right)\\ \;\;\;\;\;\;\;\; = \exp \left[ {{\rm{j}}\left( {{\omega _n} + {\omega _{\rm{s}}}} \right)t} \right] + \\ \;\;\;\;\;\;\;\;\;\;n\left( t \right){p^*}\left( t \right)\exp \left[ {{\rm{j}}\left( {{\omega _n} - {\omega _{\rm{c}}}} \right)t} \right], \end{array} $ | (14) |
式中:ωn为第n路检测通道的本振角频率。之后分别输入至各自检测通道的Duffing混沌振子,每路检测通道的混沌振子预先设置有相同的内置参数ωd、γd。当检测通道
| $ {\omega _{\rm{s}}} = {\omega _{\rm{d}}} - {\omega _{\hat n}}, $ | (15) |
进一步估计出截获信号中3G-ALE信号射频载波角频率
| $ {\omega _{\rm{r}}} = {\omega _{\rm{c}}} + {\omega _{\rm{s}}} = {\omega _{\rm{c}}} + \left( {{\omega _{\rm{d}}} - {\omega _{\hat n}}} \right). $ | (16) |
文献[16-17]指出,Duffing混沌振子输入不同角频率的单音信号时,输入信号角频率与振子周期策动力角频率的差值Δωn=ωd-(ωn+ωs)影响振子输出x的方差。当二者角频率相一致即Δω=0时,振子输出x的方差达到最大值。因此,多通道检测的3G-ALE信号载频估计可以表示为
| $ {\omega _{\rm{r}}} = {\omega _{\rm{c}}} + \left( {{\omega _{\rm{d}}} - {\omega _{\hat n}}} \right)|\hat n = \mathop {\rm argmax}\limits_{n = 1,2, \cdots ,N} \;{\rm var}\left( {{x_n}} \right), $ | (17) |
式中:xn为第n路检测通道混沌振子的输出x;var(·)表示方差计算。
3 仿真实验本节以通信对抗方截获信号中3G-ALE信号的检测概率与载频估计误差作为检测性能指标,仿真提出的基于Duffing混沌振子的多通道检测实验。仿真实验参数设置如表 1所示。
|
|
表 1 仿真实验参数设置 Table 1 Parameters setting for simulation experiment |
仿真实验的Duffing混沌振子内置参数做以下设置:混沌振子阻尼比k=0.5,周期策动力角频率ωd=2π×100 rad/s,通过计算机双精度运算可求得对应周期策动力幅度临界值γd=0.733 23。Duffing振子方程的求解采用4阶Runge-Kutta算法,求解初值[x(0), y(0)]=[0, 0],求解步长h=1/9 600。
定义信道信噪比
| $ {\rm{SNR}} = 10\lg \left( {\frac{{{P_{\rm{s}}}}}{{{P_{\rm{n}}}}}} \right)\left( {{\rm{dB}}} \right), $ | (18) |
表示在通信对抗方截获信号中存在3G-ALE信号的前提下,3G-ALE信号功率Ps与信道零均值加性高斯白噪声功率Pn的比值,亦即通信对抗方截获信号信噪比。
3.1 信号检测效果实验本节在0~10 Hz范围内任意载频频偏的条件下,比较提出的基于Duffing混沌振子的多通道检测方法与滑动相关FFT检测、高阶累积量检测、特征参数检测等传统检测方法,对于截获信号中3G-ALE信号的检测效果。
其中,滑动相关FFT检测是对滑动相关预处理得到的相关运算信号r2(t)进行FFT变换后求其最大相关FFT检测谱峰,高阶累积量检测是对基带截获信号r1(t)求归一化的4阶累积量对角切片,特征参数检测是对相关运算信号r2(t)求归一化的瞬时功率谱密度最大值。
定义检测概率:在通信对抗方截获信号中存在3G-ALE信号的前提下,Monte Carlo实验检测信号存在的次数与Monte Carlo实验次数的比值。
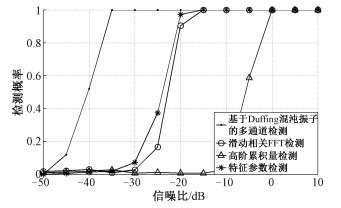
图 5对比显示不同检测方法的检测效果。
|
Download:
|
| 图 5 不同检测方法检测效果对比 Fig. 5 Comparison of detection effect among different methods | |
实验结果表明,基于Duffing混沌振子的多通道检测方法优势明显,大大提高了低信噪比条件下的3G-ALE信号检测性能。即使当截获信号信噪比低至-35 dB时,方法仍能够实现有效检测,并且相比高阶累积量检测方法具有高达35 dB左右的性能优势,而与滑动相关FFT检测方法和特征参数检测方法相比也具有约15 dB的性能优势。
3.2 信号载频估计效果实验本节在0~10 Hz范围内任意载频频偏的条件下,比较提出的基于Duffing混沌振子的多通道检测方法与滑动相关FFT检测方法,对于截获信号中3G-ALE信号的载频估计效果。由于实验设置最大载频频偏为10 Hz,为减少仿真实验的运行时间,仅设置方法中的检测通道数量为11路,每路检测通道的本振角频率间隔2π×1 rad/s,因此检测通道的本振角频率覆盖范围2π×(90~100) rad/s,相应地可估计副载频范围1 800~1 810 Hz。
定义载频估计误差:在通信对抗方截获信号中存在3G-ALE信号并且已检测信号存在的前提下,Monte Carlo实验得到的副载频估计误差平均值。
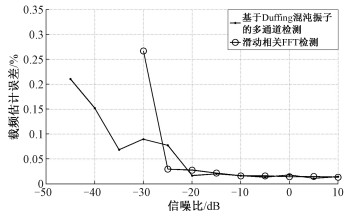
图 6对不同检测方法的载频估计效果进行对比显示。
|
Download:
|
| 图 6 不同检测方法载频估计效果对比 Fig. 6 Comparison of estimation effect on carrier frequency between the two detection methods | |
实验结果表明,基于Duffing混沌振子的多通道检测方法能够实现对截获信号中3G-ALE信号射频载波角频率的有效估计,在低信噪比条件下仍能保持较小的载频估计误差。滑动相关FFT检测方法则由于相关FFT检测谱峰被噪声所淹没,载频估计效果出现恶化,甚至当信噪比低至-30 dB以下时,由于已无法有效检测到截获信号中3G-ALE信号的存在,也就无法对信号载频进行估计。
3.3 综合分析与思考本文提出的多通道检测方法,优势在于是使用固定内置参数的Duffing混沌振子,检测过程中不需要对其进行调整,也就不需要确定多组振子内置参数,增加方法复杂度的仅是混沌检测前端不同角频率的本振。常规混沌检测方法则是使用内置参数变化的混沌振子或者是建立混沌阵,这就要求确定数量较多的振子内置参数,并在检测过程中不断对其进行调整或者是在混沌阵中设置不同内置参数的振子,因此额外增加了混沌检测方法的复杂度,其实现也较为困难[18]。
实验设置最大载频频偏为10 Hz,但是在实际应用中是无法事先知道信号载频频偏的,这就给多通道检测方法的检测通道数量设置造成了困难。事实上,常规混沌检测方法同样存在不同内置参数的混沌振子数量设置不确定的类似问题,文献[18]为提高检测精度,仅在周期策动力角频率2π×10 rad/s的调整范围内就设置了79个振子。本文中所采取的解决措施是根据短波信道传输产生多普勒频偏的典型值设置检测通道数量,文献[19]指出,短波信道传输产生的多普勒频偏仅为几赫兹,因此可以通过适当增加检测通道数量,细化每路检测通道的本振角频率间隔,以进一步提高混沌检测分辨率,进而提高信号检测概率并降低载频估计误差。
4 总结针对非合作通信对抗方在低信噪比、载频频偏条件下,传统方法检测短波3G-ALE信号的困难,提出一种基于Duffing混沌振子的多通道检测方法。理论分析与仿真实验验证了方法对于3G-ALE信号检测与载频估计的有效性,并且一定程度上降低了常规混沌检测方法的复杂度,为实际工程应用提供了参考借鉴。本文仅根据经验值来设置方法所需检测通道的数量,研究检测通道数量合理设置的问题将是下一步工作的重点。
| [1] |
Johnson E E. Analysis of third-generation HF ALE technologies[C]//21st Century Military Communications Conference. Los Angeles, CA, USA: IEEE, 2000: 1139-1143.
|
| [2] |
吴迪, 葛临东, 王彬. 短波突发信号盲检测算法的对比研究[J]. 通信学报, 2010, 31(8A): 111-116. |
| [3] |
黄飞翔.低信噪比突发通信中信号捕获的研究与实现[D].成都: 电子科技大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10614-1015709064.htm
|
| [4] |
徐宝.短波第三代通信信号解调算法研究[D].广州: 华南理工大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10561-1015987714.htm
|
| [5] |
Saraswathi K, Ravishankar S. Efficient estimation and compensation of Doppler shift for OFDM signals in underwater communications[C]//Sixth International Symposium on Embedded Computing and System Design. Patna, India: IEEE, 2016: 137-141.
|
| [6] |
Wang G Y, He S L. A quantitative study on detection and estimation of weak signals by using chaotic Duffing oscillators[J]. IEEE Transactions on Circuits and Systems-I:Fundamental Theory and Applications, 2003, 50(7): 945-953. Doi:10.1109/TCSI.2003.812606 |
| [7] |
刘海波, 吴德伟, 金伟, 等. Duffing振子微弱信号检测方法研究[J]. 物理学报, 2013, 62(5): 050501. |
| [8] |
王慧武, 丛超. 一种基于Duffing系统的信号检测与参数估计新方法[J]. 电子学报, 2016, 44(6): 1450-1457. Doi:10.3969/j.issn.0372-2112.2016.06.028 |
| [9] |
Liu C H, Zhou H S, Li X K. Detection method of a short-time double-Duffing chaotic oscillator array[C]//IEEE International Conference on Signal Processing, Communications and Computing. Xiamen, China: IEEE, 2017: 1-5.
|
| [10] |
Wu Y H, Zhu R G. Analysis of internal frequency's influence on blind detection of weak PSK signal by using duffing oscillator[C]//13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery. Guilin, China: IEEE, 2017: 2595-2605.
|
| [11] |
杨海博, 王海燕, 申晓红. 一种新的微弱未知信号混沌振子检测法[J]. 计算机应用研究, 2012, 29(3): 1073-1075. Doi:10.3969/j.issn.1001-3695.2012.03.075 |
| [12] |
Li N, Li X K, Liu C H. A detection method of Duffing oscillator based on adaptive adjusting parameter[C]//IEEE/OES China Ocean Acoustics Symposium. Harbin, China: IEEE, 2016: 1-5.
|
| [13] |
MIL-STD-188-141B. Interoperability and performance standards for medium and high frequency radio systems[S]. U.S: Department of Defense, 1999.
|
| [14] |
金虎, 王可人. 基于Duffing振子的直接序列扩频信号载波检测方法[J]. 电路与系统学报, 2009, 14(1): 23-27. Doi:10.3969/j.issn.1007-0249.2009.01.005 |
| [15] |
吴彦华, 马庆力. Duffing振子微弱信号盲检测方法[J]. 系统工程与电子技术, 2017, 39(11): 2414-2421. Doi:10.3969/j.issn.1001-506X.2017.11.04 |
| [16] |
王丽霞.混沌弱信号检测技术[D].哈尔滨: 哈尔滨工程大学, 2011.
|
| [17] |
李国正, 张波. 基于Duffing振子检测频率未知微弱信号的新方法[J]. 仪器仪表学报, 2017, 38(1): 181-189. Doi:10.3969/j.issn.0254-3087.2017.01.024 |
| [18] |
金虎. 基于Duffing振子的DSSS信号率线检测[J]. 电讯技术, 2011, 51(7): 42-46. Doi:10.3969/j.issn.1001-893x.2011.07.009 |
| [19] |
Liu Y L, Jiang Y Z, Jiang W, et al. Estimation algorithm of Doppler shift and time delay in HF channel sounding[C]//IEEE 10th International Conference on Electronic Measurement & Instruments. Chengdu, China: IEEE, 2011, 3: 350-354.
|
 2019, Vol. 36
2019, Vol. 36 


