2. 中国科学院大学, 北京 100049;
3. 海南省地球观测重点实验室, 海南 三亚 572029
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Earth Observation of Hainan Province, Sanya 572029, Hainan, China
电离层是地球大气层的重要圈层之一,探索电离层电子密度的空间分布状况对研究空间天气状况[1]、电离层震前异常[2]、赤道异常和威德尔海异常现象[3]等都具有重要意义。
电离层电子密度的可视化研究不仅可以让用户以直观的方式分析数据,而且有助于发现数据中所隐藏的复杂规律[4]。传统的电离层数据可视化主要有面绘制[5-7]、定制kml文件[8]等方法,但这些方法只表达出数据的部分信息特征,无法反映出原始数据场的全貌和细节。直接体绘制方法从原始三维数据出发,可以显示出三维数据场中各组成分量的空间分布状况,主要包括足迹表法、错切变形法、光线投射法和三维纹理映射法等主要算法[9]。这些体绘制方法已被广泛应用于空间电磁场、气象和地球科学领域,以促进可视化分析和科学研究,如三维磁层渲染[10]、飓风[11]和台风[12]模拟、大气温度可视化[13]、地震数据可视化[14-15],但很少用于电离层电子密度可视化。虽然基于球体八叉树的空间网格被用于电离层电子密度的三维体可视化,但在索引时间序列空间数据时存储各个八叉树需要大量空间,这给后端数据存储和网络数据传输造成了挑战;并且细节程度的提高会造成存储复杂度成几何级数的增加,即使硬件加速,可视化效率也很低[16-17]。基于光线投射的体绘制方法具有较好的可视化质量,现在可以实现基于虚拟地球电磁环境体数据的可视化[18],但尚未被用于电离层电子密度可视化,且其可视化程序无法在Web环境中实现。
为解决以上电离层电子密度可视化存在的问题,本文主要完成以下工作:
首先,为解决数据在Web上传输和实时可视化的问题,利用视频压缩编码方法,将电离层电子密度数据压缩为视频流,便于数据在网络中传输和实现不同时序数据的可视化;其次,为解决可视化质量差的问题,利用基于GPU加速的光线投射体绘制方法对大区域、多维、多时相的电离层电子密度进行可视化表达,并采用自适应步长采样以及早期光线终止法,提高绘制效率;最后,将电离层电子密度数据及丰富的地理背景集成在开源虚拟地球平台Cesium上,可以让更多专业人员和公众看到更高质量的电离层电子密度变化,并通过交互式查询和探索原始数据,分析隐藏的电离层变化规律和关系。
1 数据和预处理数据编码压缩是提高海量数据预处理能力的一个有效手段,主要有两方面的优点:一是降低内存需求,同时提高时域相关数据的交互性;二是可以减少这些数据的传输和处理时间,这对基于远程实现的可视化系统来说更为重要[19]。因此,有必要对原始电离层电子密度数据进行预处理,将数据压缩为视频流进行传输。下面详细介绍整个预处理过程。
1.1 数据来源及特点本文用到的电离层电子密度数据是由中国科学院国家空间科学中心提供的电离层电子密度同化数据。数据格式为NetCDF,数据经度范围为70°~140°,纬度范围为15°~55°,高度范围为100~920 km,时间跨度为4 h,经度和纬度间隔都为2°,高度间隔为20 km,时间间隔为1 h。
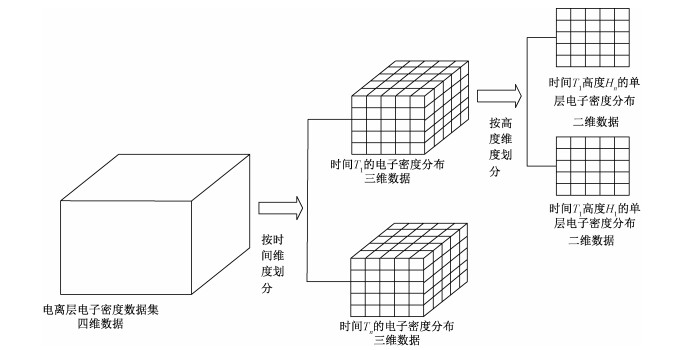
1.2 数据分解原始电离层电子密度数据具有经度、纬度、高度、时间四维特征,本文采用文献[20]中的算法将电离层电子密度数据先按照时间维度划分为一系列空间结构相一致的三维体数据,然后将每一时相的数据按高度分层,处理为一系列结构相一致的二维网格数据,如图 1所示,每个网格点包含某个空间位置的电子密度信息。
|
Download:
|
| 图 1 将四维电离层电子密度数据处理为一系列二维网格 Fig. 1 Split of the four-dimensional ionospheric electron density data into a series of two-dimensional grids | |
当原始电离层电子密度数据被处理为二维网格数据后,将数据从标量空间转换到RGB空间,以便后期将数据编码为视频。本文针对每一高度层中的网格,取每个网格4个顶点数据的平均值作为该网格的电子密度值。然后,将每个网格的电子密度值通过下式归一化到[0, 1]之间,以便于转换到RGB色彩空间:
| $ {D_{i,j}} = \left( {G{E_{i,j}} - G{E_{\min }}} \right)/\left( {G{E_{\max }} - G{E_{\min }}} \right), $ | (1) |
式中:GEi, j是每个网格所代表的电子密度值,GEmax和GEmin是整个电离层电子密度数据集的最大值和最小值,Di, j称为原始标量值。
将原始标量值Di, j乘以255后赋予RGB色彩空间的R色彩分量,G色彩分量和B色彩分量都赋予0,因此转换后的RGB色彩分量可以用下式表示:
| $ (R,G,B) = \left( {{D_{i,j}} \times 255,0,0} \right). $ | (2) |
借助MATLAB软件,设计程序将不同高度层的R、G、B色彩分量合成为RGB图像。图 2(a)~2(d)分别是色彩分量合成后不同高度层的RGB图像。最后,将不同高度层的RGB图像合成为一张代表某一时相电离层电子密度数据的大图像。

|
Download:
|
| 图 2 不同高度层的RGB图像 Fig. 2 RGB images of different height layers | |
当不同时相的电离层电子密度原始数据被处理为RGB图像后,利用视频编码方法将一系列RGB图像压缩为视频数据。视频文件的编码和解码时间受到多种因素的影响,其中,最大的影响因素是视频压缩编解码器和色度子采样模型。目前适用于Web环境的视频编解码器主要有H.264、VP8、VP9等,色度子采样模型主要有YUV4:4:4、YUV 4:2:0、YUV 4:2:2等[20]。综合考虑视频质量和解码效率两方面,本文选择的视频编解码器为VP9,色度子采样模型为YUV4:4:4。
2 基于GPU加速的电离层电子密度光线投射体绘制方法为实现高质量和高效率的可视化,本文基于WebGL可编程渲染管道,设计顶点着色程序和片段着色程序。
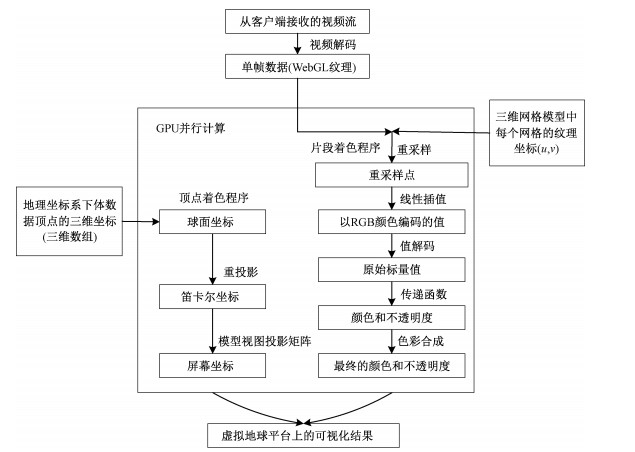
顶点着色程序针对电离层电子密度三维网格的每个顶点运行一次,主要负责完成一系列坐标转换工作,最终确定顶点在屏幕上的位置。片段着色程序针对每个屏幕像素运行一次,它主要负责计算顶点的纹理坐标,进行纹理重采样,解析相应的数据值,以及将数据值通过传递函数映射为相应的颜色和不透明度,然后经过一定的融合处理,把最终渲染结果显示在屏幕上。整体流程如图 3所示。
|
Download:
|
| 图 3 基于GPU加速的电离层电子密度光线投射体绘制 Fig. 3 GPU-accelerated ray-casting-based volume rendering algorithm of ionospheric electron density | |
在CPU中计算每个体素顶点在地理坐标系下的三维坐标,以三维数组的形式存储。在实时渲染中,因为GPU渲染管线不直接采用球面坐标,因此3D几何图元必须以笛卡尔坐标表示[11]。当地球被视为球体时,在顶点着色程序中,每个体素顶点的球面坐标被转换为原点位于地球中心的笛卡尔坐标,转换公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {x = r\cos \alpha \cos \beta }\\ {y = r\cos \alpha \sin \beta }\\ {z = r\sin \alpha } \end{array}} \right.. $ | (3) |
式中:α、β、r为球面坐标,x、y、z为笛卡尔坐标。
当每个体素顶点的球面坐标转换为笛卡尔坐标后,使用由Cesium提供的模型视图投影(MVP)矩阵实现从笛卡尔坐标到屏幕坐标的最终坐标转换。
在光线投射体绘制方法中,不能通过笛卡尔坐标系下的光线采样位置来获取体数据值,需要完成笛卡尔坐标到纹理坐标的转换,这项工作是由片段着色程序来完成[18]。假设数据的计算范围是A0(lat0, lon0, h0)至A1(lat1, lon1, h1),首先把顶点着色程序传递过来的笛卡尔坐标(x,y,z)转换为球面坐标(r, α, β),转换公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {r = \sqrt {{x^2} + {y^2} + {z^2}} }\\ {\alpha = \arcsin \frac{z}{r}}\\ {\beta = \arctan \frac{y}{x}} \end{array}} \right.. $ | (4) |
将球面坐标通过插值转换为纹理坐标的公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {u = \left( {\alpha - la{t_0}} \right)/\left( {la{t_1} - la{t_0}} \right)}\\ {v = \left( {\beta - lo{n_0}} \right)/\left( {lo{n_1} - lo{n_0}} \right)}\\ {w = \left( {r - {h_0}} \right)/\left( {{h_1} - {h_0}} \right)} \end{array}} \right.. $ | (5) |
只有当纹理坐标u,v和w的值在0~1之间时,该纹理坐标才会对体绘制效果产生作用。如果纹理坐标值超出该范围,则不对该处的体数据进行绘制,这样可以减少无效数据的绘制,提高数据绘制效率。
2.2 自适应步长采样本文在客户端界面中设计了电离层电子密度层数控制模块,用户可以根据自身需求自由调节要显示的层数。在重采样过程中,为了既保证渲染质量又提高渲染效率,根据最大和最小层之间的高度间隔自适应计算采样步长。当最大和最小层之间的高度间隔由小变大时,增加采样步长;反之,减小采样步长。自适应采样步长计算公式为
| $ {\rm{Step}} = {\rm{ FixedStep }} \times \left( {{H_{\max }} - {H_{\min }}} \right)/{H_0}, $ | (6) |
式中:FixedStep为两层数据之间的采样步长基数,Hmax和Hmin分别为要显示的体数据的最大高度和最小高度,H0为两层数据之间的高度间隔。
2.3 传递函数设计传递函数实质上是将标量值映射为相应的颜色值。为了在采样点处应用传递函数,应首先根据采样点的纹理坐标得到采样点处的标量值。在片段着色程序中,当采样点在第z层和z+1层纹理之间时,通过采样点的纹理坐标得到这两层相同纹理坐标处的颜色值c1和c2。然后将c1、c2通过值解码转换为公式(1)所表示的原始标量值D1、D2,对D1、D2在z和z+1层之间进行线性插值得到采样点处的原始标量值。
本文设计多个可以在客户端界面中由用户自由调节的一维传递函数,每个传递函数都有不同个数的函数分界点和颜色区间,将传递函数转化为一维纹理传入GPU的片段着色程序参与计算。在计算电离层电子密度数据值对应的颜色值时,首先计算出代表电离层电子密度的原始标量值所对应的纹理坐标,确定其在哪两个分界点之间,然后在两个分界点之间进行线性插值求得采样点的颜色值。
2.4 颜色和不透明度合成光线投射体绘制的图像合成算法主要有两种,分别是从前向后和从后向前进行图像合成[21]。本文采用第一种图像合成算法,合成公式为
| $ \left\{ {\begin{array}{*{20}{l}} {{C_m} = C \times \left( {1 - {A_{m - 1}}} \right) + {C_{m - 1}} \times {A_{m - 1}}}\\ {{A_m} = A \times \left( {1 - {A_{m - 1}}} \right) + {A_{m - 1}}} \end{array}} \right.. $ | (7) |
式中:C、A代表第m个采样点对应的颜色值和不透明度,Cm-1、Am-1代表前m-1个采样点累积的颜色值和不透明度,Cm、Am代表光线穿过第m个采样点后累积的颜色值和不透明度。
利用这种图像合成算法的优势是可以通过设定适当的不透明度阈值,例如当Am>0.98时提前终止采样计算,以提高绘制效率。
3 实验及结果分析为了对本文所述方法进行验证,基于开源虚拟地球平台Cesium,对多维多时相电离层电子密度数据的可视化效果和效率进行实验。实验利用HTML、CSS、JavaScript、GLSL等编程语言,在Sublime环境下进行开发。利用JavaScript实现基于光线投射的体绘制框架,借助GLSL来实现顶点和片段着色程序的核心算法。用于视频编码的程序为FFmpeg,其包含用于VP9视频编码的库libvpx-vp9。可视化硬件环境为CPU Intel Core i7-6700HQ 2.60 GHz,内存为16 GB,显卡为Nvidia GeForce GTX 960 M(4 GB)。系统运行所需的服务器为node.js,测试所用客户端为360、Chrome、Firefox等浏览器。
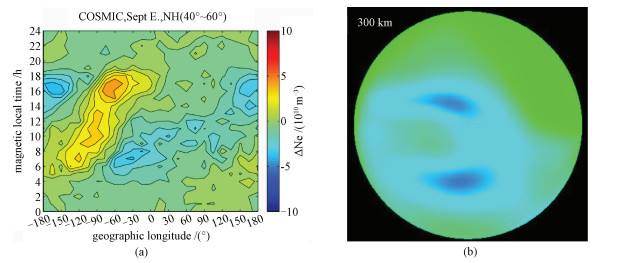
3.1 集成地理背景后的渲染质量分析与传统电离层电子密度可视化方法[7, 16](图 4(a)、4(b))相比,本文所述方法(图 5(a)~5(d))能形象直观地展示出电离层电子密度的空间分布状况,用户可以在客户端界面中自由选择需要显示哪一时相的数据以及数据层数,并且可以从多角度进行观察。此外,虚拟地球可以提供丰富的地理背景,在虚拟地球平台上添加天地图中文注记、天地图边界、以及地形等,借助地理背景,用户可以更好的分析理解电离层电子密度数据。图 5(a)和5(b)所使用的传递函数具有3个分界点,图 5(c)和5(d)所使用的传递函数具有6个分界点。
|
Download:
|
| 图 4 传统电离层电子密度可视化方法绘制结果 Fig. 4 Results of the traditional ionospheric electron density visualization rendering method | |

|
Download:
|
| 图 5 基于GPU加速的光线投射体绘制结果 Fig. 5 Results of GPU-accelerated ray-casting-based volume rendering algorithm | |
为验证视频流在数据传输效率上的优势,在局域网环境下,本文对基于视频编码方法得到的数据与网络环境中使用的其他空间压缩技术(基于有损压缩的JPEG图像编码/基于无损压缩的PNG图像编码)得到的数据进行了数据传输速度的对比实验,实验所用浏览器为360、Chrome和Firefox,实验结果如表 1所示。
|
|
表 1 数据传输速度比较 Table 1 Comparison of data transfer speed fps |
从表 1可以看出,在360、Chrome、Firefox浏览器中,基于视频编码的数据传输速度分别是JPEG和PNG编码方法的50和65倍、36和48倍、12和20倍。因此,将原始数据压缩为视频流进行传输可以明显提高数据传输效率。
3.3 渲染性能分析为验证提出的基于GPU加速的电离层电子密度光线投射体绘制方法的效率是否有所提高,本文进行了渲染性能验证测试,其方法主要是评估在各种约束条件下计算密集型可视化系统的每秒帧数(fps)[22]。
在图像合成过程中,在多个采样步长基数下,对分别应用自适应步长采样与固定步长采样算法后的体绘制速度进行对比,实验结果如表 2所示。
|
|
表 2 体绘制速度比较 Table 2 Comparison of volume rendering speed |
从表 2可以看出,在采样步长基数分别为100、300、500和1 000 m时,应用自适应步长采样算法后体绘制速度分别提高2.5%、3.3%、12.4%和39.9%。因此,自适应步长算法可以提高体绘制效率,而且在规定采样步长范围内,采样步长基数越大,体绘制效率提高越明显。
在图像合成过程中,当采用自适应步长采样时,对是否应用早期光线终止法的体绘制速度进行了对比,实验结果如表 3所示。
|
|
表 3 体绘制速度比较 Table 3 Comparison of volume rendering speed |
从表 3可以看出,在采样步长基数分别为100、300、500、1 000 m时,应用早期光线终止法后体绘制速度分别提高397.0%、124.1%、60.6%、10.4%。因此,在最终的图像合成过程中,当采用从前向后的图像合成算法时,应用早期光线终止法可以大幅度提高体绘制效率,而且在自适应采样步长基数较小时尤为明显。
4 结论本文从电离层电子密度的时空特征和实际需求出发,详细论述数据组织、视频压缩编码方法以及基于GPU加速的电离层电子密度光线投射体绘制方法。和已有的电离层电子密度可视化方法相比,本文所述方法解决了数据在Web上实时传输困难和可视化效果不佳的问题,实现了不同时相电离层电子密度的多层、动态、交互式可视化,在采样步长基数为100 m时,采用自适应步长采样和早期光线终止法体绘制效率提升近4倍。另外,基于开源虚拟地球平台Cesium,该方法可以轻松地集成到Web环境中,便于多用户共享。
在未来的研究中,可以将本文所述方法应用到其他的多维标量场中,比如大气温度、电离层离子温度等,以探究该方法的适用性。此外,将地学领域的空间分析方法和本文所述方法进行结合,使其不仅具有数据可视化功能,而且有助于空间分析和知识发现。
| [1] |
王小亚, 朱文耀. GPS监测电离层活动的方法和最新进展[J]. 天文学进展, 2003, 21(1): 33-40. Doi:10.3969/j.issn.1000-8349.2003.01.004 |
| [2] |
杨剑, 吴云, 周义炎. 基于电离层层析成像技术探测汶川地震前电离层异常[J]. 大地测量与地球动力学, 2011, 31(1): 9-14. |
| [3] |
马新欣, 林湛, 陈化然, 等. 基于COSMIC数据电离层电子密度空间分布变化[J]. 地球科学, 2017, 42(3): 479-484. |
| [4] |
Kehrer J, Hauser H. Visualization and visual analysis of multifaceted scientific data:a survey[J]. IEEE Transactions on Visualization & Computer Graphics, 2013, 19(3): 495-513. |
| [5] |
Watari S, Iwamoto I, Igarashi K, et al. 3-D visualization of the IRI model[J]. Advances in Space Research, 2003, 31(3): 781-783. Doi:10.1016/S0273-1177(03)00058-9 |
| [6] |
王鹏.基于HLA的空间环境要素建模与仿真技术研究[D].郑州: 解放军信息工程大学, 2006.
|
| [7] |
Wang H, Liu D, Zhang J. Vertical structure of longitudinal differences in electron densities at mid-latitudes[J]. Science Bulletin, 2016, 61(3): 252-262. Doi:10.1007/s11434-015-0993-7 |
| [8] |
Petry A, Pereira A G, Viero F, et al. Image generation and visualization system for ionosphere dynamics[C]//International Congress of the Brazilian Geophysical Society & Expogef, Rio De Janeiro, Brazil, 15-18 August. 2011: 2 150-2 153.
|
| [9] |
Kaufman A, Mueller K. The visualization handbook[M]. USA: Academic Press, 2005.
|
| [10] |
李大林, 李秀冰, 李英玉, 等. 基于体渲染技术的三维磁层可视化研究[J]. 微计算机信息, 2009, 25(9): 263-265. Doi:10.3969/j.issn.1008-0570.2009.09.110 |
| [11] |
Liang J, Gong J, Li W, et al. Visualizing 3D atmospheric data with spherical volume texture on virtual globes[J]. Computers & Geosciences, 2014, 68: 81-91. |
| [12] |
王伟, 周新春, 张国学. 面向灾害天气的三维动态仿真方法研究[J]. 人民长江, 2014, 45(2): 42-45. Doi:10.3969/j.issn.1001-4179.2014.02.013 |
| [13] |
Sarthou A, Mas S, Jacquin M, et al. Earthscape, a multi-purpose interactive 3d globe viewer for hybrid data visualization and analysis[C]//ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015, XL-3/W3: 487-493.
|
| [14] |
Patel D, Bruckner S, Viola I, et al. Seismic volume visualization for horizon extraction[C]//Proceedings of the IEEE Pacific Visualization Symposium. Taipei: IEEE, 2010: 73-80.
|
| [15] |
陈绍林, 张怀, 陈石, 等. 可扩展大屏幕高分辨率并行显示系统的构建及其在地学中的应用[J]. 中国科学院研究生院学报, 2009, 26(2): 243-250. |
| [16] |
He L M, Yang Y, Su C, et al. Grid-based representation and dynamic visualization of ionospheric tomography[C]//ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013: 71-76.
|
| [17] |
张宗佩.地月圈层立体网格理论与应用研究[D].郑州: 解放军信息工程大学, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D829535
|
| [18] |
杨超, 徐江斌, 吴玲达. 硬件加速的虚拟电磁环境体可视化[J]. 北京邮电大学学报, 2011, 34(1): 55-59. |
| [19] |
陈绍林, 张怀, 石耀霖. 地学中海量数据的并行可视化研究进展[J]. 中国科学院研究生院学报, 2008, 25(5): 577-584. |
| [20] |
Li W, Wang S. PolarGlobe:a web-wide virtual globe system for visualizing multidimensional, time-varying, big climate data[J]. International Journal of Geographical Information Science, 2017, 31(8): 1-21. |
| [21] |
叶良, 单桂华, 迟学斌.基于CUDA加速的光线投射法研究[C]//图像图形技术研究与应用学术会议论文集.北京: 北京交通大学出版社, 2010: 235-240.
|
| [22] |
Yang C, Wu H, Huang Q, et al. Using spatial principles to optimize distributed computing for enabling the physical science discoveries[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(14): 5498-5503. Doi:10.1073/pnas.0909315108 |
 2019, Vol. 36
2019, Vol. 36 


