2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
高精度厘定地物比辐射率(emissivity)是地表参数定量遥感反演中重要的研究方向之一。在大气透过率确定的情况下,热红外温度反演精度直接决定于比辐射率估计精度。Prata[1]研究指出,0.01的比辐射率误差将导致2 K的最终温度反演误差,Qin等[2]研究指出,0.01的比辐射率误差将导致最大约为1.6 ℃的最终温度反演误差。Wu和Smith[3]指出0.01的比辐射率误差会导致0.69 K的海表温度反演误差,Davies等[4]则指出在湖面温度反演中0.01的比辐射率改变会导致反演温度0.7~0.8 ℃的改变。在水体表面温度反演中,一般假设水体表面的成分、状态均一,比辐射率的空间分布基本一致,水体比辐射率统一采用定值。在大洋水体及绝大多数具有较低浓度悬浮泥沙、有机质、浮游动植物等水体中,比辐射率空间变化较小,基本符合这一假设。但在一些二类水体中,出现的蓝藻水华密集带和高浓度悬浮物极大改变了包括可见光、近红外和热红外的光谱特性,水体表面物理特性已经产生不可忽视的改变,而且空间差异显著。忽视水体表面蓝藻水华、悬浮泥沙的空间差异,采用与洁净水体相同的比辐射率,并必然对水体表面温度的定量反演造成很大的误差。
作为沿湖城市重要水源地的太湖,每年都受到蓝藻水华暴发的威胁,水体积温是预警蓝藻水华的重要因子,对水温的错误估计会对蓝藻水华预警产生不可忽视的影响。因此,高精度地定量反演水体表面温度,对于太湖水域的蓝藻水华预警有着重要意义。本文以太湖为研究区域,通过太湖水体组分样本的比辐射率实验室测量,建立基于蓝藻浓度和悬浮物浓度的比辐射率模型,开展MODIS通道31和通道32的比辐射率对水体组分浓度的响应规律研究;此外,进一步利用分裂窗算法(split window algorithm)对比比辐射率校正前后的太湖表面温度的变化,最后通过实测数据进行真实性检验。
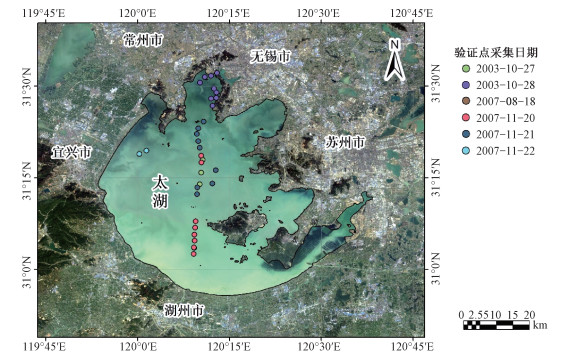
1 数据与实验方法 1.1 实验区概况太湖,横跨江、浙两省,地处长江三角洲南缘(图 1),界于30°55′40″~31°32′58″N,119°52′32″~120° 36′10″E之间,水面面积2 338 km2,流域面积36 895 km2,水深最大2.6 m,蓄水量44.30亿m3,为中国第3大淡水湖泊[5],承担向上海、无锡、苏州等大中城市供水的任务,兼具旅游、渔业、灌溉、航运等多种功能。太湖流域人口稠密、经济发达、是中国典型的城市化程度较高的区域之一,其人口、GDP以及财政收入分别达到全国的3%,10%和15%[6]。
|
Download:
|
| 图 1 太湖地理位置与验证点分布情况 Fig. 1 Location of Taihu Lake and the distribution of validation samples | |
有资料指出,20世纪80年代至21世纪初,太湖水环境质量持续下降[7],水体出现严重富营养化,蓝藻水华灾害频发。2007年5月,太湖爆发严重水华,致使无锡地区饮用水供应中断,被社会各界广泛关注。此外,太湖水体中的悬浮泥沙浓度较高,湖底淤积一定厚度的淤泥,沉积淤泥数量可达13.56亿m3。古河道内的淤泥厚度可达9 m左右,太湖内部的五里湖、梅梁湾等处淤泥厚度也达到0.8~1.5 m[8],加上太湖湖底平坦湖面开阔,非常利于形成风浪带动淤泥上扬再悬浮,并以湖心区、西部西南部沿岸淤泥上扬最为严重[9]。太湖水体组分浓度的时空变化幅度大、驱动因素复杂,以蓝藻为主的浮游藻类颗粒物浓度、悬浮颗粒物浓度峰值高、变化幅度大、时空分异规律显著,是太湖富营养化水体的典型特征。
水体温度对太湖水华灾害的形成具有显著驱动作用。太湖蓝藻每年都会在春季从底泥中苏醒、上浮、在水面生长、繁殖,然后在夏秋季形成水华,冬季则死亡分解、孢子下沉到底泥中过冬。每年春季,通常在西南太湖最早出现蓝藻水华密集带,并逐步向北扩散迁移,生物量急剧增大。春季积温对浮游藻类的生长繁殖有重要影响,春季回暖越早,高密度蓝藻水华密集带也出现得越早,也越容易出现蓝藻水华灾害[10]。因此,高精度反演、监测太湖水体温度,能够提高蓝藻水华灾害监测预警精度,具有重要的应用价值和现实意义。
1.2 数据介绍本论文涉及3部分数据:
1) 实验室测量数据
使用搭载PIKE Technologies红外积分球的傅里叶变换红外光谱仪Nicolet iS50(Thermo Fisher Scientific公司),分别测定湖水与不同浓度藻类、悬浮物样本的比辐射率,同一样本连续测定4~10次,计算平均值。
2) 遥感影像数据
MODIS数据:太湖地区2003年10月27日、28日,2004年4月28日、29日,2007年8月18日、20日,2007年11月20至22日9天的Terra星和Aqua星MODIS L1B数据共17景,反演蓝藻叶绿素a浓度、悬浮颗粒物浓度,并进行水体表面温度计算等。
Landsat数据:与MODIS数据的成像日期一致,用于对MODIS影像进行降尺度分析,反演更高空间分辨率的蓝藻叶绿素a浓度、悬浮物浓度,以完善比辐射率与蓝藻叶绿素a浓度、悬浮物浓度间的定量关系。
3) 外业测温数据
开展野外同步实验,采用接触式测量方法获取上层水体温度数据用于水体表面温度的真实性检验。与固定台站测量深度(一般在50~60 cm)不同,本实验的测量深度位于水面下1~10 cm处,温度数据通过连续3次测量取均值获得,为了保证测量数据的同步性,以卫星过境前后小于1 h为原则,从128个同步观测样点中最终筛选出32个样点用于验证,其位置分布如图 1所示。采样区域的水质状况之间差异较大,蓝藻方面有的样点处无蓝藻水华、有的覆盖有高密度蓝藻水华,悬浮物方面有的样点处浓度很高、有的较低,体现出明显的非均质现象。
1.3 大气校正方法遥感传感器接收到的反射辐射包含地物与大气两部分,在进行地物定量研究时,需消除大气辐射干扰。水体属于典型的弱反射地物,光谱信号很弱,以典型水体像元为例,传感器接收的辐射中,来自水体自身的不足20%,超过80%来自大气辐射[11]。因此,准确的大气校正方法对于高精度的水体组分定量遥感反演尤其重要。本研究中,通过同步部署太阳光度计CE-318获取卫星过境时的气溶胶光学厚度和水汽含量,并采用“6S”模型对遥感影像进行大气辐射校正。大气校正后在影像上分别随机选取典型的水体像元和植被像元,查看其光谱曲线,结果显示,大气校正后各像元光谱明显更接近标准光谱,大气校正效果良好。
1.4 比辐射率合成方法在光学的光谱分解理论中,仅包含一种地物的纯净像元称为端元,包含多种地物类型的称为混合像元。线性光谱模型假设,混合像元可由各端元光谱与其对应丰度组合而成,探测器接收到的是这些端元组分辐射强度线性相加的总表观辐射强度,假设在某个像元对应的瞬时视场中包含i种端元成分,则该像元的表达式可写为:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_\lambda } = \sum_{i = 1}^n {{a_i}} {\rho _{i\lambda }} + {\varepsilon _\lambda }, }\\ {\sum_{i = 1}^n {{a_i}} = 1, }\\ {0 < {a_i} < 1.} \end{array}} \right. $ | (1) |
式中:Rλ为像元在λ波段的反射率,ρiλ为端元i在λ波段的反射率,ai为端元i成分在该像元里的面积百分比,ελ是该像元在λ波段的残差。
类似地,假设地物混合像元的热红外波段比辐射率也符合线性分解模型,各端元成分彼此无影响并可以线性叠加。对于比辐射率线性合成模型中端元面积百分比,以水体成分的体积百分比(组分浓度)作为中间重要参数代入。
1.5 水体组分浓度反演方法太湖水体重要组分之中最明显的就是太湖蓝藻和悬浮泥沙浓度。叶绿素a浓度常作为浮游藻类生物量的表征指标,总悬浮物浓度常作为悬浮颗粒物含量的表征指标。叶绿素a在蓝波段的440 nm以及红波段的678 nm附近有显著吸收峰[12],在685~715 nm附近和550~570 nm附近有显著荧光峰,可作为叶绿素a的定量指标[13]。类似地,水体反射率随悬浮物含量的增加而增大,在500~650和780~830 nm两个区域内增幅最为明显,可以作为悬浮物浓度的定量指标[14-15]。本文使用祝令亚等[16-17]提出的方法:
| $ {C_{{\rm{chl}} - {\rm{a}}}} = 79.39 \times \left( {\frac{{{r_2}}}{{{r_1}}}} \right) - 16.09, $ | (2) |
| $ {C_{{\rm{ss}}}} = 101.85 \times \left( {\frac{{{r_4}}}{{{r_3}}}} \right) - 81.84. $ | (3) |
式中:Cchl-a为叶绿素a质量浓度,单位是μg/L;Css为悬浮物质量浓度,单位是mg/L;r1,r2,r3,r4分别为MODIS第1,2,3,4波段校正后的反射率。
针对式(2)、式(3)分别基于实测数据进行验证,结果显示:式(2)相关指数R2为0.81,均方根误差RMSE为13.48 μg/L;式(3)相关指数R2为0.85,均方根误差RMSE为5.93 mg/L。
1.6 温度反演方法目前遥感温度反演已形成较为完备的理论与应用体系,涵盖单窗算法、分裂窗算法、多角度/多实相/多通道算法3大类及其他特殊算法,其中以分裂窗算法最为成熟,应用最为广泛[18]。McMillin[19]最早提出分裂窗算法,在此基础上有很多学者进行改进,提出约20种算法[20],区别在于算法表现形式与参数估算方式[21]。覃志豪等[22]采用适用于NOAA/AVHRR数据的算法[2],提出面向MODIS数据的局地分裂窗温度反演模型,该算法仅利用大气透过率、地表比辐射率2个参数,就能够开展各种地物目标的热红外温度反演,计算简单,模型可靠,精度高,是比较常用的分裂窗算法之一[22-24]:
| $ {T_{\rm{S}}} = {A_0} + {A_1}{T_{31}} - {A_2}{T_{32}}, $ | (4) |
| $ {A_0} = \frac{{{D_{32}}\left( {1 - {C_{31}} - {D_{31}}} \right)}}{{{D_{32}}{C_{31}} - {D_{31}}{C_{32}}}}{a_{31}} - \frac{{{D_{31}}\left( {1 - {C_{32}} - {D_{32}}} \right)}}{{{D_{32}}{C_{31}} - {D_{31}}{C_{32}}}}{a_{32}}, $ | (5) |
| $ {A_1} = 1 + \frac{{{D_{31}}}}{{{D_{32}}{C_{31}} - {D_{31}}{C_{32}}}} + \frac{{{D_{32}}\left( {1 - {C_{31}} - {D_{31}}} \right)}}{{{D_{32}}{C_{31}} - {D_{31}}{C_{32}}}}{b_{31}}, $ | (6) |
| $ {A_2} = \frac{{{D_{31}}}}{{{D_{32}}{C_{31}} - {D_{31}}{C_{32}}}} + \frac{{{D_{31}}\left( {11 - {C_{32}} - {D_{32}}} \right)}}{{{D_{32}}{C_{31}} - {D_{31}}{C_{32}}}}{b_{32}}, $ | (7) |
| $ {C_i} = {\varepsilon _i}{\tau _i}(\theta ), $ | (8) |
| $ {D_i} = \left[ {1 - {\tau _i}(\theta )} \right]\left[ {1 + \left( {1 - {\varepsilon _i}} \right){\tau _i}(\theta )} \right]. $ | (9) |
式中:TS是地表温度;T31和T32是MODIS第31、32波段的亮度温度;τi(θ)是视角为θ的大气透过率;εi是波段i的水体比辐射率,取值ε31=0.996 83,ε32=0.992 324。对于温度反演的其他重要环节,如亮度温度计算、水汽含量反演、大气透过率计算、温度校正、角度校正等参考Gao等的工作成果[25]。
1.7 反演精度改善量评价相对于使用固定值比辐射率,基于水体组分浓度计算得到比辐射率并进行温度反演,其反演结果存在差异。为了描述精度提高的程度,本文构建温度反演改善指数(temperature retrieving improvement index):
| $ \Delta T = \left| {T - {T_0}} \right| - \left| {{T^\prime } - {T_0}} \right|. $ | (10) |
式中:T0为实测温度,T是基于传统比辐射率固定值反演的水体温度;T′为比辐射率校正函数计算的温度反演数值。|T-T0|与|T′-T0|分别为两种方法温度反演数据与实测温度数据的差值,用于对比比辐射率函数引入前后水体表面温度反演结果的误差大小,以评价比辐射率函数的引入对温度反演结果改善的贡献。若引入比辐射率函数使反演误差减小,则|T′-T0|小于|T-T0|,ΔT为正值,且ΔT越大代表温度反演改善越明显,最终反演精度越高。
2 结果与分析 2.1 比辐射率拟合实验测定含有不同叶绿素a浓度的蓝藻、悬浮物的混合水样的比辐射率曲线,进行不同蓝藻、悬浮物浓度与水体比辐射率的拟合。其中湖水、蓝藻、沉积物均采集自10月下旬的太湖北部梅梁湾湖区近岸处,采集时期处于夏秋季蓝藻旺盛生长期的末期,以大蓝藻生物量为特征。样本分为3大类:
1) 洁净湖水样本
洁净湖水样本,采自太湖上表层的洁净湖水。在采集时,选择水体清澈的取水点,容器内静置分离后取中段水体。洁净湖水样本数目:4个。采集地点位于太湖梅梁湾北部的4处不同地点。
2) 高浓度水华样本
水华样本,主要是采集漂浮于水体表面的高密度聚集的浮游藻类。旺盛生长的蓝藻会在水中上浮聚集,通过对蓝藻进行打捞,灌装高密度蓝藻水华富集液,并在实验室内按体积比例制取混合液,测定混合液比辐射率曲线。
3) 高浓度悬浮物样本
高浓度悬浮物样本,是采集太湖梅梁湾底部的表层软质底泥,按照基准体积比制取混合液,测定比辐射率曲线。
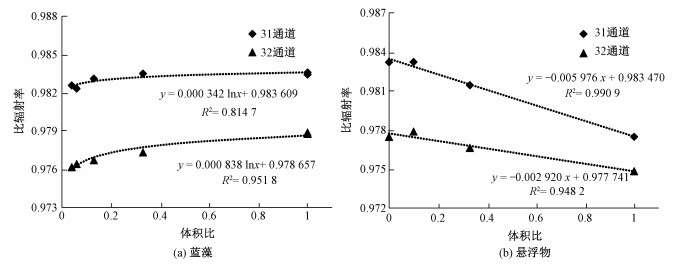
富集蓝藻基准样本和悬浮物基准样本用于模拟在自然环境下可能存在的蓝藻和悬浮物的最大浓度,将与实际观测到的蓝藻最大浓度和悬浮物最大浓度对应建立函数关系。实验所测得的比辐射率散点如图 2所示,其中,横轴为制取的水体组分体积比,纵轴为样本比辐射率值,图 2(a)、2(b)分别为比辐射率关于蓝藻和悬浮物体积比的散点图。
|
Download:
|
| 图 2 浓度组分与水体比辐射率的关系 Fig. 2 Relationships of emissivity with concentrations of water constituents | |
统计结果表明,蓝藻浓度与比辐射率关系拟合效果最好的是对数函数,决定系数R2在MODIS 31通道为0.81,在MODIS 32通道为0.95;悬浮物浓度与比辐射率关系拟合效果最好的为一次函数,决定系数R2在MODIS 31通道为0.99,在MODIS 32通道为0.95。
基于线性光谱分解模型,可以利用已知的端元丰度从总体比辐射率中分离出蓝藻(或悬浮物)基准样本的端元比辐射率值,再根据线性光谱混合模型,计算特定丰度下蓝藻基准样本、悬浮物基准样本和洁净湖水3种端元混合的比辐射率数值。根据实验室测量结果,太湖洁净湖水4个样本的比辐射率值基本一致,取其均值作为洁净湖水端元的发射率曲线和比辐射率值。最终得到湖水比辐射率与蓝藻、悬浮物的函数关系如表 1所示。其中考虑蓝藻或(与)悬浮物的3组公式基于仅考虑湖水的公式,需要注意的是,在仅考虑洁净湖水的情况下太湖水体比辐射率与第1.6小节中原始算法所使用的水体比辐射率不一致,有可能是受到水体中不同的有机物或无机盐离子的影响。
|
|
表 1 水体比辐射率与成分的函数关系 Table 1 Relationships of emissivity with water constituents concentrations |
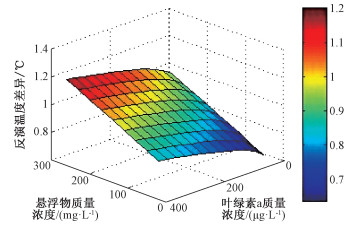
根据表 1中的公式,模拟多种浓度组合下的比辐射率及其温度反演情况,叶绿素a浓度从30~390 μg/L,以30 μg/L为步长、悬浮物浓度从30~270 mg/L,以30 mg/L为步长,分别计算不同样本的比辐射率变化,并计算比辐射率校正后的温度数值与常用的比辐射率[25]温度反演结果的差值如图 3所示。
|
Download:
|
| 图 3 比辐射率校正前后的温度反演差异 Fig. 3 Temperature retrieval difference before and after introduction of emissivity correction | |
模拟结果显示,随叶绿素a和悬浮物浓度升高,反演温度均升高,且随悬浮物浓度升高反演温度升高速度更快。在综合考虑两个水体组分因子的情况下,对温度反演的最大影响大致在1.21 ℃;在较低的悬浮物浓度时,最大叶绿素a浓度对温度反演的影响大致在0.86 ℃;在较低叶绿素a浓度时,最大悬浮物浓度对温度反演的影响大致在0.98 ℃。
2.3 比辐射率及温度响应空间分析除模拟分析外,我们还进行了基于遥感影像的空间分析。以2007年11月20日为例,依次讨论太湖的水体组分浓度、比辐射率空间差异及对其温度反演的影响。图 4为2007年11月20日的太湖地区Aqua星MODIS L1B影像经过大气校正后的真彩色显示。

|
Download:
|
| 图 4 2007年11月20日太湖影像 Fig. 4 Image of Taihu Lake on Nov. 20, 2007 | |
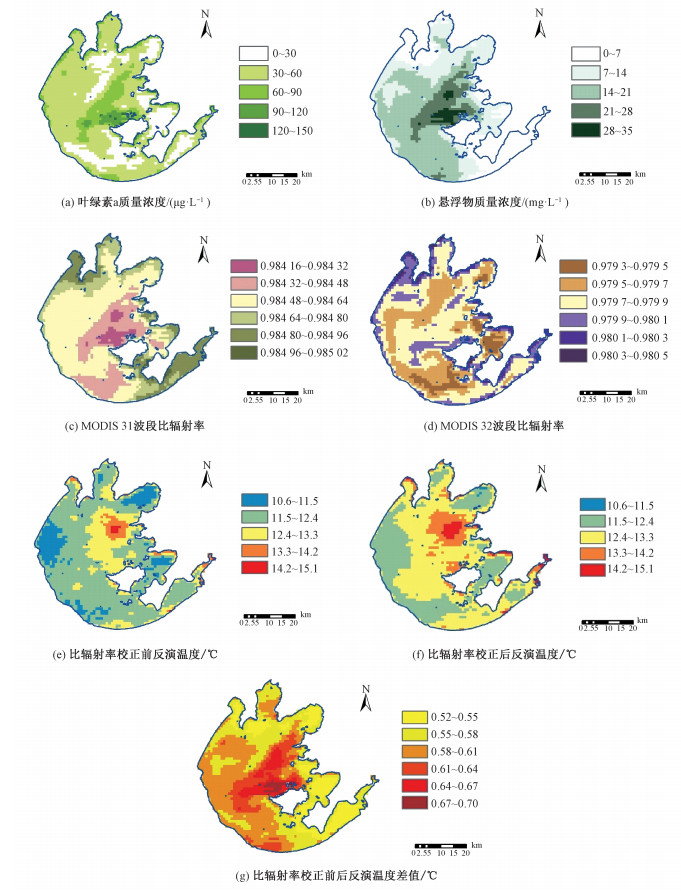
2007年11月20日当天太湖天气晴朗,湖面出现大面积蓝藻水华,卫星成像清晰,水面上空无云层遮挡。根据文中所述定量计算公式可计算得到叶绿素a浓度、悬浮物浓度、MODIS 31波段的校正比辐射率、MODIS 32波段的比辐射率及水体表面温度。同时,计算引入比辐射率校正函数前后的温度场,并对温度场的空间差异(图 5,表 2)进行分析。
|
Download:
|
| 图 5 水体组分浓度、比辐射率与水体表面温度的空间差异 Fig. 5 Concentrations of water constituents, emissivity, and comparison of the retrieving temperature | |
|
|
表 2 水体组分浓度、比辐射率、温度反演差异的统计表 Table 2 Statistics on water constituents concentrations, emissivity, and water surface temperature retrieved |
1) 水体组分空间分布
太湖水体组分中的浮游藻类、悬浮物空间分布受风浪影响明显,存在显著的空间差异性。2007年11月20日的浮游藻类主要分布在湖心区和北部的筑山湾、梅梁湾和贡湖湾区域;悬浮物浓度受风浪造成的湖心底泥再悬浮和入湖河流影响明显。叶绿素a浓度与悬浮物的最高浓度区域均出现在湖心区的西山岛西北方向附近,分别为148 μg/L与37 mg/L。高浓度分布区,沿东—西或东北—西南方向呈带状分布,二者呈现出较好的一致性。在太湖其他区域,叶绿素a浓度较为均匀,大多在30~60 μg/L之间;悬浮物浓度在西南太湖相对较高,在湖心以北的湾区与东太湖的悬浮物浓度相对较低。
2) 比辐射率空间分布
MODIS 31、32波段的比辐射率曲线符合正态分布,其变化区间均在0.001左右,其空间变化与叶绿素a、悬浮物浓度的空间分布具有良好的空间一致性,31、31波段的比辐射率最大值都出现在湖心区域。分析其空间分布的相似性,31波段的高比辐射率区域分布于东太湖及北部湖区,与高悬浮物浓度的空间分布基本吻合,在湖心区与高浓度叶绿素a、悬浮物的空间分布相似,在其他湖区受叶绿素a浓度影响更大;32波段比辐射率受叶绿素a浓度和悬浮物浓度影响相对较小,相对于31波段,32波段比辐射率与水体组分浓度的空间分布相似性较弱,除在湖心区与水体组分浓度的空间分布相似性稍大之外,在太湖南部沿岸区、东南部湖区及西北部沿岸区均有较高值出现。
3) 温度场空间差异
利用校正前后的比辐射率数据分别进行水体温度反演,获得太湖水体表面温度场。结果表明,校正前后的水体表面温度场空间分布特征稳定,表现出相似的空间分布规律,但水温数值大小发生一定的改变,与水体组分浓度有密切关系:最高温度出现在湖心区域以北,从最高温度区域向四周,水体表面温度逐步降低;最低温度位于西部和东北部湖区沿岸;引入不同水体组分浓度的比辐射率校正函数后,水体表面温度场整体上升约0.5~0.7 ℃,且引入比辐射率函数校正前后的水体温度场的差值出现显著的空间差异性,最大差异处位于湖心区域,西部沿岸带、西南沿岸带次之,其他湖区最小,这一空间分布规律与叶绿素a、悬浮物浓度空间分布基本吻合,且受悬浮物的空间分布情况影响更大。
2.4 真实性检验与效果评价以野外实测数据作为验证数据,对水体表面温度反演结果进行真实性检验,如图 6(a)所示。统计结果表明,对于全部32个验证点,反演误差的平均值为-0.40 ℃,反演误差绝对值平均为0.85 ℃,相对误差平均值为4%,反演误差的标准差为0.96 ℃,反演误差最大幅度为-2.13 ℃,66%的点的反演误差在1 ℃以内。相应地,对未经过比辐射率校正的原有算法的反演结果进行真实性检验,对于全部32个验证点,反演误差的平均值为-1.04 ℃,反演误差绝对值的平均值为1.26 ℃,相对反演误差的平均值为7%,反演误差的标准差为1.11 ℃,反演误差最大值为-3.56 ℃,50%的点的反演误差在1 ℃以内。

|
Download:
|
| 图 6 温度反演评价 Fig. 6 Temperature retrieval evaluation | |
反演温度-测量温度散点图只能反映算法整体的精度,无法反映算法中各子模块的精度,为了进一步研究比辐射率函数的引入对提高温度反演精度的贡献,由式(10)计算得到各验证点处温度反演的改善程度,如图 6(b)所示。
在全部32个验证点中,有28个点的反演误差减小,占比87.5%,有24个点的反演误差改善幅度在0.6 ℃左右或优于0.6 ℃,占样本数的62.5%。32个验证点的温度反演改善指数累加,得到∑ΔT=13.19 ℃,即比辐射率函数的引入整体显著改善了反演效果,提高了精度。
通过引入水体组分中叶绿素a浓度、悬浮物浓度,进行比辐射率校正,能够大幅度改善水体表面温度反演效果;真实性检验结果与实验测量值具有良好的一致性,证明基于水体组分浓度信息的比辐射率校正函数能够大幅度提高水体表面温度的遥感反演精度。同时,利用2007年11月20日的实测数据开展的真实性检验表明,水温反演精度有显著提高,变化幅度基本吻合数据模拟值。根据计算,相对于传统算法采用比辐射率值,考虑蓝藻和悬浮物浓度进行比辐射率校正的反演温度差异最大可达到1.21 ℃,但实际环境下,水体组分浓度普遍低于实验模拟数据,对于32个验证点,叶绿素a质量浓度最低为17 μg/L,悬浮物质量浓度最低为10 mg/L,叶绿素a质量浓度最高为89 μg/L,悬浮物质量浓度最高为63 mg/L,在水体组分浓度最大的验证点,比辐射率校正的水体表面温度的改善幅度也最为明显,达到0.78 ℃。较低的叶绿素a和悬浮物浓度,使得验证点的温度反演改善幅度受到限制,无法达到模拟实验中的改善程度。
3 总结展望在本文中,我们基于实验室测量数据提出水体比辐射率的拟合公式,在此基础上,先后进行温度反演与空间分析。实验和计算表明,蓝藻与悬浮物的存在对比辐射率及温度反演的确存在一定的影响:在本次实验条件下,只考虑浮游藻类比辐射率校正效果时,叶绿素a对温度反演的最大影响值约为0.86 ℃;只考虑悬浮物比辐射率校正效果时,悬浮物对温度反演的最大影响值约为0.98 ℃;在综合考虑浮游藻类和悬浮物的校正效果时,对温度反演影响的最大值达到1.21 ℃。引入基于水体组分的比辐射率校正函数能够有效校正水体表面温度的反演误差,在真实性检验中也证实了绝大多数验证点的水体表面温度的反演精度有较大改善。
在本文引入比辐射率校正函数前后温度反演结果的对比中,校正函数引入前的温度反演结果作为对照标准,所使用的比辐射率为原始算法本身提供,该比辐射率与实测的太湖洁净湖水比辐射率并不一致,使得在各组对比中蓝藻、悬浮物的存在及其对比辐射率值造成的改变不足以完全解释温度反演结果的差异。原始算法中水体比辐射率与实测洁净湖水的比辐射率差异是稳定的,并对温度反演结果存在较为明显的影响,在一些蓝藻、悬浮物浓度较低的情况下,该部分影响为引入校正函数前后温度反演差异的主要部分。这说明太湖的水体组分是复杂的,除蓝藻与悬浮物外太湖湖水中还存在其他影响水体比辐射率的组分,可能是水体中溶解性有机物或水中溶解的无机矿物质离子,尚需要进一步的探索。此外,本文所提出的比辐射率函数是否适用于其他二类水体,都有待后续工作的深入验证。
| [1] |
Prata A J. Land surface temperatures derived from the advanced very high resolution radiometer and the along-track scanning radiometer:1. Theory[J]. Journal of Geophysical Research Atmospheres, 1994, 99(D6): 13025-13058. Doi:10.1029/94JD00409 |
| [2] |
Qin Z, Dall'Olmo G, Karnieli A, et al. Derivation of split window algorithm and its sensitivity analysis for retrieving land surface temperature from NOAA-advanced very high resolution radiometer data[J]. Journal of Geophysical Research Atmospheres, 2001, 106(D19): 22655-22670. Doi:10.1029/2000JD900452 |
| [3] |
Wu X, Smith W L. Emissivity of rough sea surface for 8-13 μm:modeling and verification[J]. Applied Optics, 1997, 36(12): 2609-2619. Doi:10.1364/AO.36.002609 |
| [4] |
Davies J A, Robinson P J, Nunez M. Field determinations of surface emissivity and temperature for lake ontario[J]. Journal of Applied Meteorology, 2010, 10(4): 811-819. |
| [5] |
秦伯强, 胡维平, 陈伟民. 太湖水环境演化过程与机理[M]. 北京: 科学出版社, 2004.
|
| [6] |
秦伯强.太湖地区水资源和水环境面临的问题、原因与建议[C].中国水利学会.太湖高级论坛交流文集. 2004: 135-149.
|
| [7] |
秦伯强, 朱广伟, 杨宏伟, 等. 新方法、新理论为太湖环境治理和生态修复提供科技支撑[J]. 中国科学院院刊, 2017, 32(6): 654-660. |
| [8] |
袁旭音, 许乃政, 陶于祥, 等. 太湖底泥的空间分布和富营养化特征[J]. 华东地质, 2003(1): 20-28. |
| [9] |
胡开明, 王水, 逄勇. 太湖不同湖区底泥悬浮沉降规律研究及内源释放量估算[J]. 湖泊科学, 2014, 26(2): 191-199. |
| [10] |
孔繁翔, 马荣华, 高俊峰, 等. 太湖蓝藻水华的预防、预测和预警的理论与实践[J]. 湖泊科学, 2009, 21(3): 314-328. Doi:10.3321/j.issn:1003-5427.2009.03.002 |
| [11] |
王得玉, 冯学智, 马荣华. 太湖二类水体水色遥感的大气校正问题探讨[J]. 南京邮电大学学报(自然科学版), 2012, 32(2): 13-18. Doi:10.3969/j.issn.1673-5439.2012.02.003 |
| [12] |
Brivio P A, Giardino C, Zilioli E. Determination of chlorophyll concentration changes in Lake Garda using an image-based radiative transfer code for Landsat TM images[J]. International Journal of Remote Sensing, 2001, 22(2/3): 487-502. |
| [13] |
周艺, 周伟奇, 王世新, 等. 遥感技术在内陆水体水质监测中的应用[J]. 水科学进展, 2004, 15(3): 312-317. Doi:10.3321/j.issn:1001-6791.2004.03.009 |
| [14] |
俞宏, 蔡启铭, 吴敬禄. 太湖水体吸收系数与散射系数的特征研究[J]. 水科学进展, 2003, 14(1): 46-49. Doi:10.3321/j.issn:1001-6791.2003.01.008 |
| [15] |
马荣华, 戴锦芳. 结合Landsat ETM与实测光谱估测太湖叶绿素及悬浮物含量[J]. 湖泊科学, 2005, 17(2): 97-103. Doi:10.3321/j.issn:1003-5427.2005.02.001 |
| [16] |
祝令亚, 王世新, 周艺, 等. 应用MODIS监测太湖水体叶绿素a浓度的研究[J]. 遥感信息, 2006(2): 25-28. Doi:10.3969/j.issn.1000-3177.2006.02.008 |
| [17] |
祝令亚, 王世新, 周艺, 等. 应用MODIS影像估测太湖水体悬浮物浓度[J]. 水科学进展, 2007, 18(3): 444-450. Doi:10.3321/j.issn:1001-6791.2007.03.022 |
| [18] |
覃志豪, Arnon Karnieli. 用NOAA-AVHRR热通道数据演算地表温度的劈窗算法[J]. 国土资源遥感, 2001(2): 33-42. Doi:10.3969/j.issn.1001-070X.2001.02.007 |
| [19] |
McMillin L M. Estimation of sea surface temperatures from two infrared window measurements with different absorption[J]. Journal of Geophysical Research, 1975, 80(36): 5113-5117. Doi:10.1029/JC080i036p05113 |
| [20] |
王祥.基于国产自主卫星的海表温度红外遥感机理与算法研究[D].辽宁大连: 大连海事大学, 2013.
|
| [21] |
魏寒艳.基于MODIS数据的海表温度反演研究[D].合肥: 中国科学技术大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10358-1017192988.htm
|
| [22] |
覃志豪, 高懋芳, 秦晓敏, 等. 农业旱灾监测中的地表温度遥感反演方法:以MODIS数据为例[J]. 自然灾害学报, 2005, 14(4): 64-71. Doi:10.3969/j.issn.1004-4574.2005.04.011 |
| [23] |
买佳阳, 蒋雪中. 2000年以来长江河口海表温度变化MODIS分析[J]. 遥感学报, 2015, 19(5): 818-826. |
| [24] |
郭甜甜, 陈圣波, 陆天启. 基于MODIS数据的多时相海表温度反演:以海南岛西南部近海海域为例[J]. 热带海洋学报, 2017, 36(1): 9-14. |
| [25] |
Gao M, Qin Z, Xu B. Estimation of the basic parameters for deriving surface temperature from MODIS data[J]. Arid Zone Research, 2007, 24(1): 113-119. |
 2019, Vol. 36
2019, Vol. 36 


