2. 西班牙光子科学研究所, 卡斯特利德费尔斯 08860
2. ICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, Castelldefels 08860, Spain
在一维量子多体系统中,量子相变点附近的临界行为可以由纠缠熵关于系统尺寸或关于矩阵乘积态中截断维数的标度理论来刻画。基于(1+1)维共形场论,刻画一维量子临界性的纠缠熵标度理论已经被相对完整地建立起来[1-11],但是在二维量子多体系统中,由于(2+1)维共形场的不稳定性,无法直接将现有的一维标度理论直接推广到二维量子系统。目前常用于刻画二维量子系统临界性的方法,例如,寻找基态长程关联或分析低温下的热力学性质,从数值计算角度来讲都对计算精度和计算复杂度提出了很高的要求。并且相对于一维而言,如何通过纠缠熵关于二维量子系统中投影纠缠对态截断维数的标度行为来刻画二维量子系统的临界性目前还不完全清楚[12]。因此,有必要发展二维量子临界系统的标度理论。
最近,针对一维无穷长链上的平移不变量子系统中的基态问题所提出的时间矩阵乘积态,可以有效地反映系统基态的物理性质,特别是刻画临界系统中关联长度发散和纠缠熵发散的行为,以及给出临界系统的中心荷。时间矩阵乘积态被定义在二维张量网络中的实(虚)时间演化方向,它是一维的连续矩阵乘积态[13]。发展关于时间矩阵乘积态的纠缠熵标度理论对刻画临界系统的性质十分有帮助。
在这个工作中,我们利用数值重整化群方法,将时间矩阵乘积态推广到二维量子系统,并用于刻画二维量子系统在量子相变点附近的临界性。无论所描述的系统是一维还是二维量子系统,时间矩阵乘积态始终是一维量子态,因此可以通过时间矩阵乘积态结合一维量子临界系统的纠缠熵标度理论描述高维量子临界系统的性质。我们还建立了时间矩阵乘积态所刻画的临界系统纠缠熵和动力学关联长度与空间方向的矩阵乘积态所描述的纠缠熵和空间关联长度之间的等价性。
我们分别在蜂窝状六角格子和kagome格子上的自旋1/2海森堡反铁磁模型中利用时间矩阵乘积态研究临界点附近的标度行为,发现二维量子临界系统中的时间矩阵乘积态反映出与一维量子临界系统中的矩阵乘积态类似的纠缠熵对数发散型标度律。
1 从数值重整化群流到时间矩阵乘积态我们将提供一种基于数值重整化群的方法,建立起二维量子系统的基态纠缠熵与时间矩阵乘积态的纠缠熵之间的等价性。
首先,对数值重整化群做一个简单的回顾。尽管在二维或高维系统中不存在重整化流,但是在数值重整化群中通常人为地选择一条特殊路径来定义重整化流。这种做法相当于将一个二维或高维有限尺寸格点系统上的模型映射成一维有限长链上的等效模型,相应的代价是原模型中的部分最近邻相互作用在等效模型中被当作长程相互作用处理。由于该一维等效模型的存在,同样的方法可用于任意维度有限尺寸量子模型的讨论上。
考虑包含N个自旋的系统,其哈密顿量可一般性地表示为
| $ \hat H = \sum\limits_n {{{\hat h}^{\left[ {n,n + r} \right]}}} , $ | (1) |
式中ĥ[n, n+r]是间距为r的两体哈密顿量。通常,我们对一个随机初始化的矩阵乘积态采用虚时演化,以达到极小化能量、获得变分基态的目的。虚时演化过程可表示为
| $ \min \left\langle {\psi \left| {\hat H} \right|\psi } \right\rangle \rightleftharpoons \mathop {\lim }\limits_{\beta \to \infty } \left\langle {\psi \left| {{{\text{e}}^{ - \beta \hat H}}} \right|\psi } \right\rangle , $ | (2) |
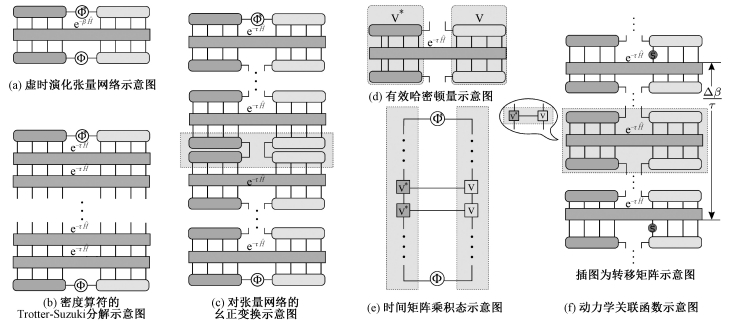
式中β=1/T, T为温度。虚时演化的图形表示如图 1(a)所示。利用数值重整化群流,系统的基态|ψ〉可表示为
| $ \left| \psi \right\rangle = \sum\limits_{{a_n},{b_n}} {{\Phi _{{a_n}{b_n}}}} \left| {\psi _{{a_n}}^L} \right\rangle \otimes \left| {\psi _{{b_n}}^R} \right\rangle , $ | (3) |
|
Download:
|
| 图 1 虚时演化和时间矩阵乘积态的示意图 Fig. 1 Diagrams of the imaginary time evolution and the time matrix product state | |
式中:{|ψanL〉}和{|ψbnR〉}分别表示从第n和第n+1格点之间对一维系统进行二分后获得的左侧和右侧半链上的一组正交归一基矢,其正交归一化条件为
| $ \left\langle {\psi _{{{a'}_n}}^L\left| {\psi _{{a_n}}^L} \right.} \right\rangle = {I_{{{a'}_n}{a_n}}}, $ | (4) |
| $ \left\langle {\psi _{{{b'}_n}}^R\left| {\psi _{{b_n}}^R} \right.} \right\rangle = {I_{{{b'}_n}{b_n}}}. $ | (5) |
方程(3)实际上是对任意多体量子纠缠态进行施密特分解,而将系统二分后左右两条半链之间的纠缠谱则被包含在Φ中。通过纠缠谱可计算出系统的纠缠熵。用方程(3)中的基态表示重写虚时演化过程,形式如下
| $ \begin{array}{l} \left\langle {\psi \left| {{{\rm{e}}^{ - \beta \hat H}}} \right|\psi } \right\rangle = \sum\limits_{\begin{array}{*{20}{c}} {a_n^{\left[ 0 \right]},a_n^{\left[ {N + 1} \right]}}\\ {b_n^{\left[ 0 \right]},b_n^{\left[ {N + 1} \right]}} \end{array}} {{\Phi _{a_n^{\left[ 0 \right]},b_n^{\left[ 0 \right]}}}\Phi _{a_n^{\left[ {N + 1} \right]},b_n^{\left[ {N + 1} \right]}}^ * } \cdot \\ \left\langle {\psi _{a_n^{\left[ 0 \right]}}^L\left| \otimes \right.\left\langle {\psi _{b_n^{\left[ 0 \right]}}^R\left| {{{\rm{e}}^{ - N\tau \hat H}}} \right|\psi _{a_n^{\left[ {N + 1} \right]}}^L} \right\rangle \otimes \left| {\psi _{b_n^{\left[ {N + 1} \right]}}^R} \right.} \right\rangle , \end{array} $ | (6) |
式中:τ是Trotter-Suzuki分解[14-16]的步长,N是一个极大的正整数,需保证β=Nτ足够大,方能达到模拟系统基态的目的。重写后的虚时演化过程如图 1(b)所示。如果在第j层Trotter-Suzuki切片之间插入幺正变换
| $ \begin{array}{*{20}{c}} {H_{a_n^{\left[ {j - 1} \right]}b_n^{\left[ {j - 1} \right]},a_n^{\left[ j \right]}b_n^{\left[ j \right]}}^{{\rm{eff}}} = \left\langle {\psi _{a_n^{\left[ {j - 1} \right]}}^L\left| \otimes \right.\left\langle {\psi _{b_n^{\left[ {j - 1} \right]}}^R\left| {{{\rm{e}}^{ - \tau \hat H}}} \right|\psi _{a_n^{\left[ j \right]}}^L} \right\rangle } \right.}\\ {\left. { \otimes \left| {\psi _{b_n^{\left[ j \right]}}^R} \right.} \right\rangle ,} \end{array} $ | (7) |
| $ H_{a_n^{\left[ {j - 1} \right]}b_n^{\left[ {j - 1} \right]},a_n^{\left[ j \right]}b_n^{\left[ j \right]}}^{{\rm{eff}}} = \sum\limits_{c_n^{\left[ {j - 1} \right]}} {{V_{c_n^{\left[ {j - 1} \right]},a_n^{\left[ {j - 1} \right]}a_n^{\left[ j \right]}}}V_{c_n^{\left[ {j - 1} \right]},b_n^{\left[ {j - 1} \right]}b_n^{\left[ j \right]}}^ * } . $ | (8) |
在此定义下,图 1(b)中的结构可表示为一系列有效哈密顿量的连乘。若对全部有效哈密顿量进行如方程(8)中的分解,那么将出现沿垂直于实空间方向(虚时间方向)延伸的两列新的矩阵乘积态,即时间矩阵乘积态,其表达式为
| $ \begin{array}{l} \left| {\psi _{a_0^{\left[ 0 \right]}a_n^{\left[ {N + 1} \right]}}^T} \right\rangle = \sum\limits_{\begin{array}{*{20}{c}} {c_n^{\left[ 0 \right]}, \cdots ,c_n^{\left[ N \right]}}\\ {a_n^{\left[ 0 \right]}, \cdots ,a_n^{\left[ N \right]}} \end{array}} {{V_{c_n^{\left[ 0 \right]}, \cdots ,a_n^{\left[ 0 \right]}a_n^{\left[ 1 \right]}}} \cdots {V_{c_n^{\left[ N \right]}, \cdots ,a_n^{\left[ N \right]}a_n^{\left[ {N + 1} \right]}}}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\left| {c_n^{\left[ 0 \right]}, \cdots ,c_n^{\left[ N \right]}} \right\rangle \otimes \left| {a_n^{\left[ 0 \right]}, \cdots ,a_n^{\left[ {N + 1} \right]}} \right\rangle , \end{array} $ | (9) |
| $ \begin{array}{l} \left| {\phi _{b_0^{\left[ 0 \right]}b_n^{\left[ {N + 1} \right]}}^T} \right\rangle = \sum\limits_{\begin{array}{*{20}{c}} {c_n^{\left[ 0 \right]}, \cdots ,c_n^{\left[ N \right]}}\\ {b_n^{\left[ 0 \right]}, \cdots ,b_n^{\left[ N \right]}} \end{array}} {{V_{c_n^{\left[ 0 \right]}, \cdots ,b_n^{\left[ 0 \right]}b_n^{\left[ 1 \right]}}} \cdots {V_{c_n^{\left[ N \right]}, \cdots ,b_n^{\left[ N \right]}b_n^{\left[ {N + 1} \right]}}}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\left| {c_n^{\left[ 0 \right]}, \cdots ,c_n^{\left[ N \right]}} \right\rangle \otimes \left| {b_n^{\left[ 0 \right]}, \cdots ,b_n^{\left[ {N + 1} \right]}} \right\rangle . \end{array} $ | (10) |
在时间矩阵乘积态中,指标{cn}的作用相当于空间矩阵乘积态中的物理指标,而{an}和{bn}的作用相当于辅助指标。因此可以发现,方程(7)中所定义的有效哈密顿量实则为时间矩阵乘积态内积的转移矩阵。在时间矩阵乘积态的框架下,可以将方程(6)中的虚时演化过程重新表述为
| $ \begin{array}{l} \left\langle {\psi \left| {{{\rm{e}}^{ - \beta \hat H}}} \right|\psi } \right\rangle = \sum\limits_{\begin{array}{*{20}{c}} {a_n^{\left[ 0 \right]},a_n^{\left[ {N + 1} \right]}}\\ {b_n^{\left[ 0 \right]},b_n^{\left[ {N + 1} \right]}} \end{array}} {{\Phi _{a_n^{\left[ 0 \right]},b_n^{\left[ 0 \right]}}}\Phi _{a_n^{\left[ {N + 1} \right]},b_n^{\left[ {N + 1} \right]}}^ * } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\langle {\phi _{b_0^{\left[ 0 \right]}b_n^{\left[ {N + 1} \right]}}^T\left| {\psi _{a_0^{\left[ 0 \right]}a_n^{\left[ {N + 1} \right]}}^T} \right.} \right\rangle . \end{array} $ | (11) |
该式等号成立的条件是Φ为式(7)中有效哈密顿量的最大本征态。
2 时间矩阵乘积态的纠缠熵与关联长度由于时间矩阵乘积态是一维的平移不变矩阵乘积态,因此可以很方便地求出纠缠熵和关联长度,并且建立在一维矩阵乘积态基础上的纠缠熵标度理论对时间矩阵乘积态同样有效。由于时间矩阵乘积态的纠缠熵和关联长度分别等价于量子系统的基态纠缠熵和动力学关联长度,这为研究二维量子临界系统提供了便利。
由于时间矩阵乘积态沿实(虚)时间方向具有平移不变性,因此在系统基态无简并的情况下,有动力学关联长度ξT=1/(lnλ0-lnλ1),其中λ0和λ1是方程(7)中有效哈密顿量的最大和次大本征值。也就是说有效哈密顿量的能隙给出基态的动力学关联长度。对于纠缠熵,我们要求时间矩阵乘积态沿实(虚)时间方向满足中心正则条件,满足条件的时间矩阵乘积态的规范变换由Φ决定。由于有效哈密顿量具有厄米性,时间矩阵乘积态的纠缠谱实际上就是Φ的奇异值谱,即
需要说明的是,一方面上述等价性建立在数值重整化群流能够在多大程度上反映真实的二维量子多体系统的基态;另一方面,方程(8)中分解的对称性也制约着二者的等价性。我们通过数值模拟发现,即使这两方面要求并不能够严格地满足,时间矩阵乘积态依然能够反映出基态关联长度和纠缠熵的特性。
3 结果和讨论首先,在蜂窝状六角格子上的自旋1/2各向异性海森堡反铁磁模型中,应用时间矩阵乘积态研究基态临界行为。系统的哈密顿量为
| $ \hat H = J\sum\limits_{ < ij > } {{{\hat S}_i}} {{\hat S}_j} + J'\sum\limits_{ < lm > } {{{\hat S}_l}} {{\hat S}_m}, $ | (12) |
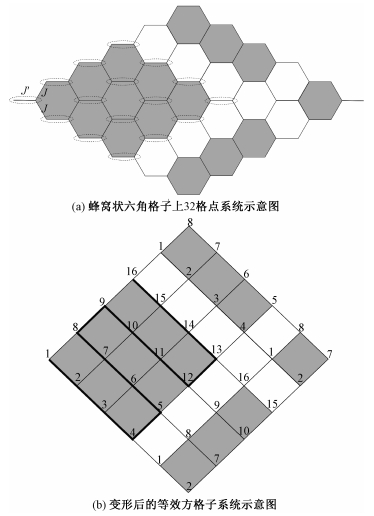
式中:J和J′分别是沿着如图 2(a)所示的不同方向的耦合系数。在反铁磁相互作用情况下,哈密顿量中的耦合系数大于零。在热力学极限下,模型的临界点位于Jc=0.5(4)[17]。在临界点左侧(J/J′<Jc)时,系统的基态处于有能隙的二聚体相,而在临界点的右侧(J/J′≥Jc)时,系统的基态处于无能隙的奈耳相[17]。为方便起见,令J′=1作为能标。
|
Download:
|
| 图 2 有限尺寸格点系统示意图 Fig. 2 Diagrams of the finite size system | |
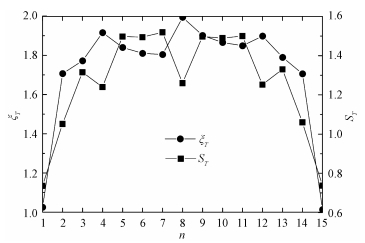
利用密度矩阵重整化群方法研究该模型的基态性质,取有限尺寸的蜂窝状六角格子,如图 2(a)所示,每个自旋占据格子中的一个交点,自旋与自旋之间的相互作用由黑色实线表示。图中阴影部分为选取的有限尺寸格子,相邻阴影部分之间的黑色实线代表边界相互作用。在后面的计算中,考虑两个方向的周期边界条件。为便于程序设计,将图 1(a)中虚线圆圈中的两个自旋用一个等效的格点代替,因此蜂窝状六角格子等效为一个方格子,如图 2(b)所示,每个等效格点在矩阵乘积态中用一个张量表示,矩阵乘积态以图中序号所表示的路径,遍历方格子中的所有格点。因此很容易发现,某些最近邻相互作用在矩阵乘积态中以长程相互作用的形式出现。由于矩阵乘积态中不包含格点的平移不变性,因此应在每个格点处观测时间矩阵乘积态的纠缠熵ST与关联长度ξT。ST和ξT与空间位置的关系如图 3所示。为尽量减小边界的影响,选择远离边界的格点计算ST与ξT,并对被选中的格点取平均值。
|
Download:
|
| 图 3 时间矩阵乘积态的纠缠熵ST和动力学关联长度ξT随观测位置的变化趋势图 Fig. 3 The position dependences of entanglement entropy ST and dynamic correlation length ξT | |
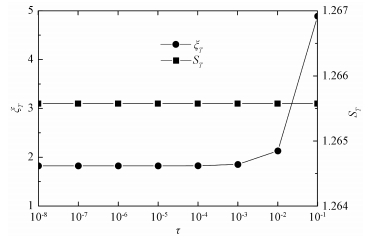
为排除Trotter-Suzuki分解的误差对结果的影响,令步长τ逐渐减小并趋于零,以观察纠缠熵和关联长度关于步长τ的收敛情况。尽管Trotter-Suzuki误差不能被完全避免,但是如图 4所示,我们发现纠缠熵ST和动力学关联长度ξT在τ<10-4以后几乎达到饱和值,因此在后面的计算中固定取值为τ=10-6,以平衡Trotter-Suziki误差与机器精度之间的关系。
|
Download:
|
| 图 4 ST和ξT关于Trotter-Suzuki步长的收敛趋势示意图 Fig. 4 Trotter-Suzuki step dependencs of ST and ξT | |
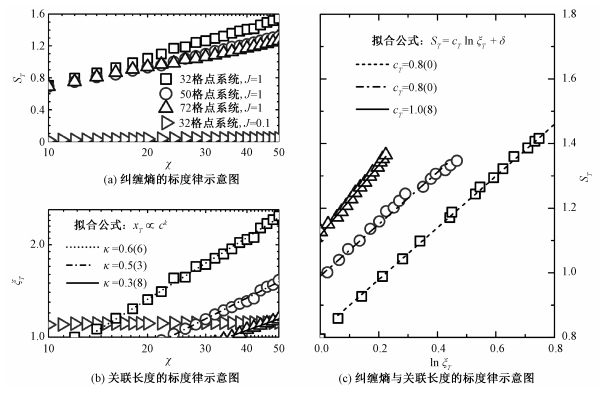
通过调节耦合系数J的大小,蜂窝状六角格子上的自旋1/2各向异性海森堡反铁磁模型会经历两个不同的相区,分别是从基态到第一激发态之间存在激发能隙的二聚体相以及无激发能隙奈尔相[17]。如图 5(a)所示,在两个不同的相区内,纠缠熵ST和关联长度ξT关于时间矩阵乘积态的截断维数χ存在不同类型的标度关系。当J=0.1时,系统处于二聚体相,纠缠熵和关联长度随着截断维数的增加都快速收敛到有限大小的饱和值。由于时间矩阵乘积态实质上是一维矩阵乘积态,并且已知对于固定截断维数的时间矩阵乘积态,有限大小的截断维数将限制系统的关联长度[7]。对于基态有激发能隙的系统,基态关联函数呈指数衰减,也就是说基态只存在短程关联,关联长度接近晶格常数。因此随着截断维数的增加,系统关联长度会出现短暂的上升,当关联长度上升至接近晶格常数(饱和值)时,即使继续增加截断维数也不会再观察到关联长度的上升。而受到关联长度的限制,纠缠熵同样随着截断维数的增加而短暂上升,当关联长度达到饱和值的同时,纠缠熵也收敛到一个有限大小的饱和值。
|
Download:
|
| 图 5 蜂窝状六角格子上自旋1/2海森堡反铁磁体的纠缠熵ST和关联长度ξT标度律示意图 Fig. 5 The scaling laws of the entanglement entropy ST and the correlation length ξT | |
在各向同性点J=1处,系统处于奈尔相中,纠缠熵在出现有限尺寸效应以前,随着截断维数的增加呈对数型发散,关联长度与截断维数之间呈指数型发散,具体表示为
| $ {S_T} = \alpha \ln \chi + {\rm{const}},{\xi _T} \propto {\chi ^\kappa }. $ | (13) |
上述行为与一维临界系统中的纠缠熵和关联长度关于截断维数的标度行为一致。我们在不同的尺寸下观察临界系统纠缠熵和关联长度的标度关系,二者满足
| $ {S_T} = {c_T}\ln {\xi _T} + {\rm{const}}. $ | (14) |
其中,因子cT=α/κ类似于一维量子临界系统的中心荷,随着系统尺寸的增加,有cT~1。
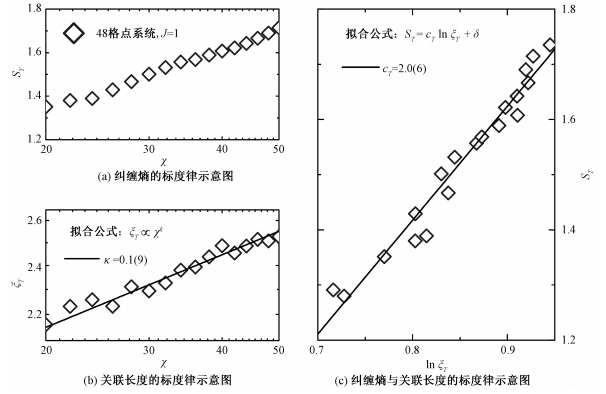
我们还在kagome格子上的自旋1/2各向同性海森堡反铁磁模型中,利用时间矩阵乘积态的纠缠熵标度行为研究系统的基态。如图 6所示,时间矩阵乘积态的纠缠熵和关联长度清晰地反映出系统基态的临界行为。我们的结果与支持kagome格子上的自旋1/2各向同性海森堡模型中的基态是无激发能隙的量子自旋液体这一结论的实验和理论预言[18-30]相一致。
|
Download:
|
| 图 6 kagome格子上自旋1/2海森堡反铁磁体的基态纠缠熵ST和关联长度ξT关于标度律示意图 Fig. 6 The scaling laws of the entanglement entropy ST and the correlation length ξT for the spin-1/2 HAFM on the kagome lattice | |
本文提出一种用于刻画二维量子临界系统的一维量子态——时间矩阵乘积态。时间矩阵乘积态的纠缠熵和关联长度与二维量子系统中通过数值重整化群流所定义的纠缠熵和动力学关联长度是等价的。在蜂窝状六角格子上的自旋1/2各向异性海森堡反铁磁模型中展示了时间矩阵乘积态所给出的纠缠熵和关联长度在2个相区内的不同标度行为,在有能隙的二聚体相中纠缠熵和关联长度关于增加的截断维数先短暂上升后快速收敛,而在无能隙的奈尔相中纠缠熵关于增加的截断维数呈对数型发散,关联长度呈指数型发散。还通过kagome格子上自旋1/2各向同性海森堡模型对应的时间矩阵乘积态的纠缠熵标度行为,发现纠缠熵关于截断维数的变化满足临界系统的纠缠熵标度律。本文提出的方法很好地给出了有能隙的二聚体相与无能隙的奈尔相内的纠缠熵标度行为,但是在靠近相边界的区域,由于计算误差的影响(如裁剪误差、有限尺寸效应等),标度行为的特点(收敛或对数发散)在数据上变得不明显,这需要在未来使用更精确的计算进一步研究,或发展更好的物理性质提取方法。同时,我们的结果暗示了通过(1+1)维共形场论可以对时间矩阵乘积态的临界标度律进行进一步研究。
| [1] |
Holzhey C, Larsen F, Wilczek F. Geometric and renormalized entropy in conformal field theory[J]. Nuclear Physics B, 1994, 424(3): 443-467. Doi:10.1016/0550-3213(94)90402-2 |
| [2] |
Osterloh A, Amico L, Falci G, et al. Scaling of entanglement close to a quantum phase transition[J]. Nature, 2002, 416(6881): 608-610. Doi:10.1038/416608a |
| [3] |
Osborne T J, Nielsen M A. Entanglement in a simple quantum phase transition[J]. Physical Review A, 2002, 66(3): 032110. Doi:10.1103/PhysRevA.66.032110 |
| [4] |
Vidal G, Latorre J I, Rico E, et al. Entanglement in quantum critical phenomena[J]. Physical Review Letters, 2003, 90(22): 227902. Doi:10.1103/PhysRevLett.90.227902 |
| [5] |
Calabrese P, Cardy J. Entanglement entropy and quantum field theory[J]. Journal of Statistical Mechanics:Theory and Experiment, 2004, 2004(6): P06002. |
| [6] |
Calabrese P, Cardy J. Entanglement entropy and quantum field theory:a non-technical introduction[J]. International Journal of Quantum Information, 2006, 4(3): 429-438. Doi:10.1142/S021974990600192X |
| [7] |
Tagliacozzo L, Oliveira T, Iblisdir S, et al. Scaling of entanglement support for matrix product states[J]. Physical Review B, 2008, 78(2): 024410. Doi:10.1103/PhysRevB.78.024410 |
| [8] |
Andersson M, Boman M, Östlund S. Density-matrix renormalization group for a gapless system of free fermions[J]. Physical Review B, 1999, 59(16): 10493-10503. Doi:10.1103/PhysRevB.59.10493 |
| [9] |
Calabrese P, Lefevre A. Entanglement spectrum in one-dimensional systems[J]. Physical Review A, 2008, 78(3): 032329. Doi:10.1103/PhysRevA.78.032329 |
| [10] |
Pollmann F, Mukerjee S, Turner A M, et al. Theory of finite-entanglement scaling at one-dimensional quantum critical points[J]. Physical Review Letters, 2009, 102(25): 255701. Doi:10.1103/PhysRevLett.102.255701 |
| [11] |
Stojevic V, Haegeman J, McCulloch I P, et al. Conformal data from finite entanglement scaling[J]. Physical Review B, 2015, 91(3): 035120. Doi:10.1103/PhysRevB.91.035120 |
| [12] |
Ran S J, Peng C, Li W, et al. Criticality in two-dimensional quantum systems:tensor network approach[J]. Physical Review B, 2017, 95(15): 155114. Doi:10.1103/PhysRevB.95.155114 |
| [13] |
Verstraete F, Cirac J I. Continuous matrix product states for quantum fields[J]. Physical Review Letters, 2011, 104(19): 190405. |
| [14] |
Trotter H F. On the product of semi-groups of operators[J]. Proceedings of the American Mathematical Society, 1959, 10(4): 545-551. Doi:10.1090/S0002-9939-1959-0108732-6 |
| [15] |
Suzuki M, Inoue M. The ST-transformation approach to analytic solutions of quantum systems. Ⅰ:General formulations and basic limit theorems[J]. Progress of Theoretical Physics, 1987, 78(4): 787-799. Doi:10.1143/PTP.78.787 |
| [16] |
Inoue M, Suzuki M. The ST-transformation approach to analytic solutions of quantum systems. Ⅱ:Transfer-matrix and Pfaffian methods[J]. Progress of theoretical physics, 1988, 79(3): 645-664. |
| [17] |
Li W, Gong S S, Zhao Y, et al. Quantum phase transition, O(3) universality class, and phase diagram of the spin-1/2 Heisenberg antiferromagnet on a distorted honeycomb lattice:a tensor renormalization-group study[J]. Physical Review B, 2010, 81(18): 184427. Doi:10.1103/PhysRevB.81.184427 |
| [18] |
Imai T, Nytko E A, BartLetters B M, et al. 63Cu, 35Cl, and 1H NMR in the S= |
| [19] |
Helton J S, Matan K, Shores M, et al. Spin dynamics of the spin-1/2 kagome lattice antiferromagnet ZnCu3(OH)6Cl2[J]. Physical Review Letters, 2007, 98(10): 107204. Doi:10.1103/PhysRevLett.98.107204 |
| [20] |
Olariu A, Mendels P, Bert F, et al. 17O NMR study of the intrinsic magnetic susceptibility and spin dynamics of the quantum kagome antiferromagnet ZnCu3(OH)6Cl2[J]. Physical Review Letters, 2008, 100(8): 087202. Doi:10.1103/PhysRevLett.100.087202 |
| [21] |
Wulferding D, Lemmens P, Scheib P, et al. Interplay of thermal and quantum spin fluctuations in the kagome lattice compound herbertsmithite[J]. Physical Review B, 2010, 82(14): 144412. Doi:10.1103/PhysRevB.82.144412 |
| [22] |
Han T H, Helton J S, Chu S Y, et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet[J]. Nature, 2012, 492(7429): 406-410. Doi:10.1038/nature11659 |
| [23] |
Ryu S, Motrunich O I, Alicea J, et al. Algebraic vortex liquid theory of a quantum antiferromagnet on the kagome lattice[J]. Physical Review B, 2007, 75(18): 184406. Doi:10.1103/PhysRevB.75.184406 |
| [24] |
Ran Y, Hermele M, Lee P A, et al. Projected-wave-function study of the spin-1/2 Heisenberg model on the kagome lattice[J]. Physical Review Letters, 2007, 98(11): 117205. Doi:10.1103/PhysRevLett.98.117205 |
| [25] |
Hermele M, Ran Y, Lee P A, et al. Properties of an algebraic spin liquid on the kagome lattice[J]. Physical Review B, 2008, 77(22): 224413. Doi:10.1103/PhysRevB.77.224413 |
| [26] |
Sindzingre P, Lhuillier C. Low-energy excitations of the kagome antiferromagnet and the spin-gap issue[J]. EPL (Europhysics Letters), 2009, 88(2): 27009. Doi:10.1209/0295-5075/88/27009 |
| [27] |
Iqbal Y, Becca F, Sorella S, et al. Gapless spin-liquid phase in the kagome spin-1/2 Heisenberg antiferromagnet[J]. Physical Review B, 2013, 87(6): 060405. Doi:10.1103/PhysRevB.87.060405 |
| [28] |
Iqbal Y, Poilblanc D, Becca F. Vanishing spin gap in a competing spin-liquid phase in the kagome Heisenberg antiferromagnet[J]. Physical Review B, 2014, 89(2): 020407. Doi:10.1103/PhysRevB.89.020407 |
| [29] |
Liao H J, X ie, Z Y, Chen J, et al. Gapless spin-liquid ground state in the S=1/2 kagome antiferromagnet[J]. Physical Review Letters, 2017, 118(13): 137202. Doi:10.1103/PhysRevLett.118.137202 |
| [30] |
He Y C, Zaletel M P, Oshikawa M, et al. Signatures of Dirac cones in a DMRG study of the kagome Heisenberg model[J]. Physical Review X, 2017, 7(3): 031020. Doi:10.1103/PhysRevX.7.031020 |
 2019, Vol. 36
2019, Vol. 36 


