电子-质子散射几十年来一直是主要的一类高能物理实验，尤其对研究核子结构做出了非常重要的贡献。夸克偶素物理是高能物理研究中的一个重要方向。一来通过研究夸克偶素可以了解重强子的性质，另一方面，由于夸克偶素处于微扰QCD适用能标范围以内，对夸克偶素的研究也是了解认识量子色动力学的重要途径。特别是1995年非相对论量子色动力学NRQCD出现之后^[1]，夸克偶素物理研究有了更坚实的理论基础，引发了持续20多年的研究热潮。人们计算分析夸克偶素在各种高能实验中的产生过程，研究其衰变性质^[2]。

从1974年粲夸克发现以来，夸克偶素遍举产生过程就成为高能物理理论和实验研究的热点课题。它为探究质子内部结构，检验NRQCD因子化，进一步了解微扰QCD提供了很好的研究平台。在实验方面，对电子-质子散射过程中夸克偶素的产生已经做了很多观测，包括夸克偶素遍举产生过程γ^*p→Vp。其中V代表重夸克偶素。如γ^*为实光子，则成为光生(photoproduction)过程；如为虚光子，则对应电生(electroproduction)过程。人们已在各类对撞机上对这些过程进行观察，积累了大量数据，包括铁核固定靶实验中J/ψ遍举光生过程^[3-4]，HERA上J/ψ的遍举光产生^[5-9]，HERA上J/ψ的遍举电产生^[10-13]，HERA上Ƴ的遍举光产生^[5-6]，LHC上J/ψ的遍举光产生^[14-15]，LHC上Ƴ的遍举光产生^[16]等。理论方面，随着有关夸克偶素产生和衰败理论的发展、对核子结构认识的深化、计算能力的提高，在这个领域也取得了丰富的研究成果。

夸克偶素遍举产生过程涉及3个不同的能标：1)光子和质子中部分子相互作用产生正反重夸克对。这属于硬过程，可以用微扰QCD计算。2)正反重夸克对演化到夸克偶素。这个强子化过程包含非微扰效应，可用NRQCD^[1]因子化方案来处理。3)质子和参与到硬过程的部分子间的相互作用。这也属非微扰效应，目前主要采取k_T因子化和共线因子化两种办法处理。

在早期的理论研究中，人们通常采用k_T因子化方案进行计算，主要针对高能极限情况(小x区域)(矢量)夸克偶素衍射产生展开研究。通常通过BFKL^[17-18]重整化群方程对大log(1/x)进行求和。对衍射过程，由于对撞能量远大于其他标度，通常只需考虑振幅虚部的贡献。对于核子部分，则通过引入k_T依赖的“积分前”(unintegrated)胶子分布函数考虑非微软效应，这样最后得到的振幅将正比于普通的胶子分布函数。第一个γ^*p→Vp过程是Ryskin^[19]完成的。后来，很多研究人员在此基础上不断地完善，考虑胶子分布函数斜度的影响、大k_T部分的贡献、相对论修正、实部对截面的贡献等^[20-28]。k_T因子化的方法虽然有着坚实的理论基础，但也存在较大的理论不确定性，并且在k_T因子化下次领头阶计算非常复杂。

另一方面，人们注意到，当质子的入射动量和出射动量不相等(nonforward)时，对应的部分子分布函数和通常意义上的部分子分布函数不同。可以称之为“广义部分子分布函数”(GPDs)。随着Ji和Radyushkin对“深虚康普顿散射”(DVCS)过程^[29-31]和矢量介子遍举产生过程^[32]的研究，GPDs逐渐成为研究的热点。共线因子化方案下对GPDs普适性的严格证明由Collins等完成^[33]。在共线因子化框架下，对重矢夸克偶素光生过程的研究已经做到了微扰次领头阶^[34-37]。对于电生过程，即初态光子虚度不为零的情况，实验上已有大量观察^[10-13]，但理论计算和唯象分析却很有限。本文拟在共线因子化框架下，计算γ^*p→Vp过程，唯象分析HERA上J/ψ和Ƴ遍举产生截面大小随光子虚度Q²及光子-核子能量W_γp变化的关系，并与相应实验结果进行比对。

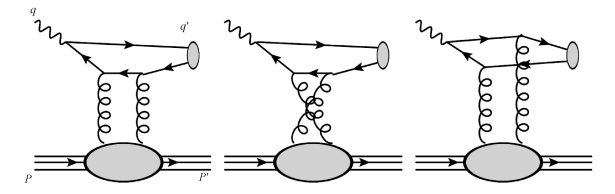
1 计算框架

矢量夸克偶素遍举产生过程的领头阶共有6个费曼图。其中3个如图 1所示，另外3个可在图 1基础上由费米子线反向得到。将初末态粒子动量标记为γ^*(q)p(P)→V(q′)p(P′)。为方便计算和说明，引入“转移动量”和初末态粒子的“平均动量”：

$ \begin{array}{*{35}{l}} \Delta ={{P}^{\prime }}-P, \\ \bar{P}=\frac{P+{{P}^{\prime }}}{2}, \\ \bar{q}=\frac{q+{{q}^{\prime }}}{2}. \\ \end{array} $

(1)

初末态粒子的质量和运动学不变量标记为：

$ \begin{matrix} {{P}^{2}}={{P}^{\prime 2}}={{M}^{2}}, {{q}^{2}}=-{{Q}^{2}}, {{q}^{\prime 2}}=m_{\text{v}}^{2}, \\ s={{(q+P)}^{2}}, t={{\Delta }^{2}}. \\ \end{matrix} $

(2)

在这里，仅对|t|≪W², m_v², Q²区域感兴趣。标度m_v²和Q²的出现，为重夸克偶素遍举产生过程提供了大能标，使得可以用微扰QCD计算对应的部分子过程。选取P三动量方向为z轴正方向，并引入光锥矢量：p^μ=Λ(1, 0, 0, 1), n^μ=(1, 0, 0, -1)/(2Λ)，则可将P, q, Δ进行分解：

$ \begin{array}{*{20}{l}} {{{\bar P}^\mu } = {\mathit{\boldsymbol{p}}^\mu } + \frac{{{M^2} - t/4}}{2}{\mathit{\boldsymbol{n}}^\mu }, }\\ {{{\bar q}^\mu } = - \xi {\mathit{\boldsymbol{p}}^\mu } + \frac{{{Q^2} - {Q^{\prime 2}}}}{{4\xi }}{\mathit{\boldsymbol{n}}^\mu }, }\\ {{\Delta ^\mu } = - 2\eta {\mathit{\boldsymbol{p}}^\mu } + \eta \left({{M^2} - t/4} \right){\mathit{\boldsymbol{n}}^\mu } + \Delta _ \bot ^\mu.} \end{array} $

(3)

这里新引入2个标度参量ξ和η:

$ \begin{align} & \xi \approx \frac{{{Q}^{2}}-{{Q}^{\prime 2}}}{2s+{{Q}^{2}}-{{Q}^{\prime 2}}}, \\ & \eta \approx \frac{{{Q}^{2}}+{{Q}^{\prime 2}}}{2s+{{Q}^{2}}-{{Q}^{\prime 2}}}. \\ \end{align} $

(4)

对于夸克偶素产生过程中的长程效应，采用NRQCD因子化来处理。在计算中需要用到正反重夸克对到相应夸克偶素Fock态的投影^[38]。对于S波自旋三重态，在忽略重夸克间的相对动量，即在非相对论近似领头阶时，投影算符可表示为

$ v{{\left( {{q}_{2}} \right)}_{i}}\bar{u}{{\left( {{q}_{1}} \right)}_{j}}\to -\frac{{{\delta }_{ij}}}{2\sqrt{{{N}_{c}}{{m}_{\text{v}}}}}\frac{{{R}_{s}}(0)}{\sqrt{4\text{ }\!\!\pi\!\!\text{ }}}{{{\not{\epsilon }}}^{*}}\left( {{{\not{q}}}^{\prime }}+{{m}_{v}} \right) $

(5)

式中：i, j表示颜色指标；R_s(0)为夸克偶素径向零点波函数。它的取值既可以由势模型计算，也可以通过将夸克偶素衰变到轻子对过程的理论结果与实验测量相比较得到。

对应我们要计算的过程，显然地，在领头阶参与相互作用的部分子为胶子。核子内胶子的密度分布可以表示为双胶子场对应的光锥矩阵元。选取光锥规范时可以忽略表达式中的P{ }(path-ordering)项，即

$ \int{\frac{\text{d}\lambda }{2\text{ }\!\!\pi\!\!\text{ }}}{{\text{e}}^{\text{i}\lambda x}}\left\langle {{P}^{\prime }}\left| A_{\mu }^{a}\left( -\frac{\lambda n}{2} \right)A_{\nu }^{b}\left( \frac{\lambda n}{2} \right) \right|P \right\rangle = \\ -\frac{1}{2}\frac{{{\delta }^{ab}}}{N_{c}^{2}-1}\frac{1}{(x-\eta +\text{i}\varepsilon )(x+\eta -\text{i}\varepsilon )}\times \text{ }\left( g_{\bot }^{\mu \nu }{{F}^{g}}(x, \eta , t)+\text{i}\epsilon _{\bot }^{\mu \nu }\text{ }\ {{{\tilde{F}}}^{g}}(x, \eta , t) \right)\text{ }. $

(6)

式中：a, b是胶子颜色指标；g_⊥^μν=g^μν-p^μn^ν-n^μp^ν；∈_⊥^μν=∈^npμν。F^g(x, η, t)和${{{\tilde{F}}}^{g}}$(x, η, t)的定义与文献[39]相同。事实上通过计算可以发现，在|t|≪W², m_v², Q²区域，${{{\tilde{F}}}^{g}}$(x, η, t)项并没有贡献。这个结论与文献[40]一致。

2 解析结果

首先考虑Δ_⊥=0的情形，Δ_⊥≠0的情况将在本节最后讨论。Δ_⊥=0时，入射光子和出射重介子的运动方向都平行于z轴。因此，它们的横向极化矢量可以表示为∈^(±)=(0, 1, ±i, 0)/ $\sqrt 2 $ ，光子的纵向极化表示为∈_γ⁰=(q_z, 0, 0, E_z)/Q，夸克偶素的纵向极化则为∈_v⁰=(q′_z, 0, 0, E′_z)/m_v。用λ表示光子的极化，λ′表示夸克偶素的极化，$\mathcal{M}$^λλ′为对应的螺旋度振幅。通过标准的场论计算可得

$ {{\mathcal{M}}^{++}}=-\frac{16g{{e}_{q}}{{m}_{\text{v}}}{{\text{ }\!\!\pi\!\!\text{ }}^{3/2}}{{\alpha }^{1/2}}{{\alpha }_{s}}}{m_{\text{v}}^{2}+{{Q}^{2}}}\frac{1}{\eta }\cdot \left[ {{\mathcal{H}}^{\text{g}}}\psi \left( {{P}^{\prime }}, M \right)\not{n}\psi (P, M)+ \right.\left. \text{i}{{\varepsilon }^{g}}\psi \left( {{P}^{\prime }}, M \right)\frac{{{\sigma }^{n\Delta }}}{2M}\psi (P, M) \right]. $

(7)

之外，螺旋度振幅$\mathcal{M}$^--=$\mathcal{M}$⁺⁺, ${{\mathcal{M}}^{00}}=-\frac{Q}{{{m}_{\text{v}}}}{{\mathcal{M}}^{++}}$，其余的螺旋度振幅为0。这意味着初态是实光子的情况下，末态的夸克偶素全部只有横向极化，这符合强相互作用螺旋度守恒的要求。式(7)中的$\mathcal{H}$^g和ε^g定义为

$ \begin{array}{*{35}{l}} {{\mathcal{H}}^{g}}=\int_{-1}^{1}{\text{d}}x{{H}^{g}}(x, \eta , t|)\left[ \frac{1}{x-\eta +\text{i}\epsilon }-\frac{1}{x+\eta -\text{i}\epsilon } \right], \\ {{\varepsilon }^{g}}=\int_{-1}^{1}{\text{d}}x{{E}^{g}}(x, \eta , t)\left[ \frac{1}{x-\eta +\text{i}\epsilon }-\frac{1}{x+\eta -\text{i}\epsilon } \right]. \\ \end{array} $

(8)

注意，H^g(x, η, t)和E^g(x, η, t)是x的偶函数。在向前(forward)极限下H^g(x, η, t)可以过渡到普通的部分子分布函数：H^g(x, 0, 0)=xg(x)。对于E^g(x, η, t)则没有类似性质。

根据式(7)，可以计算出Δ_⊥=0处的微分截面，即

$ {{\left. \frac{\text{d}\sigma \left( {{\gamma }^{*}}p\to Vp \right)}{\text{d}\Delta _{\bot }^{2}} \right|}_{{{\Delta }_{\bot }}=0}}=\frac{{{\left| {{R}_{s}}(0) \right|}^{2}}}{16\text{ }\!\!\pi\!\!\text{ }s\left( s-m_{\text{v}}^{\text{2}} \right)}\frac{256{{\text{ }\!\!\pi\!\!\text{ }}^{2}}\alpha \alpha _{s}^{2}}{27}\frac{{{m}_{v}}}{{{\left( m_{\text{v}}^{\text{2}}+{{Q}^{2}} \right)}^{2}}}\times \text{ }\frac{\left| -\left( 1-{{\eta }^{2}} \right){{\mathcal{H}}^{g}} \right.+{{\left. {{\eta }^{2}}{{\varepsilon }^{g}} \right|}^{2}}}{{{\eta }^{2}}\left( 1-{{\eta }^{2}} \right)}\left( 1+\frac{{{Q}^{2}}}{m_{\text{v}}^{2}}\epsilon (y) \right). $

(9)

式(9)第3行中的两项分别表示横向极化光子和纵向极化光子对微分截面的贡献。参数∈是虚光子的极化参数。在电子-核子散射中，它可以表示成$y=\frac{P\cdot q}{P\cdot k}$的函数，即：∈(y)=$(1-y)/(1-y+\frac{1}{2}{{y}^{2}})$在大部分夸克偶素遍举产生实验中，∈的值非常接近1。

对截面Δ_⊥依赖的描述通常有两种分析方法。第一种是GPDs的t依赖假设，即假定${{H}^{q,g}}(x, \eta , t)=\frac{1}{2}F_{1}^{q,g}(t)H(x, \eta , 0)$。对于价夸克的情况，F₁^q(t)可以通过质子和中子的电磁形状因子组合得到。对于胶子的情况，F₁^g(t)和G^μαG_μ^β的形状因子相关，而这是一个无法直接测量的量。虽然可以通过引入模型的方法对G^μαG_μ^β的形状因子进行估计，但这样做会引入额外的理论不确定性。因此我们采用第2种办法，假设截面对Δ_⊥满足如下关系

$ \frac{\text{d}\sigma }{\text{d}\Delta _{\bot }^{2}}=\text{(}{{\left. \frac{\text{d}\sigma }{\text{d}\Delta _{\bot }^{2}} \right|}_{{{\Delta }_{\bot }}=0}}\text{)}{{\text{e}}^{-b\Delta _{\bot }^{2}}}. $

(10)

参数b称为“斜率”(slope)参数。在坡密子(Pomeron)理论中，b(W)=b₀+4α′ln(W/W₀)。式(10)中各参数可以通过对实验数据的拟合得到。

3 数值结果

这部分考虑J/ψ和Ƴ在HERA上的产生。为分析重夸克质量引起的不确定性，取粲夸克质量m_c={1.4, 1.5, 1.6} GeV，底夸克质量m_b={4.8, 4.9, 5.0} GeV。因子化能标μ=r(m_v²+Q²)/4。为估计能标变化所带来的不确定性，r取3个值：{0.5, 1.0, 2.0}。计算强相互作用耦合参数取次领头阶时的值:$\frac{{{\alpha }_{s}}(\mu )}{4\text{ }\!\!\pi\!\!\text{ }}=\frac{1}{{{\beta }_{0}}L}-\frac{{{\beta }_{1}}\ln L}{\beta _{0}^{3}{{L}^{2}}}$。对于夸克偶素径向零点波函数，采用势模型^[41]的结果，即：|R_s^J/ψ(0)|²=0.810 GeV³和|R_s^Ƴ(0)|²=6.477 GeV³。

在截面的数值计算中，还需要对GPDs进行数值估计。对于H^g(x, η, t)，依据“双分布”(double distributions)模型^[42-44]进行数值模拟。具体计算方法可参照文献[44]的第2部分。图 2展示不同η和μ²下，$\mathcal{H}$^g的实部和虚部之比。可以发现，随着η和μ²的减小，虚部贡献所占的比例逐渐增大。这和高能极限下(衍射过程)，振幅虚部对截面贡献占主导的结论是一致的。但在我们的唯象学分析中，μ=r(m_v²+Q²)/4，因此实部的贡献会随着光子虚度的增大(偏离衍射)而增大。对于E^g(x, η, t)，目前尚无很好的模型可用于唯象学计算。但根据式(9)，ε^g项有系数η²压低。因此，我们将这部分贡献忽略。这也是对DVCS和重夸克偶素遍举产生过程做唯象学研究时普遍采取的做法。

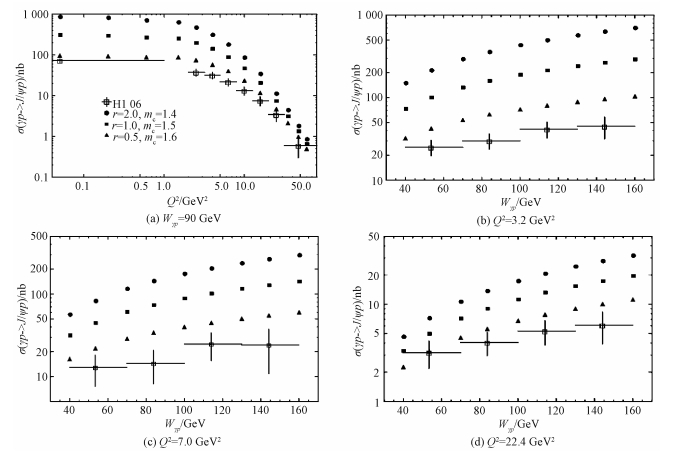
下面分析J/ψ在HERA上的产生。斜率参量b及t取H1实验组所取的实验参数^[13]。图 3展示J/ψ遍举产生截面对Q²及W_γp的依赖关系。其中，误差棒表示H1实验组的实验结果^[13]；不同形状的实心点表示我们的计算结果及理论不确定性。圆点组成的上边界对应的参数选取为：r=2.0, m_c=1.4 GeV；处于中间的方形点对应：r=1.0, m_c=1.5 GeV；三角形点组成的下边界对应：r=0.5, m_c=1.6 GeV。图 4(a)~4(d)分别对应W_γp=90 GeV，Q²=3.2 GeV²，Q²=7.0 GeV²和Q²=22.4 GeV²。可以看出，计算结果较实验数据普遍偏大，尤其是当W_γp较大或Q²较小时。在同样情况下，能标和质量引起的不确定度也相当大。究其原因，可以用小x区域胶子部分子分布函数随能标的增大而迅速增大来解释。

对Ƴ在HERA上的遍举产生，由于缺少相应实验数据，我们简单地取斜率参量b=4.4 GeV^-2，同时假定总截面$\sigma =\frac{1}{b}\left( \frac{\text{d}\sigma }{\text{d}\Delta _{\bot }^{2}}\left| _{{{\vartriangle }_{\bot }}=0} \right. \right)$。图 4(a)展示光产生情况下实验和理论的结果。图中各标记的含义和J/ψ的情况类似，误差棒表示实验测量结果^[5-6]，圆点组成的上边界对应的参数选取为：r=2.0, m_b=4.8 GeV，处于中间的方形点对应：r=1.0, m_b=4.9 GeV，三角形点组成的下边界对应：r=0.5, m_b=5.0 GeV。图 4(b)预言了W_γp=143 GeV时，总截面σ(γ^*p→Ƴp)的Q²依赖关系，这可留待未来实验数据分析对此进行验证。可以发现，相较于J/ψ，Ƴ的产生截面对能标的依赖性相对较弱，在光产生情况下，理论大致可以解释实验。

4 总结

本文在共线因子化的框架下，计算微扰量子色动力学领头阶下重夸克偶素在电子-质子散射过程中的遍举产生过程，给出相应振幅和截面的解析表达式。还唯象分析HERA实验中J/ψ和Ƴ遍举产生截面对光子虚度Q²和撞能量W_γp的依赖关系，并与实验结果进行比较。发现对于J/ψ遍举产生，理论计算值明显大于实验测量值，特别是在小x区域。对于Ƴ遍举光产生，在考虑实验和理论误差的情况下，可以解释实验。通过取不同的重夸克质量和不同的因子化能标，估计理论不确定性。发现在小x区域，能标引起的不确定性非常大。这一方面说明在小x区域，胶子分布函数本身有很大的不确定度，另一方面说明在这些过程中，高阶修正的贡献非常大，未来有必要进一步研究。

最后需要特别指出的是，对夸克偶素在电子-质子碰撞中遍举产生的研究，非常有益于了解推广的部分子分布函数(GPD)。