随着计算机技术的发展,三维建模技术在工程建模、数字城市、文物保护和自动驾驶等领域的应用日益广泛。而如何获取完整的物体表面信息则是其中最为基础的课题之一。由于点云采集设备有限的视角、物体的遮挡以及采集环境等限制,通常来说,需要多角度、多批次采集才能获取物体完整的表面信息。点云配准则是把这些多批次、多角度获取到的点云数据整合到同一个视角中去的过程。从数学角度讲,每个点云数据都有其自身的坐标系。点云配准需要解决的问题则是通过坐标系变换,将这些不同坐标系的点云数据转换到同一个坐标系下。
作为计算机视觉的基本问题之一,点云配准研究在过去的二三十年里取得了丰硕的成果[1]。其中,最为常用的点云配准算法是ICP算法(iterative closest point)[2]。ICP算法采用迭代最优化的思想,每次迭代追求目标点云与源点云之间距离最小,最终算法收敛到一个当前最优状态。这种算法思想简单,容易实现,获得结果的精度高。然而,在初始位置不理想的情况下,这种算法获得的当前最优结果有可能只是局部最优而非全局最优。而且,这种方法也容易受到噪声和离群点的影响,最终导致配准失败。同时,由于每次迭代都需要计算2个点云之间的最近点,因而计算复杂度较高。这些缺点很大程度上限制了ICP的应用场景。为改善这些缺点,一大批方法被提出[1, 3-10]。其中,Masuda等[5],Godin[6]及Weik[7]提出的基于下采样的方法有效改善了ICP的运行效率,却导致配准的精度下降。Bosse和Zlot[11],Gelfand等[10]及Segal等[9]分别引入点到线、点到面和面到面的距离替代ICP中点到点的距离以改善其效率。然而,这些方法都需要配准点云对象有比较明显的线面特征(如室内场景)。Yang等[8]引入分支限界的思想提出一种获得全局最优的ICP改进算法,改善了局部最优的缺点;但在实验中,运算时间过长,效率过低。
针对ICP运行效率低下和易受噪声与离群点影响的缺点,本文提出一种基于高斯曲率的改进算法。该方法利用高斯曲率不仅过滤掉大量配准非关键点,提高了ICP算法运行效率;而且也过滤掉大部分的噪声点和离群点,增强了算法的健壮性。特别地,本方法获得上述优点的同时并不降低配准的精度。相较于同样利用表面特征如线、面等的改进算法,本方法只需要点云对象有一定的曲率特征(凸出、凹陷、拐角、边线等等),因而适应性更为广泛。同时,本方法还具有良好的扩展性,很容易移植到其他ICP改进方法上以获得综合的优点。
1 背景知识在刚体变换中,点云配准是指求2个点云之间的旋转矩阵和平移向量,将源点云变换到与目标点云相同的坐标系下的过程。整个过程表示为
| $ \boldsymbol{P}_{\mathrm{t}}=\boldsymbol{R} \boldsymbol{P}_{\mathrm{s}}+\boldsymbol{t}, $ | (1) |
式中:Pt为目标点云,Ps为源点云,R代表旋转矩阵,t代表平移向量。经典的ICP算法通过不断迭代减小两点云变换后的误差,直到收敛。其目标函数为
| $ E\left( {{\mathit{\boldsymbol{P}}_{\rm{t}}}, {\mathit{\boldsymbol{P}}_{\rm{s}}}} \right) = \frac{1}{{{N_p}}}\sum\limits_{i = 1}^{{N_p}} {\parallel \mathit{\boldsymbol{RP}}_{\rm{s}}^i + \mathit{\boldsymbol{t}} - \mathit{\boldsymbol{P}}_{\rm{t}}^i{\parallel ^2}}, $ | (2) |
式中:Np代表 2个点云重叠区中点的数量,Psi和Pti为源点云与目标点云中对应的点对。根据式(2)可知,如果减小Np,算法的运行效率便会得到相应的提升。在这种思路下,下采样策略[3, 5-7]被提出以提高ICP的运行效率。这些下采样策略减小了Np的值,但也因为下采样导致待配准点云的密度下降,最终导致配准结果的精度因此受损。为改善这个缺点,本文引入高斯曲率以减少参与配准的点数量。同时,保证剩余的点云密度不变。
作为基本的几何量之一,曲率描述曲面表面的弯曲程度。其中,高斯曲率在物体表面曲率中有着特殊地位。根据高斯绝妙定理,高斯曲率是内禀的。这意味着高斯曲率在保距变换中保持不变。记曲面第一和第二基本形式分别为 < E, F, G>和 < L, M, N>, 则高斯曲率可以表示成
| $ K=\frac{L N-M^{2}}{E G-F^{2}}. $ | (3) |
表面曲率是计算机视觉和计算机图形学的重要研究课题之一。在这个方面,同样产生了大量关于曲率计算的成果[12-17]。马骊溟等[18]提出一种计算散乱点云高斯曲率的方法。此方法根据最小二乘法求出点邻域内的曲面模型,然后再利用梯度法搜索曲面上高斯曲率极值点。接着将该点作为搜索曲率极值点的初始点,并沿着主曲率方向搜索该点邻域其余主方向上的极值点。这个方法既继承了传统方法中拟合二次曲面模型并求极值的方法[19],又避免了计算全部点,提高了计算效率。Zhang等[17]提出一种估计邻域点的法向量,而后利用欧拉公式将主曲率求解问题转化成最小二乘问题的方法。这些方法对本算法中高斯曲率的计算有直接的指导意义。
2 基于高斯曲率的ICP优化配准算法本算法分为两个关键步骤。第一步,求取高斯曲率并根据高斯曲率过滤配准非关键点。第二步,在配准关键点上应用ICP算法,获得配准结果。关于高斯曲率的估计方法有很多,其中Zhang等[17]提出的算法,原理清晰,效率高且结果较为精确。本文将以此算法为例介绍高斯曲率的计算过程。
1) 首先,设点p及其周围邻域内m个最近邻点为qi(i=1, 2, 3,…, m)。设N为点p的法向量,Mi为点qi的法向量,则p点相对于qi的法曲率kni估计如下
| $ k_{n}^{i}=-\frac{\sin \beta}{\left|p q_{i}\right| \sin \alpha}, $ | (4) |
式中:α为向量N与向量pqi之间的夹角;β为向量N与向量Mi之间的夹角;|pqi|为p与qi之间的欧氏距离。
2) 根据欧拉公式,法曲率与主曲率有以下关系
| $ k_{n}^{i}=k_{1} \cos ^{2}\left(\theta_{i}+\theta\right)+k_{2} \sin ^{2}\left(\theta_{i}+\theta\right), $ | (5) |
其中:i=1, 2, …, m,k1和k2是主曲率;θi+θ为点p过qi的法截线的切线与主方向的夹角。
3) 令
| $ \mathop {\min }\limits_{{k_1}, {k_2}, \theta } \sum\limits_{i = 1}^m {} {\left[ {{U_i} - k_n^i} \right]^2}, i = 1, 2, \cdots , m. $ | (6) |
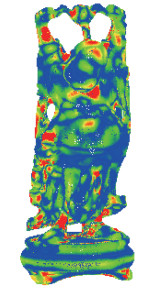
从以上计算过程可以看出,在点云数据中,点的高斯曲率定义于其邻域上。一般而言,在大的邻域上计算出的高斯曲率其数值相对小,比较稳定,但运算时间较长;而小的邻域上计算出的高斯曲率其数值相对大,而稳定性稍差,运算时间较短。在实际配准场景中,一般邻域半径的选择应能基本覆盖表面的弯曲特征。图 1给出高斯曲率在Budda模型上的分布(由蓝到红表示其高斯曲率由小到大),点的邻域设为0.001而点与点之间的间隔约为0.0003。同时可以看出,高斯曲率较大的地方在于角、凹陷等弯曲特征比较明显的区域。而这些区域则是点云配准的关键区域。
|
Download:
|
| 图 1 Buddha模型表面的高斯曲率分布图 Fig. 1 Distribution of Gaussian curvature on the surface of Buddha model | |
在获取高斯曲率之后,设置阈值过滤高斯曲率过高和过低的点。过低的点,一般位于平坦的面上,对配准贡献不大;而过高的点,则是噪声点或离群点,对配准有害。
经过高斯曲率过滤之后,剩余的点只有原来很少的一部分。这些剩余的点被认为是物体表面的关键点。在2个点云数据的关键点上应用ICP,不仅能显著提高ICP运行速度,而且使整个算法有更强的健壮性。同时,由于这些关键点在过滤之后依然保持原来的密度,这样应用ICP之后,并不会因为过滤而导致配准精度下降。
3 实验与分析 3.1 实验说明根据引入高斯曲率的目的,本文将从以下方面评估本方法的有效性和健壮性:不同大小的点云数据、不同的噪声情况和离群点情况。第1部分实验中,使用公共数据集中的Standford Bunny、Armadillo以及Buddha模型评估本算法的有效性;使用Standford Bunny分别在100%的离群点和100%的高斯噪声环境下进行实验,以评估本方法的抗噪声和离群点的能力。第2部分实验中,使用实际采集的工程数据验证本算法对ICP算法健壮性的改进。同时,通过在不同采样率下本算法与ICP执行时间的比较,验证本算法对ICP在执行时间方面的提升。尽管本文算法是对ICP的改进算法,为了描述方便,以下将经典的ICP称为ICP,而将本文提出的改进算法称为本方法。
本文所有实验以C++来实现,运行在I5-3320M CPU, 8G内存的PC机上。第1部分实验所使用的数据来自于佐治亚理工学院提供的公共数据集。第2部分实验使用的工程数据扫描于北京香山公园的一处建筑,扫描仪器为Leica P30地面激光扫描仪。
3.2 实验结果与分析 3.2.1 公共数据实验第1组实验评估在一般条件下,与ICP相比,本方法的运行效率及配准精度。其结果如图 2所示,运行时间及配准精度记录于表 1前3行。从图 2可以看出,本方法与ICP都能获得较好的结果。从表 1也可以看出:以均方根误差(root mean square error, RMSE)衡量配准精度,对于图 2的实验,本方法与ICP取得结果精度相当,但本方法在运行时间上更为快速。本组实验表明,在保证精度的前提下,本方法确实获得了效率上的较大提升。

|
Download:
|
| 图 2 本方法在公共数据集下的表现 Fig. 2 Results of the proposed method on the public models | |
|
|
表 1 本方法与ICP的均方根误差(RMSE)和处理时间 Table 1 RMSE and time consumption of the proposed method and ICP |
第2组实验评估在重噪声和离群点的条件下,与ICP相比,本方法抗噪声及离群点的能力。其结果如图 3所示(其中,左、中、右分别为初始位置、ICP算法结果和本方法结果),运行时间及配准精度记录于表 1后2行。图 3(a)实验中添加100%离群点,图 3 (b)实验中添加100%标准方差为5倍点间距的高斯噪声。可以看出,在添加100%的离群点情况下ICP并不能给出正确的匹配结果,本方法给出的结果却仍然非常精细;在添加100%的高斯噪声情况下,ICP最终获得一个次优的结果,而本方法则达到更好的效果,这说明本方法能更好地处理大量离群点和噪声场景下的配准问题。从表 1中也可以看出,存在噪声和离群点情况下,本方法要比ICP更加健壮。

|
Download:
|
| 图 3 本方法在离群点和噪声情况下的表现 Fig. 3 Results of the proposed method under the outlier and noise circumstance | |
从表 1运行时间来看,本方法比ICP有显著提高,而这种提高随着配准点云数据量的增加越来越明显(这一点会在图 4所示实验中进一步说明)。同时,噪声和离群点的增加并不会影响本方法的运行时间。在配准精度方面,本方法在重噪声及离群点的情况下,依然保持了较高的配准质量。这一点,相较于ICP来说有非常大的改进。

|
Download:
|
| 图 4 本方法与ICP在建筑物数据下配准效果对比 Fig. 4 Results of the proposed method and ICP on the building model | |
本部分实验使用实际工程数据以验证本方法对ICP健壮性及运行效率的改进。在图 4中,图 4 (a)~图 4 (d)给出本方法对实际工程数据配准各阶段的结果;图 4 (e)为直接使用ICP对原始数据进行配准的结果;图 4 (f)给出将ICP的配准结果作用于表面配准关键点上的效果。从最终结果图 4 (d)可以看出,本方法能较好地配准原始数据,而在图 4 (e)中可以看出在拱门边缘、中间靠上的匾额处明显出现配准不一致的边缘凸起。与图 4 (c)的对比,能清晰地看到图 4 (f)中2个点云数据上出现比较明显的偏差。该组实验表明本方法更注重点云中的关键点在配准中的作用,从而提高了ICP的健壮性。
本文使用图 4 (a)中所示的原始数据进行不同比例的随机下采样并进行实验,以评估对于不同大小的点云数据本方法对ICP运行效率方面的提升。结果如表 2所示。可以看出随着数据量的提升,本方法对ICP的效率提升越来越明显。这也验证了本方法提取配准关键点以提高ICP运行效率的有效性。
|
|
表 2 不同采样率下的运行时间表 Table 2 Time consumption at different sampling rates |
本文提出的方法显著地提高了ICP的运行速度,增强了ICP在噪声点和离群点情况下的健壮性。不同于基于一致性[21]及法向量[3, 5]等下采样策略,本方法在减少运算数据量的同时并不会使得配准之后的精度下降。同时,相较于ICP而言本方法更关注关键点在配准中的作用,这个特点能一定程度上改善ICP陷入局部最优的缺点。在运行效率方面,由于ICP的特性,每次迭代源点云中的每一个点都需要访问目标点云中最近的点。而本文引入的高斯曲率对2个点云中的点则只需一次计算,计算之后过滤出的关键点只有相对原始数据来说非常少的一部分。而这部分的迭代由于其数量非常少,其运行速度非常快。因此,随着数据量增大,本方法获得的运算时间效率的提升会越来越明显。
此外,相较于同样使用物体表面特征(线、面)的ICP改进算法来说,本方法计算过程中不需显式地提取特征而且适用场景更加广泛。同时,本方法提出的是对ICP算法前序处理的改进,这种改进可以很方便地移植到ICP其他的改进算法(如Sparse-ICP和Go-ICP)上,以改善其效率和健壮性。
然而,由于本方法利用物体表面的高斯曲率特征以提取配准关键点,而高斯曲率的估计依赖于点邻域的定义。因此为了获得更明显的关键点,需要设置合适的邻域以及高斯曲率阈值。这与ICP相比需要额外的工作。此外,如果物体表面的曲率特征过于复杂(如图 4 (a)的上半部分),则本方法将退化为ICP方法。
4 总结本文提出一种基于高斯曲率的ICP改进方法。从实验结果来看,本方法实现了对ICP的以下改进:第一,本方法在保证精度的情况下,实现了算法效率的明显提升,而这种提升在大数据量的场景下会特别明显;第二,在重噪声和离群点的条件下,本方法表现出很强的抗噪性和离群点耐受性;第三,本方法对配准场景具有广泛的适用性而且可以很容易移植到ICP其他改进算法上去,以提高其运行效率和健壮性。
| [1] |
Colas F, Siegwart R. A review of point cloud registration algorithms for mobile robotics[M]. Boston: Now Publishers Inc, 2015: 1-104.
|
| [2] |
Besl P J, Mckay N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 14(2): 239-256. |
| [3] |
Rusinkiewicz S, Levoy M. Efficient variants of the ICP algorithm[C]//Proceedings of 3rd International Conference on 3D Digital Imaging and Modeling. Quebec City: IEEE Computer Society, 2002: 145-152.
|
| [4] |
Mavridis P, Andreadis A, Papaioannou G. Efficient sparse ICP[M]. Amsterdam: Elsevier Science Publishers B V, 2015: 16-26.
|
| [5] |
Masuda T, Sakaue K, Yokoya N. Registration and integration of multiple range images for 3-D model construction[C]//Proceedings of International Conference on Pattern Recognition. Vienna: IEEE Computer Society, 1996: 879-883. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=546150
|
| [6] |
Godin G. Three-dimensional registration using range and intensity information[C]//International Society for Optics and Photonics. Videometrics Ⅲ. Boston: Videometrics Ⅲ, 1994: 279-290. http://www.researchgate.net/publication/239665616_Three-dimensional_registration_using_range_and_intensity_information
|
| [7] |
Weik S. Registration of 3-D partial surface models using luminance and depth information[C]//Proceedings of 3-D Digital Imaging and Modeling. Montreal: IEEE Computer Society, 1997: 93-100.
|
| [8] |
Yang J, Li H, Jia Y. Go-ICP: solving 3D registration efficiently and globally optimally[C]//Proceedings of IEEE International Conference on Computer Vision. Sydney: IEEE Computer Society, 2013: 1 457-1 464.
|
| [9] |
Segal A, Hähnel D, Thrun S. Generalized-ICP[C]//Proceedings of Robotics: Science and Systems V. Seattle: The MIT Press, 2009: Doi: 10.15607/RSS.2009.V.021.
|
| [10] |
Gelfand N, Rusinkiewicz S, Ikemoto L, et al. Geometrically stable sampling for the ICP algorithm[C]//Proceedings of International Conference on 3-D Digital Imaging and Modeling. Banff: IEEE Computer Society, 2003: 260-267.
|
| [11] |
Bosse M, Zlot R. Keypoint design and evaluation for place recognition in 2D lidar maps[J]. Robotics & Autonomous Systems, 2009, 57(12): 1. |
| [12] |
Magid E, Soldea O, Rivlin E. A comparison of Gaussian and mean curvature estimation methods on triangular meshes of range image data[J]. Computer Vision & Image Understanding, 2007, 107(3): 139-159. |
| [13] |
Alboul L, Van Damme R. Polyhedral metrics in surface reconstruction: tight triangulations[C]//Proceedings of the 6th IMA Conference Conference on the Mathematics of Surfaces. London: Clarendon Press, 1994: 171-200.
|
| [14] |
Watanabe K, Belyaev A G. Detection of salient curvature features on polygonal surfaces[J]. Computer Graphics Forum, 2001, 20(3): 385-392. Doi:10.1111/1467-8659.00531 |
| [15] |
Taubin G. Estimating the tensor of curvature of a surface from a polyhedral approximation[C]//Procedings of International Conference on Computer Vision. Cambridge: IEEE Computer Society, 1995: 902-907. http://dl.acm.org/citation.cfm?id=840020
|
| [16] |
Lin C, Perry M J. Shape description using surface triangulation[J]. Proceedings of the IEEE Workshop on Computer Vision, 1982, 26(1): 51-65. |
| [17] |
Zhang X, Li H, Cheng Z, et al. Robust curvature estimation and geometry analysis of 3D point cloud surfaces[J]. Journal of Information & Computational Science, 2009, 6(5): 1 983-1 990. |
| [18] |
马骊溟, 徐毅, 李泽湘. 基于高斯曲率极值点的散乱点云数据特征点提取[J]. 系统仿真学报, 2008, 20(9): 2 341-2 344. |
| [19] |
吕震, 柯映林, 孙庆, 等. 反求工程中过渡曲面特征提取算法研究[J]. 计算机集成制造系统, 2003, 9(2): 154-157. Doi:10.3969/j.issn.1006-5911.2003.02.014 |
| [20] |
Zhang X, Li H, Cheng Z, et al. Curvature estimation of 3d point cloud surfaces through the fitting of normal section curvatures[C]//Proceedings of AsiaGraph. Tokyo, 2008: 72-79.
|
| [21] |
Turk G. Zippered polygon meshes from range images[C]//Proceedings of Conference on Computer Graphics and Interactive Techniques. Orlando: ACM, 1994: 311-318. http://dl.acm.org/citation.cfm?id=192241
|
 2019, Vol. 36
2019, Vol. 36 


