地热能是来源稳定的可再生清洁能源,储量巨大、无污染。开发利用地热能既能满足人类的能量需求,又能保护地球环境免遭破坏,因而对国民经济的可持续发展意义重大。地热能开发的重中之重是地热发电, 其能源利用系数远高于水力、风力、太阳能发电和地热直接利用[1-3]。由于地热电站可不受季节、气候、昼夜等自然条件的影响而不间断运行,地热发电可以作为国家电网的基础载荷,也易于调峰和实施热电联供[4-5]。目前地热能的开发主要是中低温地热能的直接利用,地热发电没有得到应有的发展[6]。
1 研究背景地热资源按其成因和产出条件可分为水热型和干热岩型[7]。水热型地热资源赋存于高渗透性的孔隙或裂隙介质中,与年轻火山活动或高热流背景相伴生形成高温水热系统,而处于正常或偏低热流背景下的地下水循环通常形成中低温水热系统,主要用于地热能的直接利用。干热岩型地热资源赋存于地下较深处的高温但低渗透性岩体中,原则上不受地区分布限制,但其开采需要借助人工压裂进行储层改造(reservoir stimulation),进而通过注水循环形成增强型地热系统(enhanced geothermal system,EGS)[8]。
近年来EGS的研究和开发广受关注,在美国、英国、法国、德国、瑞士、日本、澳大利亚等国家已经进行了EGS工程试验[5-6, 9-11],但商业运行EGS电站的成功案例还很少[1]。EGS是一个有广泛应用前景,值得深入研究的问题。EGS发电需要满足两个主要条件:一个是要从储层中提取出足够高温度的能量,另一个是采热过程中要有足够的流体流量供给[12]。一般来讲,EGS选用地下3~10km深处较高温度的干热岩作为储层。但因干热岩通常具有低孔隙度、低渗透率的特点,需要对储层进行人工压裂形成流体运移通道,以满足EGS发电的流体流量要求,并保证流体在储层内的运移过程中能够和围岩进行充分的热交换。
EGS问题是一个典型的多区域、多物理场耦合问题。在由注水井、生产井、孔隙储层、不可渗透围岩组成的多区域EGS中,不同区域服从不同的控制方程,但在区域边界上要满足物理上合理的连接条件。同时,在EGS模拟中,温度场和渗流场必须耦合求解,有时还涉及与固体变形、组分输运的联合求解。国内外文献中发表的代表性研究工作包括:1)Gong等[13]对华北油田伴生地热发电项目的注水-采液过程进行渗流和传热耦合的数值模拟,定量研究注水速度、注水温度对地热田温度随时间变化的影响;2)Bataillé等[14]数值模拟法国Soultz-sous-Forets EGS地热田中的自然对流和强迫对流,揭示裂隙岩石中自然对流对维持地热田温度进而延长地热电站寿命的作用;3)Blcher等[15]研究德国一对地热注水井和生产井的长期工作状态,预测这对地热井将在使用3.6a后开始发生热贯通(thermal breakthrough);4)Zhou和Hou[16]提出一个模拟水力压裂过程的数值模型,研究裂隙的动态扩张过程及孔隙流体与裂隙流体之间的质量、动量交换;5)Jiang等[17-18]以及Chen和Jiang[19]基于Brinkman方程数值模拟EGS的渗流传热过程,考虑渗透率及围岩与孔隙流体间热不平衡对EGS寿命的影响,Cao等[20]进而研究多种地热井布局及构造应力作用下注水流量与采热效率、EGS寿命之间的关系;6)针对以CO2为工质的EGS,Luo等[21]研究井中湍流及其与储层渗流的耦合,Li等[22]用实验方法研究稳态自然对流对采热的影响,Jiang等[23]比较不同井型(包括水平井)对采热的影响;7) Zeng等[24-26]数值模拟Desert Peak、羊八井地热田的采热过程,包括水平井和垂直裂缝情形; 8)Pruess[27-28]从可压性、能量提取率和流体损失等角度对比基于CO2和水两种工质的EGS; 9)Saeid等[29-31]对低温地热系统进行一维和两维耦合模拟,考虑层流和湍流热导率的不同,通过不同的参数对比,得出地热田寿命依赖于孔隙度、流量、井距、储层温度、注水温度的定量关系;10)Huang等[32]研究双井EGS井中湍流和储层达西流的耦合,发现井中压力变化主要由静水压力主导,进而以一维井内流动假设为基础得到流体温度的解析解。
在典型EGS工作条件下,井内流动以湍流主导。例如,在一个贯穿500m储层的半径为0.15m的注水井或生产井中,如果质量流量为50kg/s,容易证明,只有在井底以上5m范围内井内流动的雷诺数小于2200, 即圆形管道内层流向湍流过渡的临界雷诺数,而在99%的井深范围内井内流动都处于湍流状态。为考虑EGS涉及的井内湍流作用,采用湍流模型进行数值模拟是一个可行的途径,但需要注意不同湍流模型适用的条件。例如,k-ε模型数值稳定性好,尤其适用于大雷诺数流动,但在固体边界附近区域表现较差,而k-ω模型能较好刻画边界附近湍流,但对入口湍流条件较为敏感,导致数值稳定性较差[33-34]。结合k-ε与k-ω两种湍流模型的优点,Menter[35]提出SST(shear stress transport)模型。此外,还有通过引入阻尼函数在边界附近区域对k-ε模型修正而建立的小雷诺数模型[33]。
前人研究工作中,对多区域耦合采用简化近似的方法,或者直接指定区域界面的速度或压力[21],或者以Brinkman方程同时描述井内区域和储层区域(通过孔隙度和渗透率不同取值体现区域差异,将井内区域看作渗透率趋近无穷大情形)[17-20]。由于Brinkman方程只对高孔隙度介质成立[36],将其外推应用于低孔隙度EGS储层并没有足够的理论或实验依据。事实上,更简单的经典达西定律能够更精确地刻画低孔隙度介质内的渗流[36-37]。另一方面,对于井中的自由流体而言,考虑到地热发电要求的流量至少为250m3/h[11],对应于井内流动由湍流主导,而Brinkman方程根本无法与湍流模型结合模拟井中湍流。前人虽有基于湍流模型模拟EGS井内湍流的研究[21],但仅限于k-ε模型。由于k-ε模型适用于大雷诺数流动,而EGS井内湍流属于中低雷诺数情形,基于k-ε模型的结果需要通过与其他湍流模型结果对比加以检验。
本文基于多区域多物理场耦合的三维有限元模型,系统研究EGS渗流与传热过程及其对EGS电站寿命的影响。通过连接条件实现不同区域间温度场、压力场和速度场的自然耦合,结合多种湍流模型模拟井内湍流,并探讨以二维模型模拟EGS的条件和有效性。
2 计算模型本文模拟的EGS分成3个区域,即井内区域、渗流储层区域和不可渗透围岩区域。假设储层处于孔隙水饱和状态且没有自然对流发生。模拟中,将井内和储层中的流体流动设为定常的,而整个EGS的温度场是随时间变化的。
井内和储层中的流体速度均满足不可压缩连续性方程
| $ \nabla \cdot \boldsymbol{u}=0. $ | (1) |
不同区域的流动满足不同形式的动量方程。储层中的孔隙流动满足达西定律
| $ \boldsymbol{u}=-\frac{k}{\mu} \nabla_{p}, $ | (2) |
式中:k, μ, p分别为储层渗透率、流体黏度和孔隙压力。井内自由流体的湍流则满足动量方程
| $ \rho(\boldsymbol{u} \cdot \nabla) \boldsymbol{u}=\nabla \cdot\left[-p \boldsymbol{I}+\left(\mu+\mu_{\mathrm{T}}\right)\left(\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right)\right], $ | (3) |
式中:I为单位(恒等)张量,ρ为流体密度,μT为湍流黏度。μT的具体形式由湍流模型定义[33-35, 38-41],而层流对应于μT=0情形。
EGS各区域内满足统一形式的能量方程
| $ \begin{array}{c}{\left[\varphi \rho c_{\mathrm{f}}+(1-\varphi) \rho_{\mathrm{s}} c_{\mathrm{s}}\right] \frac{\partial T}{\partial t}+\rho c_{\mathrm{f}} \boldsymbol{u} \cdot \nabla T-} \\ {\left[\varphi \lambda_{\mathrm{f}}+(1-\varphi) \lambda_{\mathrm{s}}\right] \nabla \cdot \nabla T=0, }\end{array} $ | (4) |
式中:T为温度,t为时间,φ为孔隙度,ρs为固体岩石密度,cf、cs分别为流体和固体比热。通过给定孔隙度取值,方程(4)可以应用于包括井内区域(φ=1)和围岩区域(φ=0)在内的整个EGS计算域。
为实现区域耦合,不同区域的界面上需要满足以下连接条件:1)在注水井、生产井与储层的界面上井内流体压力与储层内孔隙压力连续,井内流体速度与储层内达西速度连续;2)在注水井和生产井与储层的界面上、储层与围岩的界面上温度和热流均连续。
本文模拟的EGS为一个500m×600m×500m的长方体区域。考虑到问题关于y=0的对称性,仅计算y>0一侧即可,如图 1所示。整个计算域包括注水井、生产井、储层与围岩4个区域。采用非结构化四面体网格对计算域进行剖分,共964137个单元,其中井内406075个单元,井中单元最长边0.63m,最短边0.035mm,储层中最长边50m,最短边0.63m。

|
Download:
|
| 图 1 有限元模型及计算域网格剖分 Fig. 1 Finite element model and computational mesh | |
有限元模型参数与物性参数分别由表 1和表 2列出。计算中,在注水井入口指定定常流量(86.8kg/s)的边界条件,而在生产井出口指定压力为零的边界条件。在模拟的EGS储层厚度和地温梯度下,自然对流不会发生[40]。计算中,温度场的瞬态求解取时间步长0.05a。
|
|
表 1 EGS有限元模型参数 Table 1 Parameters of the finite element model for EGS |
|
|
表 2 流体和岩石热物理性质 Table 2 Thermo-physical properties of fluid and rock |
基于SST湍流模型计算得到的三维压力场和流场由图 2给出。图 2(a)和2(b)表明,压力和流体速度主要在水平方向上变化,而在垂向上基本保持不变,呈现出明显的分层流动特征。图 2(c)显示流线跨井壁保持连续。这一结果清楚地表明,通过施加连接条件能够成功实现流场的区域耦合。图 2(d)反映出井周围区域流体速度大,而在离井较远区域流速则较小。两井之间的流线较为密集,形成相对优势流体通道。
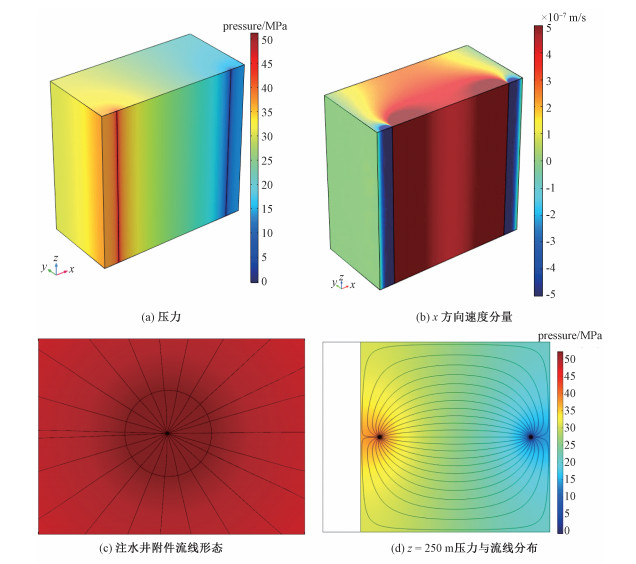
|
Download:
|
| 图 2 三维SST模型压力场与速度场结果 Fig. 2 Results of the 3D SST model for pressure and velocity fields | |
图 3给出基于SST湍流模型计算得到的三维温度场演化,包括EGS工作1、5、10和20a共4个不同时刻的温度截图。图 3显示,由注水井流入的冷水首先冷却注水井周边区域,而后冷却区域逐渐向生产井一侧扩展。温度场在垂向上变化很小,同时在围岩区域热扩散很缓慢,说明传热过程以水平方向热对流主导,而热传导贡献甚微。图 3所示温度场分布的特征还表明,传热的区域耦合也通过施加连接条件得以成功实现。

|
Download:
|
| 图 3 三维SST模型结果:EGS温度场演化 Fig. 3 Results of the 3D SST model: evolution of EGS temperature field | |
不同井内流动三维模型预测的生产井内压力垂向变化与出口温度时间变化由图 4给出。对比的模型包括k-ω,k-ε,小雷诺数k-ε,SST共4种湍流模型和层流模型。图 4(a)表明,4种湍流模型给出的压力变化基本一致,而层流模型预测的井内总压降则只有湍流总压降的约1/4。这一结果清楚地表明井内湍流因受到比层流更高的摩擦阻力而产生更大的压降。然而,不管是不足0.02MPa的井内层流总压降,还是不足0.08MPa的井内湍流总压降,都要比注水井与生产井之间近50MPa的井间总压降(图 2(a))小3个量级。因此,尽管湍流与层流的传热机理和效率有本质上的不同,但就本文模拟的EGS而言,由于井内湍流压降远小于井间渗流压降,导致井内湍流对EGS采热过程的影响不大。图 4(b)表明,除k-ω模型结果略有差异(可能由此模型对入口湍流条件较为敏感所致),几种湍流模型模拟井内流动给出基本一致的生产井出口温度演化,且与层流模型结果很接近。这一结果说明,至少对以水为工质的EGS,在井内湍流效应影响不显著。
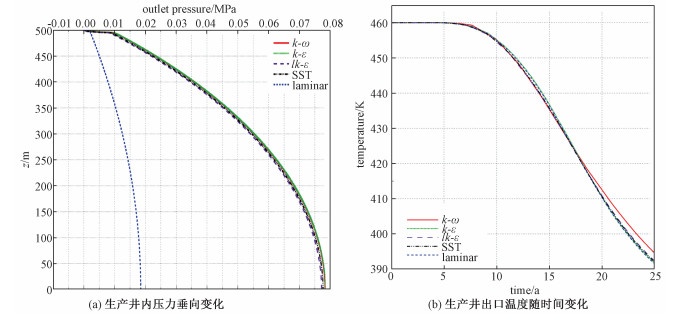
|
Download:
|
| 图 4 不同井内流动三维模型预测结果对比 Fig. 4 Comparison of the predicted results among different 3D models for in-well flows | |
有必要说明的是,本文采用的几种湍流模型均基于雷诺时间平均假设,即没有直接计算湍流对应的速度随时间波动,而是依据特定假设(不同湍流模型采用不同假设)与速度的时间平均值相联系。基于雷诺平均假设的湍流模型不能刻画描述湍流的瞬态细节特征,但用于近似计算湍流压降等的时间平均特征已被大量成功实例所证明是可靠的,事实上也已成为主流工程分析数值模拟软件的“标准配置”。这些相对简单的湍流模型能够满足本文研究的需要,然而要想深入了解多区域、多物理场耦合等情况下的井内湍流的细节,尤其是湍流状态下的传热机理与效率,需要借助更精细的湍流模拟方法,如大涡旋模拟(large eddy simulation, LES)和直接数值模拟(direct numerical simulation,DNS)。LES和DNS需要求解瞬态Navier-Stokes方程,为捕捉湍流涡旋形态还需要保持时间步长足够小,其要求的计算量很大。在EGS数值模拟中,采用LES或DNS以更精确地模拟井内湍流是一个潜在的研究方向。
上述EGS三维数值模拟结果表明,井内湍流因其压降远小于井间渗流压降而对EGS工作状态影响很小。这一发现不但验证了前人在EGS三维数值模拟中直接将井内流动简化为层流的合理性,而且揭示了对适当的EGS问题采用二维模拟的可能性。我们知道,湍流具有三维流动的本质属性,一般情况下是不能简单地用二维模型有效刻画和描述的。然而,在已经清楚了解井内湍流对EGS运行影响可忽略的前提下,如果EGS的结构和物性都没有随深度的变化,而且在储层中没有自然对流发生,则由于井内压降远小于储层内的渗流压降,EGS的流场将以水平流动为特征(图 2)。再考虑到EGS中传热过程由热对流占主导(图 3),则本文模拟的EGS问题可以用二维水平流动和传热模型近似模拟。
从图 1所示三维模型的顶面网格出发,在注水井壁指定注水流量,而在生产井壁给定零压力,我们进行二维有限元模拟。二维模型得到的压力、速度、温度分布(t=20a)与三维模型结果高度一致,如图 5所示。
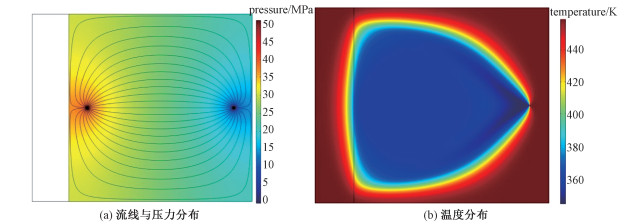
|
Download:
|
| 图 5 二维模型结果 Fig. 5 Results of the 2D model | |
为了更细致地对比二维与三维模拟结果,图 6直接比较二维模型与三维SST模型预测的生产井出口温度曲线。两条曲线总体趋势一致,但存在明显的定量差别。为解释这一差别,我们将二维网格进一步加密,即从自由度18099的2D网格依次增加到自由度357459的细网格(fine)和自由度1415935的极细网格(extremely-fine),并将后两种网格结果一并在图 6中比较。很显然,两种加密网格给出的二维模拟结果在图 6中已经不可区分,表明结果已达到网格无关的精确程度,即有限元离散误差已经小到可以忽略不计的程度,而加密前的二维结果和三维模拟结果则包含不容忽略的离散误差。图 6还清楚地反映出加密前的二维结果比三维结果更接近于网格无关结果,提示加密前的二维结果也比三维结果更精确(因为三维结果还包含在垂直方向上的离散误差)。考虑到三维模拟要求的计算量和计算时间远大于二维模拟,图 6给出的直接对比清楚地显示二维模拟相对于三维模拟在计算精度和效率上具有的巨大优势。
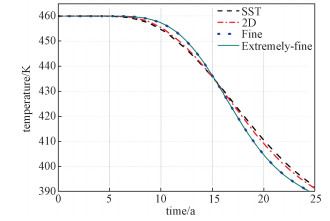
|
Download:
|
| 图 6 三维SST模型预测的生产井温度演化与基于3种网格的两维模型结果对比 Fig. 6 Comparison of production temperature evolution predicted by the 3D SST model with the result predicted by the 2D model employing three meshes | |
基于有限元模型,对一个EGS问题进行三维数值模拟。主要结论如下:1)通过施加正确的连接条件能够实现EGS在不同区域之间的多物理场自然耦合;2)4种湍流模型模拟井内流动给出基本一致的压力变化,井内湍流总压降约为层流模型的4倍,但比注水井与生产井之间的井间总压降小3个量级;3)井内湍流因其压降远小于井间渗流压降而对EGS采热过程总体影响很小,从而在EGS三维数值模拟中可用简单层流模型近似描述井内流动;4)在EGS结构和物性随深度变化、储层中自然对流、井内湍流效应均可忽略的条件下,EGS中流场以水平方向流动为特征,而传热过程由水平方向热对流占主导,因而可以采用二维模型近似模拟。
| [1] |
汪集旸. 加快中国地热发电的步伐[J]. 科技导报, 2012, 30(32): 3. |
| [2] |
Zhang Y, Li Z, Guo L, et al. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells:a case study in Xujiaweizi area in Daqing Oilfield, China[J]. Energy, 2014, 78: 788-805. Doi:10.1016/j.energy.2014.10.073 |
| [3] |
Huang X, Zhu J, Niu C, et al. Heat extraction and power production forecast of a prospective enhanced geothermal system site in Songliao Basin, China[J]. Energy, 2014, 75: 360-370. Doi:10.1016/j.energy.2014.07.085 |
| [4] |
庞忠和, 胡圣标, 汪集旸. 中国地热能发展路线图[J]. 科技导报, 2012, 30(32): 18-24. Doi:10.3981/j.issn.1000-7857.2012.32.001 |
| [5] |
王晓星, 吴能友, 苏正, 等. 增强型地热系统开发技术研究进展[J]. 地球物理学进展, 2012, 27(1): 355-362. |
| [6] |
Huang S. Geothermal energy in China[J]. Nature Climate Change, 2012, 2(8): 557-560. Doi:10.1038/nclimate1598 |
| [7] |
汪集旸, 胡圣标, 庞忠和, 等. 中国大陆干热岩地热资源潜力评估[J]. 科技导报, 2012, 30(32): 25-31. Doi:10.3981/j.issn.1000-7857.2012.32.002 |
| [8] |
Jelacic A, Fortuna R, LaSala R, et al. An evaluation of enhanced geothermal systems technology[R]. Geothermal Technologies Program, US Department of Energy, 2008.
|
| [9] |
许天福, 张延军, 曾昭发, 等. 增强型地热系统(干热岩)开发技术进展[J]. 科技导报, 2012, 30(32): 42-45. Doi:10.3981/j.issn.1000-7857.2012.32.004 |
| [10] |
Llanos E M, Zarrouk S J, Hogarth R A. Numerical model of the Habanero geothermal reservoir, Australia[J]. Geothermics, 2015, 53: 308-319. Doi:10.1016/j.geothermics.2014.07.008 |
| [11] |
李强, 于红侠. 潜山油田地热发电试验工程及应用前景[J]. 煤气与热力, 2012, 32(6): 20-23. Doi:10.3969/j.issn.1000-4416.2012.06.007 |
| [12] |
Gong B, Liang H, Xin S, et al. Numerical studies on power generation from co-produced geothermal resources in oil fields and change in reservoir temperature[J]. Renewable Energy, 2013, 50: 722-731. Doi:10.1016/j.renene.2012.07.026 |
| [13] |
Gong B, Liang H, Xin S, et al. Effect of water injection on reservoir temperature during power generation in oil fields[C]//Proceedings of 36th Workshop on Geothermal Reservoir Engineering. Stanford, California, USA: Uneriversity Stanford, 2011.
|
| [14] |
Bataillé A, Genthon P, Rabinowicz M, et al. Modeling the coupling between free and forced convection in a vertical permeable slot:Implications for the heat production of an enhanced geothermal system[J]. Geothermics, 2006, 35(5): 654-682. |
| [15] |
Blöcher M, Zimmermann G, Moeck I, et al. 3D numerical modeling of hydrothermal processes during the lifetime of a deep geothermal reservoir[J]. Geofluids, 2010, 10(3): 406-421. Doi:10.1111/j.1468-8123.2010.00284.x |
| [16] |
Zhou L, Hou M Z. A new numerical 3D-model for simulation of hydraulic fracturing in consideration of hydro-mechanical coupling effects[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(2): 370-380. |
| [17] |
Jiang F, Luo L, Chen J. A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems[J]. International Communications in Heat and Mass Transfer, 2013, 41: 57-62. Doi:10.1016/j.icheatmasstransfer.2012.11.003 |
| [18] |
Jiang F, Chen J, Huang W, et al. A three-dimensional transient model for EGS subsurface thermo-hydraulic process[J]. Energy, 2014, 72: 300-310. Doi:10.1016/j.energy.2014.05.038 |
| [19] |
Chen J, Jiang F. Designing multi-well layout for enhanced geothermal system to better exploit hot dry rock geothermal energy[J]. Renewable Energy, 2015, 74: 37-48. Doi:10.1016/j.renene.2014.07.056 |
| [20] |
Cao W, Huang W, Jiang F. A novel thermal-hydraulic-mechanical model for the enhanced geothermal system heat extraction[J]. International Journal of Heat and Mass Transfer, 2016, 100: 661-671. Doi:10.1016/j.ijheatmasstransfer.2016.04.078 |
| [21] |
Luo F, Xu R, Jiang P. Numerical investigation of fluid flow and heat transfer in a doublet enhanced geothermal system with CO2 as the working fluid (CO2-EGS)[J]. Energy, 2014, 64: 307-322. Doi:10.1016/j.energy.2013.10.048 |
| [22] |
Li X, Jiang P, Xu R, et al. Experimental investigation on the natural convection heat transfer in the vertical annulus of a CO2 injection well under steady-state conditions[J]. International Journal of Greenhouse Gas Control, 2016, 52: 387-400. Doi:10.1016/j.ijggc.2016.07.011 |
| [23] |
Jiang P, Li X, Xu R, et al. Heat extraction of novel underground well pattern systems for geothermal energy exploitation[J]. Renewable Energy, 2016, 90: 83-94. Doi:10.1016/j.renene.2015.12.062 |
| [24] |
Zeng Y, Su Z, Wu N. Numerical simulation of heat production potential from hot dry rock by water circulating through two horizontal wells at Desert Peak geothermal field[J]. Energy, 2013, 56: 92-107. Doi:10.1016/j.energy.2013.04.055 |
| [25] |
Zeng Y, Wu N, Su Z, et al. Numerical simulation of heat production potential from hot dry rock by water circulating through a novel single vertical fracture at Desert Peak geothermal field[J]. Energy, 2013, 56(63): 268-282. |
| [26] |
Zeng Y, Zhan J, Wu N, et al. Numerical investigation of electricity generation potential from fractured granite reservoir through a single vertical well at Yangbajing geothermal field[J]. Energy, 2016, 114(1): 24-39. |
| [27] |
Pruess K. Enhanced geothermal systems (EGS) using CO2 as working fluid:a novel approach for generating renewable energy with simultaneous sequestration of carbon[J]. Geothermics, 2006, 35(4): 351-367. Doi:10.1016/j.geothermics.2006.08.002 |
| [28] |
Pruess K. On production behavior of enhanced geothermal systems with CO2 as working fluid[J]. Energy Conversion and Management, 2008, 49(6): 1 446-1 454. Doi:10.1016/j.enconman.2007.12.029 |
| [29] |
Saeid S, Al-Khoury R, Barends F. An efficient computational model for deep low-enthalpy geothermal systems[J]. Computers and Geosciences, 2013, 51: 400-409. Doi:10.1016/j.cageo.2012.08.019 |
| [30] |
Saeid S, Al-Khoury R, Nick H, Barends F. Experimental-numerical study of heat flow in deep low-enthalpy geothermal conditions[J]. Renewable Energy, 2014, 62: 716-730. Doi:10.1016/j.renene.2013.08.037 |
| [31] |
Saeid S, Al-Khoury R, Nick H, et al. A prototype design model for deep low-enthalpy hydrothermal systems[J]. Renewable Energy, 2015, 77: 408-422. Doi:10.1016/j.renene.2014.12.018 |
| [32] |
Huang X, Zhu J, Li J. On wellbore heat transfer and fluid flow in the doublet of enhanced geothermal system[J]. Energy Procedia, 2015, 75: 946-955. Doi:10.1016/j.egypro.2015.07.277 |
| [33] |
Wilcox D C. Turbulence model for CFD[M]. California, USA: DCW Industries Inc, 1994.
|
| [34] |
Driver D M, Seegmiller H L. Features of a reattaching turbulent shear layer in divergent channel flow[J]. AIAA Journal, 1985, 23(2): 163-171. Doi:10.2514/3.8890 |
| [35] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1 598-1 605. Doi:10.2514/3.12149 |
| [36] |
Nield D A, Adrian B. Convection in porous media[M]. Berlin: Springer, 2013.
|
| [37] |
Turcotte D L, Schubert G. Geodynamics[M]. Cambridge: Cambridge University Press, 2014.
|
| [38] |
Ignat L, Pelletier D, Ilinca F. A universal formulation of two-equation models for adaptive computation of turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 189(4): 1 119-1 139. Doi:10.1016/S0045-7825(99)00370-9 |
| [39] |
Abe K, Kondoh T, Nagano Y. A new turbulence model for predicting fluid flow and heat transfer in separating and reattaching flows-Ⅰ. Flow field calculations[J]. International Journal of Heat and Mass Transfer, 1994, 37(37): 139-151. |
| [40] |
Lundgren T S. Slow flow through stationary random beds and suspensions of spheres[J]. Journal of Fluid Mechanics, 1972, 51: 273-299. Doi:10.1017/S002211207200120X |
| [41] |
COMSOL. COMSOL multiphysics programming reference mannual[CP]. 2016.
|
 2019, Vol. 36
2019, Vol. 36 


