2. 中国科学院大学, 北京 100049;
3. 中国科学院地理科学与资源研究所, 北京 100101
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
城市建筑物高精度提取对于测绘地理信息、地理国情监测、土地利用调查以及智慧城市、数字城市的建设等领域有着重要的意义。相比于传统的合成孔径雷达(SAR)影像的获取方式,极化合成孔径雷达(PolSAR)可以更加完整地记录目标的后向散射信息,完全表征特定观测频率和姿态下目标的极化散射特性[1],对于建筑物的解译能力更强[2]。随着PolSAR影像数据的极化滤波、目标分解、信息提取等不断的发展与完善,利用PolSAR影像提取建筑物已经成为遥感领域的热点研究内容[3]。
传统的合成孔径雷达影像的建筑物提取多受数据质量、成像原理等因素的制约,PolSAR数据则有效弥补这些不足,在城市建筑物的提取中具有较好应用潜力[4-5]。目前基于PolSAR影像的建筑物提取方法可大致分为3类:基于散射机理、极化统计特征和最优极化的建筑物提取。基于散射机理的建筑物提取通过目标分解将极化测量数据分解成多个表征目标散射或几何结构信息的成分,在一定程度上揭示目标的散射机理;基于极化统计特征的建筑物提取方法的思想是将PolSAR图像中的建筑物作为一类目标,用某种统计模型表征目标及杂波的协方差矩阵或极化散射矢量的统计分布,并基于统计分类方法实现建筑物的提取[6];基于最优极化的建筑物提取则是通过改变发射天线和接收天线的极化状态从而改变目标的回波功率,并通过选择合适的收发天线极化状态提高目标与杂波对比度[7]。PolSAR建筑物提取主要是利用散射机理的方法,使用比较广泛的提取方法主要有Cloude-Pottier分解[8-9]、Freeman-Durden分解[10-11]、Yamaguchi等提出的四分量分解[12]以及张腊梅等提出的MCSM分解[13-14]等方法,但是这些方法存在计算复杂、负功率、体散射估计过高以及极化指向角补偿等问题[15]。An等[16]提出一种改进的Cloude-Pottier分解,可以快速计算H和
由于建筑物的结构、组成成分以及复杂背景等因素的影响,单类的目标散射机理或者某些极化特征并不能很好地描述其散射特性,不同的特征提取方法对其提取效果有较大差异,而且各特征区分建筑物和非建筑物的能力以及建筑物提取的最佳特征组合仍未得到充分的分析和验证。本文选择覆盖苏州市的Radarsat2影像,通过极化非相干分解方法提取出偶次散射等19种极化特征,并基于灰度共生矩阵提取出常规的8种纹理特征,详细分析建筑物、植被和水体这3类典型地物的极化特征,然后基于以上各个特征及特征组合,结合主成分分析法(PCA)和支持向量机法(SVM)[18]进行建筑物的提取,定量分析提取精度,以期为城市建筑提取提供一种更加便捷可靠的方法。
1 实验数据概况研究区位于江苏省苏州市,城市化程度较高。实验数据为Radarsat-2全极化的SLC卫星产品,成像时间为2017年7月17日,采用四极化精细(fine quad polarization)成像模式,空间分辨率为6.17m,景中心经纬度分别是北纬31.3°、东经120.6°,影像实地覆盖范围大小为25km×25km,数据大小为5760像素×3788像素。实验区范围如图 1所示,覆盖苏州市姑苏区、相城区、吴中区等区域,地物类型丰富,包括水体、植被以及建筑物等,中心区域城市建筑物较为集中,四周则较为分散。

|
Download:
|
| 图 1 实验区Radarsat-2影像(2017年7月17日) Fig. 1 Radarsat-2 image of study area | |
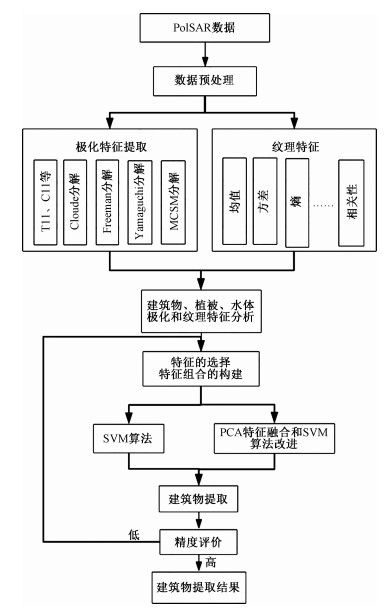
通过极化非相干分解方法提取极化特征,同时提取基于GLCM的纹理特征,对比分析建筑物、植被、水体等3类典型地物的极化和纹理特征,然后进行特征和特征组合的选取和构建,结合SVM分类器提取实验区中的建筑物,最后通过PCA特征融合对建筑物提取算法进行改进。基于极化特征的POLSAR影像的建筑物提取方法流程图 2所示。
|
Download:
|
| 图 2 PolSAR影像建筑物提取方法流程图 Fig. 2 Flow chart of PolSAR building extraction method | |
为了去除SAR影像的相干斑噪声,需要对图像进行滤波。本文选用通用的增强型Lee滤波方法[19]进行相干斑抑制,它是一种基于边缘检测的自适应滤波算法,通过重新定义中心像素的邻域来提高准确性,在降噪的同时也有一定的边缘和纹理保持能力,滤波窗口大小选为5像素×5像素。
2.2 极化特征提取极化协方差矩阵C和相干矩阵T是在极化散射矩阵S的基础上进行二阶统计得到的,包含雷达测量得到的全部极化信息,分别提取两种矩阵的上三角元素作为提取过程中建筑物的特征;极化目标非相干分解方法是将协方差矩阵或相干矩阵分为几种散射机理的加权和,加权系数代表对应的散射机理的强弱,分别用改进的Cloude分解方法、自适应三分量分解和Yamaguchi分解等3种极化分解方法进行极化特征的提取。以上极化特征提取方法及提取的19种极化特征如表 1所示。
|
|
表 1 极化特征提取方法及描述 Table 1 Method and description of polarization feature extraction |
纹理特征是建筑物提取中的又一重要特征,它反映影像的空间分布。目前主要采用灰度共生矩阵(GLCM)统计SAR图像的纹理特征,包括均值、方差、均质性、对比度、相异性、熵、角二阶矩和相关性等。其原理是统计一定窗口内满足某一方向上同一距离的像素对的概率,生成共生矩阵,并在此基础上进行二次统计,最后生成纹理特征,如表 2所示。生成的纹理特征受窗口大小的影响,窗口过大,纹理特征过于模糊,造成边缘损失;窗口太小,提取的纹理特征均质性差,不能很好的反映目标的纹理特征。经实验,本文数据提取纹理特征最适用的窗口大小为5像素×5像素。
|
|
表 2 基于灰度共生矩阵的纹理特征参数 Table 2 Texture feature parameters based on GLCM |
主成分分析[20](principal component analysis,PCA),是通过正交变换将一组可能存在相关性的变量转换为一组线性不相关变量的一种统计方法,转换后的这组变量就是主成分。基于主成分分析的特征融合即是将特征集中的所有特征构成一组变量,然后进行主成分变换,在保证数据信息丢失最少的原则下,用低维变量代替原来的高维变量,从而达到提取主要特征、降低特征间信息冗余的目的。此外,经过PCA特征融合后,原始特征集的维数得到降低,进而提高目标提取算法的效率。该方法的主要流程如下:
1) 对原始数据X进行标准化处理并计算样本的相关系数矩阵R,其中R的大小为p×p。
| $ \boldsymbol{X}=\left[\begin{array}{cccc}{x_{11}} & {x_{12}} & {\cdots} & {x_{1 p}} \\ {x_{21}} & {x_{22}} & {\cdots} & {x_{2 p}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {x_{n 1}} & {x_{n 2}} & {\cdots} & {x_{n p}}\end{array}\right], \boldsymbol{R}=\left[\begin{array}{cccc}{r_{11}} & {r_{12}} & {\cdots} & {r_{1 p}} \\ {r_{21}} & {r_{22}} & {\cdots} & {r_{2 p}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {r_{n 1}} & {r_{n 2}} & {\cdots} & {r_{n p}}\end{array}\right]. $ | (1) |
2) 计算相关系数矩阵R的特征值和特征向量:
特征值
| $ \lambda_{1}, \lambda_{2}, \cdots, \lambda_{P}, $ | (2) |
特征向量
| $ \boldsymbol{\alpha}_{i}=\left(\alpha_{11}, \alpha_{12}, \cdots, \alpha_{1 p}\right), i=1, 2, \cdots, p. $ | (3) |
3) 选择重要的主成分,由主成分分析可以得到P个主成分,从第一主成分至第P个主成分包含的信息量是递减的。实际使用中则会根据情况选择K个主成分。
4) 最后计算得到主成分,形式如下
| $ \begin{aligned} f_{i j}=& \alpha_{j 1} x_{i 1}+\alpha_{j 2} x_{i 2}+\cdots+\alpha_{j p} x_{i p} \\ &(i=1, \cdots, n ; j=1, \cdots, k) \end{aligned}. $ | (4) |
支持向量机(support vector machine, SVM)是建立在统计学习理论的VC维理论和结构风险最小原理基础上的一种机器学习算法,其原理根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷,以期获得最好的推广能力。SVM算法的引入对于高维特征集的建筑物的识别和提取有着重要意义。
2.6 精度评价指标为了更加精确地表征建筑物的提取效果,本文采用精度(Ac)、虚警率(FA)和漏警率(MA)等3个指标进行精度评价,其定义如下:
| $ {{\rm{FA}} = \frac{{{\rm{FP}}}}{{{\rm{TP}} + {\rm{FP}}}}, } $ | (5) |
| $ {{\rm{MA}} = \frac{{{\rm{FN}}}}{{{\rm{TP}} + {\rm{FN}}}}, } $ | (6) |
| $ {{\rm{Ac}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{{\rm{TP}} + {\rm{FN}} + {\rm{FP}} + {\rm{TN}}}}.} $ | (7) |
式中:TP和FP分别为建筑物被正判和错判的像元数;TN和FN分别代表非建筑物被正判和错判的像元数。Ac反映所有被正判的像元比例,MA和FA分别表示建筑物和非建筑物被错判的像元比例。
3 实验结果与分析本文提取实验区Radarsat-2全极化数据的19种极化特征以及8种纹理特征,利用SVM算法(线性核函数)进行建筑物的提取。同时分别选取10000个水体、植被和建筑物的样本点,作为精度评价的基准;并利用这些样本点生成特征散点图,更加直观地表征某一特征对建筑物和非建筑物的可分性。此外,本文分别选取200个建筑物和非建筑物样本点作为SVM算法的训练集,并将其他未分类点作为测试集。
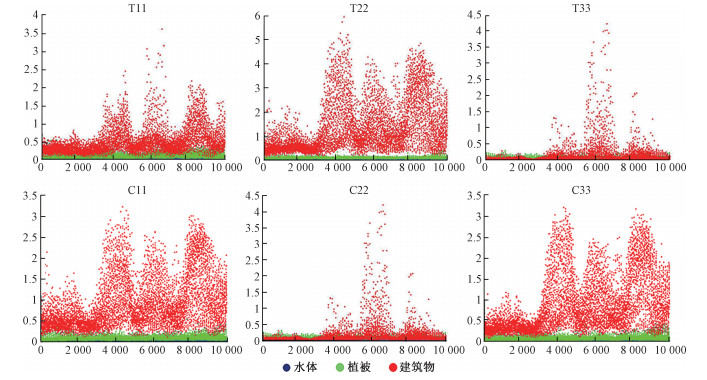
3.1 基于极化特征的建筑物提取结果 3.1.1 基于极化协方差矩阵/相干矩阵建筑物提取结果分别提取极化协方差矩阵和相干矩阵的主对角线元素等6种极化特征,各特征中建筑物、植被和水体的表征以及基于各特征的建筑物提取结果如图 3、图 4和表 3所示。图 4中白色部分为提取的建筑物区域。极化特征T22、C11和C33能很好地区分建筑物和水体,但建筑物和植被之间有一些混淆,造成较高的漏警率,基于以上特征的建筑物提取精度分别是86.2%、86.2%和80%;基于T11的建筑物提取精度为64.4%,该特征能够在一定程度上区分出植被,但误提大部分的水体,导致较高的漏警率和虚警率;在特征T33和C22中3类地物之间存在严重的混淆现象,仅能区分部分具有强后向散射强度的建筑物,因此存在较高的漏警率,建筑物提取精度均为68.5%。
|
Download:
|
| 图 3 极化协方差矩阵/相干矩阵—3类典型地物极化特征图 Fig. 3 Polarization covariance/coherent matrix:polarization signatures of typical ground objects | |

|
Download:
|
| 图 4 极化协方差矩阵/相干矩阵—建筑物提取结果 Fig. 4 Polarization covariance/coherent matrix:building extraction results | |
|
|
表 3 极化协方差矩阵/相干矩阵—建筑物提取结果精度 Table 3 Polarization covariance/coherent matrix:the accuracy of building extraction |
不同的极化特征组合对建筑物的提取效果不同。表 3分别列出建筑物提取效果最佳和最差的几种特征组合。其中,基于所有的6种极化特征的建筑物提取精度为86.0%;建筑物的提取精度最高为87.8%(T22、T33、C11、C22),最低为69.2%(T11、C22)。此外,基于T11、T33、C22和C33间的特征组合精度均在79%以下,而基于其他特征组合的提取精度均大于83%。虽然T22、C11和C33各自的提取精度较高,但特征组合后的提取效果并未得到改善,T22的虚警率较低,有利于降低提取结果的虚警率。
3.1.2 基于改进的Cloude分解的建筑物提取结果由Cloude分解得到了特征值(λ1、λ2和λ3)、散射熵(H)、散射角(

|
Download:
|
| 图 5 改进的Cloude分解—建筑物提取结果及极化特征图 Fig. 5 Building extraction results and polarization signatures of typical ground objects based on advanced Cloude decomposition | |
|
|
表 4 改进的Cloude分解—建筑物提取结果精度 Table 4 Advanced Cloude decomposition:the accuracy of building extraction |
如表 4所示,分别列出建筑物提取最高和最低的几种特征组合,其中,除λ1、H和A之间的组合外,其他所有特征组合对建筑物的提取精度均在80%以上,最高为88.2%(λ1、λ2、
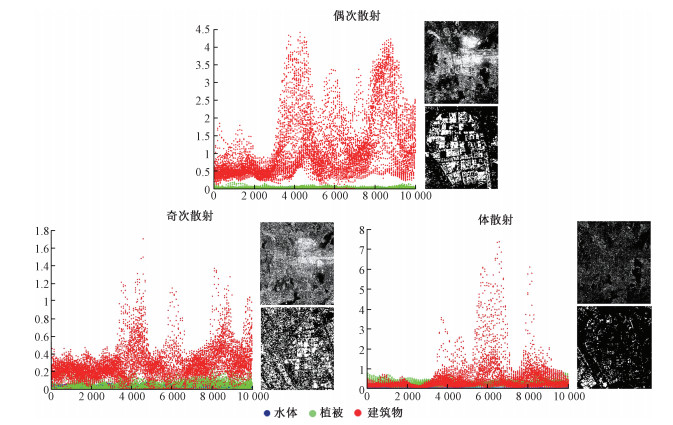
基于自适应三分量分解得到三种极化特征,偶次散射特征、奇次散射特征以及体散射特征。建筑物、植被和水体3类典型地物的极化特征如图 6所示。基于极化特征的建筑物提取精度如表 5所示。其中偶次散射特征几乎可以将建筑物与植被、水体完全区分,基于该特征的建筑物提取精度也最高,可以清晰地提取出建筑物的轮廓和形状;对于奇次散射特征,建筑物与植被混合程度较大,虚警率和漏警率均在46%以上;而体散射特征仅能提取出后向散射系数较高的建筑物,散射系数较低的建筑物与植被完全混淆,因此漏警率很高,但是虚警率较低。
|
Download:
|
| 图 6 自适应三分量分解—建筑物提取结果及极化特征图 Fig. 6 Building extraction results and polarization signatures of typical ground objects based on adaptive three-component decomposition | |
|
|
表 5 基于自适应三分量分解的建筑物提取精度 Table 5 Building extraction precision based on adaptive three-component decomposition |
偶次散射特征与其他特征组合后,建筑物的提取效果反而略有降低,而奇次散射和体散射特征组合后的提取精度仅为67.9%,因此自适应三分量分解中,偶次散射特征对于提取建筑物发挥的作用最大。
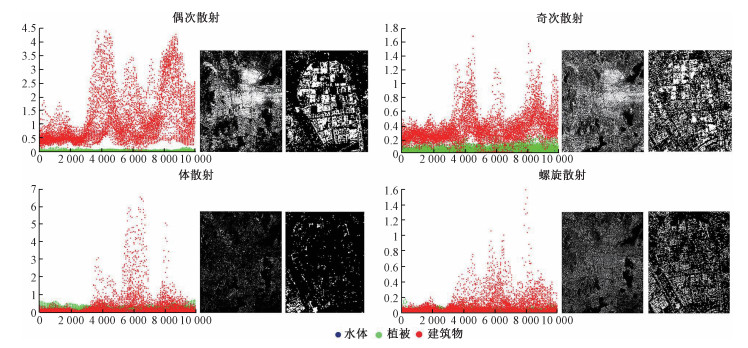
3.1.4 基于Yamaguchi分解的建筑物提取结果由Ymaguchi分解得到4个极化特征,基于各个极化特征的建筑物提取结果以及3类典型地物的极化特征图如图 7所示。其中偶次散射特征可以很好地区分出建筑物,但依然存在漏提现象;奇次散射特征中建筑物和植被有部分混合,提取出建筑物的同时也提取出大量的植被,因此虚警率和漏警率较高,都在40%以上;而体散射和螺旋散射则仅能识别后向散射系数较高的建筑物,因此导致较高的漏警率。
|
Download:
|
| 图 7 Yamaguchi分解—建筑物提取结果及极化特征图 Fig. 7 Building extraction results and polarization signatures of typical ground objects based on Yamaguchi decomposition | |
如表 6所示,在基于不同特征组合的建筑物提取结果中,偶次散射特征其他特征组合后的提取效果较好;基于除偶次散射特征之外的其他特征组合的建筑物提取精度仅为71%左右。因此,Yamaguchi分解中,偶次散射特征对于建筑物提取发挥的作用最大。
|
|
表 6 基于Yamaguchi分解的建筑物提取结果 Table 6 Building extraction precision based on Yamaguchi decomposition |
基于常规的8种纹理特征的建筑物提取结果表 7所示。其中,基于均值的建筑物提取精度最高;其次是方差、对比度和相异性,但在提取建筑物的同时也误提部分植被,因此漏警率和虚警率都较高;对于其他4种纹理特征,建筑物提取效果很差,均质性误提大量的植被,虚警率为51.8%,熵和角二阶矩仅能提取出后向散射系数极强的建筑物,这两种特征的漏警率都超过90%,虚警率都在70%以上;而基于相关性的提取精度虽然低于熵和角二阶矩,但是其漏警率和虚警率都低于二者。
|
|
表 7 基于纹理特征的建筑物提取结果 Table 7 Building extraction results based on texture features |
基于多个纹理特征的建筑物提取精度最高可达87.3%(均值、方差、熵、相关性),其次是87.29%(均值、方差、相关性),87.17%(均值、方差、均质性、角二阶矩、相关性)。基于所有8种纹理特征的建筑物提取精度为87.14%。虽然基于单个纹理特征的提取精度可能高,但通过合适的特征组合可以得到较为理想的提取效果。
3.3 基于特征融合和SVM算法的建筑物提取以上基于单个特征以及特征组合的建筑物提取算法均是在SVM算法基础上进行的,当同时基于多个特征进行分类时,计算复杂度高且效率较低。因此本文首先将提取的极化特征和纹理特征利用PCA算法进行特征降维,并取第一主成分主成分和第二主成分作为新的特征,最后利用SVM算法对PCA变换后的特征进行建筑物提取。其中,PCA特征融合对整体提取算法效率的影响见图 8。可见,PCA特征融合在很大程度上缩短了算法的运行时间,且特征数越多,其效果越明显。

|
Download:
|
| 图 8 PCA特征融合对建筑物提取算法运行时间的影响 Fig. 8 Influence of PCA feature fusion on the algorithm | |
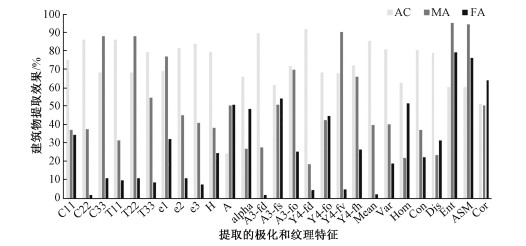
本文将提取到的所有极化特征和纹理特征进行排列组合,基于各特征及特征组合的建筑物提取结果如图 9和表 8、表 9所示。在特征提取方法上,如表 8所示,自适应三分量分解和Yamaguchi分解对建筑物的提取效果最好,原因是偶次散射分量表征着建筑物间常发生的二面角散射,Yamaguchi分解中螺旋散射分量的加入减少了建筑物与植被间的混合,提取精度较高;基于改进的Cloude分解和极化协方差矩阵\相干矩阵的建筑物提取结果中,前者误提了部分植被,后者漏提了部分建筑物;基于纹理特征的提取效果均不如前4种方法。
|
Download:
|
| 图 9 基于各特征的建筑物提取效果 Fig. 9 Building extration accuracy based on each feature | |
|
|
表 8 基于特征提取方法的建筑物提取结果 Table 8 Building extraction results based on feature extraction methods |
|
|
表 9 基于极化特征和纹理特征的建筑物提取结果 Table 9 Building extraction results based on polarization features and texture features |
对于单一特征,如图 9所示,当该特征无法区分建筑物和非建筑,即基于该特征的建筑物提取的虚警率、漏警率都很高,那么该特征组合后则不利于建筑物的提取,如基于灰度共生矩阵的角二阶矩(ASM);当该特征可以区分某一类典型地物,即虚警率或漏警率较低,或者提取精度较高,那么该特征经组合后可能会改善提取效果,例如偶次散射、均值等。
对于特征组合,表 9中前3种为提取效果最好的特征组合,表 10列出分别基于1~27种特征组合中的建筑物提取效果最佳的组合,其中,5种或6种特征融合后建筑物的提取精度最高,虚警率和漏警率都较低。随着特征数的增加,建筑物提取效果反而略有下降,而当特征数增加到27时,提取效果最差,其主要原因可能是有些特征中建筑物和非建筑物混淆严重,扰乱算法的判别过程,例如特征ASM;有些特征则会造成过多的冗余,从而造成精度的下降,例如基于矩阵的极化特征和基于目标分解的极化特征间相关性较大。此外,极化特征与纹理特征组合后,建筑物提取精度得到明显提高,轮廓和边界也更加清晰,而且虚警率和漏警率都有所下降,其中偶次散射分量和均值对于建筑物提取的作用较大。
|
|
表 10 基于特征组合的建筑提取精度 Table 10 Building extraction accuracy based on feature combination |
此外,结合PCA特征融合和SVM的建筑物提取算法在保证提取精度的同时,大大提高整景影像的提取效率,主要原因是主成分分析(PCA)可以选择最有用的特征,从而降低维度,减少特征间的冗余。
4 讨论和分析本文分别采用多种极化非相干分解方法进行特征的提取,并结合纹理特征提取影像中的建筑物,通过特征组合及PCA特征融合后发现,基于Yamaguchi分解的偶次散射、基于自适应三分量分解的偶次散射、基于改进Cloude分解的λ2、以及基于灰度共生矩阵的均值、方差等对建筑物的识别能力较强,同时也可以提高特征组合的提取精度;而基于Yamaguchi分解的螺旋散射、基于自适应三分量分解的奇次散射以及基于灰度共生矩阵的角二阶矩等特征的加入会降低特征组合的提取效果。
由文中的特征散点图和基于各特征组合的建筑物提取结果可以看出,大多数特征中后向散射系数较低的建筑物和植被较易发生混淆,如体散射、螺旋散射、λ1等,这是建筑物提取结果中漏警率大多都较高的原因,同时也一直是PolSAR影像建筑物提取的难点所在。此时利用两类地物纹理特征的不同,与合适的纹理特征结合,如均值、方差等,会在一定程度上降低后向散射系数较低的建筑与植被间的混淆程度,增加分类的可靠性。
利用一些极化特征和纹理特征可以进行水体提取和低后向散射系数的植被(如农田等)提取,例如偶次散射和体散射特征中,水体像元的值基本为零,特征T22中低散射系数的植被可以与建筑物相互区分。
随着PolSAR技术的不断发展,极化特征提取方法的研究和改进层出不穷,对于建筑物提取方面以及其他地物目标提取和分类方面存在着巨大的潜力,同时机器学习、特征融合等算法的快速发展也为建筑物等地物目标提供了更加精确、快速的提取和分类方法。
5 结语1) 特征及特征的选择对于建筑物的提取至关重要,总体来说,基于极化特征的提取精度很大程度上高于基于纹理特征的建筑物提取精度,主要原因是纹理特征仅能表现地物的空间分布特点,极化特征更能充分地利用极化信息描述地物的后向散射特性,从而更好地区分建筑物和非建筑物,而极化特征和纹理特征的结合可以提高建筑物的识别能力。
2) 偶次散射特征对建筑物提取发挥着重要作用,主要原因是偶次散射更能描述建筑物的散射机理,其取值受其他散射分量的影响,同时在该特征中低后向散射系数的建筑物和植被之间较易发生混淆;此外,一些极化特征可用于其他类别地物的识别和提取,而且极化特征和纹理特征在地物的提取和分类上存在着巨大潜力,后续的工作应当针对以上问题再进行更深入的研究。
| [1] |
Zebker H. Polarisation:applications in Remote Sensing[J]. Physics Today, 2010, 63(10): 53-54. |
| [2] |
Lee J S, Pottier E. Polarimetric radar imaging:from basics to applications[M]. London: Chemical Rubber Company Press, 2009: 101-175.
|
| [3] |
张腊梅, 段宝龙, 邹斌. 极化SAR图像目标分解方法的研究进展[J]. 电子与信息学报, 2016, 38(12): 3 289-3 297. |
| [4] |
陈曦, 吴涛, 陶利, 等. 极化SAR发展需求及其目标识别关键技术[J]. 科技视界, 2015(16): 21-22. Doi:10.3969/j.issn.2095-2457.2015.16.014 |
| [5] |
Salehi M, Sahebi M R, Maghsoudi Y. Improving the accuracy of urban land cover classification using Radarsat-2 PolSAR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(4): 1 394-1 401. |
| [6] |
顾钰培, 肖兰玲, 凌婷婷, 等. 一种基于高分辨率遥感影像的建筑物提取方法[J]. 测绘与空间地理信息, 2014(4): 169-171. Doi:10.3969/j.issn.1672-5867.2014.04.049 |
| [7] |
杨杰, 赵伶俐, 史磊, 等. 基于最优极化相干系数的倾斜建筑物解译研究[J]. 测绘学报, 2012, 41(4): 577-583. |
| [8] |
Lee J S, Grunes M R, Ainsworth T L, et al. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier[J]. IEEE Transactions on Geoscience & Remote Sensing, 2002, 37(5): 2 249-2 258. |
| [9] |
Li D, Zhang Y. Random similarity-based entropy/alpha classification of PolSAR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2017, 99: 1-12. |
| [10] |
何连, 秦其明, 任华忠. 一种自适应的混合Freeman/Eigenvalue极化分解模型[J]. 国土资源遥感, 2017, 29(2): 8-14. |
| [11] |
Freeman A, Durden S L. A three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience & Remote Sensing, 1998, 36(3): 963-973. |
| [12] |
Yamaguchi Y, Sato A, Boerner W M, et al. Four-component scattering power decomposition with rotation of coherency matrix[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(6): 2 251-2 258. |
| [13] |
张腊梅.极化SAR图像人造目标特征提取与检测方法研究[D].哈尔滨: 哈尔滨工业大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10213-2011016040.htm
|
| [14] |
Zhang L, Zou B, Cai H, et al. Multiple-component scattering model for polarimetric SAR image decomposition[J]. IEEE Geoscience & Remote Sensing Letters, 2008, 5(4): 603-607. |
| [15] |
Lee J S, Schuler D L, Ainsworth T L. Polarimetric SAR data compensation for terrain azimuth slope variation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2000, 38(5): 2 153-2 163. |
| [16] |
An W, Cui Y, Yang J, et al. Fast alternatives to H/alpha for polarimetric SAR[J]. IEEE Geoscience & Remote Sensing Letters, 2010, 7(2): 343-347. |
| [17] |
蔡永俊, 张祥坤, 姜景山. 极化SAR自适应三分量分解方法[J]. 测绘学报, 2016, 45(9): 1 089-1 095. |
| [18] |
张祥, 邓喀中, 范洪冬, 等. 基于目标分解的极化SAR图像SVM监督分类[J]. 计算机应用研究, 2013, 30(1): 295-298. Doi:10.3969/j.issn.1001-3695.2013.01.076 |
| [19] |
杜培军. RADARSAT图象滤波的研究[J]. 中国矿业大学学报, 2002, 31(2): 25-30. |
| [20] |
Smith L I. A tutorial on principal components analysis[J]. Information Fusion, 2002, 51(3): 52. |
 2019, Vol. 36
2019, Vol. 36 





