在国际热核实验反应堆(international thermonuclear experimental reactor, ITER)中,包层是主要部件之一,它承担着聚变反应所需原料氚的增殖及能量转换双重任务[1]。液态金属在包层流道中流动时,由于受到外部强磁场作用而产生的洛伦兹力将改变速度场分布形式,流场的改变进而影响流体和结构的温度场,也同时引起流道插件热变形和热应力的改变。而在液态双冷锂铅包层(dual coolant lead lithium, DCLL)结构中,流体从入口到出口经历U型流道,即从下到上的入口段,转弯处的过渡段以及转弯后从上到下的出口段,如图 1(a)所示。液态金属流体在这复杂流道内流动会出现不同的三维MHD效应[2-5]。因此对U型流道中的流动、传热及流道插件的力学性能深入研究具有重要的科学意义。
|
Download:
|
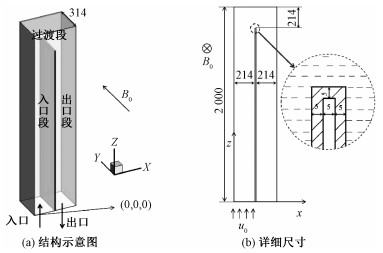
| 图 1 U型流道结构示意图及详细尺寸 Fig. 1 Geometry of the duct and dimensions | |
目前,许多学者[2-8]对于U型流道内的磁流体力学行为进行了研究。Xiao和Kim[2]利用商业软件CFX研究不同横向磁场下矩形导电壁面U型流道中流体的三维MHD效应,结果表明随着磁场强度的增加,入口段和出口段侧壁边界层厚度稍有减小,而侧层处速度峰值有明显提升。Yang和Kim[3]研究固壁电导率对于横向均匀磁场下U型流道流场压降的影响,结果发现流场压降随着固壁电导率的减小而下降。而同一固壁电导率下,不同过渡段长度的U型流道总体压降相同。Chen等[4]研究不同流道插件电导率对均匀磁场下U型流道中流场速度、压力分布的影响,结果显示随着流道插件电导率的变化,流场的速度和压降呈现非线性变化。另外,还发现流道插件的存在大大降低间隙流区流体的速度和压降。Patel[6-7]和Swain等[8]分别采用数值模拟和实验方法研究不同磁场强度下导电的几何复杂通道(包括一段U型管道和两段直角段管道)中的压降分布,结果表明随着磁场的增强,U型管道和两段直角段管道的压降都有显著提升。此外,一些学者对于直通道内的流动特性、传热性能进行了研究,Li等[9]考虑热传递和流固耦合效应研究包层直流道中的温度分布和热位移热应力分布,发现较高的对流换热系数会减少流道插件的温度和热应力,而且不会影响主流区的温度。另外,较低的流道插件热导率能增加主流区的出口温度,但也会增加流道插件的热应力和温度梯度。
由于外部磁场的作用,液态金属流体在U型流道中流动时所产生的诱导电流将改变复杂几何通道内的速度场,速度分布的改变会影响流道内传热性能的变化,特别是在聚变堆中子体积热源的共同作用下,流体和流道结构内会有不同的温度分布,也导致流道插件的变形场和应力场的改变,这在以前研究中涉及较少,有必要进行详细分析。本文采用顺序耦合方法,应用有限体积法和有限元法求解带洛伦兹力源项的Navier-Stokes方程和结构的力平衡方程,模拟U型流道中的速度场、温度场以及流道插件位移场、应力应变场,并研究外加磁场强度、流体进口速度、壁面导电性能对U型流道的流动传热以及流道插件力学性能的影响。
1 问题描述 1.1 计算模型本文的计算模型如图 1所示,该U型流道外侧为厚度为5 mm的流道插件。液态锂铅流体从流道左侧下方流入,右转弯经过渡段后从右侧下方流出,流道截面为214 mm×314 mm,外加磁场与y轴方向相同。此外,假设外侧流道插件全部被氦气包围,其中,氦气温度为673 K,对流换热系数为4 000 W/(m2·K)。表 1列出液态锂铅流体和碳化硅(SiC)流道插件的材料属性。
|
|
表 1 材料属性 Table 1 Material parameters |
在外部横向磁场作用下,金属导电流体流动应满足下列方程:
连续性方程
| $ \nabla \cdot \mathit{\boldsymbol{u}} = 0. $ | (1) |
动量方程
| $ \rho (\mathit{\boldsymbol{u}} \cdot \nabla )\mathit{\boldsymbol{u}} = - \nabla p + \eta {\nabla ^2}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{J}} \times \mathit{\boldsymbol{B}}. $ | (2) |
方程(2)中包含洛伦兹力项J×B。
在磁热流固耦合场中应满足下列方程:
电荷守恒
| $ \nabla \cdot \mathit{\boldsymbol{J}} = 0. $ | (3) |
欧姆定律
| $ \mathit{\boldsymbol{J}} = \sigma ( - \nabla \phi + \mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{B}}). $ | (4) |
能量方程
| $ \rho {C_{\rm{P}}}(\mathit{\boldsymbol{u}} \cdot \nabla T) = k{\nabla ^2}T + \frac{{{\mathit{\boldsymbol{J}}^2}}}{\sigma } + Q. $ | (5) |
式中:u, p, ϕ, J, B, T, ρ, η, σ, CP, k分别为流体速度、压强、电势、电流、磁场强度、温度、密度、动力黏性系数、电导率、定压比热容和热导率,Q为中子热源。Smolentsev等[10]利用中子学计算代码将中子体积热源分布拟合成指数形式,即
| $ Q(x) = 3 \times {10^6} \times {{\rm{e}}^{( - 10x)}}. $ | (6) |
基于静力平衡方程、几何方程、物理关系以及约束条件,采用有限元方法求解流道插件结构的变形和应力,结构中的位移、应力应变满足下列方程:
静力平衡方程
| $ {\sigma _{ij,j}} + {f_i} = 0. $ | (7) |
几何方程
| $ {\varepsilon _{ij}} = \frac{1}{2}\left( {{d_{i,j}} + {d_{j,i}} + {d_{k,i}}{d_{k,j}}} \right) + \alpha \Delta T{\delta _{ij}}. $ | (8) |
本构方程
| $ {\sigma _{ij}} = 2G{\varepsilon _{ij}} + \lambda \theta {\delta _{ij}}. $ | (9) |
式中:di, σij, εij, fi, G, θ, α, δij, λ分别为位移矢量分量、应力张量分量、应变张量分量、外力分量、剪切模量、体积应变、热膨胀系数、克罗内克函数及拉梅系数。
1.3 边界条件在目前的工作中,我们主要研究金属流体流动充分发展后的流动特征和传热特性。在入口处,给定均匀来流速度u0=c,本文选用3种不同的流体进口流速(c=0.878 5, 1.757, 2.635 5 mm/s)研究进口速度对流动、传热的影响。流体入口温度T0=733 K。
在出口处,速度为充分发展边界条件$\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial n}} = 0$,压力p=0。
在流固交界面上速度为无滑移边界条件u=0,温度连续Tsolid=Tfluid,热流连续${k_{{\rm{solid }}}}\frac{{\partial {T_{{\rm{solid }}}}}}{{\partial n}} = {k_{{\rm{fluid }}}}\frac{{\partial {T_{{\rm{funid }}}}}}{{\partial n}}$,电流连续Jsolid·nsolid+Jfluid·nfluid=0。
在流道插件外壁为对流换热边界条件$- k\frac{{\partial T}}{{\partial n}} = h\left( {T - {T_{\rm{f}}}} \right)$,流道插件外壁以及流体域入口、出口壁面绝缘为J=0。
在求解流道插件应力应变时,采用进口处和出口处的位移全约束的方式d=0。
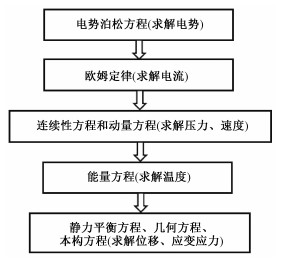
1.4 算法和计算模型验证工作本文基于单向顺序耦合法,结合有限体积法和有限元法研究磁-热-流-固多物理场中的流动传热特性和结构的安全性能。计算流程图如图 2所示。
|
Download:
|
| 图 2 计算流程图 Fig. 2 Flow chart of computational simulation | |
在流场中,将方程(4)代入方程(3)可得到电势泊松方程,即
| $ \nabla \cdot (\sigma \nabla \phi ) = \nabla \cdot (\sigma \mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{B}}). $ | (10) |
先离散电势泊松方程求得电势分布,通过欧姆定律得到电流分布,计算出洛伦兹力后,再利用有限体积法求得U型流道中的压力、速度分布,之后求解能量方程得到流场和结构场中的温度分布。
在流固交界面上采用最小距离标准的搜索算法将流场中的温度传递到流道插件边界上。
流道插件的热应力和热应变采用有限元方法求解,将从流场中得到的温度载荷作为体力载荷加载到流道插件上[9],并用八节点砖块元进行流道插件位移、应力应变求解。温度等效载荷和单元刚度计算如下:
| $ \mathit{\boldsymbol{k}}{\mathit{\boldsymbol{\delta }}^e} = \int\limits_{{V^e}} {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\varepsilon }}_0}{\rm{d}}V,} $ | (11) |
| $ \mathit{\boldsymbol{k}} = \int\limits_{{V^e}} {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}{\rm{d}}V.} $ | (12) |
式中:ε0为温度应变,ε0=αΔT[1 1 1 0 0 0]T,$\int\limits_{{V^e}} {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\varepsilon }}_0}{\rm{d}}V} $为温度等效载荷。k,B,D,δ分别为单元刚度矩阵、单元应变矩阵、弹性矩阵和节点位移列阵。
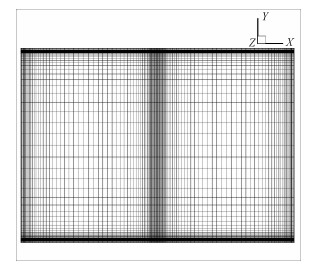
在矩形截面U型通道中,垂直于磁场方向两侧壁面附近边界层为Hartmann层,其厚度约为1/Ha;平行于磁场方向为侧层,其厚度约为$1/\sqrt {Ha} $。在Hartmann层和侧层内电流梯度和速度梯度很大,为保证计算的精确性,对网格的Hartmann层和侧层内需要进行加密,应保证其中有3~5层网格。此外,在U型流道转角附近速度变化剧烈,此处网格也加密以保证速度计算的准确性。网格如图 3所示,磁场沿着Y方向。
|
Download:
|
| 图 3 网格图 Fig. 3 Mesh system | |
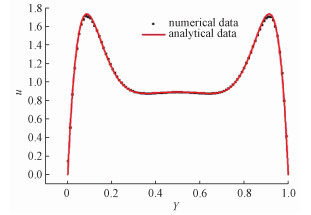
为了验证计算模型,本文通过Hunt模型[11](即在横向磁场下矩形截面流道的充分发展层流模型)对比计算。图 4所示为数值解在侧层及中心区域的速度分布和解析解的对比图。表明本文所采用的计算模型可以准确模拟金属流体在磁场作用下的速度分布,故本文采用相同的计算模型分析U型流道中的速度场和温度场。
|
Download:
|
| 图 4 计算模型验证 Fig. 4 Validation of the computational model | |
本文采用8个算例分析外加磁场强度、进口速度、壁面导电性对U型流道的流动传热的影响。算例所采用参数如表 2所示。其中,前5个算例流道插件绝缘,后3个算例导电。算例1、2、3研究磁场强度对流动、传热的影响,算例3、4、5研究入口速度对流动、传热的影响,算例6、7、8研究流道插件电导率对流动、传热的影响。
|
|
表 2 算例描述 Table 2 Descriptions of the eight cases |
本文引入2个无量纲参数哈特曼数(Hartmann, Ha)和雷诺数(Reynolds number, Re),定义式如下所示:
| $ Ha = {B_0}b\sqrt {\sigma /\mu } . $ | (13) |
| $ Re = \rho {u_0}a/\mu . $ | (14) |
式中:B0, σ, μ, ρ, u0分别为外加磁场强度、金属流体电导率、动力黏性系数、密度和流体进口速度;a, b为特征长度,在本文中分别取流道的半宽和半长,即0.107和0.157 m。要说明的是,case3、4、5这3种不同的进口流速1.757、0.878 5、2.635 5 mm/s对应Re分别为1 000、500、1 500。
2.1.1 典型算例分析U型流道内case1的速度、温度的分布绘制在图 5中。其中,图 5(a)表示case1算例下U型管中y=0.157 m平面内流体速度z方向分量的分布云图。图 5(b)为U型流道在入口段z=1 m平面内y=0.157 m上速度分布,在侧层附近速度变化剧烈,在中心区域分布比较平滑,与Shercliff分布[12]近似。如图 5(a)所示,在入口段靠近过渡段处,靠近内壁(即间隙壁面)的速度较高。涡结构产生在过渡段和出口段连接处附近,此处出现较大的回流速度。在出口段,当接近出口时速度在中心区域分布均匀,同样近似为Shercliff分布。图 5(c)为流线分布图。可以清晰地看出在U型流道出口段靠近间隙壁面以及靠近外壁面有涡结构的存在,而在出口附近流线较为平滑。图 5(d)为温度云图,受到沿x方向呈指数型减小的体积热源以及对流换热边界的影响,高温区域集中在U型流道入口段以及转角处。由于与外界对流换热能力较强,出口处的温度接近于入口处的温度。
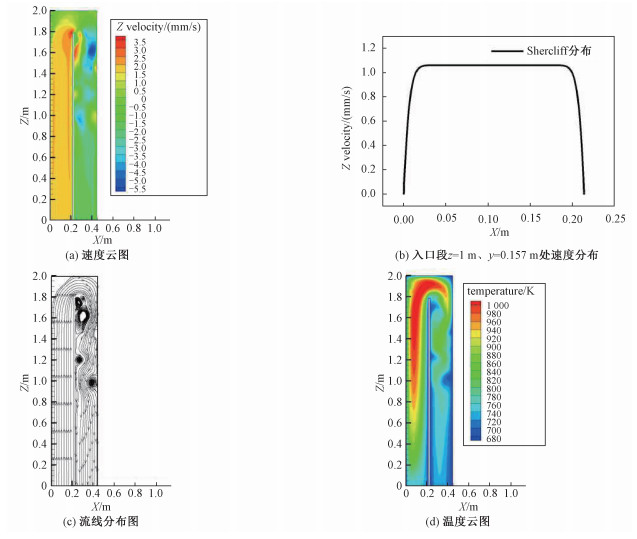
|
Download:
|
| 图 5 Case1算例在y=0.157 m平面内速度、温度分布 Fig. 5 Velocity and temperature at y=0.157 m in case 1 | |
在同一入口速度下(Re=1 000)以及相同流道插件电导率下(σ=0),磁场强度的变化会引起金属流体内诱导电流强度改变,相应洛伦兹力的变化将影响速度场分布和温度场分布。本文以Ha=100,250,500分别研究磁场强度对流动、传热的影响。
图 6绘制y=0.157 m平面内流线分布图以及速度、温度随Ha变化的曲线图。从图 6(a)、6(b)、6(c)可以看出,当Ha为100时,金属流体在转角处出现涡结构。这是因为流体刚转弯流入出口段不能全部充满流道,在转角附近出现负压力梯度,从而有回流产生。此外在出口段z=1.2 m和z=1 m处均有涡结构存在。随着磁场的增强,当Ha为250时,由于洛伦兹力增大,会抑制回流的产生,在出口段z=1 m处涡结构已经消失。当Ha增大到500时,出口段除转角附近涡结构基本消失。图 6(d)对比不同磁场强度下U型流道出口段中心线上的速度。随着磁场强度的增大,中心线上的速度波动越来越小。说明随着Ha的增大,流场趋于稳定。小磁场对流动不稳定有抑制作用。

|
Download:
|
| 图 6 流线分布图和不同Ha下的速度、温度分布 Fig. 6 Velocity streamline and velocity and temperature distributions at different Hartmann numbers | |
图 6(e)、6(f)为温度随Ha变化的曲线图。在z=1 m和z=1.7 m平面内截取位于y=0.157 m处的中心线考察入口段、出口段与过渡段温度分布,其中,曲线图左侧表示U型流道入口段温度分布,右侧为流道出口段温度分布。在z=1 m处,由于入口段速度随着Ha的增大变化微小,入口段温度也基本不发生变化,而出口段温度随着Ha的增大而升高,当Ha超过250时,温度变化很小。在过渡段附近z=1.7 m处,最高温度随着Ha的增大略有提升。
2.1.3 进口速度对流动、传热的影响在同一磁场强度下(Ha=500),本文分别采用Re为500、1 000、1 500这3种情况研究绝缘流道插件内流场和温度场的变化特征,由于流体的流速较低,流动具有层流特性。
流线图以及速度、温度随Re变化的曲线图如图 7所示。其中,纵轴为无量纲速度U(U=uz/u0,u0为入口速度)。图 7(a)、7(b)、7(c)绘制不同入口速度下y=0.157 m平面内流线分布图。当Re为500时,在转角附近有涡结构出现,而出口段其余位置流线大体上均匀分布。当Re达到1 000时,在转角处仍有涡结构存在,但是回流速度更大。这是由于更大的进口速度在转角处产生更大的负压力梯度。当Re增大到1 500时,转角处涡结构数量增多,流线变得混乱。图 7(d)同样说明随着入口速度的增大,流场内速度波动加剧。
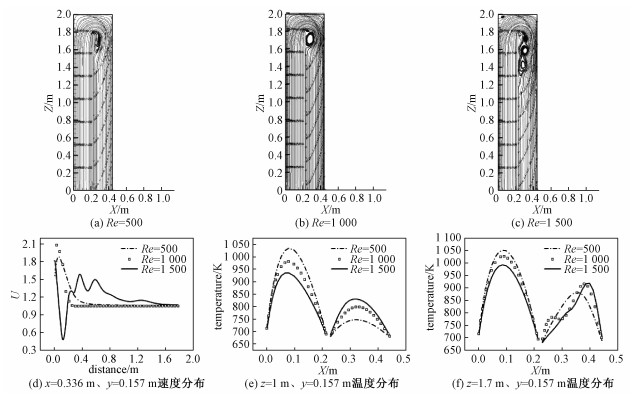
|
Download:
|
| 图 7 流线分布图和不同Re下的速度、温度分布 Fig. 7 Velocity streamline and velocity and temperature distributions at different Reynolds numbers | |
如图 7(e)、7(f)所示,在z=1 m平面内y=0.157 m处,随着入口速度的增大流场吸收的热量减少,入口段温度随Re的增大逐渐降低。而在出口段,温度随Re增大而升高,这是由于较小的流动速度更易受到边界上对流换热性能的影响。在过渡段附近z=1.7 m处,入口段温度随Re的增大而减小,出口段最高温度随Re的增大而有所提升。
2.1.4 流道插件导电率对流动传热的影响为保证隔绝热传递和降低MHD效应,流道插件通常采用SiC材料,当加工工艺不同时,流道插件的电导率有所变化。本文在同一磁场强度下(Ha=500)和同一入口速度下(Re=1 000),讨论电导率对流动、传热的影响。
结构电导率的变化会引起流固耦合场中电势变化,所产生的诱导电流引起的洛伦兹力将改变流体速度分布,继而导致温度场改变。图 8是case6、7、8算例下U型流道中z方向速度、温度分布曲线对比图。如图 8(a)所示,在z=1 m平面内中心线处,当流道插件导电率为100时,流道插件近似绝缘,速度呈现shercliff分布。随着电导率继续增大,流场转变成“M”型分布,即流体域在侧壁处出现极大的速度梯度,且靠近内壁速度峰值比靠近外壁速度峰值高。电导率越大,流体域侧壁峰值也越高。当电导率增大到1 230 000时,速度最大峰值约为入口速度的2.6倍。从图 8(b)可看出,在过渡段附近平面内中心线处,入口段靠近内壁速度同样高于靠近外侧处的速度。在出口段,靠近间隙侧有回流产生,主流区速度随着流道插件导电率增加而减小。
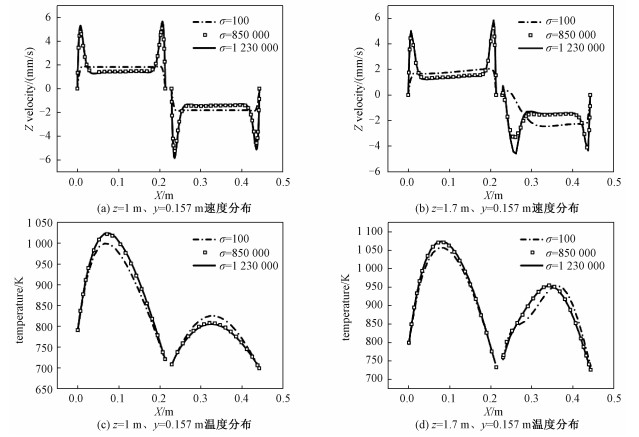
|
Download:
|
| 图 8 不同电导率下的速度、温度分布 Fig. 8 Velocity and temperature distributions at different electrical conductivity values of FCI | |
图 8(c)、8(d)绘制z=1 m和过渡段附近z=1.7 m两处的温度变化曲线图。入口段温度峰值随着电导率的增大而升高,出口段温度峰值随着电导率的增大而降低。随着电导率变化,流道速度分布变化剧烈,但对流换热的影响强于流场速度分布的影响,因此温度只是略有变化。
2.2 U型流道中流道插件的力学分析在这部分对上述8个算例流道插件的力学行为进行有限元分析。将流场中得到的温度传递到结构上,利用式(11)计算出等效温度载荷,再求解流道插件的应变和应力。
流道插件的位移云图、Mises等效应力云图以及应变应力的变化曲线图如图 9所示。其中,图 9(a)为典型的位移云图。由于全约束加载在z=0 m平面内,且高温区域位于U型流道中入口段以及转角处,则在流道插件顶端靠近入口段一侧的位移最大,可达到0.61 mm。从图 9(b)可以看出,流道插件危险区域位于z=0 m约束位置和过渡段侧壁处,但都小于材料许用应力。

|
Download:
|
| 图 9 位移云图、应力云图、应变分布和应力分布 Fig. 9 Displacement contour, stress contour, stress distribution, and strain distribution at z=2.005 m | |
图 9(c)、9(d)、9(e)给出流道插件顶端侧壁附近危险路径上的von Mises应变随磁场、进口速度、电导率变化的曲线图。可以看出,流道插件顶端侧壁的等效应变随磁场的增强而增大;随进口速度的升高而减小;随流道插件电导率的增大略有提升。
图 9(f)、9(g)、9(h)绘制流道插件顶端z=2.005 m平面内y=0.157 m上的von Mises等效应力的变化曲线图。从图 9(f)可以看出,流道插件顶端von Mises等效应力随磁场的增强逐渐升高,这是由于顶端附近温度随着Ha增大而提高,温度场的变化会引起流道插件应力的变化;如图 9(g)所示,当提高进口速度,流道插件等效应力减小。同样受到附近温度场分布的影响,入口速度升高时,金属流体流动过程中单位时间内从热源中吸收的热量减少,U型流道顶端处温度也随之降低,从而热应力也降低;此外,U型流道顶端应力随着流道插件电导率变大而略有提升。虽然电导率的改变,流场分布有很大的变化,但是流道插件在顶端中心线处温度变化不大,从图 9(h)可以看出电导率较大的变化只是略微改变流道插件的应力。
3 结论本文采用有限体积法和有限元法分析U型流道中的速度、温度分布和流道插件中位移、应力分布。研究外加磁场强度、进口速度以及壁面导电性对U型流道内流动、传热和流道插件力学性能的影响。结果显示如下:
1) 磁场强度的变化对于U型流道入口段中的速度和温度影响较小,而对于出口段影响较为明显,出口段流场随磁场强度增强趋于稳定;出口段温度随磁场增强而提升,当Ha超过250时,温度变化不明显;流道插件顶端侧壁的等效应变和应力随磁场增强逐渐增大。
2) 提高入口速度,涡结构随之发生变化,当Re升高到1 500时,出口段流场中出现多个涡结构;出口段最高温度随入口速度增加逐渐升高;侧壁的等效应变和应力则逐渐减小。
3) 当流道插件电导率增大时,流场将呈现“M”型分布,在入口段和出口段,流体域侧壁速度峰值都逐渐提高;而受到边界上对流换热性能的作用,侧壁处温度变化不大;流道插件的应变应力也只是有轻微改变。
4) 高温区域位于入口段与过渡段连接处;最大位移在流道插件过渡段靠近入口段一侧;流道插件应力较大位置在过渡段侧壁附近,但小于插件材料的许用应力。
| [1] |
Rampal G, Li Puma A, Poitevin Y, et al. HCLL TBM for ITER-design studies[J]. Fusion Engineering and Design, 2005, 75-79: 917-922. Doi:10.1016/j.fusengdes.2005.06.322 |
| [2] |
Xiao X J, Kim C N. Magnetohydrodynamic flows in a hairpin duct under a magnetic field applied perpendicular to the plane of flow[J]. Applied Mathematics and Computation, 2014, 240: 1-15. Doi:10.1016/j.amc.2014.04.049 |
| [3] |
Yang S J, Kim C N. Magnetohydrodynamic flows in u-shaped ducts under a uniform transverse magetic field[J]. Fusion Engineering and Design, 2017, 121: 87-99. Doi:10.1016/j.fusengdes.2017.06.007 |
| [4] |
Chen L, Li M J, Ni M J, et al. MHD effects in the U-bend of DCLL blanket[J]. Procedia Engineering, 2015, 126: 461-465. Doi:10.1016/j.proeng.2015.11.272 |
| [5] |
He Q Y, Feng J C, Chen H L. Numerical analysis and optimization of 3D Magnetohydrodynamic flows in rectangular U-bend[J]. Fusion Engineering and Design, 2016, 109-111: 1 313-1 317. Doi:10.1016/j.fusengdes.2015.12.036 |
| [6] |
Patel A, Pulugundla G, Smolentsev S, et al. Validation of numerical solvers for liquid metal flow in a complex geometry in the presence of a strong magnetic field[J]. Theoretical and Computational Fluid Dynamics, 2018, 32: 165-178. Doi:10.1007/s00162-017-0446-9 |
| [7] |
Bhattacharyay R, Patel A, Ellappana R, et al. Liquid metal MHD experimental activities for LLCB TBM development[J]. Fusion Engineering and Design, 2013, 88: 2 244-2 250. Doi:10.1016/j.fusengdes.2013.05.086 |
| [8] |
Swain P K, Satyamurthy P, Bhattacharyay R, et al. 3D MHD lead-lithium liquid metal flow analysis and experiments in a test-section of multiple rectangular bends at moderate to high Hartmann numbers[J]. Fusion Engineering and Design, 2013, 88: 2 848-2 859. Doi:10.1016/j.fusengdes.2013.05.048 |
| [9] |
Li M J, Pan J H, Ni M J, et al. Heat transfer and thermal stress analysis in fluid-structure coupled field[J]. Applied Thermal Engineering, 2015, 88: 473-479. Doi:10.1016/j.applthermaleng.2014.09.071 |
| [10] |
Smolentsev S, Morley N, Abdou M. Magnetohydrodynamic and thermal issues of the SiCf/SiC flow channel insert[J]. Fusion Science and Technology, 2006, 50: 107-119. Doi:10.13182/FST06-A1226 |
| [11] |
Hunt J C R. Magnetohydrodynamic flow in rectangular ducts[J]. Journal of Fluid Mechanics, 1965, 21(4): 577-590. Doi:10.1017/S0022112065000344 |
| [12] |
Shercliff J A. Steady motion of conducting fluids in pipes under transverse magnetic fields[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1953, 49(1): 136-144. Doi:10.1017/S0305004100028139 |
 2019, Vol. 36
2019, Vol. 36 


