2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
外尔(Weyl)半金属[1-2]在提出和发现后,迅速成为研究热点。最近,除已经在实验中观测到的用来体现手征反常的负磁阻效应外[3],实验学家们发现,通过测量外尔半金属的热磁电导,可以证实外尔半金属中存在着引力反常[4]。这无疑给反常理论的研究提供了巨大支持。
外尔半金属是由3+1维的外尔理论来描述的,因此,它是采用2+1维的狄拉克(Dirac)理论所描述的石墨烯的三维类似物。石墨烯在传统凝聚态物理中有着广泛的研究,这些研究大部分集中于弱相互作用下。而理论预言,当石墨烯接近电中性时,可以形成强相互作用的等离子体,即狄拉克流体[5-6]。最近一些实验表明,在石墨烯中确实存在狄拉克流体[7-8],人们可以采用相对论性流体理论方法对相应问题进行研究,例如Lucas等的工作[9-10]。而在外尔半金属中,当费米能靠近外尔点时,在具有反常诱导的输运性质的同时,外尔半金属也会表现出与石墨烯中类似的流体行为,相关流体方法的理论研究见文献[11]。
当系统处于强相互作用时,微扰方法不再适用,除流体方法外,人们还可以通过规范引力对偶(AdS/CFT)对强相互作用进行研究。在AdS/CFT方面,最近构建的一个外尔半金属模型[12]引起广泛关注,基于该模型,人们研究了很多输运性质诸如负磁阻效应[13],奇剪切黏度[14],淬火[15],轴霍尔效应[16],交流电导[17]以及外尔半金属的表面态[18]等。
前面提到的这些效应均为耗散输运,而在带电相对论性流体中,还存在一些非耗散输运现象[19],即在带电相对论性流体中,磁场会诱导出电流,通过手征磁电导反映;此外,流体中的涡旋也会诱导出电流,相应的电导被称为手征涡旋电导,这两种效应被称为手征磁效应和手征涡旋效应。手征磁效应表示磁场通过轴矢量反常诱导电场出现,通过久保公式,文献[20-21]给出它的计算公式,而其现象可以通过负磁阻观测到。
手征涡旋效应[22-23]表示的是流体中一个涡旋会诱导出一个平行于轴旋度矢量的电流[24]。该效应由反常引起,最早由Erdmenger等[22]和Banerjee等[23]通过全息的方法发现。在他们的工作中,计算了在有限化学势下所有流体力学方程中展开到二阶的输运系数(包括线性和非线性)。在一阶微分展开时,他们首次发现存在着一个与流体旋度有关系的输运系数,而这个系数来源于爱因斯坦-麦克斯韦理论中的陈-赛蒙斯(Chern-Simons)项,当陈-赛蒙斯项消失时,此输运系数也不复存在。因此,他们指出该输运系数是由反常引起的,并通过计算发现,该系数正比于化学势的平方以及陈-赛蒙斯项参数。这个系数的发现迅速引起研究热潮,很快Son和Surowka[25]通过流体力学的方法证实了这个系数的存在。他们注意到引入量子三角反常(quantum triangle anomaly)会对流体力学方程的本构关系有重要的修正,不仅会产生剪切黏度,整体黏度以及电导等耗散型的输运系数,还会产生2个新的非耗散输运系数,分别为正比于磁场的手征磁电导和正比于流体旋度的手征涡旋电导。与上述全息方法比较,他们得出在非零化学势下,手征涡旋电导也正比于化学势的平方。Neiman和Oz[26]拓展Son等的工作,考虑了更一般的情况,发现手征涡旋电导在正比于化学势平方的同时,也正比于温度的平方。Landsteiner等通过全息的方法指出,与正比于化学势的平方项来源于手征反常不同,手征涡旋电导中正比于温度平方的项来源于引力反常[19],而在不考虑引力反常时,无法得到温度平方依赖关系[27]。随后,Landsteiner等[28]通过久保公式的方法在弱耦合的情形下证实手征涡旋电导正比于化学势的平方和温度的平方。Jensen等[29]通过平衡态配分函数的计算得到同样的结论。由于在不同方法下人们都得到了相同的结论,因此,手征涡旋效应的存在成为手征反常和引力反常存在的直接证据。考虑到外尔半金属中同时存在着手征反常[3]和引力反常[4],因此,外尔半金属中也应该存在手征涡旋效应。
在本文中,我们在外尔半金属的全息模型中研究手征涡旋效应,计算化学势为零时的手征涡旋电导,发现在引力反常不存在以及温度为零时,手征涡旋效应消失,这与文献[19]的结论一致。而在有限温度时,发现在系统处于外尔半金属相时,手征涡旋效应存在,且手征涡旋电导正比于温度的平方。随着系统逐渐向绝缘体相靠近,该系数缓慢减小。当系统完全变为拓扑平庸的绝缘体相时,手征涡旋电导迅速下降,逐渐趋于零。这充分证明在具有手征费米子的外尔半金属中,引力反常确实存在。
1 外尔半金属全息模型外尔半金属中至少存在着一对外尔点,在外尔点附近的准粒子低能有效激发可以通过左手或右手的外尔旋量来描述。外尔半金属可以通过破坏狄拉克半金属中的时间反演或空间反演对称性得到。考虑在时间反演对称性破坏的情形下,可以在场论中构建外尔半金属模型[30]
| $ L = \bar \Psi \left( {i{\gamma ^\mu }{\partial _\mu } - e{\gamma ^\mu }{A_\mu } - {\gamma _z}{\gamma _5}b + M} \right)\Psi , $ | (1) |
式中:Ψ表示费米场,Ψ=Ψ†γ0,γμ(μ=0, x, y, z)为狄拉克矩阵,具体形式为${{\mathit{\boldsymbol{\gamma}}} ^0} = \left({\begin{array}{*{20}{c}} 0&{{\mathit{\boldsymbol{I}}_2}}\\ {{\mathit{\boldsymbol{I}}_2}}&0 \end{array}} \right); {{\mathit{\boldsymbol{\gamma}}} ^i} = \left({\begin{array}{*{20}{c}} 0&{{\mathit{\boldsymbol{\sigma }}^i}}\\ { - {\mathit{\boldsymbol{\sigma }}^i}}&0 \end{array}} \right), i = x, y, z, {\mathit{\boldsymbol{\sigma }}^i}$为泡利矩阵,I2为2×2的单位矩阵。有关系式${\mathit{\boldsymbol{\gamma }}_\mu } = {\mathit{\boldsymbol{\eta }}_{\mu \nu }}{\mathit{\boldsymbol{\gamma }}^\nu }, {\mathit{\boldsymbol{\eta }}_{\mu \nu }}$为平坦时空度规矩阵,其对角元为(1, -1, -1, -1),其他元为零,γ5=iγ0γxγyγz,Aμ表示相应的U(1)规范场,b和M为2个自由参数。在模型(1)中,随着b和M的不同取值,该模型所描述的系统可以实现从拓扑非平庸的外尔半金属相到拓扑平庸的绝缘体之间的相变。
模型(1)建立在准粒子描述成立的情形,即系统处于弱相互作用时的理论。而当系统处于强相互作用时,准粒子的概念不再适用,此时有必要构建一个模型,以使其能够在强相互作用下满足外尔半金属的性质,同时还要呈现出模型(1)所经历的相变。AdS/CFT在相关问题上具有巨大的优势,根据规范引力对偶词典[31](gauge/gravity dual dictionary),可以构建全息形式下的外尔半金属的模型[12]:
| $ \begin{array}{l} S = \int {{{\rm{d}}^5}} x\sqrt { - g} \left[ {(R + 12) - \frac{1}{4}{F^2} - \frac{1}{4}F_5^2 + } \right.\\ \;\;\;\;\;\;\frac{\alpha }{3}{\varepsilon ^{\mu \nu \rho \sigma \tau }}{A_\mu }\left( {3{F_{\nu \rho }}{F_{\sigma \tau }} + {F_{5\nu \rho }}{F_{5\sigma \tau }}} \right) - V(\mathit{\Phi }) - \\ \;\;\;\;\;\;\left. {{{\left( {{D_\mu }\mathit{\Phi }} \right)}^*}\left( {{D^\mu }\mathit{\Phi }} \right)} \right]. \end{array} $ | (2) |
式中:(R+12)部分来源于爱因斯坦引力;F和F5表示2个规范场(矢量型场Vμ以及轴矢量场Aμ),分别对应电磁场的U(1)对称性以及轴矢量的U(1)对称性,相应的场强分别为Fμν=∂μVν-∂νVμ,F5μν=∂μAν-∂νAμ;F5表征手征反常,具体可以通过陈-赛蒙斯项以及外加标量场Φ的质量项来体现;α为陈-赛蒙斯项的耦合强度;εμνρστ为李维-赛维塔张量(Livi-Civita tensor);标量场Φ只在轴规范变换下携带规范荷,相应的协变导数定义可以通过轴矢量场Aμ定义为${D_\mu }\mathit{\Phi} = \left({{\partial _\mu } - } \right.\left. {{\rm{i}}q{A_\mu }} \right)\mathit{\Phi} $,为简便起见,可以将q取为1。标量场的质量项在势能$V(\mathit{\Phi}) = {m^2}{\mathit{\Phi} ^2} + \frac{\lambda }{2}{\mathit{\Phi} ^4}$中。在模型(2)中要求物质场A和Φ满足边界条件$\mathop {\lim }\limits_{r \to \infty } {A_z}(r) = b$以及$\mathop {\lim }\limits_{r \to \infty } \varphi (r) = M$,可以引入场论模型(1)中的自由参数。在模型(2)中通过全息方法计算反常霍尔电导,可以发现M/b≈0.7为临界点,当M/b < 0.7时,系统处于外尔半金属相,而当M/b>0.7时,系统处于拓扑平庸的绝缘体相,此结论与通过模型(1)计算的结果一致[12]。
模型(2)中只体现了手征反常,而当需要考虑引力反常时,需要在陈-赛蒙斯项中增加表示引力反常的项,具体为εμνρστAμζRδνρβRβστδ,其中Rδνρβ为黎曼张量,ζ代表引力反常耦合强度。引力反常会引起奇剪切黏度[14](odd viscosity)以及手征涡旋效应,下一小节,将研究手征涡旋效应在外尔半金属中的具体行为。
2 外尔半金属中的手征涡旋效应对于手征涡旋电导,可以通过久保公式[19]来计算
| $ \sigma _A^{{\rm{CVE}}} = \mathop {\lim }\limits_{{p_c} \to 0} \frac{i}{{2{p_c}}}\sum\limits_{a,b} {{\varepsilon _{abc}}} {\left\langle {J_A^a{T^{0b}}} \right\rangle _R},(\omega = 0,\mathit{\boldsymbol{p}}), $ | (3) |
即需要计算推迟流流关联函数(retard current-current correlation function),即〈JAaT0b〉R。
在有限温度情形下考虑如下度规假设${\rm{d}}{s^2} = - u{\rm{d}}{t^2} + \frac{{{\rm{d}}{r^2}}}{u} + f\left({{\rm{d}}{x^2} + {\rm{d}}{y^2}} \right) + h{\rm{d}}{z^2}$, 并且假设$A = {A_z}{\rm{d}}z, \mathit{\Phi} = \phi $,在这种假设下,化学势为零。其中,u, f, h, Az, ϕ都为r的实场。可以通过作用量对度规和场求变分得到背景运动方程,具体如下:
| $ \begin{array}{*{20}{l}} {{u^{\prime \prime }} + \frac{{{h^\prime }}}{{2h}}{u^\prime } - \left( {{f^{\prime \prime }} + \frac{{{f^\prime }}}{{2h}}{h^\prime }} \right)\frac{u}{f} = 0,}\\ \begin{array}{l} \left( {{m^2} + \frac{\lambda }{2}{\phi ^2} - \frac{{{q^2}A_z^2}}{h}} \right) - \frac{{A_z^\prime }}{{4h}} + \frac{{{\phi ^{\prime 2}}}}{2} = 0,\\ \begin{array}{*{20}{l}} {\frac{{{\phi ^{\prime 2}}}}{2} + \frac{6}{u} - \frac{{{u^\prime }}}{{2u}}\left( {\frac{{{f^\prime }}}{f} + \frac{{{h^\prime }}}{{2h}}} \right) - \frac{{{f^\prime }}}{{2fh}}{h^\prime } - \frac{{{f^{\prime 2}}}}{{4{f^2}}} + }\\ \begin{array}{l} \frac{{{A^{2\prime }}z}}{{4h}} - \frac{{{\phi ^2}}}{{2u}}\left( {{m^2} + \frac{\lambda }{2}{\phi ^2} + \frac{{{q^2}A_z^2}}{h}} \right) = 0,\\ \begin{array}{*{20}{l}} {A_z^{\prime \prime } + \left( {\frac{{{f^\prime }}}{f} - \frac{{{h^\prime }}}{{2h}} + \frac{{{u^\prime }}}{u}} \right)A_z^\prime - \frac{{2{q^2}{\phi ^2}}}{u}{A_z} = 0,}\\ {{\phi ^{\prime \prime }} + \left( {\frac{{{f^\prime }}}{f} + \frac{{{h^\prime }}}{{2h}} + \frac{{{u^\prime }}}{u}} \right){\phi ^\prime } - }\\ {\left( {{m^2} + \lambda {\phi ^2} + \frac{{{q^2}A_z^2}}{h}} \right)\frac{\phi }{u} = 0.} \end{array} \end{array} \end{array} \end{array} \end{array} $ | (4) |
这些方程都是二阶微分方程,需要假设2个边界条件。这2个边界条件分别加在视界r=r0处以及AdS边界处r→∞。在这2个位置,可以对场进行渐进展开。通常处理中,要求场在视界处是正规的,因此,度规场u, f, h和物质场Az, ϕ在视界处的展开形式为:
| $ u = 4{\rm{ \mathsf{ π} }}T\left( {r - {r_0}} \right) + \cdots , $ |
| $ f = {f_1} + {C_1}\left( {r - {r_0}} \right) + \cdots , $ |
| $ h = {h_1} + \cdots , $ |
| $ {A_z} = {A_{z1}} + {A_{z2}}\left( {r - {r_0}} \right) + \cdots , $ |
| $ r\phi = {\phi _1} + {C_2}\left( {r - {r_0}} \right) + \cdots , $ |
| $ {C_1} = - {f_1}{A_{z2}}\frac{{2\phi _1^2{m^2}r_0^2 - 24r_0^4 + \lambda \phi _1^4}}{{6{A_{z1}}\phi _1^2{q^2}r_0^2}}, $ |
| $ {C_2} = \frac{{\frac{{{A_{z2}}{r_0}}}{{{A_{z1}}}}\left( {\frac{{A_{z1}^2}}{{{h_1}}} + \frac{{{m^2}}}{{{q^2}}}} \right) + \phi _1^2\left( {\frac{2}{{{r_0}}} + \frac{{{A_{z2}}\lambda }}{{{A_{z1}}{q^2}}}} \right)}}{{2{\phi _1}}}, $ |
其中温度$T = \frac{{{A_{z1}}\varphi _1^2{q^2}}}{{2\pi r_0^2{A_{z2}}}}$。在视界处,自由参量为T, r0, f1, h1, Az1, Az2, ϕ1。考虑到标度对称性,这些自由参量将减少到2个,在对偶场论中,这2个参量为无量纲参数M/b, T/b。
当把视界处的解进行积分直到无穷远处(AdS边界处)时,可以得到场在边界处的渐进展开行为,具体如下
| $ u = {r^2} - \frac{{{M^2}}}{3} + \frac{{{M^4}(2 + 3\lambda )}}{{18}}\frac{{\ln r}}{{{r^2}}} - \frac{{{M_b}}}{{3{r^2}}} + \cdots , $ |
| $ f = {r^2} - \frac{{{M^2}}}{3} + \frac{{{M^4}(2 + 3\lambda )}}{{18}}\frac{{\ln r}}{{{r^2}}} + \frac{{{f_3}}}{{3{r^2}}} + \cdots , $ |
| $ h = {r^2} - \frac{{{M^2}}}{3} + {C_3}\frac{{\ln r}}{{{r^2}}} + \frac{{{h_3}}}{{{r^2}}} + \cdots , $ |
| $ {A_z} = b - b{M^2}{q^2}\frac{{\ln r}}{{{r^2}}} + \frac{\xi }{{{r^2}}} + \cdots , $ |
| $ r\phi = M - {C_4}\frac{{\ln r}}{{6{r^2}}} + \frac{O}{{{r^2}}} + \cdots , $ |
| $ {C_3} = \frac{{{M^4}(2 + 3\lambda )}}{{18}} + \frac{{{q^2}{b^2}{M^2}}}{2}, $ |
| $ {C_4} = 2{M^3} + 3{b^2}M{q^2} + 3\lambda {M^3}. $ |
以上场的运动方程及渐进行为都是在没有任何扰动情形下的背景解。在全息中,推迟流流关联函数可以通过对背景加扰动来实现,即将扰动当成源S,此时扰动对系统产生的作用称之为响应R,根据线性响应理论,可以得到关系R=GS,其中G代表相应的流流关联函数(格林函数)。
考虑到手征涡旋电导的计算公式,需要打开动量方向的扰动。具体来说,可以打开z方向的微扰进行计算,形式如下:
| $ \begin{array}{*{20}{l}} {\delta {g_{xz}} = {h_{xz}}(r){{\rm{e}}^{{\rm{i}}kz}},\delta {g_{xz}} = {h_{xz}}(r){{\rm{e}}^{{\rm{i}}kz}},}\\ {\delta {g_{tx}} = {h_{tx}}(r){{\rm{e}}^{{\rm{i}}kz}},\delta {g_{ty}} = {h_{ty}}(r){{\rm{e}}^{{\rm{i}}kz}},}\\ {\delta {A_x} = {a_x}(r){{\rm{e}}^{{\rm{i}}kz}},\delta {A_y} = {a_y}(r){{\rm{e}}^{{\rm{i}}kz}}.} \end{array} $ | (5) |
将上述微扰(5)代入背景运动方程中,可以得到相应的线性运动方程
| $ h_{ti}^{\prime \prime } + \frac{{{h^\prime }}}{{2h}}h_{ti}^\prime + {D_1}{h_{ti}} + \frac{{2i\zeta k}}{{\sqrt h }}\left[ {\frac{{A_z^\prime }}{h}\left( {{u^\prime } - \frac{{u{f^\prime }}}{f}} \right)h_{jz}^\prime - \frac{{A_z^\prime {f^\prime }}}{{fh}}\left( {{u^\prime } - \frac{{u{f^\prime }}}{f}} \right){h_{jz}} + {E_1}a_j^\prime + {F_1}{a_j}} \right] = 0, $ |
| $ h_{iz}^{\prime \prime } + \left( {\frac{{{u^\prime }}}{u} - \frac{{{h^\prime }}}{{2h}}} \right)h_{iz}^\prime + \left( {\frac{{{f^\prime }}}{{2fh}}{h^\prime } - \frac{f}{{2h}}{u^\prime } - \frac{{{f^{\prime \prime }}}}{f}} \right){h_{iz}} + A_z^\prime a_i^\prime + \frac{{2{q^2}{\mathit{\Phi }^2}{A_z}}}{u}{a_i} + \frac{{2i\zeta k}}{{\sqrt h }}\left[ {A_z^\prime \left( {\frac{{{u^\prime }}}{u} - \frac{{{f^\prime }}}{f}} \right)h_{tj}^\prime + {G_1}{h_{tj}}} \right] = 0, $ |
| $ a_i^{\prime \prime } + \left( {\frac{{{u^\prime }}}{u} + \frac{{{h^\prime }}}{{2h}}} \right)a_i^\prime - \left( {\frac{{2{q^2}{\mathit{\Phi }^2}{A_z}}}{u} + \frac{{k_z^2}}{{hu}}} \right){a_i} - \frac{{A_z^\prime }}{h}h_{iz}^\prime + \frac{{A_z^\prime }}{h}h_{iz}^\prime + \frac{{A_z^\prime }}{{fh}}{f^\prime }{h_{iz}} + \frac{{2i\zeta k}}{{\sqrt h }}\left( {{H_1}h_{tj}^\prime + {P_1}{h_{tj}}} \right) = 0. $ |
其中i, j=x, y,在运动方程中出现的系数D1, E1, F1, G1, H1, P1都为u, f, h及其高阶导数的函数。除这6个二阶微分方程外,还有2个与上述微分方程自洽的一阶微分方程,在这里不做考虑。
在有限温度时,可以将上述微扰按小量k展开。即
| $ \begin{array}{*{20}{l}} {{h_{ti}} = {h_{ti(0)}} + k{h_{ti(1)}} + {k^2}{h_{ti(2)}} + \cdots ,}\\ {{h_{iz}} = {h_{iz(0)}} + k{h_{iz(1)}} + {k^2}{h_{iz(2)}} + \cdots ,}\\ {{a_i} = {a_{i(0)}} + k{a_{i(1)}} + {k^2}{a_{i(2)}} + \cdots .} \end{array} $ | (6) |
其中,hti, hiz, ai在视界处均满足正规条件。
可以将式(6)代入到微扰的线性运动方程中逐阶求解。在零阶k时,有方程
| $ \begin{array}{l} \begin{array}{*{20}{c}} {h_{ti(0)}^{\prime \prime } + \frac{{{h^\prime }}}{{2h}}h_{t(0)}^\prime - \left( {\frac{{{f^{\prime \prime }}}}{f} + \frac{{{f^\prime }{h^\prime }}}{{2fh}}} \right){h_{t(0)}} = 0}\\ {h_{iz(0)}^{\prime \prime } + \left( {\frac{{{u^\prime }}}{u} - \frac{{{h^\prime }}}{{2h}}} \right)h_{iz(0)}^\prime + \left( {\frac{{{f^\prime }{h^\prime }}}{{2fh}} - \frac{{{f^{\prime \prime }}}}{f} - } \right.} \end{array}\\ \begin{array}{*{20}{c}} {\left. {\frac{{{f^\prime }{u^\prime }}}{{fu}}} \right){h_{iz(0)}} + A_z^\prime a_{(0)}^\prime + \frac{{2{q^2}{\Phi ^2}{A_z}}}{u}{a_{(0)}} = 0}\\ {a_{i(0)}^{\prime \prime } + \left( {\frac{{{u^\prime }}}{u} + \frac{{{h^\prime }}}{{2h}}} \right)a_{i(0)}^\prime - \frac{{2{q^2}{\Phi ^2}}}{u}a_{i(0)}^\prime - }\\ {\frac{{A_z^\prime }}{h}h_{iz(0)}^\prime + \frac{{{A^\prime }{f^\prime }}}{{fh}}{h_{iz(0)}} = 0} \end{array} \end{array} $ | (7) |
根据运动方程结合方程(7),可以得到ht(0)=u。对于aj(0)和hjz(0), 为简便起见,可以选取合适的边界条件,使得这2个系数满足hjz(0)=0, aj(0)=0, j=x, y。
在上述解的基础上,可以得到k的一阶方程,为方便求解,我们做了变换Hiz=hizf。以x方向为例,相应的方程为
| $ h_{tx(1)}^{\prime \prime } + \frac{{{h^\prime }}}{{2h}}h_{tx(1)}^\prime - \left( {\frac{{{f^{\prime \prime }}}}{f} + \frac{{{f^\prime }{h^\prime }}}{{2fh}}} \right){h_{tx(1)}} = 0, $ |
| $ \begin{array}{*{20}{l}} {H_{xz(1)}^{\prime \prime } + \left( {\frac{{{u^\prime }}}{u} - \frac{{{h^\prime }}}{{2h}} + \frac{{{f^\prime }}}{{2f}}} \right)H_{xz(1)}^\prime + \frac{{A_z^\prime }}{f}a_{x(1)}^\prime + }\\ {\frac{{2{q^2}{\mathit{\Phi }^2}{A_z}}}{{fu}}{a_{x(1)}} + \frac{{2i\zeta }}{{f\sqrt h }}\left[ {A_z^\prime \left( {\frac{{{u^\prime }}}{u} - \frac{{{f^\prime }}}{f}} \right){u^\prime } + {G_1}u} \right] = 0.} \end{array} $ |
从上式中的第1个方程可以给出
| $ \frac{{u{f^2}}}{{\sqrt h }}H_{xz(1)}^\prime = - A_z^\prime \frac{{uf}}{{\sqrt h }}{a_{x(1)}} - 2i\zeta A_z^\prime \left( {\frac{{{u^\prime }}}{u} - \frac{{{f^\prime }}}{f}} \right)\frac{{{u^2}f}}{h}, $ |
基于此,ax(1)的方程为
| $ \begin{array}{*{20}{c}} {a_{x(1)}^{\prime \prime } + \left( {\frac{{{u^\prime }}}{u} + \frac{{{h^\prime }}}{{2h}}} \right)a_{x(1)}^\prime - \left( {\frac{{2{q^2}{\mathit{\Phi }^2}}}{u} - \frac{{A_z^{\prime 2}}}{h}} \right){a_{x(1)}} + }\\ {\frac{{2i\zeta }}{{f\sqrt h }}\left( {\frac{{{u^\prime }}}{u} - \frac{{{f^\prime }}}{f}} \right){L_1} = 0,}\\ {{L_1} = \frac{{2{q^2}{\mathit{\Phi }^2}A_z^2}}{h} + \frac{{2u}}{h}A_z^{\prime 2} + u\left( {\frac{{{h^\prime }}}{h} - \frac{{{u^\prime }}}{u}} \right)\left( {\frac{{2{f^\prime }}}{f} + \frac{{{h^\prime }}}{h}} \right).} \end{array} $ | (8) |
从方程(8)中可以得到如下极限情形:1)当ζ=0时,方程变为齐次方程,表明ax(1)是无源的,即没有相应的线性响应,此时手征涡旋效应消失。如前所述,ζ代表引力反常,因此,可以得出结论,手征涡旋效应的确可以由引力反常引起;2)当u=f时,从度规的假设来看,此时系统处于高度对称性,对应于零温的情形,此时方程仍然变为齐次方程,这与文献[19]中手征涡旋电导与温度平方成正比相符合。
3 数值结果接下来,将通过方程(8)的数值求解得到手征涡旋电导的表达式。首先,给出涨落在AdS时空边界的渐进行为
| $ \begin{array}{l} {h_u} = h_{ui}^{(0)}{r^2} - h_u^{(0)}\left( {\frac{{{k^2}}}{4} + \frac{{{M^2}}}{3}} \right) + \frac{{\ln r}}{{{r^2}}}\frac{{{h_{t(0)}}}}{{144}}\left( {9{k^2} + } \right.\\ \;\;\;\;\;\;\;\left. {16{M^4} + 24\lambda {M^4} + 6{M^2}{k^2}} \right) + \frac{{h_u^{(2)}}}{{4{r^2}}} + \cdots , \end{array} $ |
| $ \begin{array}{l} {h_{iz}} = h_{iz}^{(0)}{r^2} - h_{iz}^{(0)}\frac{{{M^2}}}{3} + \frac{{\ln r}}{{{r^2}}}\left[ {\frac{{h_{iz}^{(0)}}}{{18}}\left( {2{M^4} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {\left. {3{M^4}\lambda } \right) + 2a_i^{(0)}b{M^2}{q^2}} \right] + \frac{{h_{iz}^{(2)}}}{{4{r^2}}} + \cdots , \end{array} $ |
| $ {a_i} = a_i^{(0)} - a_i^{(0)}\left( {{M^2}{q^2} + \frac{{{k^2}}}{2}} \right)\frac{{\ln r}}{{{r^2}}} + \frac{{a_i^{(2)}}}{{{r^2}}} + \cdots . $ |
根据R=GS以及手征涡旋电导计算公式,可以得知,手征涡旋电导是在源hti下的ai的响应。而源为hti在AdS时空边界的渐进行为中r2的系数hti(0),而响应为ai在AdS时空边界的渐进行为中1 /r2的系数ai(2),为此,需要将涨落行为代入到在壳作用量(on-shell action)[14],并取至微扰的二阶小量,根据GKPW规则[31],可以得到手征涡旋电导的数值解。在数值计算中,令ζ=1。
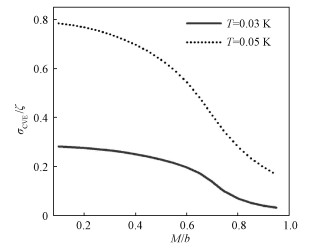
如图 1所示,计算在不同温度时,手征涡旋电导随外部参数M/b变化的情形。从图中可以看出,手征涡旋电导随温度的增加而增加,在系统处于外尔半金属相(M/b < 0.7)时,手征涡旋电导随M/b缓慢减小,这表明在外尔半金属中,由引力反常诱导的手征涡旋效应的确存在;而当系统处于拓扑平庸的绝缘体相(M/b>0.7)时,手征涡旋电导迅速下降并趋向于0,这正是在拓扑平庸的绝缘体中手征外尔费米子消失的体现。
|
Download:
|
| 图 1 不同温度下手征涡旋电导随参数M/b的变化 Fig. 1 Variation in chiral vortical conductivity with M/b at T=0.03 K (solid line) and T=0.05 K (dotted line) | |
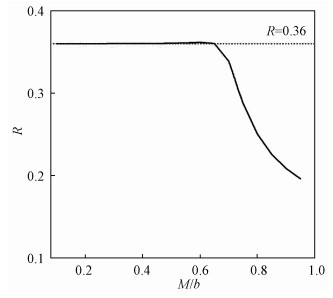
为进一步验证手征涡旋电导对温度的依赖关系,我们计算了$R = \frac{{\sigma _{{\rm{CVE}}}^{T = 0.03}}}{{\sigma _{{\rm{CVE}}}^{T = 0.05}}}$随外部参数M/b变化的情形,如图 2所示。可以从图中清晰地看出,当系统处于外尔半金属相时,R的值为0.36(恰好等于2个不同温度的平方的比值0.032/0.052,在图 2中用水平点线表示),而当系统处于拓扑平庸的绝缘体相时,R逐渐趋近于0。这充分表明,在外尔半金属中,由引力反常诱导的手征涡旋效应的确存在,且与温度平方成正比,而在绝缘体相时,手征涡旋电导很快消失。
|
Download:
|
| 图 2 R随参数M/b的变化图 Fig. 2 Variation in R with M/b | |
本文通过规范/引力对偶的方法研究强耦合下外尔半金属中的手征涡旋效应。在考虑系统只有引力反常的情形下,得到如下结论:1)手征涡旋效应可以由引力反常引起,在具有手征费米子的外尔半金属中存在;2)手征涡旋效应与温度有密切关系,与温度平方成正比,在零温时,手征涡旋效应消失。
| [1] |
Wan X G, Turner A M, Vishwanath A, et al. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates[J]. Physical Review B, 2011, 83(20): 205 101. Doi:10.1103/PhysRevB.83.205101 |
| [2] |
Weng H M, Fang C, Fang Z, et al. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides[J]. Physical Review X, 2015, 5(1): 011 029. Doi:10.1103/PhysRevX.5.011029 |
| [3] |
Son D T, Yamamoto N. Berry curvature, triangle anomalies, and the chiral magnetic effect in Fermi liquids[J]. Physical Review Letter, 2012, 109(18): 181 602. Doi:10.1103/PhysRevLett.109.181602 |
| [4] |
Gooth J, Niemann A C, Meng T, et al. Experimental signatures of the mixed axial-gravitational anomaly in the Weyl semimetal NbP[J]. Nature, 2017, 547: 324-327. Doi:10.1038/nature23005 |
| [5] |
Müller M, Sachdev S. Collective cyclotron motion of the relativistic plasma in graphene[J]. Physical Review B, 2008, 78(11): 115 419. Doi:10.1103/PhysRevB.78.115419 |
| [6] |
Müller M, Fritz L, Sachdev S. Quantum-critical relativistic magnetotransport in graphene[J]. Physical Review B, 2008, 78(11): 115 406. Doi:10.1103/PhysRevB.78.115406 |
| [7] |
Crossno J, Shi J K, Wang K, et al. Observation of the Dirac fluid and the breakdown of the Wiedemann-Franz law in graphene[J]. Science, 2016, 351: 1 058-1 061. Doi:10.1126/science.aad0343 |
| [8] |
Ghahari F, Xie H Y, Taniguch T, et al. Enhanced thermoelectric power in graphene:violation of the Mott relation by Inelastic scattering[J]. Physical Review Letter, 2016, 116(13): 136 802. Doi:10.1103/PhysRevLett.116.136802 |
| [9] |
Lucas A, Crossno J, Fong K C, et al. Transport in inhomogeneous quantum critical fluids and in the Dirac fluid in graphene[J]. Physical Review B, 2016, 93(7): 075 426. Doi:10.1103/PhysRevB.93.075426 |
| [10] |
Lucas A. Sound waves and resonances in electron-hole plasma[J]. Physical Review B, 2016, 93(24): 245 153. Doi:10.1103/PhysRevB.93.245153 |
| [11] |
Lucas A, Davison R A, Sachdev S. Hydrodynamic theory of thermoelectric transport and negative magnetoresistance in Weyl semimetals[J]. Proceedings of the National Academy of Sciences, 2016, 113(34): 9 463-9 468. Doi:10.1073/pnas.1608881113 |
| [12] |
Landsteiner K, Liu Y. The holographic Weyl semi-metal[J]. Physics Letters B, 2016, 753: 453-457. Doi:10.1016/j.physletb.2015.12.052 |
| [13] |
Sun Y W, Yang Q. Negative magnetoresistivity in holography[J]. Journal of High Energy Physics, 2016, 1609: 122. |
| [14] |
Landsteiner K, Liu Y, Sun Y W. Odd viscosity in the quantum critical region of a holographic Weyl semimetal[J]. Physical Review Letter, 2016, 117(8): 081 604. Doi:10.1103/PhysRevLett.117.081604 |
| [15] |
Ammon M, Grieninger S, Jimenez-Alba A, et al. Holographic quenches and anomalous transport[J]. Journal of High Energy Physics, 2016, 1609: 131. |
| [16] |
Copetti C, Fernández-Pendás J, Landsteiner K. Axial Hall effect and universality of holographic Weyl semimetals[J]. Journal of High Energy Physics, 2017, 1702: 138. |
| [17] |
Grignani G, Marini A, Pena-Benitez F, et al. AC conductivity for a holographic Weyl semimetal[J]. Journal of High Energy Physics, 2017, 1703: 125. |
| [18] |
Ammon M, Heinrich M, Jiménez-Alba A, et al. Surface States in Holographic Weyl Semimetals[J]. Physical Review Letter, 2017, 118(20): 201 601. Doi:10.1103/PhysRevLett.118.201601 |
| [19] |
Landsteiner K, Megias E, Melgar L, et al. Holographic gravitational anomaly and chiral vortical effect[J]. Journal of High Energy Physics, 2011, 1109: 121. |
| [20] |
Kharzeev D E, Warringa H J. Chiral magnetic conductivity[J]. Physical Review D, 2009, 80(3): 034 028. Doi:10.1103/PhysRevD.80.034028 |
| [21] |
Hou D, Liu H, Ren H C. Some field theoretic issues regarding the chiral magnetic effect[J]. Journal of High Energy Physics, 2011, 1105: 046. |
| [22] |
Erdmenger J, Haack M, Kaminski M, et al. Fluid dynamics of R-charged black holes[J]. Journal of High Energy Physics, 2009, 0901: 055. |
| [23] |
Banerjee N, Bhattacharya J, Bhattacharyya S, et al. Hydrodynamics from charged black branes[J]. Journal of High Energy Physics, 2011, 1101: 094. |
| [24] |
Kharzeev D E, Warringa H J. Cancellation of equilibrium parity-violating currents[J]. Physical Review D, 1980, 22(12): 3 067. Doi:10.1103/PhysRevD.22.3067 |
| [25] |
Son D T, Surowka P. Hydrodynamics with triangle anomalies[J]. Physical Review Letter, 2009, 103(19): 191 601. Doi:10.1103/PhysRevLett.103.191601 |
| [26] |
Neiman Y, Oz Y. Relativistic hydrodynamics with general anomalous charges[J]. Journal of High Energy Physics, 2011, 1103: 023. |
| [27] |
Amado I, Landsteiner K, Pena-Benitez F. Anomalous ransport coefficients from Kubo formulas in Holography[J]. Journal of High Energy Physics, 2011, 1105: 081. |
| [28] |
Landsteiner K, Megias E, Pena-Benitez F. Gravitational anomaly and transport phenomena[J]. Physical Review Letter, 2011, 107(02): 021 601. Doi:10.1103/PhysRevLett.107.021601 |
| [29] |
Jensen K, Kaminski M, Kovtun P, et al. Towards hydrodynamics without an entropy current[J]. Physical Review Letter, 2012, 109(10): 101 601. Doi:10.1103/PhysRevLett.109.101601 |
| [30] |
Colladay D, Kostelecky V A. Lorentz-violating extension of the standard model[J]. Physical Review D, 1998, 58(11): 116 002. Doi:10.1103/PhysRevD.58.116002 |
| [31] |
Gubser S S, Klebanov I R, Polyakov A M. Gauge theory correlators from noncritical string theory[J]. Physics Letters B, 1998, 428: 105. Doi:10.1016/S0370-2693(98)00377-3 |
 2019, Vol. 36
2019, Vol. 36 


