近年来,狄拉克费米子以其独特的电子性质引起广泛关注。以石墨烯为例,在其布里渊区顶点(K, K’)处能带相交,色散呈现线性关系,形成2个不等价的狄拉克费米子,分别携带(π,-π)的Berry Phase[1-2].在自旋轨道耦合作用下,能带的简并点处会打开能隙,从而形成拓扑绝缘体相[3]。与之相似的情形也存在于三维材料中,如Bi2Se3, Bi2Te3这类具有较大自旋-轨道耦合的材料,在打开能隙的同时会引发能带的翻转,从而形成拓扑绝缘体[4-5]。
判断材料是否为拓扑绝缘体主要有3种方法。一种是根据体态-边缘态对应原则,通过手性边缘态或表面态是否存在来判定是普通绝缘体还是拓扑绝缘体;一种是通过绝热地改变参数,在不闭合能隙的情况下将材料转化为某一拓扑性质已知的结构来进行分类;最后一种也是最常用的一种方法就是计算相应的拓扑不变量来进行判断。对于量子霍尔效应或陈绝缘体,其拓扑不变量为陈数(TKNN数)[6]。对于拓扑绝缘体,其拓扑不变量为Z2数[7-8]。目前已经有成熟的数值方法可以方便地计算这类拓扑数[9-11]。
对于某些由于对称性而导致的特殊能带结构,比如镜面对称性和滑移对称性同时存在,会引起能带沿高对称线简并,一般的数值方法由于出现发散而失效。在SS格子上运动的电子便是一个典型例子。SS格子在量子磁性系统中已经被广泛研究[12-13],相应结构的材料SrCu2(BO3)2也已经被发现。然而,SS格子上的费米子系统还需进一步探索。此前有研究通过调节紧束缚模型的参数,指出SS格子上运动的电子可以呈现出Dirac fermion, semi-Dirac fermion, SO(3) fermion和quadratic band touch等4种无能隙激发的物相以及一个有能隙的相[14-15]。然而,需要有一种便捷的调控手段实现对紧束缚模型参数的调控。
在许多调控手段中,光场无疑是一种方便且可靠的调控技术。以石墨烯为例,如果在垂直于石墨烯表面的方向施加周期性光场,可以实现狄拉克点的移位[16-17],打开动力学能隙实现拓扑转变[18-20],产生偏振选择性的光伏霍尔效应[21],甚至引发金属-绝缘体相变[22]。更一般地,周期性光场可以将一般的绝缘体变成Floquet拓扑绝缘体[23-24],在某些条件下,可以形成具有大陈数的Floquet-陈绝缘体[25]。光场不仅可以准静态地改变能带结构,还能形成新的动力学拓扑效应[26-27],如Floquet手征边缘态等[16, 27-28]。
本文应用周期性圆偏振光场调控SS格子上的电子结构,可以很方便地产生前面提到的5种相。有研究指出Dirac fermion相具有Z2形式的量子化Zak相[14],在自旋-轨道耦合的作用下会形成拓扑绝缘体。我们通过计算纳米带的边缘态,证明在自旋轨道耦合存在的情况下,光场调控可以视为绝热地改变参数,不会导致能隙关闭,从而使其他4种相与Dirac fermion相具有相同的拓扑性质。同时还发现semi-Dirac fermion相的一种体态-边缘态对应情况。
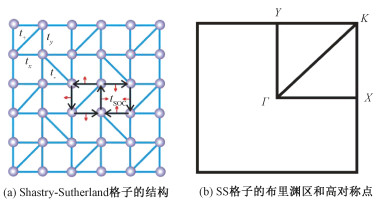
1 Shastry-Sutherland格子的结构和紧束缚哈密顿量SS格子的结构如图 1所示,其中tx, ty, t+, t-为跃迁参数,tsoc为自旋轨道耦合参数。黑色箭头表示电子跃迁方向,橘红色箭头表示电子受力方向。具有1个四重旋转轴,1个滑移面和1个反演中心。这些对称性导致SS格子具有特殊的能带结构。
|
Download:
|
| 图 1 SS格子的实空间和倒空间结构 Fig. 1 Structure of Shastry-Sutherland lattice (a) and its reciprocal space(b) | |
因为一个SS格子的元胞中有4个原子,所以s轨道紧束缚哈密顿量是一个四带模型
| $ {\mathit{\boldsymbol{H}}_k} = {\left( {{\mathit{\boldsymbol{H}}_k}} \right)_{ij}}c_{ki}^\dagger {c_{kj}}. $ |
i, j遍及格点1~4,如图 1中所示。我们将跃迁参数定义为tx, ty, t+, t-,这样紧束缚哈密顿量可以写为
| $ {\mathit{\boldsymbol{H}}_k} = \left( {\begin{array}{*{20}{c}} 0&{2{t_x}\cos {k_x}a}&{2{t_y}\cos {k_y}a}&{{t_ + }\exp \left( {{\rm{i}}a\left( {{k_x} - {k_y}} \right)} \right)}\\ {2{t_x}\cos {k_x}a}&0&{{t_{\rm{i}}}\exp \left( {{\rm{i}}a\left( {{k_x} + {k_y}} \right)} \right)}&{2{t_y}\cos {k_y}a}\\ {2{t_y}\cos {k_y}a}&{{t_ - }\exp \left( { - {\rm{i}}a\left( {{k_x} + {k_y}} \right)} \right)}&0&{2{t_x}\cos {k_x}a}\\ {{t_ + }\exp \left( { - {\rm{i}}a\left( {{k_x} - {k_y}} \right)} \right)}&{2{t_y}\cos {k_y}a}&{2{t_x}\cos {k_x}a}&0 \end{array}} \right). $ | (1) |
由于SS格子沿着x方向和y方向不存在镜面对称性,故电子以动量P在沿着这2个方向跃迁时,会受到不对称的作用力F,根据自旋-轨道耦合作用公式
| $ {\mathit{\boldsymbol{H}}_{{\rm{so}}}} = \frac{h}{{4m_0^2{c^2}}}(\mathit{\boldsymbol{F}} \times \mathit{\boldsymbol{P}}) \cdot \mathit{\boldsymbol{\sigma }}, $ |
可以看出受力与自旋z分量耦合,当电子环绕晶格一圈时,虽然平均受力为0,但是自旋轨道耦合方向相同,不会抵消。在考虑自旋轨道耦合作用tsoc之后的紧束缚哈密顿量为
| $ {\mathit{\boldsymbol{H}}_k} = \left( {\begin{array}{*{20}{c}} 0&{2\left( {{t_x} - {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_x}a}&{2\left( {{t_y} + {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_y}a}&{{t_ + }\exp \left( {{\rm{i}}a\left( {{k_x} - {k_y}} \right)} \right)}\\ {2\left( {{t_x} + {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_x}a}&0&{{t_ - }\exp \left( {{\rm{i}}a\left( {{k_x} + {k_y}} \right)} \right)}&{2\left( {{t_y} - {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_y}a}\\ {2\left( {{t_y} - {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_y}a}&{{t_ - }\exp \left( { - {\rm{i}}a\left( {{k_x} + {k_y}} \right)} \right)}&0&{2\left( {{t_x} + {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_x}a}\\ {{t_ + }\exp \left( { - {\rm{i}}a\left( {{k_x} - {k_y}} \right)} \right)}&{2\left( {{t_y} + {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_y}a}&{2\left( {{t_x} - {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos {k_x}a}&0 \end{array}} \right). $ | (2) |
以此紧束缚哈密顿量为基础,可以得到存在周期性光场时的Floquet哈密顿量。
2 Floquet-Bloch理论现在考虑垂直入射的周期性光场调控下的SS格子系统。周期性光场调控下的哈密顿量同样也应该是周期性的,即H(t+T)=H(t), T是光场的周期。类似于空间周期平移不变系统中的布洛赫定理,同样也可以写出在周期光场下的波函数满足的条件:
| $ \begin{array}{*{20}{l}} {\mathit{\Psi }(t) = \exp ( - {\rm{i}}\varepsilon t)\mathit{\Phi }(t),}\\ {\mathit{\Phi }(t + T) = \mathit{\Phi }(t).} \end{array} $ | (3) |
这就是Floquet定理[29-30],其中Φ(t)是Floquet波函数。
同样可以定义Flouqet哈密顿量
| $ H_k^F(t) = {H_k}(t) - {\rm{i}}{\partial _t}, $ | (4) |
容易发现ε和Φ就是Floquet哈密顿量的本征值和本征函数。当体系具有时间-空间周期平移不变性,波函数遵循Floquet-Bloch定理
| $ \mathit{\Psi }(x,t) = \exp \left( {{\rm{i}}kx - {\rm{i}}{\varepsilon _{n,k}}t} \right)\mathit{\Phi }(x,t). $ |
在这种情况下,可以重新定义时间平均的内积
| $ \left\langle \left\langle {{\mathit{\Phi }_n}(t)|{\mathit{\Phi }_m}(t)} \right\rangle = \frac{1}{T}\int_0^T {\left\langle {{\mathit{\Phi }_n}(t)|{\mathit{\Phi }_m}(t)} \right\rangle } {\rm{d}}t \right.. $ | (5) |
这一新的定义保证了Floquet-Bloch波函数的基底满足正交归一性。为证明这一点,需要注意Floquet哈密顿量和Floquet波函数都可以做傅里叶级数展开:
| $ {\mathit{\Phi }_\alpha }(t) = \sum\nolimits_n {\exp ({\rm{i}}n\omega t){\mathit{\Phi }_{\alpha ,n}}} $ |
将傅里叶级数代入内积公式中有
| $ \begin{array}{*{20}{l}} {\left\langle {\left\langle {{\mathit{\Phi }_\alpha }(t)|{\mathit{\Phi }_\beta }(t)} \right\rangle } \right\rangle }\\ { = \sum\limits_{m,n} {\frac{1}{T}} \int_0^T {\left\langle {{\mathit{\Phi }_{\alpha ,n}}|{\mathit{\Phi }_{\beta ,m}}} \right\rangle } \exp ({\rm{i}}(m - n)\omega t){\rm{d}}t}\\ { = \sum\limits_{m,n} {{\delta _{\alpha ,\beta }}} {\delta _{m,n}} = {\delta _{\alpha ,\beta }}} \end{array} $ | (6) |
将希尔伯特空间推广到时间域中做展开的空间,被称为Sambe空间[31]。
光场的作用可以通过Peierls替换进入紧束缚模型的跃迁参数,ti, j(t)=ti, jexp(iA(t)dij),其中i, j是格点指标,dij是i, j格点之间的跃迁矢量,A=(Ax, Ay)是光场对应的矢量势。在Sambe空间中展开Floquet紧束缚哈密顿量可以得到矩阵元:
| $ \begin{array}{l} {H_{ij}} = \left\langle {\left\langle {{\Phi _i}\left| {H - {\rm{i}}{\partial _t}} \right|{\Phi _j}} \right\rangle } \right\rangle \\ \;\;\;\;\; = \sum\limits_{m,n} {\frac{1}{T}} \int_0^T {\langle {\mathit{\Phi }_{i,n}}\left| {H(t)\exp ({\rm{i}}(m - n)t) - } \right.} \\ \;\;\;\;\;{\rm{i}}m\omega {\delta _{m,n}}\left| {{\Phi _{j,m}}} \right\rangle \\ \;\;\;\;\; = \sum\limits_{m,n} {{H_{mn,ij}}} - m\omega I, \end{array} $ |
| $ \begin{array}{l} {H_{nm,ij}} = \frac{1}{T}\int_0^T {\sum\limits_{{{\vec d}_{i,j}}} {{t_{i,j}}} } \exp \left( {{\rm{i}}(\mathit{\boldsymbol{k}} + \mathit{\boldsymbol{A}}(t)) \cdot {\mathit{\boldsymbol{d}}_{i,j}}} \right)\exp ({\rm{i}}(m\\ \;\;\;\;\;\;\;\;\; - n)\omega t). \end{array} $ | (7) |
由于时间平移不变性,Hmn是p=(m-n)的函数,重新定义为Hp.那么,在Sambe空间中的哈密顿量可以写为
| $ {\mathit{\boldsymbol{H}}^F} = \left[ {\begin{array}{*{20}{c}} \ddots & \vdots & \vdots & \vdots &{}\\ \cdots &{{H_0} - w}&{{H_1}}&{{H_2}}& \cdots \\ \cdots &{{H_{ - 1}}}&{{H_0}}&{{H_1}}& \cdots \\ \cdots &{{H_{ - 2}}}&{{H_{ - 1}}}&{{H_0} + w}& \cdots \\ {}& \vdots & \vdots & \vdots & \ddots \end{array}} \right] $ |
当光场频率远大于能带宽度(ω>10Δ),可以忽略更高阶Hp的影响而只需要计算H0即可,这被称为高频近似。在高频近似下,取tx=ty=t1, t+=t-=t2, 光场为圆偏振光,SS格子的Floquet哈密顿量可以写为
| $ \begin{array}{l} \mathit{\boldsymbol{H}} = \left( {\begin{array}{*{20}{c}} 0&{{H_a}}&{{H_b}}&{{H_c}}\\ {H_a^*}&0&{{H_d}}&{{H_b}}\\ {H_b^*}&{H_d^*}&0&{{H_a}}\\ {H_c^*}&{H_b^*}&{H_a^*}&0 \end{array}} \right),\\ \begin{array}{*{20}{l}} {{H_a} = 2\left( {{t_1} - {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos \left( {{k_x}a} \right){{\rm{J}}_0}\left( {a{A_x}} \right),}\\ \begin{array}{l} {H_b} = 2\left( {{t_1} + {\rm{i}}{t_{{\rm{soc}}}}} \right)\cos \left( {{k_y}a} \right){{\rm{J}}_0}\left( {a{A_y}} \right),\\ \begin{array}{*{20}{l}} {{H_c} = {t_2}\exp \left( {{\rm{i}}a\left( {{k_x} - {k_y}} \right)} \right){{\rm{J}}_0}(a\sqrt {A_x^2 + A_y^2} ),}\\ {{H_d} = {t_2}\exp \left( { - {\rm{i}}a\left( {{k_x} + {k_y}} \right)} \right){{\rm{J}}_0}(a\sqrt {A_x^2 + A_y^2} ).} \end{array} \end{array} \end{array} \end{array} $ | (8) |
其中J0为0阶贝塞尔函数。
基于式(8),我们计算了导带电子在没有自旋轨道耦合作用下的相图[32],相图中一共存在5种相:能隙相,以及Dirac fermion, semi-Dirac fermion, SO(3) fermion和quadratic band touch等4种无能隙相。Dirac fermion和能隙相由2种边界区分开,其中一种为semi-Dirac fermion相,另外一种为quadratic band touch相。在2种边界的交汇点处出现的是SO(3) fermion相,被4条semi-Dirac fermion边界包围在中间的是能隙相。换言之,一共有3种无能隙激发存在于边界处:能带以semi-Dirac形式接触存在于能隙相和Dirac相之间,能带以quadratic形式接触存在于2个Dirac相之间,能带以SO(3) fermion形式接触存在semi-Dirac和quadratic band touch汇合的顶角处。
在4种无能隙的激发中,Dirac fermion占据绝大多数的情况。在光场调控下,2条能带以线性方式交叉于狄拉克点处,2个狄拉克点关于原点中心对称,在光场的调控下,狄拉克点不再固定于布里渊区的高对称点处,而是被光场在一定范围内移动并发生位置交换[14]。高频近似下,Floquet哈密顿量保持时间反演和空间反演对称性,使得Dirac fermion被对称性所保护,这一点在考虑了自旋轨道耦合之后将变得更为明显。
Quadratic band touch是另一个值得注意的无能隙激发,它的标志就是2条抛物线色散关系的能带相交于一点。由于SS格子具有C4旋转对称性,所以这种无能隙激发携带有2π的Berry phase[32]。在一般情形下,圆偏振光会破坏时间反演对称性,引入能隙形成拓扑非平庸的电子态[33],但是在SS格子中,第一阶高频展开[H1, H-1]/ω=0,保持了时间反演对称性,这也意味着高频光场在考虑高阶围绕对于零阶哈密顿量的修正的情况下无法引入拓扑非平庸的相。
Semi-Dirac fermion相兼具Dirac fermion和quadratic band touch相的特点,沿一个方向呈线性色散,沿着另一方向则具有抛物线色散关系,这类色散关系也在VO2-TiO2异质结和有机半导体α-(BEDT-TTF)2I3中被观察到[34-35]。
SO(3) fermion也被称为quasi-spin-1 fermion。广义的狄拉克-外尔方程可以用来描述它的行为:HΨ=(S·K)Ψ=EΨ,其中S为SO(3)群对应的Pauli矩阵,K=(kx, ky)为电子的动量。最明显的特征便是它的狄拉克点是三重简并的,其能带结构由一条平带和两条线性色散的能带组成,它同样具有Dirac fermion具有的Klein隧穿等特性[36]。目前在Lieb lattice的光晶格上已经观察到SO(3) fermion[37-39]。
由于SS格子中存在能带简并(X-K-Y以及Γ-K),所以一般的数值计算程序在计算拓扑不变量时会出现发散。为了研究这4种相的拓扑性质,我们利用体态-边缘态对应原则,考虑自旋轨道耦合打开能隙之后的情况。
3 自旋轨道耦合效应以及对边缘态的影响由于SS格子在X方向和Y方向上没有镜面对称性,所以当电子沿这2个方向做最近邻跃迁时受到不对称的作用力,产生自旋轨道耦合作用。自旋轨道耦合仅对最近邻跃迁项造成修正,所以不会造成能带的劈裂,仅仅会引入能隙使得原先的半金属变成绝缘体。引入自旋轨道耦合tsoc之后的能带和态密度如图 2所示。

|
Download:
|
| 图 2 自旋轨道耦合强度tsoc=0.2时4种相的能带结构和态密度图 Fig. 2 Band structures and densities of states of the four phases with the spin-orbit coupling parameter tsoc=0.2 | |
从图 2可以看出,4种无能隙的激发都打开了能隙,但是Dirac fermion和semi-Dirac fermion相打开的能隙非常小,quadratic band touch和SO(3) fermion相打开的能隙较大。能隙使原先没有自旋轨道耦合时的相边界消失,整个体系全部成为绝缘体。如果把矢量势A认为是绝热变化的参数,那么上面的结论意味着随着参数的演变,能隙不会发生闭合,上述所有相都是拓扑等价的。为验证这个结论,我们利用体态-边缘态对应原则计算了SS裁剪形成纳米带的能带结构,如图 3所示。

|
Download:
|
| 图 3 4种无能隙激发相在无自旋轨道耦合(a)及自旋轨道耦合强度tsoc=0.2(b)时的纳米带能带 Fig. 3 Band structures for the four gapless phases of the nanoribbon without the spin-orbit coupling(a) and band structures with the spin-orbit coupling parameter tsoc=0.2(b) | |
没有打开自旋轨道耦合作用时,边缘态连通能带的接触点,与Dirac fermion相对比,可以看出quadratic band touch, semi-Dirac fermion和SO(3) fermion都是2个Dirac point无限靠近时的特殊情形。考虑自旋-轨道耦合作用后,4种无能隙激发态都打开能隙。与体态相对应的,Dirac fermion和semi-Dirac fermion打开的能隙非常小,而quadratic band touch和SO(3) fermion打开的能隙较大。原有的边缘态劈裂成为两条并且连通价带和导带,它们相交于布里渊区边界的时间反演不变点,说明这4种激发都对应着拓扑绝缘体,其拓扑不变量为Z2不变量。
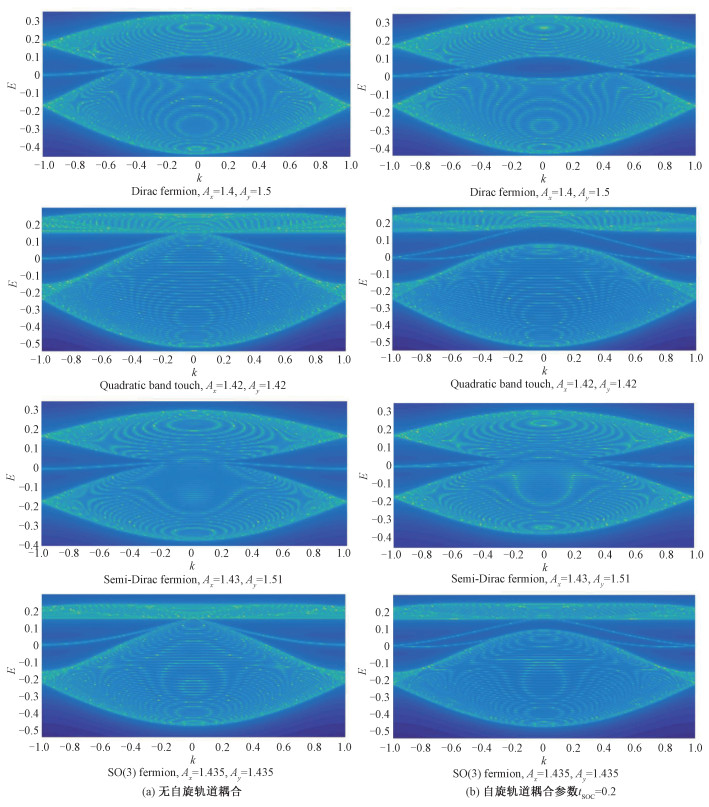
为方便实验检验,我们利用格林函数方法计算了这几种激发的局域态密度,如图 4所示。
|
Download:
|
| 图 4 纳米带在无自旋轨道耦合(a)和自旋轨道耦合参数tsoc=0.2(b)时的局域态密度 Fig. 4 Local density of states for the nanoribbon without the spin-orbit coupling (a) and with the spin-orbit coupling (the coupling parameter tsoc=0.2)(b) | |
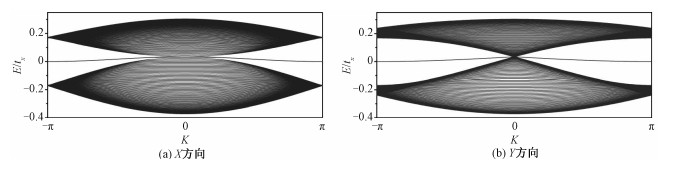
可以看出,局域态密度和图 3中的能带基本吻合。我们还发现semi-Dirac fermion的各向异性也存在于纳米带之中,这也是另一种SS格子中的体态-边缘态对应。分别计算沿X方向裁剪的纳米带和沿Y方向裁剪的纳米带的能带图,如图 5所示。
|
Download:
|
| 图 5 Semi-Dirac fermion沿X方向(a)和Y方向(b)裁剪的纳米带能带图 Fig. 5 Band structures of the semi-Dirac fermion nanoribbon truncated along the X-(a) and Y-(b) directions | |
从图 5可以看出,由于semi-Dirac fermion沿X方向和沿Y方向分别对应着抛物线型色散关系和线性色散关系,当把块体材料裁剪成为纳米带之后,能带的投影依然保持了色散关系的各向异性,沿X方向裁剪的纳米带是抛物线型色散关系,与quadratic band touch类似。而沿Y方向裁剪的纳米带,与之对应的是线性色散,与Dirac fermion类似。
为验证结论的一般性,用semi-Dirac的低能有效哈密顿量[36]
| $ \mathit{\boldsymbol{H}} = \left( {\begin{array}{*{20}{c}} 0&{\frac{{k_x^2}}{{2m}} + {\rm{i}}c{k_y}}\\ {\frac{{k_x^2}}{{2m}} - {\rm{i}}c{k_y}}&0 \end{array}} \right), $ | (9) |
令X方向为抛物线色散,有效质量为m,Y方向为线性色散,费米速度为c。利用替换(10)将低能有效哈密顿量退化为正方格子上的紧束缚模型[40]
| $ {k_i} \to \frac{1}{a}\sin \left( {a{k_i}} \right),k_i^2 \to \frac{1}{{{a^2}}}\left[ {1 - \cos \left( {a{k_i}} \right)} \right]. $ | (10) |
为了计算边缘态,把二维哈密顿量拆解成为一维链内和链间耦合两部分,并且使用表面格林函数递归方法计算局域态密度。以沿着X方向裁剪的纳米带为例,链内和链间耦合哈密顿量分别为
| $ {\mathit{\boldsymbol{H}}_0} = \left( {\begin{array}{*{20}{c}} 0&{\frac{{k_x^2}}{{2m}}}\\ {\frac{{k_x^2}}{{2m}}}&0 \end{array}} \right),{\mathit{\boldsymbol{H}}_1} = \left( {\begin{array}{*{20}{c}} 0&{{\rm{i}}c{k_y}}\\ 0&0 \end{array}} \right). $ | (11) |
计算表面格林函数的迭代算法[41]为
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}_0} = {\left( {\mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{H}}_0} - {\mathit{\boldsymbol{H}}_1}\mathit{\boldsymbol{T}}} \right)^{ - 1}},\\ \mathit{\boldsymbol{T}} = {\left( {\mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{H}}_0} - {\mathit{\boldsymbol{H}}_1}\mathit{\boldsymbol{T}}} \right)^{ - 1}}{\mathit{\boldsymbol{T}}^\dagger }. \end{array} $ |
G0是表面格林函数,T为链间转移矩阵。局域态密度ρ=-ImTrG0/π.
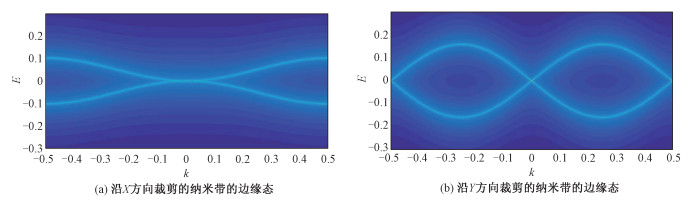
利用快速收敛算法[41], 可以计算得到沿着X方向和沿着Y方向裁剪的纳米带边界上的局域态密度,如图 6所示。
|
Download:
|
| 图 6 Semi-Dirac fermion低能等效哈密顿量对应的边缘态 Fig. 6 Edge states corresponding to the low-energy effective Hamiltonian of semi-Dirac fermion | |
由于所用哈密顿量为低能有效哈密顿量,所以得到的局域态密度只是对应于semi-Dirac fermion的边缘态。与图 5对比,可以看出这正是体态的包络。而图 5中由于拓扑性质产生的连接2个狄拉克点的边缘态在图 6中没有对应。从图 6中可以非常明显地看出在Γ点附近,垂直于X方向投影的边缘态呈抛物线形状的色散(图 6(a)),而垂直于Y方向投影的边缘态呈线性色散关系(图 6(b))。证明SS格子在semi-Dirac fermion相呈现出的各向异性就是来自于semi-Dirac fermion的各向异性色散关系。
综上所述,由于自旋轨道耦合作用引起的能隙无法闭合,所以Dirac fermion, quadratic band touch, semi-Dirac fermion和SO(3) fermion在打开能隙之后是拓扑等价的。当能隙关闭,可以认为后三者是Dirac点被光场移动到重合之后出现的特殊能带色散,它们并不被任何对称性所保护,所以一旦打开能隙,就迅速退化回到拓扑绝缘体相。
4 总结通过Floquet理论在高频近似下获得Shastry-Sutherland格子在圆偏振光场下的Floquet紧束缚哈密顿量。发现在自旋轨道耦合作用下,4种无能隙激发(Dirac fermion, quadratic band touch, semi-Dirac fermion和SO(3) fermion)都打开了能隙,而且在光场作用下能隙无法关闭,从而说明这几种无能隙激发是拓扑等价的。进而计算其边缘态,发现2条手性边缘态相交于布里渊区边界的时间反演不变点,利用体态-边缘态对应,证明这4种等价的拓扑相即是拓扑绝缘体。进一步给出局域态密度以方便实验检验。
除此之外,还发现semi-Dirac fermion的各向异性色散关系在纳米带上同样存在体态-边缘态对应,并利用semi-Dirac fermion的低能有效哈密顿量和表面格林函数算法证明了结论的一般性。
| [1] |
Novoselov K S, Geim A K, Morozov S V, et al. Electric field effect in atomically thin carbon films[J]. Science, 2004, 306(5696): 666. Doi:10.1126/science.1102896 |
| [2] |
Neto A H C. The electronic properties of graphene[J]. Review of Modern Physics, 2009, 81: 109. Doi:10.1103/RevModPhys.81.109 |
| [3] |
Kane C L, Mele E J. Quantum spin hall effect in graphene[J]. Physical Review Letters, 2005, 95(22): 226801. Doi:10.1103/PhysRevLett.95.226801 |
| [4] |
Hsieh D, Qian D, Wray L, et al. A topological Dirac insulator in a quantum spin Hall phase[J]. Nature, 2009, 452(7190): 970. |
| [5] |
Hsieh D, Xia Y, Wray L, et al. Observation of unconventional quantum spin textures in topological insulators[J]. Science, 2009, 323(5916): 919-922. Doi:10.1126/science.1167733 |
| [6] |
Thouless D J, Kohmoto M, Nightingale M P, et al. Quantized hall conductance in a two-dimensional periodic potential[J]. Physical Review Letters, 1982, 49(6): 405-408. Doi:10.1103/PhysRevLett.49.405 |
| [7] |
Kane C L, Mele E J. Z-2 topological order and the quantum spin hall effect[J]. Physical Review Letters, 2005, 95(14): 146802. Doi:10.1103/PhysRevLett.95.146802 |
| [8] |
Fu L, Kane C L, Mele E J, et al. Topological insulators in three dimensions[J]. Physical Review Letters, 2007, 98(10): 106803. Doi:10.1103/PhysRevLett.98.106803 |
| [9] |
Fukui T, Hatsugai Y, Suzuki H, et al. Chern numbers in discretized brillouin zone: efficient method of computing (spin) hall conductances[J]. Journal of the Physical Society of Japan, 2005, 74(6): 1674-1677. Doi:10.1143/JPSJ.74.1674 |
| [10] |
Fukui T, Hatsugai Y. Quantum spin hall effect in three dimensional materials: lattice computation of Z2 topological invariants and its application to Bi and Sb[J]. Journal of the Physical Society of Japan, 2007, 75: 53702. |
| [11] |
Yu R, Qi X L, Bernevig A, et al. An equivalent expression of Z2 topological Invariant for band insulators using non-Abelian Berry's connection[J]. Physical Review B, 2011, 84(7): 2250-2262. |
| [12] |
Shastry B S, Kumar B. SrCu2(BO3)2: a unique Mott Hubbard insulator[J]. Progress of Theoretical Physics Supplement, 2002, 145: 1-16. Doi:10.1143/PTPS.145.1 |
| [13] |
Romhanyi J, Karlo P, Ganesh R. Hall effect of triplons in a dimerized quantum magnet[J]. Nature Communication, 2015, 6: 6805. Doi:10.1038/ncomms7805 |
| [14] |
Kariyado T, Hatsugai Y. Symmetry-protected quantization and bulk-edge correspondence of massless Dirac fermions application to the fermionic Shastry-Sutherland model[J]. Physical Review B, 2013, 88: 245126. Doi:10.1103/PhysRevB.88.245126 |
| [15] |
Kariyado T, Hatsugai Y. Emergence of topologically stable Dirac dispersions in a Fermionic Shastry-Sutherland Model[J]. JPS Conference Proceedings, 2014, 1: 012001. |
| [16] |
Gómezleón Á, Delplace P, Platero G. Engineering anomalous quantum Hall plateaus and antichiral states with ac fields[J]. Physical Review B, 2014, 89(20): 747-751. |
| [17] |
Delplace P, Gomezleon A, Platero G, et al. Merging of Dirac points and Floquet topological transitions in AC driven graphene[J]. Physical Review B, 2013, 88(24): 5952. |
| [18] |
Inoue J, Tanaka A. Photoinduced transition between conventional and topological insulators in two-dimensional electronic systems[J]. Physical Review Letters, 2010, 105(1): 017401. Doi:10.1103/PhysRevLett.105.017401 |
| [19] |
Calvo H L, Pastawski H M, Roche S, et al. Tuning laser-induced band gaps in graphene[J]. Applied Physics Letters, 2011, 98(23): 1. |
| [20] |
Zhai X, Jin G. Photoinduced topological phase transition in epitaxial graphene[J]. Physical Review B, 2014, 89(23): 130-135. |
| [21] |
Oka T, Aoki H. Photovoltaic Hall effect in graphene[J]. Physical Review B, 2009, 79(16): 081406. |
| [22] |
Kibis O V. Metal-insulator transition in graphene induced by circularly polarized photons[J]. Physical Review B, 2010, 81: 165433. Doi:10.1103/PhysRevB.81.165433 |
| [23] |
Lindner N, Refael G, Galitski V. Floquet topological insulator in semiconductor quantum wells[J]. Nature Physics, 2010, 7(6): 490-495. |
| [24] |
Usaj G, Perez-Piskunow P M, Foa Torres L E F, et al. Irradiated graphene as a tunable Floquet topological insulator[J]. Physical Review B, 2014, 90: 115423. Doi:10.1103/PhysRevB.90.115423 |
| [25] |
Xiong T S, Gong J, An J H. Towards large-Chern-number topological phases by periodic quenching[J]. Physical Review B, 2016, 93(18): 184306. Doi:10.1103/PhysRevB.93.184306 |
| [26] |
Kitagawa T, Oka T, Brataas A, Fu L, et al. Transport properties of nonequilibrium systems under the application of light: Photoinduced quantum Hall insulators without Landau levels[J]. Physical Review B, 2011, 84: 235108. Doi:10.1103/PhysRevB.84.235108 |
| [27] |
Rudner M S, Lindner N H, Berg E, et al. Anomalous edge states and the bulk-edge correspondence for periodically-driven two dimensional systems[J]. Physical Review X, 2013, 3(3): 360. |
| [28] |
Perez-Piskunow P M, Usaj G, Balseiro C A, et al. Floquet chiral edge states in graphene[J]. Phys Rev B, 2014, 89: 12140. Doi:10.1103/PhysRevE.89.012140 |
| [29] |
Grifoni M, Hanggi P. Driven quantum tunneling[J]. Physics Reports, 1998, 304(5/6): 229-354. |
| [30] |
Kohler S, Lehmann J, Hanggi P. Driven quantum transport on the nanoscale[J]. Phys Rep, 2003, 406: 379-443. |
| [31] |
Sambe H. Steady states and quasienergies of a quantum-mechanical system in an oscillating field[J]. Phys Rev A, 1973, 7: 2203. Doi:10.1103/PhysRevA.7.2203 |
| [32] |
Sun K, Yao H, Fradkin E, et al. Topological insulators and nematic phases from spontaneous symmetry breaking in 2D fermi systems with a quadratic band crossing[J]. Physical Review Letters, 2009, 103(4): 046811. Doi:10.1103/PhysRevLett.103.046811 |
| [33] |
Kai S, Fradkin E. Time-reversal symmetry breaking and spontaneous anomalous Hall effect in Fermi fluids[J]. 2008, 78(24): 1879-1882.
|
| [34] |
Sun K, Gu Z, Katsura H, et al. Nearly flatbands with nontrivial topology[J]. Physical Review Letters, 2011, 106+(23): 236803. Doi:10.1103/PhysRevLett.106.236803 |
| [35] |
Banerjee S, Singh R R P, Pardo V, et al. Tight-binding modeling and low-energy behavior of the semi-Dirac point[J]. Physical Review Letters, 2009, 103: 016402. Doi:10.1103/PhysRevLett.103.016402 |
| [36] |
Montambaux G, Piechon F, Fuchs J N, et al. Merging of Dirac points in a two-dimensional crystal[J]. Physical Review B, 2009, 80: 153412. Doi:10.1103/PhysRevB.80.153412 |
| [37] |
Fang A, Zhang Z Q, Louie S G, et al. Klein tunneling and supercollimation of pseudospin-1 photons[J]. Physical Review B, 2016, 93: 035422. Doi:10.1103/PhysRevB.93.035422 |
| [38] |
Mukherjee S, Spracklen A, Choudhury D, et al. Observation of a localized flat-band state in a photonic Lieb lattice[J]. Physical Review Letters, 2015, 114(24): 245504. Doi:10.1103/PhysRevLett.114.245504 |
| [39] |
Vicencio R A, Cantillano C, Morales-Inostroza L, et al. Observation of localized states in Lieb photonic lattices[J]. Physical Review Letters, 2015, 114(24): 245503. Doi:10.1103/PhysRevLett.114.245503 |
| [40] |
Chu R L, Shan W Y, Lu J, et al. Surface and edge states in topological semimetals[J]. Physical Review B, 2011, 83: 075110. Doi:10.1103/PhysRevB.83.075110 |
| [41] |
Sancho M P L, Sancho J M L, Rubio J. Highly convergent schemes for the calculation of bulk and surface Green functions[J]. J Phys F: Met Phys, 1983, 14: 1205. |
 2019, Vol. 36
2019, Vol. 36 


