2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
气温作为重要的气象参数之一,被广泛运用于自然灾害监测、农业生产、生态环境评价、全球气候变化等研究领域[1-5]。气温数据的直接获取依赖于气象站点的观测数据,然而受地形、成本等因素的限制,实际上气象站点的数量有限且分布稀疏,所获得气温只能是以点代面。为了研究区域性或某些地点的气温变化规律,往往需要借助于气象站点的实际观测数据,利用空间插值的方法对未知区域、未知点的气温值进行估算,因此,气温的空间插值对于科学研究及农业生产等具有重要意义。
气温空间插值的方法主要有反距离权重法(inverse distance weighting, IDW)、普通克里金法(ordinary Kriging, OK)、样条函数法(thin plate splines, TPS)、梯度距离平方反比法(gradient plus inverse distance squared,GIDS)等。反距离权重法算法简单,是最常用的空间插值方法之一,但当样本点分布不均时插值结果会产生较大的偏差,且容易受到极值点的影响[6-7];普通克里金法考虑空间随机场的结构特点,进行最佳线性无偏估计,有效提高插值精度,广泛应用于地学的各个领域,但该方法计算复杂,变程的确定以及变差函数模型的选择均需人工干预耗时耗力,具有较强的主观性[8-11];样条函数法优点是算法简单,计算量小,可以使梯度曲线更加接近样本点,具有较好的保凸性和平滑性,但是难以估计误差,且样本点稀少时插值结果偏差较大[12];梯度距离平方反比法在反距离加权插值法的基础上,考虑了气象要素随经纬度和海拔高度的梯度变化,算法简单,物理意义明确,但在地形起伏剧烈的区域插值结果会出现大的偏差[13-15]。
在以上方法基础上,考虑到算法复杂度与插值结果的准确度,本文重点研究梯度距离平方反比法的气温插值特点,针对其在地形起伏区域出现的偏差问题,提出一种基于经验气温垂直递减率的改进梯度距离平方反比法(empirical adiabatic rate based gradient plus inverse distance squared, GIDS-EAR)。该方法在分别独立考虑海拔和经纬度对气温影响特性的基础上,计算气温与经纬度和海拔的偏回归系数,求解已知数据对待插值点的贡献权重,进而确定待插值点的温度值。
1 研究方法 1.1 梯度距离平方反比法梯度距离平方反比法由Nalder和Wein于1998年提出[14],是一种考虑了气象要素随经纬度和海拔高度变化的反距离权重法,其空间插值计算公式如下
| $ z = \frac{{(\sum\limits_{i = 1}^n {\frac{{{z_i} + \left( {x - {x_i}} \right) \times {C_x} + \left( {y - {y_i}} \right) \times {C_y} + \left( {e - {e_i}} \right) \times {C_c}}}{{d_i^2}}} )}}{{\sum\limits_{i = 1}^n {\frac{1}{{d_i^2}}} }}, $ | (1) |
式中:z表示待插点的估算值;zi为第i个样本点的实测值;di为第i个样本点与待插点之间的距离;n为参与计算的实测样本点个数;x、y、e分别为待插点的经度、纬度和海拔高度;xi、yi、ei分别为第i个样本点的经度、纬度和海拔高度;Cx、Cy、Ce分别为站点气象要素值与经度、纬度和海拔高度的偏回归系数,其值直接决定各样本点的插值权重,通过建立样本点的气象要素值与其经纬度和海拔高度的多元线性回归模型,利用最小二乘估计法对这3个系数进行求解,回归模型如下
| $ \hat{z}_{i}=C_{0}+C_{x} x_{i}+C_{y} y_{i}+C_{e} e_{i}, $ | (2) |
式中:
由1.1节方法可知,样本点气象要素值与经纬度和海拔高度的关系直接决定空间插值的效果。对气温进行空间插值时,当样本点海拔与待插值点之间的海拔相差较小时,可以得到准确度较高的插值结果;但当研究区位于地形起伏剧烈区域时,待插值点与样本点的海拔高度差异较大,此时得到的偏回归系数Cx、Cy、Ce不能准确描述待插值点气温与经纬和海拔高度的关系,所得插值误差就会较大,无法满足应用需求。
本文提出基于经验气温垂直递减率的改进梯度距离平方反比法GIDS-EAR,考虑到海拔高度对气温的影响规律与经纬度不同,将海拔与经纬度的影响分开考虑,首先根据气温垂直递减率经验值确定气温与海拔高度的偏回归系数Ce,并对样本点气温值zi进行修正得到zmi,消除由于海拔的差异对气温值的影响,再将zmi代入多元线性回归模型,作为模型最小二乘求解的样本点气温的初值,解算得到气温与经纬度的偏回归系数Cx、Cy,再依据GIDS插值公式计算待插值点的温度值。本文中GIDS-EAR方法详细步骤如下:
1) Ce的确定:考虑到海拔高度对气温的影响相较于经纬度更具有规律性,气温与海拔高度的偏回归系数与样本站点区域的气温垂直递减率接近,不同于GIDS法的线性回归求解,本文以气温垂直递减率的经验值Tg作为各样本点气温值与海拔的偏回归系数Ce,即Ce=Tg;
2) Cx、Cy的求解:由于第一步中已经考虑海拔高度对待插点气温的影响,故建立只考虑经纬度的多元线性回归模型,相应地,各样本点的气温值也应进行修正以消除海拔的影响,如下
| $ \hat{z}_{m i}=C_{0}+C_{x} x_{i}+C_{y} y_{i}, $ | (3) |
式中:
| $ z_{m i}=z_{i}+\left(e-e_{i}\right) T_{g}; $ | (4) |
3) 将上述所得Cx、Cy、Ce代入式(1)中,求得基于经验气温垂直递减率的GIDS插值结果。
1.3 验证方法本文采用“交叉验证”法[16-17],从所有气象站点中,均匀选择出24个具有代表性的站点作为检验点,以平均绝对误差(mean absolute error,MAE)与均方根误差(root mean squared error,RMSE)作为评价指标,将本文提出的GIDS-EAR法与OK、IDW、GIDS法的气温插值准确度进行对比分析。MAE与RMSE的计算公式如下:
| $ {\rm{MAE}} = \sum\limits_{i = 1}^n {{\rm{abs}}} \left( {{z_{ti}} - {z_{ei}}} \right)/n, $ | (5) |
| $ {\rm{RMSE}} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{z_{ti}} - {z_{ei}}} \right)}^2}} /n} . $ | (6) |
式中:zti为第i个站点的实测值;zei为第i个站点的插值估算值;n为检验站点的总数目。
2 实验与结果分析 2.1 实验区与数据本文研究的方法主要用于提高气温插值在地形起伏剧烈的高原、山地区域的准确度,考虑到地面气象观测站分布及地形起伏情况,优选四川省作为实验区域。四川省处于青藏高原和长江中下游平原的过渡带,高低悬殊,地貌复杂。西部高原、山地的海拔多在3 000 m以上;东部盆地、丘陵的海拔多在500~2 000 m之间。
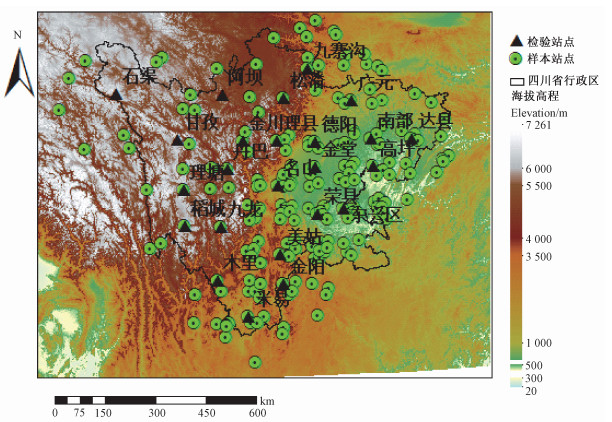
实验数据包括:四川省内及其周边地区219个地面气象站点的三维坐标、气温值及DEM数据。气温数据下载于中国气象数据网(http://data.cma.cn/site/index.html),为中国地面累年值月值气温数据集(1981—2010年);DEM数据下载于地理空间数据云(http://www.gscloud.cn/),为四川省及其周边地区的SRTMDEMUTM 90 M分辨率数字高程数据产品。气象站点分布如图 1所示,其中以海拔高程赋色,三角形代表不同地形下的检验气象站点,圆形代表样本气象站点。
|
Download:
|
| 图 1 四川省及其周边地区气象站点分布图 Fig. 1 Distribution of meteorological stations in Sichuan Province and its surroundings | |
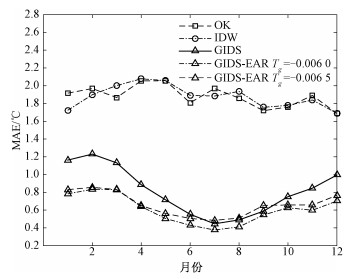
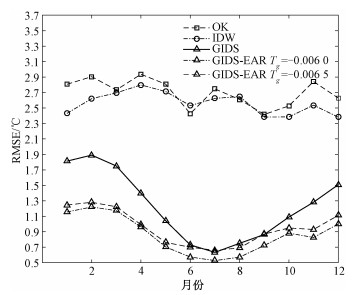
本文分别采用OK、IDW、GIDS法与GIDS-EAR法对24个检验站点12个月的气温进行插值,其中GIDS-EAR法气温垂直递减率经验值Tg取-0.006 0和-0.006 5 ℃/m[18-19]两个值进行对比分析。如表 1所示为上述4种方法得到的每个月的平均绝对误差MAE、均方根误差RMSE,图 2、图 3分别为4种方法对应的月均MAE、RMSE折线图。
|
|
表 1 4种插值方法实验验证结果 Table 1 Experimental results using the four interpolation methods |
|
Download:
|
| 图 2 检验站12个月的MAE折线图 Fig. 2 The MAE line chart for the inspection stations in a period of 12 months | |
|
Download:
|
| 图 3 检验站12个月的RMSE折线图 Fig. 3 The RMSE line chart for the inspection stations in a period of 12 months | |
由表 1及图 2、图 3可知,GIDS法与GIDS-EAR法得到的每个月的MAE和RMSE值均比OK法、IDW法的小。GIDS法得到的年均MAE及RMSE,分别比OK法的值降低56.56%、54.45%,比IDW法的年均MAE、RMSE,降低56.52%、52.02%;以Tg取-0.006 0为例,GIDS-EAR法得到的年均MAE和RMSE分别比OK法的降低67.71%、68.15%,比IDW法降低67.68%、66.45%。因此GIDS系列的插值方法所得到的气温插值效果均明显好于OK法、IDW法。
比较GIDS-EAR法与GIDS法,当Tg取-0.006 0时,GIDS-EAR法得到的每个月的MAE和RMSE均小于GIDS法,其中MAE最大减小32.63%,最小减少7.30%,RMSE最大减小36.26%,最小减少16.45%,两个指标月均分别减小23.77%和27.95%,年均分别减少25.65%和30.08%;Tg取-0.006 5时,GIDS-EAR法得到的MAE值与GIDS法相比,只在7、8、9月略大,平均增大7.92%;RMSE只在7、9月略大,平均增大0.02%;从平均水平上看,两个指标月均分别减少14.67%和18.62%,年均分别减少18.69%和22.63%。由于不同月份的实际气温垂直递减率存在细微差异[18],而文中初步尝试基于经验气温垂直递减率对GIDS方法进行改进,对不同月份使用一个固定经验值代替实际气温垂直递减率,导致不同月份GIDS-EAR法的改善效果也略有不同,甚至在7、8、9月出现误差略有增大的情况。
综上所述,进行温度插值时,GIDS-EAR法中Tg取-0.006 5和-0.006 0,其MAE值和RMSE值的平均值均小于OK、IDW、GIDS法,可知GIDS-EAR法的气温插值效果整体上优于另外3种方法;此外,气温垂直递减率Tg的取值对插值结果亦有一定影响,Tg取-0.006 0的插值精度改善效果更佳。
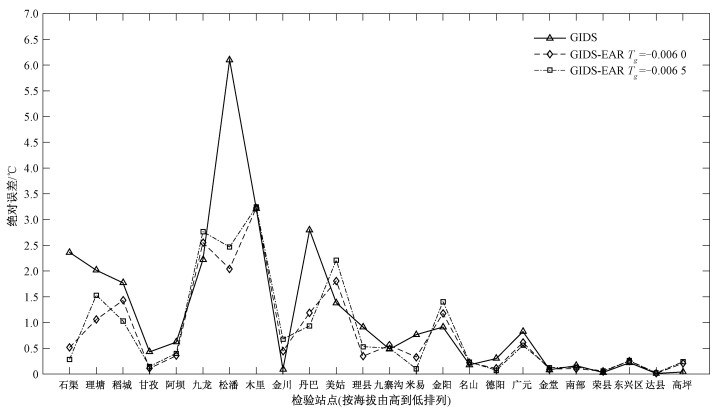
2.3 不同地形下GIDS法与GIDS-EAR法插值结果对比分析本文研究不同地形下的24个检验站点12个月的绝对误差曲线,发现检验站点12个月的绝对误差变化趋势相似,以1月份各检验站点的气温插值绝对误差曲线为例进行分析。如图 4所示为1月份各检验站点插值温度绝对误差折线,图中横坐标站点按海拔高度由高到低排列,其中石渠站位于青藏高原东南侧,理塘至金阳站除木里、美姑、金阳、米易站位于云贵高原上外,其余位于横断山脉,名山至高坪站位于四川盆地。以下从不同地形特点出发对GIDS法与GIDS-EAR法气温插值结果进行分析。
|
Download:
|
| 图 4 1月份各检验站点插值温度绝对误差折线图 Fig. 4 The absolute error line chart of interpolated temperatures at the inspection stations in January | |
从图 4可知,GIDS法插值误差最大的松潘站,采用本文提出的GIDS-EAR法后,使其误差从6.099 3 ℃降低至2.5 ℃以内,温度绝对误差改善59.54%。分析松潘站及周围样本点的海拔高度,可知松潘站海拔为2 852.1 m,样本站点的平均海拔与之相差870.545 5 m;此外,石渠、理塘、稻城、丹巴、理县、米易,这几个检验站点的海拔与其周围样本点平均海拔的高差在300~1 112 m之间,在这几个站点GIDS-EAR法得到的气温插值误差均比GIDS法的误差明显减小。说明本文提出的方法相比于GIDS法,对地形起伏剧烈的区域具有更好的适用性。
甘孜、阿坝、金川3个检验站点的海拔高度在2 000 m以上,其海拔与其周围样本站点平均海拔的高差分别为82.643、16.813、274.593 m,GIDS法得到的绝对误差均小于0.62 ℃,GIDS-EAR法得到的绝对误差均小于0.5 ℃,后者在这3个检验站点处的气温插值误差略有改善;名山至高坪这9个检验站处于四川盆地内,海拔高度均在1 000 m以下,这9个检验站的3条绝对误差曲线基本重合,GIDS法得到的MAE值为0.45 ℃;气温垂直递减率Tg分别取经验值-0.006 0、-0.006 5时,GIDS-EAR法得到的MAE分别减小9.85%、8.37%。说明检验站点与周围样本站点的海拔高差较小时,两种方法均能得到十分准确的气温值。
由于本文各站点气温垂直递减率取同一经验值,不能很好地修正部分检验站点对应的样本站点的气温值,对插值结果有一定影响,仍有待改进。如九龙、木里、金川、美姑、金阳这5个检验站点,在进行插值时,相较于GIDS法,Tg取-0.006 0、-0.006 5时,GIDS-EAR法得到的气温插值误差分别有0.01~0.43 ℃、0.01~0.8 ℃的增加,5个站点的插值气温分别平均略增0.278 9 ℃、0.498 6 ℃。
经统计分析,石渠至金阳这15个地形起伏相对剧烈的检验站的气温垂直递减率Tg分别取经验值-0.006 0、-0.006 5时,GIDS-EAR法得到的气温插值的MAE分别比GIDS法减小34.25%和30.01%。因此,本文提出的GIDS-EAR法能够比较好地克服在地形起伏剧烈区域GIDS法出现的气温插值误差较大的问题,而且在地形平缓区域得到的气温插值结果也能得到略微改善。
3 结语本文在研究梯度距离平方反比法GIDS原理的基础上,将海拔高度与经纬度对气温的影响分开考虑,提出一种基于经验气温垂直递减率的梯度距离平方反比法GIDS-EAR,并与OK、IDW、GIDS法的气温插值效果进行比较。实验结果表明GIDS-EAR法的气温插值效果要好于OK、IDW、GIDS法,当气温的垂直递减率取-0.006 0时,GIDS-EAR法得到的24个检验站点气温的年均MAE、RMSE值分别较OK法减少67.71%、68.15%,较IDW法减少67.68%、66.45%,较GIDS法减少25.65%、30.08%, 比较好地抑制了地形起伏对气温插值结果的影响,提高了对复杂地形的适用性,可对高原与山地地形的气温插值提供借鉴和参考。由于本研究初步尝试基于经验气温垂直递减率对GIDS方法进行改进,目前气温垂直递减率选取了一个固定经验值,对插值精度有一定的影响,后续可根据不同的季节、不同的海拔区间设置不同的经验值,这样可以进一步提高模型的精度。
| [1] |
崔倩.增温对大兴安岭多年冻土区泥炭地氮氧化物排放的影响研究[D].北京: 中国科学院大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-80062-1017930188.htm
|
| [2] |
丁之勇, 葛拥晓, 吉力力·阿不都外力, 等. 1957-2012年新疆艾比湖流域极端气温与降水变化趋势[J]. 中国科学院大学学报, 2018, 35(2): 160-171. |
| [3] |
姚凤梅.气候变化对我国粮食产量的影响评价[D].北京: 中国科学院研究生院, 2005. http://cdmd.cnki.com.cn/Article/CDMD-80058-2006044911.htm
|
| [4] |
姚永慧, 张百平. 青藏高原气温空间分布规律及其生态意义[J]. 地理研究, 2015, 34(11): 2084-2094. |
| [5] |
张怀坤.全球变暖条件下农业可持续发展研究[D].长春: 吉林大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011095022.htm
|
| [6] |
刘爱利, 王培法, 丁园圆. 地统计学概论[M]. 北京: 科学出版社, 2012: 96-166.
|
| [7] |
赵冰雪, 王雷, 程东亚. 安徽省气象数据空间插值方法比较与分布特征[J]. 水土保持研究, 2017, 24(3): 141-145. |
| [8] |
姜春雷.克里格插值的加速和参数优化及其应用[D].北京: 中国科学院大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-80062-1016728704.htm
|
| [9] |
李静思, 潘润秋, 范馥麟. 基于Kriging模型的地面气温空间插值研究[J]. 西南师范大学学报(自然科学版), 2016, 41(5): 21-27. |
| [10] |
李军, 游松财, 黄敬峰. 中国1961-2000年月平均气温空间插值方法与空间分布[J]. 生态环境, 2006, 15(1): 109-114. DOI:10.3969/j.issn.1674-5906.2006.01.024 |
| [11] |
戚浩平, 杨波, 路云阁, 等. 1965-2009年青藏高原地区温度的空间插值分析[J]. 东南大学学报(自然科学版), 2013(s2): 265-268. |
| [12] |
彭思岭.气象要素时空插值方法研究[D].长沙: 中南大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10533-2010187286.htm
|
| [13] |
Li J, Heap A D. A review of comparative studies of spatial interpolation methods in environmental sciences:performance and impact factors[J]. Ecological Informatics, 2011, 6(3): 228-241. |
| [14] |
Nalder I A, Wein R W. Spatial interpolation of climatic Normals:test of a new method in the Canadian boreal forest[J]. Agricultural & Forest Meteorology, 1998, 92(4): 211-225. |
| [15] |
Price D T, Mckenney D W, Nalder I A, et al. A comparison of two statistical methods for spatial interpolation of Canadian monthly mean climate data[J]. Agricultural & Forest Meteorology, 2000, 101(2): 81-94. |
| [16] |
谭剑波, 李爱农, 雷光斌. 青藏高原东南缘气象要素Anusplin和Cokriging空间插值对比分析[J]. 高原气象, 2016, 35(4): 875-886. |
| [17] |
张锦明, 游雄, 万刚. DEM插值参数优选的试验研究[J]. 测绘学报, 2014, 43(2): 178-185. |
| [18] |
江净超, 刘军志, 秦承志, 等. 中国近地表气温直减率及其季节和类型差异[J]. 地理科学进展, 2016, 35(12): 1538-1548. |
| [19] |
马新萍, 白红英, 郭帅, 等. 秦岭太白山气温垂直递减率研究[J]. 干旱区资源与环境, 2017, 31(7): 139-144. |
 2019, Vol. 36
2019, Vol. 36 


