2. 西安交通大学航天航空学院 机械结构与强度国家重点实验室, 西安 710049
2. State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace Engineering, Xi'an Jiaotong University, Xi'an 710049, China
液态金属自由表面作为聚变材料早在20世纪70年代就被提出[1],在20世纪90年代末面向等离子体部件(plasma facing components, PFCs)概念提出后,引起聚变界的重视和研究兴趣,在美国的ALPS (Advanced Limiter-divertor Plasma- facing Systems)计划中占有核心地位。而液态金属射流作为液态金属自由表面的3种形式(液膜、射流、液帘)之一,被认为有可能成为未来液态偏虑器/限制器的选用形式(要求其有足够的射程、不断开、不变形等等)[2]。
关于射流及其破碎的研究已有一个多世纪。由于射流的表面能并非最小,因而其必然会破碎[3]。导致射流破碎的直接原因就是射流界面处的扰动。对于单相、无黏射流,当扰动波长为射流圆周的143.7%时,射流最为不稳定[4]。然而,入射流体黏性能够增加射流的稳定性、抑制射流破碎、增大破碎液滴的尺寸[5]。单相射流破碎的主要物理机理即为毛细收缩(capillary pinching)[6],此外,界面扰动频率对射流破碎也有重要影响[7]。对于气-液两相射流,环境气体的黏性、密度同时对射流破碎有非常大的影响。例如:在限定的界面扰动下,存在最优的气-液黏性比使射流最为不稳定[8]。同时,当气体惯性力(正比于气体的密度)远大于单位面积的表面张力时,则在气-液界面处产生远小于射流半径的液滴,即:雾化。此外,影响射流破碎的因素还有喷口湍动、喷口速度剖面、喷口内部气蚀等[9-11]。
对于限定的气-液两相射流,影响其破碎的主要作用力包括:表面张力、惯性力及黏性剪切应力。随着喷口速度的逐渐增大,3种作用力对射流破碎的影响程度也将随之改变,射流因此可以表现出不同的破碎特征。根据破碎特征的不同,除去滴落体制以外,射流可以被分为以下4个阶段:(A)瑞利破碎体制;(B)一阶迎风破碎体制;(C)二阶迎风破碎体制;(D)雾化。在每个阶段射流都有其各自的判别准则,并且其受到的主要作用力及其破碎机理各不相同。在滴落体制(WeL=ρLDU2/σ < 8)下,流动主要受表面张力作用,惯性力和气动力可略[12]。此时,射流还未形成,流动在喷口附近即破碎,破碎长度近似于0,破碎液滴直径大于出口直径。在瑞利破碎体制(WeL>8且Weg=ρgDU2/σ < 0.4 or 1.2+3.41Oh0.9[13],其中, Oh=WeL0.5/ReL,ReL=ρLDU/μL)下,射流开始形成但仍主要受表面张力作用。射流的破碎长度(Lb/D)在10~110之间,破碎液滴直径大于射流直径。在一阶迎风破碎体制(1.2+3.41Oh0.9 < Weg < 13.0)下,射流主要受表面张力及周围气体惯性力作用(约为表面张力的10%,已不可忽略)。射流破碎长度在110~60之间,破碎液滴直径等于射流直径。在二阶迎风破碎体制(13.0 < Weg < 40.3)下,射流仍主要受表面张力及气体惯性力(与表面张力同阶)作用。射流的破碎长度在60~100之间;破碎液滴直径小于射流直径。在雾化体制(Weg>40.3)下,射流所受气体惯性较大于表面张力。射流在喷口处即破碎,破碎液滴直径远小于射流直径[14]。
当导电流体射流处于磁场中时,受到洛仑兹力作用。洛仑兹力打破了已知4种破碎体制下3种作用力原有的地位,使得射流的破碎机理变得更为复杂。这也使得磁场中导电射流研究变得更为困难,处于磁场中导电射流也因此表现出更多新颖和多样化的破碎特征。例如:实验发现水平的导电流体细长射流在非均匀磁场的作用下,其截面形状会随射流的发展逐渐沿磁场方向拉伸,且磁场强度越强,其位伸越为明显[15];导电圆柱射流在同轴对称磁场中所受洛仑兹力,在瑞利破碎体制下会大大增强其稳定性,使之不易破碎[16-17]。本文主要就处于横向水平垂直磁场中的液态金属竖直射流进行三维的直接数值模拟研究。
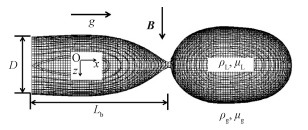
1 计算物理模型本文计算物理模型如图 1所示。射流在与之平行的重力场g和与之垂直的磁场B的作用下,从直径为D的喷口射出。射流破碎时的长度为Lb。出射流体的黏性为μL、密度ρL、电导率σL。与之对应地,环境流体的黏性为μg、密度ρg、电导率σg。
|
Download:
|
| 图 1 水平磁场中液态金属射流的物理模型示意图 Fig. 1 Physical model of the liquid metal jet under the horizontal magnetic field | |
本文模型计算的相关不可压缩流体力学方程分别为:质量守恒、动量方程、欧姆定律以及电荷守恒方程,其表达式如下:
| $ \nabla \cdot \boldsymbol{V}=0, $ | (1) |
| $ \begin{aligned} \rho\left(\partial_{t} \boldsymbol{V}+\boldsymbol{V} \cdot \nabla \boldsymbol{V}\right)=&-\nabla_{p}+(\boldsymbol{j} \times \boldsymbol{B})+\\ & \mu \Delta \boldsymbol{V}+\rho g ~\hat{\boldsymbol{e}}_{\mathrm{g}}, \end{aligned} $ | (2) |
| $ \boldsymbol{j}=\sigma(-\nabla \boldsymbol{\phi}+\boldsymbol{V} \times \boldsymbol{B}), $ | (3) |
| $ \nabla \cdot \mathit{\boldsymbol{j}} = 0. $ | (4) |
式中:V=(u, v, w)为流体速度矢量;ρ为流体密度;μ为动力黏性系数;p为压强;g为重力加速度;
| $ \nabla \cdot \boldsymbol{V}^{*}=0, $ | (5) |
| $ \begin{array}{c}{\frac{1}{N}\left(\partial_{t}^{*} \boldsymbol{V}^{*}+\boldsymbol{V}^{*} \cdot \nabla \boldsymbol{V}^{*}\right)=-\nabla_{p}^{*}+\left(\boldsymbol{j}^{*} \times \boldsymbol{B}^{*}\right)+} \\ {\frac{1}{N R e} \Delta \boldsymbol{V}^{*}+\frac{1}{N F r} \hat{\boldsymbol{e}}_{\rm{g}}}, \end{array} $ | (6) |
| $ {\mathit{\boldsymbol{j}}^*} = \sigma \left( { - \nabla {\phi ^*} + {\mathit{\boldsymbol{V}}^*} \times {\mathit{\boldsymbol{B}}^*}} \right), $ | (7) |
| $ \nabla \cdot {\mathit{\boldsymbol{j}}^*} = 0. $ | (8) |
式中:N数为相互作用数,表示磁场力与惯性力之比;Fr为费劳德数,表示惯性力与重力之比;Re为雷诺数,表示惯性力与黏性力之比。它们表达式分别如下:
| $ N=\frac{D \boldsymbol{B}^{2} \boldsymbol{\sigma}}{\rho V_{0}}, F r=\frac{V_{0}^{2}}{g D}, R e=\frac{\rho V_{0} D}{\mu}. $ |
此外,本文同时还引入无量纲形式的哈特曼数——Ha数,其定义式如下
| $ Ha = \mathit{\boldsymbol{B}}D\sqrt {\frac{\sigma }{\mu }} . $ |
在求解流体动力学方程(5)、方程(6)时,本文使用自适应的直角网格辅之以两步投影法求解速度-压力耦合场[18]。在求解磁流体动力学方程(7)、方程(8)时,本文采用相容守恒性格式[19]求解电磁场,该离散主要分两步:
1) 通过泊松方程求解电势方程:
| $ \nabla_{\mathrm{c}} \cdot\left(\nabla_{\mathrm{f}} \phi^{k+1 / 2}\right)=\nabla_{\mathrm{c}} \cdot\left((\boldsymbol{V} \times \boldsymbol{B})_{\mathrm{f}}^{k}\right), $ | (9) |
式中:f表示网格单元表面变量,c表示网格单元中心变量;
2) 在单元表面通过相容格式直接计算电流密度:
| $ \begin{aligned}\left(\boldsymbol{j}_{n}\right)_{\mathrm{f}}^{k+1 / 2}=&(\boldsymbol{j} \cdot \boldsymbol{n})_{\mathrm{f}}^{k+1 / 2}=\\ &\left(\left(-\nabla_{\mathrm{f}} \boldsymbol{\phi}^{k+1 / 2}\right)+(\boldsymbol{V} \times \boldsymbol{B})_{\mathrm{f}}^{k}\right) \cdot n_{\mathrm{f}}. \end{aligned} $ | (10) |
然后,将单元表面电流密度插值得到单元中心电流密度进而计算洛仑兹力。本文使用的模拟程序为实验室开发的MHD多相流数值算法程序,应用该程序我们计算了液滴在磁场中与液膜的撞击和铺展,经验证其在MHD数值模拟方面有着很好的精确性和稳定性[20]。时间步在确定CFL < 0.5条件下由程序自动设定。
3 结果分析射流破碎的主要特征包括主射流破碎长度、破碎液滴尺寸等,而影响射流破碎的主要因素有惯性力、表面张力、黏性力以及空气动力。当射流处于磁场中时,磁场对射流破碎的影响是巨大的,无论是破碎特征还是破碎的机理方面。本节主要从破碎长度、内部流动、涡结构截面形状几方面介绍磁场对射流破碎的作用并机理分析。
3.1 射流的破碎长度射流的破碎长度主要受界面扰动及射流稳定性的影响。已知黏性具有稳定射流的作用[18],表面毛细作用是射流破碎的根本原因[8],空气动力对射流破碎起到或大或小的加剧作用。此外,随着惯性力的增加,引起射流的破碎主要作用力不同,其又可分为4种不同的破碎体制。然而,在磁场中随磁场力的逐渐增大,射流的破碎也会表现出不同的破碎特征。
本文主要研究处于水平磁场中的滴落体制、瑞利破碎体制射流的破碎长度。首先考虑无磁场情形,这时射流破碎长度的经验公式[11, 21]主要形式有以下3种:
| $ L_{\mathrm{b}} / D=0.5 W e_{\mathrm{L}}^{-0.4} R e_{\mathrm{g}}^{0.6}, $ | (11) |
| $ L_{\mathrm{b}} / D=2.2 W e_{\mathrm{L}}^{0.28} F r^{0.78}, $ | (12) |
| $ L_{\mathrm{b}} / D=C W e^{0.5}(1+3 O h). $ | (13) |
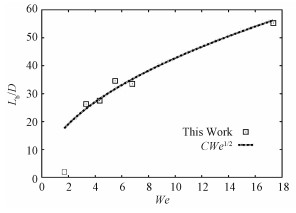
本文对无磁场情形的液态金属射流破碎也进行了模拟,如图 2所示。由图可见,除小We数(We < 2)情形,本文模拟结果与线性稳定性分析的结果式((13))符合得非常好。
|
Download:
|
| 图 2 无磁场情形液态金属射流的破碎长度随We数的变化关系 Fig. 2 Relationship between the breakup length and We without magnetic field | |
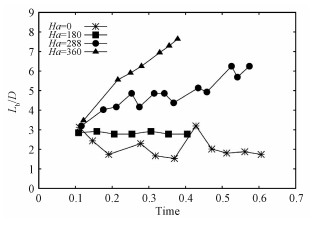
在水平磁场的作用下,射流的破碎长度有着极大的改变,如图 3所示。当We=1.695时,射流基本处于滴落体制。当Ha=0时,射流经过短暂发展,初次破碎即进入稳定的破碎流动阶段,即:射流破碎长度在一定范围内变化。当Ha=180时,射流破碎长度有稳定增长,但其仍处于滴落体制。而当Ha=288和Ha=360时,射流的破碎长度随射流发展越来越长。并且,磁场强度越强其破碎长度越长,长度增长速度也越快。
|
Download:
|
| 图 3 水平磁场中液态金属射流的破碎长度随Ha数的变化关系(We=1.695) Fig. 3 Variation in the breakup length with the Ha value under the horizontal magnetic field (We=1.695) | |
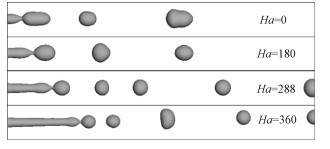
液态金属射流在磁场中最大破碎长度的对比情况如图 4所示。不难发现,不仅射流破碎形态随Ha数的增大很明显地增长,同时射流变得越来越细,射流界面扰动波的波长也越长,而射流破碎后所形成的液滴随着Ha数的增大变得越来越小。这与图 3中所示数据是相吻合的。图 3中,各Ha数情况下的初次破碎点在时间和长度上几乎是重合的(总体上,Ha数较大时,时间偏滞后,破碎长度偏大)。然而,各Ha数情况下,射流二次破碎是截然不同的。Ha数越大,破碎时间明显越滞后,对应的破碎长度也明显越长。由于Re相同,根据质量守恒,显然Ha数越大时其射流的主流段就越长。另外,二次破碎以后,射流破碎的频率随Ha数的增大变化并不明显。不同的是,在大Ha数情形下,射流的破碎长度仍然在随着破碎而增长。Ha数越大,射流的破碎长度相应增长越快。同样地,由于质量守恒,射流破碎后所形成的液滴必然随着Ha数的增大而逐渐减小。
|
Download:
|
| 图 4 水平磁场中液态金属射流在不同磁场强度下的最大破碎长度(We=1.695)对比图 Fig. 4 Comparison among the breakup cases at different Ha values under the horizontal magnetic field (We=1.695) | |
在无磁场情况下,当射流出射速度较小时,即滴落以及瑞利破碎体制下,影响射流破碎及形态的主要因素为表面张力。然而,射流在磁场中还将受洛伦兹力作用,并且洛伦兹力随着磁场增强而增强。在表面张力及洛伦兹力的共用作用下,射流的破碎长度得到延长。不难得出,在滴落体制下,射流在水平磁场中感应所产生的洛伦兹力对射流主流段的稳定性有很强的增强作用。
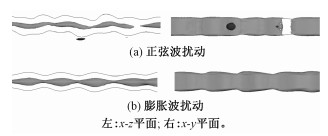
3.2 界面扰动射流的界面扰动主要有均匀段、膨胀波扰动和正弦波扰动3种形式[3]。在无磁场情形下,射流的界面扰动呈现三维特性(图 5(a))。在x-z平面以及x-y平面都可以很明显地观察到界面的扰动,这种扰动随射流的流动向下传递并呈非线性增长,最终致使射流破碎。在水平磁场中,受洛伦兹力作用,射流在x-z平面内沿磁场方向(z)的界面扰动受到抑制,其界面两边界几乎完全平行;在x-y平面内射流界面的扰动无论膨胀波还是正弦波表现的都更为明显,界面扰动由三维变为准二维情形,就像在洛伦兹力的作用下沿磁场方向(z)被拍扁了,使得扰动几乎完全集中在x-y平面内(图 5(b))。

|
Download:
|
| 图 5 水平磁场中射流界面的变形(We=61.5) Fig. 5 Deformations of the liquid metal jet under the horizontal magnetic field (We=61.5) | |
水平磁场作用下,射流的内部流动如图 6所示。可以发现,在射流内部流动的速度变化主要集中在x-y平面内的界面处,以膨胀波或正弦波的波峰为中心,形成一个个小涡。这与3.2节中的界面扰动以及射流表现形态正好相吻合。
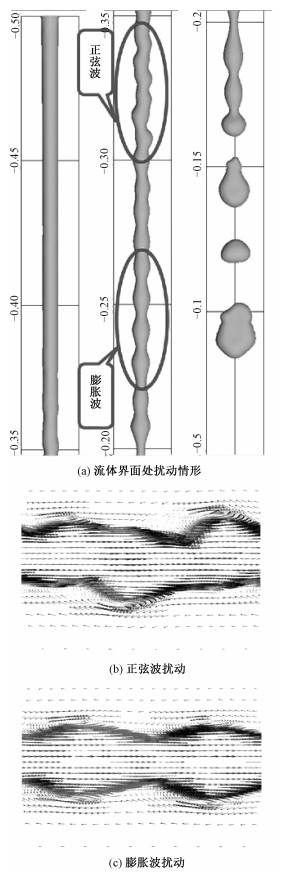
|
Download:
|
| 图 6 水平磁场中射流界面扰动情形及内部x-y平面内的速度矢量图(We=9.23, Ha=360) Fig. 6 Waves on the surface and the velocity vector in the x-y plane in different sections of the liquid metal jet(We=9.23, Ha=360) | |
然而,水平磁场对液态金属射流内部流动的影响主要表现在速度核心区,如图 7所示。受洛伦兹力作用,液态金属射流的速度核心区在x-z平面被压,而在x-y平面内得到拉伸,整个速度核心区呈现为沿y方向拉伸的扁平状。这与无磁场情形下,射流速度核心区所呈的圆柱状是截然不同的。
|
Download:
|
| 图 7 水平磁场中射流内部速度核心区等值面云图(We=9.23, Ha=360) Fig. 7 The core of the velocity in the liquid metal jet (We=9.23, Ha=360) | |
液态金属在强磁场下的流动行为的研究是目前磁约束聚变中包层及液态金属第一壁的研究热点之一,而液态金属射流被认为有可能成为未来液态偏虑器/限制器的选用形式。本文针对水平磁场中小We数情形的液态金属射流破碎,通过数值模拟的研究,阐明其在水平磁场中的运动特性。研究主要内容为其破碎的长度、内部的流动、界面扰动等几个方面,可以为实验研究提供参考。本文研究得出如下主要结论:
1) 射流的破碎长度随磁场强度的增强而逐渐增大,射流表现越稳定;
2) 射流在滴落体制下,内部流动受水平磁场影响并不明显,在较大We数情形下,射流内部流动受磁场影响明显,其内流在扰动的波峰处形成涡结构,速度核心区由圆柱状变为扁平状,垂直磁场方向被压缩;
3) 射流的界面扰动分为均匀段、膨胀波以及正弦波扰动,膨胀波和正弦波扰动在磁场的影响下,受洛伦兹力作用,表现为明显的二维特性。
| [1] |
Wells W M. A system for handling diverter ion and energy flux based on a lithium droplet cloud[J]. Nuclear Technology-Fusion, 1981, 1(1): 120-127. |
| [2] |
Kang W, Pan C, Xu Z. Application study of liquid metal free surface in fusion[J]. Science Technology and Engineering, 2006, 6(6): 731-738. |
| [3] |
Maxwell J C. Statique expérimentale et théorique des Liquides soumis aux seules Forces moléculaires[J]. Nature, 1874, 10(242): 119. DOI:10.1038/010119a0 |
| [4] |
Rayleigh L. On the capillary phenomena of jets[J]. Proceedings of the Royal Society of London, 1879, 29(196/199): 71-97. |
| [5] |
Goedde E F, Yuen M C. Experiments on liquid jet instability[J]. Journal of Fluid Mechanics, 1970, 40(3): 495-511. |
| [6] |
Alterman Z. Capillary instability of a liquid jet[J]. The Physics of Fluids, 1961, 4(8): 955-962. DOI:10.1063/1.1706445 |
| [7] |
Rutland D F, Jameson G J. A non-linear effect in the capillary instability of liquid jets[J]. Journal of Fluid Mechanics, 1971, 46(2): 267-271. |
| [8] |
Tomotika S. On the instability of a cylindrical thread of a viscous liquid surrounded by another viscous fluid[J]. Proceedings of the Royal Society A, 1935, 150(870): 322-337. DOI:10.1098/rspa.1935.0104 |
| [9] |
Leib S J, Goldstein M E. The generation of capillary instabilities on a liquid jet[J]. Journal of fluid mechanics, 1986, 168: 479-500. DOI:10.1017/S0022112086000472 |
| [10] |
Eroglu H, Chigier N, Farago Z. Coaxial atomizer liquid intact lengths[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(2): 303-308. |
| [11] |
Wu P K, Tseng L K, Faeth G M. Primary breakup in gas/liquid mixing layers for turbulent liquids[J]. Atomization and Sprays, 1992, 2(3): 295-317. DOI:10.1615/AtomizSpr.v2.i3 |
| [12] |
Lin S P, Reitz R D. Drop and spray formation from a liquid jet[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 85-105. |
| [13] |
Sterling A M, Sleicher C A. The instability of capillary jets[J]. Journal of Fluid Mechanics, 1975, 68(3): 477-495. |
| [14] |
Miesse C C. Correlation of experimental data on the disintegration of liquid jets[J]. Industrial & Engineering Chemistry, 1955, 47(9): 1690-1701. |
| [15] |
Oshima S, Yamane R, Mochimaru Y, et al. The shape of a liquid metal jet under a non-uniform magnetic field:fluids engineering[J]. JSME international journal, 1987, 30(261): 437-448. DOI:10.1299/jsme1987.30.437 |
| [16] |
Ruo A C, Chang M H, Chen F. Electrohydrodynamic instability of a charged liquid jet in the presence of an axial magnetic field[J]. Physics of Fluids, 2010, 22(4): 1917. |
| [17] |
Davidson P A. Magnetic damping of jets and vortices[J]. Journal of Fluid Mechanics, 1995, 299: 153-186. DOI:10.1017/S0022112095003466 |
| [18] |
Popinet S. Gerris:a tree-based adaptive solver for the incompressible Euler equations in complex geometries[J]. Journal of Computational Physics, 2003, 190(2): 572-600. |
| [19] |
Zhang J, Ni MJ. A consistent and conservative scheme for MHD flows with complex boundaries on an unstructured Cartesian adaptive system[J]. Journal of Computational Physics, 2014, 256(C): 520-542. |
| [20] |
Wang J J, Zhang J, Ni M J, et al. Numerical study of single droplet impact onto liquid metal film under a uniform magnetic field[J]. Physics of Fluids, 2014, 26(12): 122-129. |
| [21] |
Shibata K, Koshizuka S, Oka Y. Numerical analysis of jet breakup behavior using particle method[J]. Journal of Nuclear Science and Technology, 2004, 41(7): 715-722. DOI:10.1080/18811248.2004.9715538 |
 2019, Vol. 36
2019, Vol. 36 


