C-start is a type of burst maneuver pattern, in which the fish starts from rest and bends its body into a C shape, after which the tail flaps back and moves in a new direction[1]. It is widely believed that C-start occurs in the fish's escape response[2]. In order to avoid predatory threats or external stimuli, fish can rapidly turn and escape by using C-start[3-4]. However, experimental studies have shown that, in the absence of predatory threats and external stimuli, the zebrafish also performs a C-start to make a turn starting from rest[5]. According to the purpose of swimming, this kind of C-start is called a C-turn, whereas the C-start in escape response is called a C-escape. Zebrafish C-turns and C-escapes have different deforming modes and durations, which result in the difference in the locomotion performance: with the same bending amplitude, the speed of C-turn is not as fast as that of C-escape, but it achieves a larger turning angle. In order to explain the difference in their swimming performance, it is necessary to compare the hydrodynamics and the energetics of zebrafish's C-turn and C-escape.
Researchers previously conducted extensive studies on the hydrodynamics of C-escape. Hu et. al. numerically studied the tail-flapping model of C-start[6]. Jing et al. conducted in-vivo experimental observations and theoretical analyses of C-escapes of crucian carp and yellow catfish[7-8]. Tytell and Lauder conducted the first in-vivo PIV experiment on C-escape and found that there were three jets in the flow field[9]. Witt et al.[10] studied the effects of flexibility on C-escape with simple physical models. Liu et al.[11] performed the self-propelled simulation of C-escape for the first time, and revealed the important role of the traveling curvature wave in the C-escape. Subsequently, Gazzola et al.[12] used evolutionary optimization to prove that C-escape is the best way to achieve maximum swimming distance. Li et al.[13-14] studied the effect of the head passing through a wake vortex on the trajectory of the locomotio. Borazjani et al.[15-16] studied the role of caudal and dorsal fins. Song et al.[17] studied the rapid turning problem in larval fish's escape response. However, to the best of our knowledge, research on the hydrodynamics and energetics of zebrafish C-turn has not been reported.
Self-propelled numerical simulation is an important method to study on hydrodynamics of C-starts, which has been used for researching C-escape[11-14]. During the self-propelled simulation, the deformation action of the fish body is needed as input conditions. For steady swimming, people commonly use sine waves to describe the undulation of the fish body[18-20]. For C-escape, due to the complexity of the deformation, many previous studies used the discrete experimental data directly[13-17]. However, this requires spatio-temporal interpolation and fairness, in which the calculation is easy to divergence and repeatability is poor. Moreover it is difficult to grasp the principal characters of deformation. Liu et al. [11] and Gazzola et al. [12] established a simplified curvature model for C-escape by superimposing sinusoidal traveling waves and standing waves. However this model may not be applicable to C-turns because of the difference in the deformation pattern between C-turns and C-escapes. How does one select the model parameters so that the model is in agreement with the experiment? This problem has not been resolved either.
In this paper, we propose novel curvature models to describe the deformations of C-turn and C-escape of zebrafish. Parameters of curvature models are determined based on experimental data with an optimization algorithm. Then we perform self-propelled numerical simulation in order to explore the hydrodynamic mechanism and energetics features of C-turns and C-escapes. The influences of both the deforming mode and duration on the C-start swimming performance are discussed.
1 Materials and methods 1.1 The fish body modelThe contour of zebrafish's body is symmetrical up and down, and it can be described by the function of the half width of the fish body:
| $ \begin{array}{*{20}{c}} {{w_m}\left( s \right) = {w_1}\sqrt {\frac{s}{L}} + {w_2}\frac{s}{L} + {w_3}{{\left( {\frac{s}{L}} \right)}^2} + }\\ {{w_4}{{\left( {\frac{s}{L}} \right)}^3} + {w_5}{{\left( {\frac{s}{L}} \right)}^4},} \end{array} $ | (1) |
where s is the curve coordinate of the fish midline, L is the length of the fish body, and w1, w2, w3, w4, w5 are coefficients whose values are fitted according to the real fish body contour and listed in Table 1. The cross section of the real fish body is approximately elliptical. According to the geometric properties of the ellipse, the average half width of the fish body is w(s)=wm(s)π/4. In this paper, a two-dimensional fish model is adopted, whose half width is equal to the average half width of the real fish.
|
|
Table 1 Coefficients in the half width function |
Figure 1 gives experimental images of typical C-turn and C-escape of zebrafish, which are provided by Zhang Bingbing[5]. We can find that both the C-turn and C-escape have two stages, bending of the body and backward flapping of the tail, which is the main deformation characteristic of the C-start. The difference is that C-turns only flap back to the straight-line state at most, and the body is always bent to only one side and there is no reverse bending. However, C-escape has reversed bending after 43.7 ms. Domenici and Blake[3] classify C-start into single-bend and double-bend types based on the absence or presence of reverse bending. The C-turn is of the single-bend type, and the C-escape is of the double-bend type. In addition, the durations of C-turn and C-escape are significantly different, and the former is nearly three times the latter.

|
Download:
|
|
Fig. 1 Experimental images of zebrafish C-turn and C-escape |
|
The unilateral bending of C-turns means that the curvature of the fish midline is always positive. Therefore, we establish a curvature space model κ(s) similar to a solitary wave as shown in Fig. 2(a). It consists of five parameters. A is the amplitude of curvature, and s1, s2, s3, and s4 are the coordinates along the fish midline. This model can be described by the function
| $ \kappa \left( s \right) = f\left( {s,{s_1},{s_2},{s_3},{s_4},0,A} \right), $ | (2) |

|
Download:
|
|
Fig. 2 Curvature models and flow chart of the optimization |
|
where f is a piecewise function defined as follows:
| $ \begin{array}{*{20}{c}} {f\left( {\zeta ,{\zeta _1},{\zeta _2},{\zeta _3},{\zeta _4},{f_1},{f_2}} \right) = }\\ {{f_1} + \left( {{f_2} - {f_1}} \right)\left[ {\xi - \sin \left( {2{\rm{ \mathsf{ π} }}\xi } \right)/2{\rm{ \mathsf{ π} }}} \right],} \end{array} $ | (3a) |
| $ \xi = \left\{ {\begin{array}{*{20}{c}} {\left( {\zeta - {\zeta _1}} \right)/\left( {{\zeta _2} - {\zeta _1}} \right)}&{\zeta \in \left[ {{\zeta _1},{\zeta _2}} \right)}\\ 1&{\zeta \in \left[ {{\zeta _2},{\zeta _3}} \right]}\\ {\left( {{\zeta _4} - \zeta } \right)/\left( {{\zeta _4} - {\zeta _3}} \right)}&{\zeta \in \left( {{\zeta _3},{\zeta _4}} \right]}\\ 0&{{\rm{others}}} \end{array}} \right., $ | (3b) |
where ζ is an independent variable, and ζ1, ζ2, ζ3, ζ4, f1, and f2 are parameters. The five parameters of the curvature space model are all related to time. Their tendency to change over time is approximately illustrated in Fig. 2(b), i.e., the curvature time model, which reflects the growth and propagation of curvature. They can also be described by the function f as follows:
| $ A\left( t \right) = f\left( {t,0,{t_a},T,T,T,{A_m}} \right), $ | (4a) |
| $ {s_1}\left( t \right) = f\left( {t,{t_1},10T,10T,10T,{s_{11}},{s_{12}}} \right), $ | (4b) |
| $ s_{2}(t)=f\left(t, t_{2}, T, T, T, s_{21}, L\right), $ | (4c) |
| $ s_{3}(t)=f\left(t, 0, t_{3}, T, T, s_{31}, L\right), $ | (4d) |
| $ s_{4}(t)=f\left(t, 0, t_{4}, T, T, s_{41}, L\right), $ | (4e) |
where T is the duration of C-turns; ta, Am, t1, s11, t2, s21, t3, s31, t4, and s41 are parameters of the curvature time model. Each curve has two parameters, and their meanings are shown in Fig. 2(b) in detail. In order to makes1(t)=L, s12 should be:
| $ \begin{array}{*{20}{c}} {{s_{12}} = {s_{11}} + \left( {L - {s_{11}}} \right)/}\\ {\left[ {\frac{{T - {t_1}}}{{10T - {t_1}}} - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\sin \left( {2{\rm{ \mathsf{ π} }}\frac{{T - {t_1}}}{{10T - {t_1}}}} \right)} \right].} \end{array} $ |
For the C-escape, it is seen in Fig. 1 that the deformation in the bendding phase is very similar to the C-turn. The curvature is established gradually and propagates backward. Liu et al.[11] and Gazzola et al.[12] established a C-escape curvature model by superimposing standing waves and sinusoidal traveling waves. However, we find that this model can not reflect the deformation of the zebrafish C-escape accurately, because the standing wave does not meet the characteristics of backward propagation of curvature. Even so, the idea of superimposing sinusoidal traveling waves is worth learning. We utilise the curvature model of C-turn (i.e., Eqs. (2)-(4)), and add a sinusoidal traveling wave to model the curvature of C-escape. The sine curvature traveling wave is defined as follows:
| $ {\kappa _{\sin }}\left( {s,t} \right) = {A_{\sin }}\sigma \left( s \right)\tau \left( t \right)\sin \left[ {2{\rm{ \mathsf{ π} }}\left( {\frac{s}{\lambda } - \frac{t}{{{T_{\sin }}}}} \right) + {\phi _0}} \right], $ | (5a) |
| $ \sigma \left( s \right) = \left\{ {\begin{array}{*{20}{c}} 0&{0 \le s \le {s_{\rm{h}}}}\\ {{{\left( {\frac{s}{L}} \right)}^2} + {a_1}\frac{s}{L} + {a_0}}&{{s_{\rm{h}}} < s \le L} \end{array}} \right., $ | (5b) |
| $ \tau \left( t \right) = \left\{ {\begin{array}{*{20}{c}} 0&{0 \le t \le {t_{\rm{s}}}}\\ {\frac{{t - {t_{\rm{s}}}}}{{{t_{\rm{e}}} - {t_{\rm{s}}}}} - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\sin \left( {2{\rm{ \mathsf{ π} }}\frac{{t - {t_{\rm{s}}}}}{{{t_{\rm{e}}} - {t_{\rm{s}}}}}} \right)}&{{t_{\rm{s}}} < t \le {t_{\rm{e}}}}\\ 1&{{t_e} < {\rm{t}} \le T} \end{array}} \right., $ | (5c) |
where Asinrepresents the amplitude of the sine wave, λ is the wavelength, Tsin is the period, ϕ0 is the initial phase, a0 and a1 are coefficients of the amplitude distribution function σ(s), sh indicates the head length of the fish, and ts and te are parameters in the time function τ(t).
1.3 Determination of model parametersThere are 10 and 19 parameters in the C-turn and C-escape curvature models, respectively. The curvature models have to be consistent with the experiment. In order to identify their parameters, we used an optimization algorithm to fit the experimental data. First, we extract several discrete points on the midline of the fish body from the experimental image and convert them to the fish head coordinate system. Then we calculate the model midline with the curvature model in the fish head system. The optimal objective function is
| $ \varepsilon = \sqrt {\frac{1}{{Nt}}\frac{1}{N}\sum\limits_{it = 1}^{Nt} {\sum\limits_{i = 1}^N {\left[ {{{\left( {{x_{i,it}} - {{x'}_{i,it}}} \right)}^2} + {{\left( {{y_{i,it}} - {{y'}_{i,it}}} \right)}^2}} \right]} } } . $ | (6) |
It represents the standard deviation between the model curve and the experimental fish midline. The direction of optimization is to minimize the error. Nt is the number of experimental images (11 for C-turn and 12 for C-escape), N is the number of discrete points on the fish midline in each image (17 in this article), (xi, it, yi, it) is the coordinate in the head reference system of the ith discrete point in the itth experimental image, and (x′i, it, y′i, it) is the closest point to (xi, it, yi, it) on the model curve at the time of (it-1)/(Nt-1).
The optimization process is shown in Fig. 2(c), where pi is the ith parameter and δi expresses the iterative step length of pi, whose value is 0.01 time the unit of pi. For the C-turn, in each iteration, all the parameters are traversed in three cases, pi-δi, pi, and pi+δi. There are 310 (59 049) cases, and the parameter combination of the least error is selected. If the deviation does not converge, then the iterations continue; If the opposite is true, then the iterations terminate. For the C-escape, the parameters of the 'C-turn' model are firstly determined by the above method, and then the parameters of sine wave. The parameters should meet certain physical constraints, such as 0 < ta, t1, t2, t3, t4 < T, 0 < s11≤s21≤s31≤s41 < L for C-turn, and 0 < ts < te < T for C-escape.
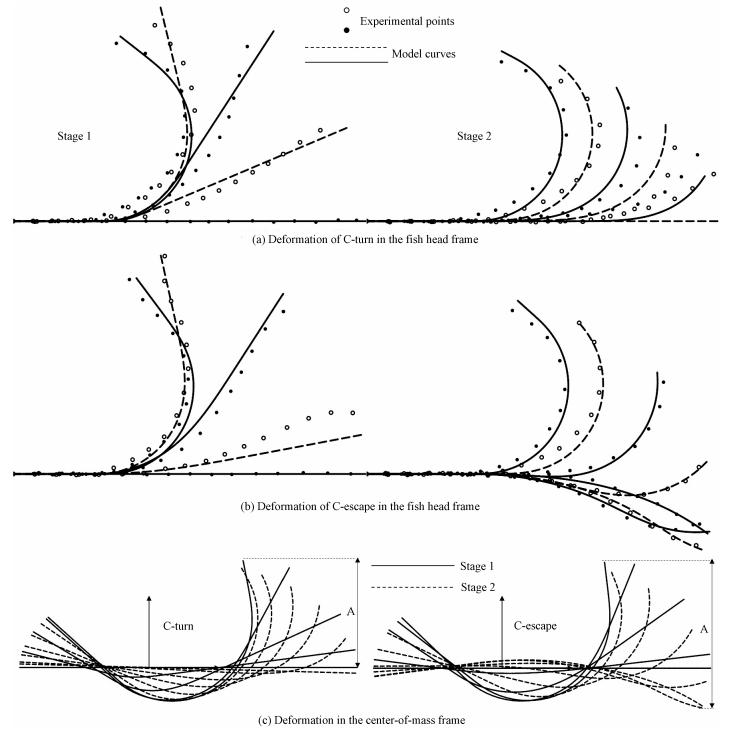
Table 2 displays the parameters of the optimized curvature model. The midline of the fish body is calculated by the curvature model and compared with the experimental points under the fish head coordinate system, as shown in Fig. 3(a), 3(b). It is observed that there is some error in the model curve compared to the experiment. At the end of the C-turn, the fish body is not completely straightened, but the model curve is fully straightened. The error for C-escape is largest at t/T=1/11, as shown in Fig. 3(b). However, as a whole, the curvature model describes the deformation of zebrafish C-turn and C-escape very well. Their errors are only 2.18% and 1.44%, respectively.
|
|
Table 2 Values of the curvature model parameters |
|
Download:
|
|
Fig. 3 Deformations of C-turn and C-escape in the fish head and center-of-mass frames |
|
Although the curvature model established in this paper has 19 parameters at most, it is much lower than the 204 discrete experimental points (12 maps, 17 points for each map). Moreover, the curvature model grasps the main features of deformation, and the curvature is smooth, which facilitates numerical simulation. The curvature model has practical guiding significance for robotic fish[21].
1.4 Governing equations of the self-propelled swimmingThe self-propelled swimming of fish is jointly controlled by the equations of fluid mechanics anddeforming body dynamics. The fluid control equations are incompressible Navier-Stokes equations
| $ \nabla \cdot \mathit{\boldsymbol{u}} = 0, $ | (7a) |
| $ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \left( {\mathit{\boldsymbol{u}} \cdot \nabla } \right)\mathit{\boldsymbol{u}} = - \frac{1}{\rho }\nabla p + \nu {\nabla ^2}\mathit{\boldsymbol{u}}, $ | (7b) |
where u, p, ρ and ν are the velocity, pressure, density, and kinematic viscosity of the fluid, respectively.
In the fish center-of-mass coordinate system, the swimming velocity of the fish u, can be decomposed into the translational velocity uc, the rotation velocity Ω, and the deformation velocity u′:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_{\rm{c}}} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{r'}} + \mathit{\boldsymbol{u'}}, $ | (8) |
where r′ is the coordinate of the fish body in the center-of-mass reference system. The deformation satisfies the linear and angular momentum conservation laws
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\int {\rho \mathit{\boldsymbol{u'}}{\rm{d}}V} = 0, $ | (9a) |
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\int {\rho \mathit{\boldsymbol{r'}}} \times \mathit{\boldsymbol{u'}}{\rm{d}}V = 0. $ | (9b) |
What Fig. 3(a), 3(b) shows is under the head system. To satisfy Eq. (9), it should be transformed into the center-of-mass system, as shown in Fig. 3(c). The rotational angle of the center-of-mass reference system relative to the head system is computed using Newton's iteration method according to Eq. (9b). The deformation speed is determined by the deformation under the center-of-mass system. The translation and rotation of the fish body are governed by Newton's second law of motion
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {m{\mathit{\boldsymbol{u}}_{\rm{c}}}} \right) = \mathit{\boldsymbol{F}}, $ | (10a) |
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {I\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right) = \mathit{\boldsymbol{M}}, $ | (10b) |
where m=∫ρdV is the mass, I=∫ρ(r′·r′)dV is the moment of inertial (due to the deformation of the fish, the moment of inertia changes with time), F=∮(
The finite-volume method, artificial compression, and overlapping grids were used to solve the hydrodynamic equations. The Newton iteration method was used to couple the hydrodynamics and the deforming body dynamics. Those methods have been verified and validated, and has been used in the study of fishlike C-escape[11].
1.5 Dimensionless parametersIn the experiment shown in Fig. 1, the fish body length is L=3.31 cm, the duration of the C-turn is Tturn=145.6 ms, and the duration of the C-escape is Tescape=53.4 ms. Take L and Tescape as the characteristic length and time, then the characteristic velocity is U=L/Tescape=0.62 m/s, the Reynolds number is Re=UL/ν=2.05×104, and the dimensionless duration of C-turn is 2.73. Where ν=1.003 ×10-6 m2/s is the kinematic viscosity coefficient of water. According to the two-dimensional fish body model defined by Eq. (1), dimensionless fish mass and initial moment of inertia are 6.36×10-2 and 4.01×10-3, respectively.
To measure hydrodynamic and energetics properties, we define the thrust, torque, and power coefficients as follows:
| $ {C_{\rm{T}}} = \frac{{\mathit{\boldsymbol{F}} \cdot {\mathit{\boldsymbol{u}}_{\rm{c}}}/\left| {{\mathit{\boldsymbol{u}}_{\rm{c}}}} \right|}}{{0.5\rho {U^2}L}},{C_{\rm{M}}} = \frac{{\mathit{\boldsymbol{M}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}/\left| \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \right|}}{{0.5\rho {U^2}{L^2}}}, $ |
| $ {C_{\rm{P}}} = \frac{{{\rm{Power}}}}{{0.5\rho {U^3}L}},{C_{\rm{E}}} = \frac{{{\rm{Energy}}}}{{0.5\rho {U^2}{L^2}}}. $ |
Where thrust is the component of the fluid force along the direction of the fish movement, the sign of the torque indicates whether it is in the same direction with the angular speed, and Power is the mechanical power consumed during the fish's self-propelled swimming, which is defined as
| $ {\rm{Power}} = \oint { - \left( {\tilde \sigma \cdot \mathit{\boldsymbol{n}}} \right) \cdot \mathit{\boldsymbol{u'}}{\rm{d}}S} + \frac{{\rm{d}}}{{{\rm{d}}t}}\int {\frac{1}{2}\rho {{\left| {\mathit{\boldsymbol{u'}}} \right|}^2}{\rm{d}}V} . $ | (11) |
It is related to the deformation velocity, including the power needed by the deforming body to overcome the fluid force and to change the deformation kinetic energy, according to the energetics analysis in Ref.[23]. Mechanical energy consumption is Energy=
Both thedeformation and duration of C-turns and C-escapes are different. In order to explore their effects separately, we investigated four cases, as shown in Table 3. Case1 and case3 are the C-turn and C-escape of zebrafish in the experiment shown in Fig. 1. Case2 and case4 have the same deformation with case1 and case2, respectively, but the duration is different.
|
|
Table 3 The setups and numerical simulation results of the four cases |
We use the velocity ue and turning angle θe of the end time to measure the acceleration and turning performance of C-start, and define the relative propulsion efficiency η′u=ηu/ηumax and relative turning efficiency η′θ=ηθ/ηθmax. Where ηu=ue/CE and ηθ=θe/CE denote the ratio between velocity and energy, and the ratio between turning angle and energy, respectively. ηumax and ηθmax are the largest value among the four cases. The results are listed in Table 3 and will be discussed below.
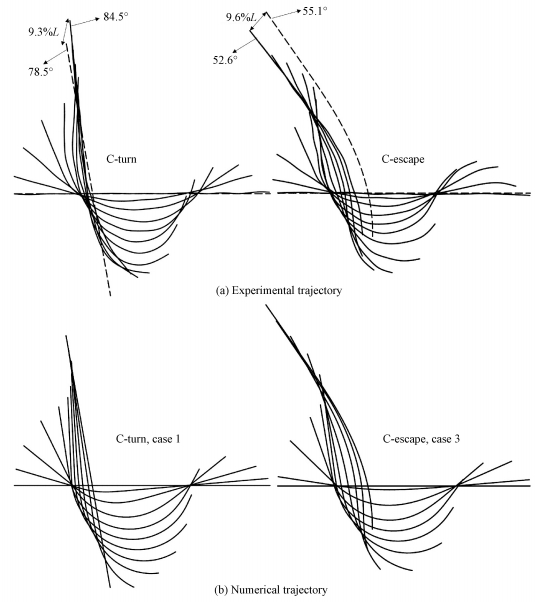
2.1 Numerical simulation results and comparisons with experimentFigure 4 shows the trajectory of the fish midline of C-turn (case 1) and C-escape (case 3) obtained from experiments and numerical simulations. We use the position and angle of the fish head of the end moment to represent errors between numerical simulations and experiments. In Fig. 4(a), the dashed line is the fish midline of numerical simulation, and the black line is that of experiment. It can be seen that the head position error of C-turn is 9.3%, the turning angle error is 7.1% (1-78.5/84.5), and the position error of C-escape is 9.6%, the angle error is 4.8% (55.1/52.6-1). All the error was lower than 10%. Because what we used in this paper was a two-dimensional and uniform density fish model, and the pectoral and caudal fins, three-dimensional fish body and flow field, and the density distribution was not taken into consideration, the error within 10% is acceptable. Overall, numerical simulations were basically consistent with experiments, which reflected the kinematics characteristics of C-turns and C-escapes.
|
Download:
|
|
Fig. 4 Comparison of the fish midline trajectory between the experiment and numerical simulation |
|
Table 3 demonstrates that, case1 has the lowest energy consumption and the highest relative propulsion efficiency and relative turning efficiency, while case 3 achieves the fastest swimming velocity. They have different deformation and duration, whose influence will be discussed separately in the succeeding sections.
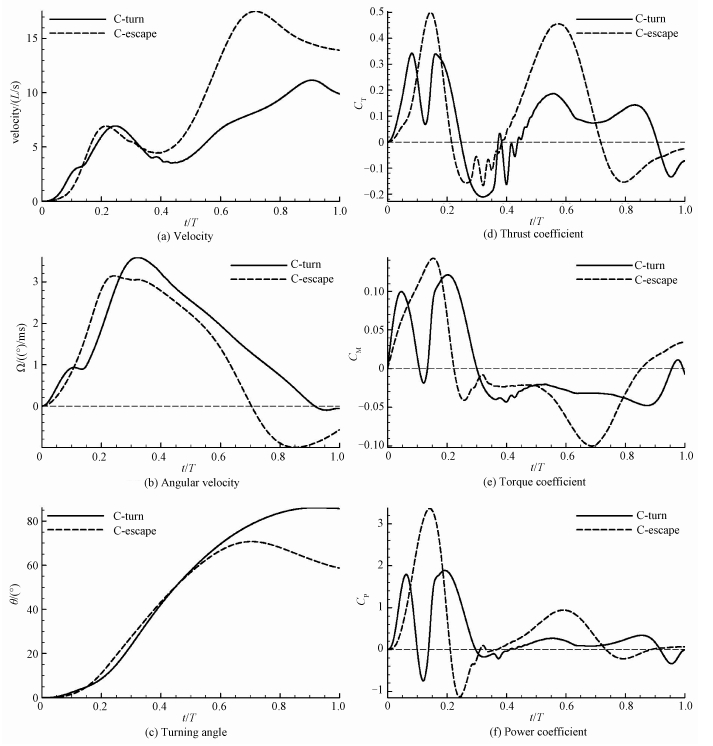
2.2 Effects of deformation patternsC-turn (case 2) and C-escape (case 3) are numerically simulated with the same duration (53.4 ms). As shown in Table 3, C-turn still have greater turning angles and lower energy consumption than C-escape, even with the same duration. Figure 5 displays the time curves of the velocity, angular velocity, turning angle, thrust coefficient, torque coefficient and power coefficient of C-turn (case 2) and C-escape (case 3). According to the definition in Fig. 3, t/T=0-0.4 is the bending phase (stage 1), and t/T=0.4-1 is the backward flapping phase (stage 2).
|
Download:
|
|
Fig. 5 Time curves of C-turn (case 2) and C-escape (case 3) |
|
Figure 5 (a) shows that velocity of C-turn and C-escape is very close at stage 1. After t/T=0.4, velocity of C-escape increase rapidly, peak at around t/T=0.7 (17.5L/s), and then decline slightly. However, the velocity enhancement of C-turn is not as significant as C-escape, whose peak value is 11.2L/s at around t/T=0.9. At the end time, the speed of C-escape (13.9L/s) is 40.4% higher than that of C-turn (9.9L/s). The difference in speed is due to the thrust of the fluid. It can be seen from Fig. 5 (d), both the thrust coefficients of C-turn and C-escape peak at about t/T=0.57 in stage 2. The peak of the C-escape (0.46) is 2.4 times that of the C-turn (0.19).
As shown in Fig. 5 (e), both the torque coefficients of C-turn and C-escape present positive torque at first and then negative torque. Positive torque has a large number and last a short time, however negtive torque has a relative little number and last a long time. This leads the angular velocity in Fig. 5 (b) to raise rapidly first and then decrease slowly. Time integration of the angular velocity results in the change of turning angle in Fig. 5 (c). Although the positive torque peak of C-turn (0.12) is slightly lower than C-escape (0.14), the duration of positive torque of C-turn (t/T=0-0.3) is longer than C-escape (t/T=0-0.22), which result that C-turn has a greater peak angular velocity (3.6(°)/ms) than C-escape (3.1(°)/ms). On the other hand, C-escape has a larger negative torque peak (-0.1) than C-turn (-0.048), which results that the angular velocity of C-turn decline slowly and almost stays positive all the time, however the angular velocity of C-escape fall quickly and reduce to negative at t/T=0.7. So the turning angle of C-turn increase constantly, while the turning angle of C-escape begins to decrease at t/T=0.7. Figure 5 (c) shows that the gap of turning angle between C-turn and C-escape expands after t/T=0.7. At last, the turning angle of C-turn (85.7°) is 46% larger than C-escape (58.7°).
Figure 5 (f) shows that the peak power coefficient at stage 1 is much larger than stage 2. Integrate the power coefficient, we could see that the energy consumed by C-turn and C-escape at stage 1 account for 77% and 63% of the total energy, respectively. This indicates that energy is mainly consumed at stage 1 in C-start, especially in C-turn. On the other hand, both the peak power coefficient of C-escape at stage 1 and stage 2 are larger than C-turn. At stage 1 the peak power coefficient of C-escape (3.36) is 1.78 times that of C-turn (1.89), and at stage 2 the peak power coefficient of C-escape (0.94) is 2.76 times that of C-turn (0.34).
In addition, we found that there were two peaks in each curve of C-turn at stage 1. This is due to the two mechanismsof C-bend: curvature growth and propagation, as shown in the curvature-time model in Fig. 2 (b). The twin peaks in the time curves of C-turn reflect the curvature growth and curvature propagation, respectively. Parameter ta indicates the speed of curvature growth. ta=0.15T, 0.3T for C-turn and C-escape, respectively, as shown in Table 2. Due to ta of C-turn is small, before the curvature of the C-turn begin to propagate, it has reached a peak. However, ta of C-escape is large, so when the curvature starts to propagate, it's still increasing, and the growth and spread of curvature overlap with each other.
In order to further understand the hydrodynamics and energetics mechanism of C-turns and C-escapes, we ploted the vorticity of the flow field, the center-of-mass reference system and the fluid stress distribution in Fig. 6. Since the Reynolds number in this paper is 2.05×104, so the viscous stress is much smaller than the pressure stress and we only show the pressure distribution. The pressure on the two sides of the fish was concentrated to the midline, and the length of the arrow indicates the relative magnitude of the pressure.

|
Download:
|
|
Fig. 6 The vorticity field, the fluid stress distribution, and the center-of-mass frame |
|
As was stated above, we decomposed the fish swimming into translation, rotation and deformation. The translation and rotation is the motion of the center-of-mass coordinate system in Fig. 6, and the deformation is under the center-of-mass system, which is exactly the same with that in Fig. 3(c). The so-called self-propelled numerical simulation is to determine the acceleration and angular acceleration of the fish body, and then the velocity, angular velocity, position and angle of the center-of-mass system, according to the fluid force and torque, at the given predetermined deformation under the center-of-mass system.
Figure 6 demonstrates that C-turn and C-escape have similar flow field. At stage 1, a positive vortex sheds from the head and a negative vortex sheds from the tail. At stage 2, another positive vortex sheds from the tail. However, due to the reversed bending at stage 2 of C-escape, a negative vortex generates at t/T=0.9 near to the tail. Moreover, the positive vortex of C-escape near to the tail is stronger than that of C-turn (for example, t/T=0.5, 0.6), and the time of shedding is earlier. The positive vortex sheds from the tail completely at t/T=0.8 in C-escape, while at the end time in C-turn. The vortex will result in the generation of jet in the flow field, which will induce the fluid force and torque on the fish.
In Fig. 5(f), power coefficient peaks at t/T=0.2 in C-turn, and at t/T=0.1 in C-escape. Form Fig. 6 we found that the fluid stress also peaks at t/T=0.2 and 0.1 in C-turn and C-escape, respectively. This indicates that the power at stage 1 is mainly used to overcome the fluid stress generated by the C-shaped bending. At stage 1, there are three alternating reversed fluid stress on the head, the middle of the fish body, and the tail. At t/T=0-0.4 in C-turn and t/T=0-0.2 in C-escape, the stress on the head causes a negative torque and the stress on the tail causes a positive torque. Although the stress on the head is greater, the range of stress on the tail is larger, and the tail is further away from the center-of-mass so the arm of force is longer. The positive torque on the tail will overcome the negative torque on the head, and the fish will subject to a positive torque overall. However, at t/T=0.5-0.8 in C-turn and t/T=0.3-0.7 in C-escape, the direction of stress will reverse. The stress on the head will generate a positive torque and the stress on the tail will generate a negative torque, and the negative torque at the tail will dominate for the same reason as above. The thrust coefficient of C-escape peaks at t/T=0.6 in Fig. 5(d), and the stress on the tail also reaches the peak of stage 2 and along the direction of body movement. The stress peak at stage 2 of C-escape is greater than C-turn, which leads to a large enhancement of the velocity in C-escape. However, the larger stress will generate a larger negative torque. At t/T=0.7, the stress on the tail in C-escape is almost perpendicular to the body, so the arm of force is large, and the negative torque reaches a peak. However, the stress on the tail in C-turn is smaller and the arm is short, so the negative torque of C-turn is smaller than C-escape.
The Strouhal numbers (St=A/uT) in fish steady swimming is in the range of 0.25-0.35, where A is the width of the wake. In zebrafish C-start, we define A as the amplitude of the tail's deformation in the center-of-mass frame, as shown in Fig. 3(c). Then the Strouhal number of C-turn and C-escape is 0.59 and 0.57, respectively, as listed in Table 4. Such Strouhal numbers are very high, which will induce a sharp thrust and a low propulsive efficiency. Strouhal numbers of C-turn and C-escape have little difference, and the velocity is proportional to the amplitude of the tail. This indicates that due to the reverse bending in C-escape the deformation amplitude of tail increases, and the velocity will increase accordingly.
|
|
Table 4 Strouhal numbers of C-turn and C-escape |
The effect of duration on the velocity, the turning angle and the energy consumption of C-turn and C-escape were studied in this section.
Table 3 shows that, if the duration of C-turn increase from 53.4 ms (case 2) to 145.6 ms (case 1), the swimming velocity will reduce by 69% (1-3.1/9.9), but the energy consumption can reduce by 86% (1-4.47/32.9), and the turning angle only reduce by 8% (1-78.5/85.7). However, if the duration of C-escape decrease from 145.6 ms (case 4) to 53.4 ms (case 3), the energy consumption will increase by 6.3 times (46.9/6.44-1), swimming velocity will increase by 2.2 times (13.9/4.3-1), and the turning angle only increase by 10% (58.7/53.3-1). This demonstrates that the duration has little effect on the turning angle, but has a significant effect on the velocity and energy consumption. Increasing duration of C-turn can significantly reduce energy consumption, and decreasing duration of C-escape can greatly increase the velocity. The reason may be that the turning angle is a dimensionless quantity, but the dimension of velocity (L/T) is proportional to the reciprocal of time and the dimension of energy consumption (ρL4/T2) is proportional to the square of time's reciprocal.
By comparing the four cases in Table 3, we find that the C-turn in reality (case 1) consumes the least amount of energy, and its relative propulsion and turning efficiency are the highest, but it has the slowest swimming velocity. However, the C-escape in reality (case 3) has the fastest swimming velocity, but meanwhile it consumes the most energy, and the relative propulsion and turning efficiency are the lowest. Moreover, the highest turning angle is in case 2, and the second is case1. This indicates that zebrafish pursues relatively high turning angles and to save energy in C-turn, while pursues the fastest swimming velocity at the cost of high energy consumption in C-escape.
3 ConclusionIn conclusion, we established models of zebrafish's C-turn and C-escape. Parameters were derived with an optimization algorithm according to the experimental data. The deformation obtained by the curvature model accorded with the experiment very well. We performed self-propelled numerical simulation, and the patterns of the midline of fish was also consistent with experiment(the error was within 10%).
By comparing C-turn and C-escape models, there are three points worth noting. Firstly, the difference in swimming velocity and turning angle between the C-turn and C-escape mainly occurred at stage 2. Secondly, the mechanism of the turning was that a large positive torque was generated at stage 1 and a relative small reverse torque was generated at stage 2, which led to the positive angular velocity to maintain for a long period of time and to obtain turning angle. Furthermore, the reverse bending of C-escape at stage 2 increased the tail's deformation amplitude, resulting in a strong fluid stress and a high velocity. Meanwhile, the reverse bending also led to the negative torque to increase, which resulted in that the angular velocity decreased rapidly and the turning angle reduced.
We conclude that the duration had little effect on the turning angle, but had a significant influence on the swimming speed and energy consumption. Improving the duration of C-turn significantly reduced the energy consumption and maintained a relatively high turning angle at the same time. Decreasing the duration of C-escape dramatically increased the swimming velocity, but it required much more energy.
In fact, fishes need to adjust their turning angles and the swimming velocity to perform various swimming behavior, and fishes have different shapes in general. In the future, we will study the impact of different curvature model parameters and fish shapes on the performance of C-start.
Supplementary material: Original experimental images and animations of numerical simulation are available at https://pan.baidu.com/s/1TlOU3_-ycWdqdtXIUeBAVw.
The authors thank Zhang Bingbing for providing zebrafish experimental images.
| [1] |
Domenici P, Blake R. The kinematics and performance of fish fast-start swimming[J]. Journal of Experimental Biology, 1997, 200(8): 1165-1178. |
| [2] |
Triantafyllou M S. Survival hydrodynamics[J]. Journal of Fluid Mechanics, 2012, 698: 1-4. DOI:10.1017/jfm.2012.82 |
| [3] |
Domenici P, Blake R W. The kinematics and performance of the escape response in the angelfish (Pterophyllum eimekei)[J]. Journal of Experimental Biology, 1991, 156(1): 187-205. |
| [4] |
Harper D G, Blake R W. Fast-start performance of rainbow trout Salmo gairdneri and northern pike Esox lucius[J]. Journal of Experimental Biology, 1990, 150(1): 321-342. |
| [5] |
Zhang B B, Yu Y L. Living body experimental study of dynamic characteristics of zebrafish C-start swimming[J]. Journal of Expermental Mechanics, 2014, 29(6): 727-736. |
| [6] |
Hu W R, Yu Y L, Tong B G, et al. A numerical and analytical study on a tail-flapping model for fish fast C-start[J]. Acta Mechanica Sinica, 2004, 20(1): 16-23. DOI:10.1007/BF02493567 |
| [7] |
Jing J, Yin X Z, Lu X Y. Hydrodynamic analysis of C-start in crucian carp[J]. Journal of Bionic Engineering, 2004, 1(2): 102-107. DOI:10.1007/BF03399460 |
| [8] |
Jing J, Yin X Z, Lu X Y. Observation and hydrodynamic analysis of fast-start of yellow catfish (Pelteobagrus fulvidraco)[J]. Progress in Natural Science, 2005, 15(1): 34-40. DOI:10.1080/10020070512331341740 |
| [9] |
Tytell E D, Lauder G V. Hydrodynamics of the escape response in bluegill sunfish, Lepomis macrochirus[J]. Journal of Experimental Biology, 2008, 211(21): 3359-3369. DOI:10.1242/jeb.020917 |
| [10] |
Witt W C, Wen L, Lauder G V. Hydrodynamics of C-start escape responses of fish as studied with simple physical models[J]. Integrative and comparative biology, 2015, 55(4): 728-739. DOI:10.1093/icb/icv016 |
| [11] |
Liu G, Yu Y L, Tong B G. Flow control by means of a traveling curvature wave in fishlike escape responses[J]. Physical Review E, 2011, 84(5): 56312. DOI:10.1103/PhysRevE.84.056312 |
| [12] |
Gazzola M, Van Rees W M, Koumoutsakos P. C-start:optimal start of larval fish[J]. Journal of Fluid Mechanics, 2012, 698: 5-18. DOI:10.1017/jfm.2011.558 |
| [13] |
Li G, Müller U K, Van Leeuwen J L, et al. Body dynamics and hydrodynamics of swimming fish larvae:a computational study[J]. Journal of Experimental Biology, 2012, 215(22): 4015-4033. DOI:10.1242/jeb.071837 |
| [14] |
Li G, Müller U K, Van Leeuwen J L, et al. Escape trajectories are deflected when fish larvae intercept their own C-start wake[J]. Journal of The Royal Society Interface, 2014, 11(101): 20140848. DOI:10.1098/rsif.2014.0848 |
| [15] |
Borazjani I, Sotiropoulos F, Tytell E D, et al. Hydrodynamics of the bluegill sunfish C-start escape response:three-dimensional simulations and comparison with experimental data[J]. Journal of Experimental Biology, 2012, 215(4): 671-684. DOI:10.1242/jeb.063016 |
| [16] |
Borazjani I. The functional role of caudal and anal/dorsal fins during the C-start of a bluegill sunfish[J]. Journal of Experimental Biology, 2013, 216(9): 1658-1669. DOI:10.1242/jeb.079434 |
| [17] |
Song J L, Zhong Y, Luo H X, et al. Hydrodynamics of larval fish quick turning: a computational study[J/OL]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, (2017-12-01)[2018-03-05]. http://journals.sagepub.com/doi/10.1177/0954406217743271. DOI: 10.1177/0954406217743271.
|
| [18] |
Carling J, Williams T L, Bowtell G. Self-propelled anguilliform swimming:simultaneous solution of the two-dimensional Navier-Stokes equations and Newton's laws of motion[J]. Journal of experimental biology, 1998, 201(23): 3143-3166. |
| [19] |
Kern S, Koumoutsakos P. Simulations of optimized anguilliform swimming[J]. Journal of Experimental Biology, 2006, 209(24): 4841-4857. DOI:10.1242/jeb.02526 |
| [20] |
Xin Z Q, Wu C J. Numerical simulations and vorticity dynamics of self-propelled swimming of 3D bionic fish[J]. Science China:Physics, Mechanics & Astronomy, 2012, 55(2): 272-283. |
| [21] |
Su Z S, Yu J Z, Tan M, et al. Implementing flexible and fast turning maneuvers of a multijoint robotic fish[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(1): 329-338. |
| [22] |
Yang Y, Wu G H, Yu Y L, et al. Two-dimensional self-propelled fish motion in medium:an integrated method for deforming body dynamics and unsteady fluid dynamics[J]. Chinese Physics Letters, 2008, 25(2): 597-600. DOI:10.1088/0256-307X/25/2/066 |
| [23] |
Wang Z W, Yu Y L, Tong B G. An energetics analysis of fish self-propelled swimming[J]. Science China:Physics, Mechanics & Astronomy, 2018, 61(7): 74721. |
 2019, Vol. 36
2019, Vol. 36 


