2. 青岛海洋科学与技术国家实验室, 山东 青岛 266237
2. Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237, Shandong, China
自进入21世纪以来,科技的发展使得人们能够更好地认知海洋与开发海洋资源。拥有广阔领海的中国有着丰富的海洋资源,大陆海岸线长约18 000 km,海域面积达470万km2,海洋生物资源、近岸的潮汐能、南海的海上石油资源等都能有效缓解中国在陆地能源短缺方面的问题[1]。同时中国海洋科学研究的逐渐兴起对海事预警、港口减灾、海域作业安全等方面做出了很大贡献,进一步促进了海洋资源的利用。其中如何有效利用近岸海域资源仍是人们关心的主要问题,这要求我们对近岸复杂的水动力环境投入大量研究,而准确模拟水波在近岸区域的非线性特性则是其中重要课题之一,并具有非常重要的学术价值和工程意义。
海啸波传播至浅水区域时,水波的非线性会发生明显变化。海底坡度变陡、海底粗糙程度升高等因素使得波动的非线性程度迅速升高,这时的波高情况与线性浅水方程的模拟结果可能会有较大出入。Satake[2]利用线性和非线性浅水波方程模拟1992年Nicaragua地震引发的海啸,发现线性系统会过高估计海啸波高,尤其是在波幅变大的浅水区域;而非线性系统又会低估海啸爬高的高度。在中国海域的海啸预警中,已有研究证明海啸波传播至中国近岸海域(如海南岛附近[3]、长江三角洲[4]、东部沿海[5]、渤海地区[6])时具有明显的非线性特征。王培涛等[7]研究线性和非线性浅水波方程在南海和东海区的适用性。他们分别考虑了海啸首波及后续波波幅,结果表明在水深小于100 m的南海近岸区域,首波差别不大,所以在不考虑海啸爬高作用时,用线性系统就可以满足海啸预警需求;而在水深小于100 m的东海近岸区,因首波和后续波波幅差别都较大,所以必须考虑海啸非线性作用。Liu等[8]同样证实在南海区域可以使用线性系统研究海啸波传播,而东海区域的非线性效应不可忽略。
而在研究近岸其他水波问题,如浅海风暴潮、天文潮、波生流时,其水波表现就是由于源项的非线性,若将非线性效应(如底摩擦项、浅水效应项、对流项)都略去,则对应的特征波动状态消失[9]。这类波多是深水波,对其的非线性研究需要根据实际水波的非线性程度选取控制方程的非线性程度。
无论是利用理论分析还是数值计算研究近岸水波问题,都需要用偏微分方程描述相应的物理过程,即进行数学建模。同时,物理观测也常需要偏微分方程进一步分析或验证结论[10]。本文在非线性特性分类的基础上,对基础水波动力学方程进行探讨,分析各个方程的非线性程度及其适用的物理问题。
1 近岸非线性水波基础理论及控制方程现今利用偏微分方程模拟近岸波浪的动力特性主要有两种方法。第一种是通过用水深积分、水深平均或任意水深处的速度表示垂向速度,使得三维方程降为二维,大大简便数值模拟计算,如利用二维完全非线性Boussinesq模型研究近岸波浪与水流相互作用[11];第二种是利用非线性方程描述整个波浪场,利用不同的非线性项表示不同的非线性场景,如利用VOF方法研究孤立波与防波堤之间的交互作用[12]。
最简单的水波非线性传播过程可表示为
| $ \frac{{\partial \zeta }}{{\partial t}} + {C_0}\frac{{\partial \zeta }}{{\partial x}} + \kappa \zeta \frac{{\partial \zeta }}{{\partial x}} = 0, $ | (1) |
式中:κ是非线性系数,ζ为总水深。在运动坐标系X=x-C0t中,式(1)归结为Hopf方程的标准型:
| $ \frac{{\partial \zeta }}{{\partial t}} + \kappa \zeta \frac{{\partial \zeta }}{{\partial x}} = 0. $ | (2) |
一般情况下,对于给定的初始条件
| $ \zeta = f\left( x \right), $ | (3) |
方程(1)的解可用含参数的函数表示为
| $ \left\{ \begin{array}{l} x = \xi + \left[ {{C_0} + \kappa f\left( \xi \right)} \right]t\\ \zeta = f\left( \xi \right) \end{array} \right., $ | (4) |
或用隐函数的形式表示为
| $ \zeta = f\left[ {x - \left( {{C_0} + \kappa \zeta } \right)t} \right]. $ | (5) |
当水波传播具备非线性效应时,也就是κ不等于零时,上述解的叠加原理不再成立。
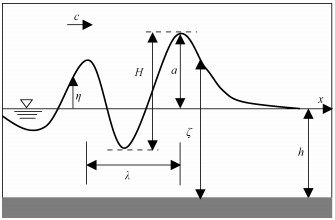
水波传播时垂向上的参数(水深、波幅、波高等,如图 1所示)可作为水波非线性程度分类的依据,Zweifel等[13]基于初始波的波幅与波高之比刻画水波偏离静面的程度:
|
Download:
|
| c为波传播速度,η为自由水面,H为波高,a为振幅,λ为波长,h为静水水深,ζ为总水深。 图 1 近岸水波波动场示意图 Fig. 1 Geometry of nearshore water wave field | |
| $ 0.9 < {a_1}/{H_1} \le 1.0,强非线性, $ | (6) |
| $ 0.6 < {a_1}/{H_1} \le 0.9,中等非线性, $ | (7) |
| $ 0.4 < {a_1}/{H_1} \le 0.6,弱非线性. $ | (8) |
式中:a1表示初始冲击波的波幅,H1表示初始冲击波的波高(初始波的波峰与波谷之差),不等式两端的允许偏差均为±10%。在实际水波中,初始波波幅常为最大波幅,且远大于接下来的后续波幅[14],所以a1/H1 < 0.4的情况未被观测到。同时,a1/H1=1.0的情况也不会在自然界发生,因为自然界中不会产生纯孤立波[15]。
另一种给水波非线性分类的方法[10]则是利用有限振幅波Stokes理论中的参数波陡
| $ \theta = H/\lambda , $ | (9) |
式中:θ是水波的波陡,H是波高,λ是波长。波陡表征水波的斜率,在有限振幅波Stokes理论中,极限状体下波峰处波面夹角等于2π/3,得出波陡具有极限值0.142,当大于该值时,波面发生破碎。该分类方法认为在推导近岸水波方程过程中,当波陡只保留0阶近似时,对应的水波不具备非线性特性,而适应线性理论;保留至波陡的1阶小量时,则为弱非线性;若波陡保留至2阶或2阶以上小量时,则为强非线性理论。
波浪的非线性的特征为波峰变陡,波谷趋于平坦,这体现了不对称性,而这种不对称性直接影响波浪的轨道速度,使得轨道速度也有一定的不对称性。前人基于这类不对称性提出倾斜指数,以此作为水波的非线性指标。常见的倾斜指数[16]可用轨道速度、轨道速度的加速度或周期来表示:
| $ {R_{\rm{u}}} = \frac{{{u_{\max }}}}{{{u_{\max }} - {u_{\min }}}}, $ | (10) |
| $ {R_{\rm{a}}} = \frac{{{a_{\max }}}}{{{a_{\max }} - {a_{\min }}}}, $ | (11) |
| $ {R_{\rm{T}}} = \frac{{T - 2{T_{{\rm{fwd}}}}}}{T}. $ | (12) |
式中:umax、amax分别是正向最大速度及最大加速度;umin、amin分别是反向最大速度及最大加速度;T是水波运动的周期;Tfwd是前倾波在正向运动中波速上升阶段零点和波峰之间的时间;Ru、Ra、RT分别为速度倾斜指数、加速度倾斜指数、周期倾斜指数。基于大量近岸波浪的实际观测和分析,非线性指标的范围为0.51≤Ru≤0.66,0.46≤RT≤0.78,这表示在近岸水动力环境中,非线性是普遍存在且显著的[17]。基于以上倾斜指数也可对近岸非线性程度进行分类。
上述几种分类适用于对物理实验观测(如U型振荡水槽)中的平面波进行特性分析,而在近岸海域、港湾港口中分析水波,常用Stoker[18]提出的波幅与水深之比(相对水深)反映非线性效应:
| $ \alpha = a/h, $ | (13) |
式中:a是水波的波辐,h是水深,α是波的非线性效应参数。而对于不同的近岸场景或水波现象,非线性水波对应的尺度与参数是复杂多样的,同时水波的频散性具有减缓甚至抵消非线性效应的作用,所以研究近岸水波非线性特性时常加入频散效应参数来辅助分析:
| $ \varepsilon = {h^2}/{\lambda ^2}, $ | (14) |
式中:λ是水波的波长,ε指示波的频散效应参数。
考虑了频散效应的水波非线性传播过程可用方程(1)加入三阶导的频散项来表示,即KdV方程
| $ \begin{array}{l} \frac{{\partial \zeta }}{{\partial t}} + {C_0}\frac{{\partial \zeta }}{{\partial x}} + \kappa \zeta \frac{{\partial \zeta }}{{\partial x}} + \mu \frac{{\partial {\zeta ^3}}}{{\partial {x^3}}} = 0. \end{array} $ | (15) |
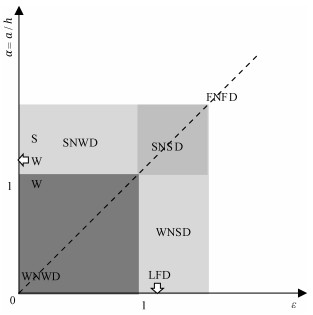
根据两个参数可将现有的近岸非线性水波模型进行分类,见图 2。
|
Download:
|
| 图 2 根据非线性效应和频散效应的非线性水波模型分类 Fig. 2 Classification of nonlinear water wave models based on nonlinearity and dispersion | |
图 2中的弱频散性(WD)表示对应的理论或模型只在频散效应参数较小的情况下才能较好地近似真实水波;如果理论或模型在频散效应参数较大的条件下都能良好地近似真实水波的频散性,则称该理论或模型是强频散性(SD)的。
2 近岸弱非线性模型及适用现象弱非线性水波问题主要有洪水波模拟[19]、潮汐波爬坡问题[20]、海啸波传播与上岸[4, 21-29, 30],沿岸流不稳定演化问题[31-34],常用的方程有浅水波方程、低阶Boussinesq方程、经典的Hamilton正则方程。
2.1 浅水波方程多数近岸海域的重要特征就是海底坡度较小,这决定了近岸水波特征量的空间变化一般都是平缓过程。在浅水条件下,水波运动引起的流动在垂直方向上的加速度可以忽略不计,假设波动场中压强在垂直方向上满足静水压分布规律,由此可认为水平流速在垂直方向上的分布是接近均匀的,利用这一条件可将三维问题降为二维问题,若不考虑频散效应,则可用浅水波方程或长波方程描述水波运动,用参数表示为α=Ο(1), ε=0,浅水波方程的标准形式为:
| $ \frac{{\partial \zeta }}{{\partial t}} + \mathit{\boldsymbol{\bar u}} \cdot \bar \nabla \zeta + \zeta \bar \nabla \cdot \mathit{\boldsymbol{\bar u}} = 0, $ | (16) |
| $ \frac{{\partial \bar u}}{{\partial t}} + \left( {\mathit{\boldsymbol{\bar u}}\bar \nabla } \right)\mathit{\boldsymbol{\bar u}} + g\bar \nabla \zeta = g\bar \nabla h. $ | (17) |
式(16)和式(17)构成一组关于瞬时总水深ζ和垂线平均流速
鉴于浅水波方程的非线性项阶数低,非线性弱,且完全忽略水波的频散特性,所以经典浅水波方程属于图 2中纵轴上的经典非线性浅水波区shallow water wave (SWW)区。潮汐波、海啸波、洪水波等近岸水波问题符合SWW区域的参数条件,因此常用浅水波方程分析和解决此类问题。
Monnier等[19]利用二维浅水波方程精确模拟洪水涌入干燥近岸陆地的场景,并利用真实的地理情况(莱兹河的洪水平原)模拟历史上的真实洪水波上岸。该洪水波模型具有动态干湿前缘,并且在浅水波方程中加入非线性低摩擦项,以此精确分析非平坦河床的摩擦作用对洪水波非线性作用的贡献,结果表明弱非线性无频散性的经典浅水波方程适用于模拟近岸洪水波上岸。现今大量的海啸模型都是基于经典非线性浅水波方程进行海啸预警及海啸灾害评估,如美国NOAA/PMEL的Titov和美国南加州大学Synolakis开发的MOST模型[21]即是利用球坐标下的二维非线性浅水波方程模拟海啸传播过程,日本Tohoku大学开发的TUNAMI模型[22]利用加入摩擦项的非线性浅水波方程构建近岸海啸预警系统,由Arcos和Leveque开发的CLAWPACK程序包[27]则是利用非线性浅水波方程的保守形式作为海啸传播和上岸的控制方程。上述3个模型被大量的科研人员应用于海啸模拟并利用验潮站实时数据加以验证[4, 24-26, 29],已经成为近岸海啸波模拟的成熟模型。弱非线性的浅水波方程也被应用于分析在小波幅波浪范围内的沿岸流非线性不稳定演化问题[31-33]。近期的相关工作如沈良朵[34]在非线性浅水波方程中加入波浪驱动力项、侧向混合项(或称涡旋项)、底摩擦项,3项均为弱非线性,且其中的侧向混合项可对应求得涡量场,以此分析沿岸流的非线性特征。
如今,浅水波方程模拟近岸水波的进展方向是将静水压条件改为非静水压条件,由此可以解决经典浅水波无法模拟某些水波色散特性的问题(如不同频率的水波以不同速度传播的问题),这在一定程度上弥补了经典浅水理论中完全忽略频散性的问题。如Le等[20]保留垂直方向上的动量方程,并利用水底面与水表面的平均值求得垂直方向的潮汐波速度,模拟越南岘港湾的潮汐事件。Aricoò和Re[30]则更加细化非静压的非线性浅水波数值模型,将对流加速度非线性项加入到垂向上的动量方程中,并利用该模型模拟在不规则地形上的海啸波爬坡的过程。
2.2 经典的Boussinesq方程虽然浅水波方程能够有效模拟近岸的一些弱非线性的水波现象,但仍然无法满足频散作用显著的情况,只适用于水深极小的情况或频率极低的水波。在实际近岸问题中,水波除受非线性作用,还要受到频散性的影响。最先考虑频散性的工作来自Boussinesq[35],对应的方程即为Boussinesq方程。
| $ \frac{{\partial \eta }}{{\partial t}} + \frac{{\partial \left[ {\left( {h + \eta } \right)u} \right]}}{{\partial x}} + \frac{{\partial \left[ {\left( {h + \eta } \right)u} \right]}}{{\partial y}} = 0, $ | (18) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + g\frac{{\partial \eta }}{{\partial x}} = }\\ {\frac{1}{2}h\left[ {\frac{{{\partial ^3}\left( {hu} \right)}}{{{\partial ^2}x\partial t}} + \frac{{{\partial ^3}\left( {hv} \right)}}{{\partial x\partial y\partial t}}} \right] + }\\ {\frac{1}{6}{h^2}\left[ {\frac{{{\partial ^3}u}}{{{\partial ^2}x\partial t}} + \frac{{{\partial ^3}v}}{{\partial x\partial y\partial t}}} \right],} \end{array} $ | (19) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial v}}{{\partial t}} + v\frac{{\partial v}}{{\partial y}} + u\frac{{\partial v}}{{\partial x}} + g\frac{{\partial \eta }}{{\partial x}} = }\\ {\frac{1}{2}h\left[ {\frac{{{\partial ^3}\left( {hv} \right)}}{{{\partial ^2}y\partial t}} + \frac{{{\partial ^3}\left( {hu} \right)}}{{\partial x\partial y\partial t}}} \right] + }\\ {\frac{1}{6}{h^2}\left[ {\frac{{{\partial ^3}v}}{{{\partial ^2}y\partial t}} + \frac{{{\partial ^3}u}}{{\partial x\partial y\partial t}}} \right].} \end{array} $ | (20) |
式中:u(x, y, t)和v(x, y, t)分别表示水平方向x、y上的水深平均水平速度;h为静水水位;η为瞬时波面。
经典Boussinesq方程属于图 2中的weakly nonlinear and weakly dispersive(WNWD)区域,相对于二维非线性浅水波方程,只是在动量方程中加入时间-空间的三阶导数项作为频散项,其频散性精确到Airy波精确解的Padé[0, 2]阶近似,属于二阶方程。与浅水波方程一样,仍然仅适合于浅水区域(水深小于1/5波长)。Boussinesq方程最早应用于求得二维孤立波的分析解,其考虑了水深变化,并将维度扩展到二维,成为经典的Boussinesq方程[36]。因为在经典的Boussinesq方程中,频散项是以水深平均速度的形式表示,这使得方程仅适用于波长大于5个水深的情况,为适应更多水波问题,前人改进了频散项[37]或将方程中的速度场用任意水深表示[38],使得对应的Boussinesq方程仅要求波长大于2个水深,这样大大扩展了Boussinesq方程的应用范围,改进之后的方程称为扩展型Boussinesq方程。
大部分Boussinesq方程在经扩展之后非线性增强,可适用于更为复杂的近岸水波波动情况,不再属于WNWD区域,而弱非线性弱频散性的Boussinesq方程更多是替代无频散性的非线性浅水波方程,以提高问题求解的精确度,反映更多的波浪运动的各种变形,如折射、绕射等。如Lynette和Liu[23]利用弱非线性Boussinesq方程模拟海底滑坡诱发的海啸,并讨论频散性在近岸水波模拟中的重要性。
2.3 经典的Hamilton正则方程除Boussinesq方程之外,在辛空间的Hamilton体系下建立的Hamilton正则方程, 同样可以为浅水波方程补充频散特性。与Euler空间下的Boussinesq方程不同的是,Hamilton描述没有对多个Laplace方程中的参数进行摄动展开,仅仅对速度势函数进行一次小参数展开,这样保持系统的对称性与守恒性,并且正则的方程意味着在数值求解时能保持长时间稳定。
利用Hamilton正则方程模拟近岸水波问题的开创性工作来自Zakharov[39],他提出正则共轭变量对(ζ, φ)的一对Hamilton正则方程表达式
| $ \frac{{\partial \zeta \left( {x,t} \right)}}{{\partial t}} = \frac{{{\rm{ \mathsf{ δ} }}E}}{{{\rm{ \mathsf{ δ} }}\varphi \left( {x,t} \right)}},\frac{{\partial \varphi \left( {x,t} \right)}}{{\partial t}} = - \frac{{{\rm{ \mathsf{ δ} }}E}}{{{\rm{ \mathsf{ δ} }}\zeta \left( {x,t} \right)}}. $ | (21) |
式中:δ表示泛函导数,E(x, ϕ, ζ)为流体的总能量(势能与动能之和),φ(x, t)为自由表面速度势。
与满足Laplace方程的流体速度势ϕ不同,Hamilton正则方程中考虑的速度势为自由表面速度势,这就说明Hamilton方程考虑的主体为自由面的水波特性,即不可作为内部流场的控制方程,所以将Hamilton正则方程引用在近岸弱非线性问题中时,经常用来分析表面波问题,如明渠波的自由表面波运动[40]。
以Zakharov的Hamilton正则方程的形式为基础,前人从非线性强耦合水波方程导出约化Hamilton正则方程[41-42],简化了结构,这种方法得到广泛应用[43-47]。由于该方法仍然基于波陡为小量的近似假设,所以仍然仅适合于弱非线性水波的情况。
3 近岸强非线性模型及适用现象强非线性水波问题主要有湍流模拟[48-49]、波群演变[50-51]、波浪越浪[52-57]、波流相互作用[58-59],常用构建模型的方法是Hilbert-Huang transform (HHT)方法、volume of fluid (VOF)方法、低级别的green-Naghdi理论、扩展后的Boussinesq方程。
3.1 Hilbert-Huang transform (HHT)方法在研究近岸有关水波、水流和外界相互作用的情况(如研究风力)时,风力对近岸波流的影响,一般都为强非线性,且常常具有强频散性、强瞬变性,而常用的傅里叶分析不能表达这些特性。为了能分析这类强非线性的近岸水波场景,可利用Huang等[60]发明的HHT方法进行水波观测数据的分析。
HHT方法属于图 2的strongly nonlinear and strongly dispersive (SNSD)区域。其基本思想是将任何时间数据整理成固有模态函数(intrinsic mode function),然后利用这些模态函数求其Hilbert变换,模态函数及其对应的Hilbert变换可以给出这个模态的波幅和波频。这样就得到随着时间变化的非线性波的内在性质,可综合分析其中体现的非线性、波散性和频散性。黄大吉等[61]进一步发展基于HHT方法的信号镜像闭合延拓和包络极值延拓两种方法,避免了Hilbert变换时出现的端点问题。
在实际应用方面,Huang等[48]利用他们自己的模型率先将HHT方法应用到强非线性、非稳态的Stokes波中,并探讨该方法在湍流问题中的应用。此外还可用HHT方法研究近岸波群的跨岸演变[50-51],分析热带海岸的高频、强非线性的水流波数据与温度数据之间的相互关系[62],研究湍流能量变化过程[49],模拟近岸地区空气中的大涡与海洋中强非线性波相互作用过程[63]等。
3.2 Volume of fluid (VOF)方法在处理近岸的两相流体问题时,对气液分界的自由表面做运动学追踪,一般采用VOF方法[64]。其思想与处理上岸问题中的干湿边界时相似,VOF引入比值标量函数Fc确定流场的自由面,Fc为网格内部的水流体积与网格体积之比,水体区域的Fc一般设置为1,气体区域的Fc设置为0,在自由面上Fc介于0到1之间。一般设近岸水体是不可压缩,则VOF函数满足方程
| $ \frac{{\partial {F_{\rm{c}}}}}{{\partial t}} + \mathit{\boldsymbol{v}} \cdot \nabla {F_{\rm{c}}} = 0. $ | (22) |
式中v是速度矢量。
以上则是自由表面追踪的VOF方程,利用该方程结合雷诺时均的Navier-Stokes方程即可对自由面进行追踪。追踪的内容包括下一时刻的VOF函数值,以及由VOF函数的分布得到的对自由面形状和位置的重构。重构方法多种多样,如几何重构法、施主-受主重构法等。
利用VOF方法建立波浪模型时,直接求解N-S方程,所以可以处理自由表面上的强非线性现象,如波浪翻滚、强烈破碎等。Shen等[65]基于VOF方法模拟强非线性波浪淹没沙坝的情况,还有研究利用VOF方法模拟近岸海堤上的爬坡、越浪问题[52-54, 56-57]。
3.3 低级别的Green-Naghdi理论Green-Naghdi理论是由于Demirbilek和Webster[66]推导的层析波浪理论控制方程,其假定流体不可压缩,并忽略其黏性。推导时,与浅水类方程不同,它不使用摄动展开,也不像Hamilton正则方程那样引入小参数,只是利用流层速度假设。以三维情况为例,流体层速度假设为
| $ \left\{ \begin{array}{l} u\left( {x,y,z,t} \right) = \sum\limits_{n = 0}^K {{u_n}\left( {x,y,z,t} \right){\lambda _n}\left( z \right)} \\ v\left( {x,y,z,t} \right) = \sum\limits_{n = 0}^K {{v_n}\left( {x,y,z,t} \right){\lambda _n}\left( z \right)} \\ w\left( {x,y,z,t} \right) = \sum\limits_{n = 0}^K {{w_n}\left( {x,y,z,t} \right){\lambda _n}\left( z \right)} \end{array} \right., $ | (23) |
式中:un, vn和wn是未知速度系数;K为整数,表示在Green-Naghdi理论的级别;λn(z)为形状函数,在近岸区域(属于浅水至有限水深领域),形状函数可取为
| $ {\lambda _n}\left( z \right) = {z^n},n = 1,2, \cdots ,K. $ | (24) |
具体的Green-Naghdi理论方程可参考文献[66]。
在实际应用方面,Kim等[67]利用无旋的G-N模型分析在倾斜沙滩上的波列的浅水作用。Bonneton等[68]总结G-N应用于非线性水波变形、破碎、上岸过程的研究。Chazel等[69]利用G-N理论制造一个强非线性强频散性波(SNSD wave)的传播,使该波传播过一个水底堤坝,最后分析所用数值方法的有效性以及系统的频散特性。赵彬彬等[59]利用第1至第3级别的Green-Naghdi理论研究周期性强非线性水波与剪切流的相互作用。段文洋等[70]分别对比第1至第7级别的Green-Naghdi理论与Boussinesq模型,用这两类模型模拟三维非线性波在圆形浅滩上的变形。
3.4 扩展后的Boussinesq方程在20世纪90年代以后,很多学者通过改进经典的Boussinesq方程,使得Boussinesq类模型能够扩大水深适用范围、模拟强非线性水波运动现象,使其能够应用与近岸更多的水波问题。
Wei等[71]最早改进经典的Boussinesq方程中的非线性性能,沿用Nwogu[38]的推导方法,但摒弃弱非线性的浅水假设,保留与色散项同阶的非线性项的所有阶项,由此产生完全非线性Boussinesq方程。尽管这样在一定程度上提高了方程非线性性能,但在深水情况下,方程的非线性精度却不如线性特征,这时需要另一种形式推导Boussinesq方程。Agnon等[72]基于Laplace方程,通过Padé近似和算子运算技术,得到静水面水平速度与垂直速度之间的关系,以自由面速度和自由面为特征变量,以此设置自由面的边界条件,最终通过速度势级数展开建立自由面速度变量和静水面速度变量之间的关系,得到Boussinesq类方程的新形式,后人称之为Agnon型Boussinesq方程。之后多人对Agnon型Boussinesq方程进行改进及应用工作[73-78],其中较为典型的工作来自Wang等[79],他们基于Agnon型Boussinesq的思路,将任意层速度替换原本的静水面水平速度,以任意层速度和垂向速度为特征速度,推导含背景水流影响的具有强非线性和强频散性的Agnon型Boussinesq方程。在无流的情况下,该方程的一维形式可表达为
| $ {\eta _t} - \tilde w + \tilde w{\eta _x} = 0, $ | (25) |
| $ \begin{array}{*{20}{c}} {{{\tilde q}_t} + g{\eta _x} + \tilde q{{\tilde q}_x} - {{\tilde w}^2}{\eta _x}{\eta _{xx}} - }\\ {\tilde w{{\tilde w}_x}\left( {1 + \eta _x^2} \right) = 0,} \end{array} $ | (26) |
| $ \begin{array}{*{20}{c}} {\left[ {\hat w - \frac{4}{9}{\gamma ^2}{{\hat w}_{xx}} + \frac{1}{{63}}{\gamma ^4}{{\hat w}_{xxxx}}} \right] + }\\ {\left[ {\gamma {{\hat u}_x} - \frac{4}{9}{\gamma ^3}{u_{xxx}} + \frac{1}{{945}}{\gamma ^5}{{\hat u}_{xxxxx}}} \right] + }\\ {\left[ {\gamma {{\hat u}_x} - \frac{4}{9}{\gamma ^3}{u_{xxx}} + \frac{1}{{945}}{\gamma ^5}{{\hat u}_{xxxxx}}} \right] + }\\ {{h_x}\left[ {\hat u - \left( {\frac{1}{3} - {b_1}} \right){\gamma ^2}{{\hat u}_{xx}} + \left( { - \frac{2}{{63}} - \frac{1}{6}{b_1} + {b_3}} \right){\gamma ^4}{{\hat u}_{xxxx}}} \right] - }\\ {{h_x}\left[ {\left( {1 - {b_1}} \right)\gamma {{\hat w}_x} - \left( { - \frac{1}{2}{b_1} + {b_3}} \right){\gamma ^3}{w_{xxx}}} \right] = 0,} \end{array} $ | (27) |
| $ \tilde q = \tilde u + \tilde w{\eta _x}, $ | (28) |
| $ \begin{array}{*{20}{c}} {\tilde u = \hat u - \frac{1}{2}\left( {\eta - \hat z} \right){{\hat u}_{xx}} + \frac{1}{{24}}\left( {\eta - \hat z} \right){{\hat u}_{xxxx}} + }\\ {\left( {\eta - \hat z} \right){{\hat w}_x} - \frac{1}{6}\left( {\eta - \hat z} \right){{\hat w}_{xxx}} + \frac{1}{{120}}\left( {\eta - \hat z} \right){{\hat w}_{xxxxx}},} \end{array} $ | (29) |
| $ \begin{array}{*{20}{c}} {\tilde w = \hat w - \frac{1}{2}\left( {\eta - \hat z} \right){{\hat w}_{xx}} + \frac{1}{{24}}\left( {\eta - \hat z} \right){{\hat w}_{xxxx}} - }\\ {\left( {\eta - \hat z} \right){{\hat u}_x} + \frac{1}{6}\left( {\eta - \hat z} \right){{\hat u}_{xxx}} + \frac{1}{{120}}\left( {\eta - \hat z} \right){{\hat u}_{xxxxx}}.} \end{array} $ | (30) |
式中:
在处理近岸波流相互作用问题时,弱非线性、弱色散性(WNWD)的Boussinesq方程可以适应于弱水流(流速的量级低于波浪的相速度的量级)的情况[80],但是近岸水域的水流流速一般比波浪的速度大,而比波浪的相速度小,但如果研究如港湾退潮、河口涌浪等问题时,通常水流流速比波浪的相速度要大,这样会造成波流之间的非线性作用增强,且逆流到达一定程度(如水流速度大于等于波浪能量传播速度)时波浪传播会受到阻碍,而被阻碍的波浪通常非线性和色散性都非常强。这样一来弱非线性弱色散性的Boussinesq方程就不适用了。Chen等[81]沿袭Yoon和Liu[80]的水流、波浪假设,推导适合强水流的强非线性、强频散性(SNSD)的Boussinesq方程。
4 近岸完全非线性模型及适用现象在处理近岸水波在海洋结构物(或障碍物)周围的实际工程问题(如非线性水波绕射问题[82-84]、辐射问题[84-85]、滑坡涌浪模拟[86]、水抨击问题[83, 87-89]、边带不稳定性[90]、马蹄波传播[91]等)时,常常需要利用到完全非线性模型。Longuet-Higgins等[92-93]最早提出完全非线性理论,他们应用边界元方法求解欧拉坐标下的流体方程,而采用拉格朗日坐标跟踪水质点,这也是后人所称的“混合欧拉-拉格朗日”(MEL)方法。完全非线性的数学物理含义为保留非线性指数的全部阶次,并为忽略任何非线性因素,浅水波方程和Boussinesq方程等时域模型都可以发展为完全非线性形式,高级别的Green-Naghdi理论也为完全非线性。完全非线性理论要求自由表面边界条件和物面边界条件分别在瞬时自由表面和瞬时物面上满足,在数值计算中要求保存每一时刻的自由水面和物面的位置,每一时刻都重新剖分网格并建立和求解代数方程。
前文提到Wei等[71]延续经典Boussinesq方程的推导,未做其他假设,并保留所有非线性阶次,最早推导了完全非线性Boussinesq方程。Gobbi和Kirby[94]在Wei等的理论基础上,进一步用两个水层的加权平均势函数和波面推导出改进的完全非线性Boussinesq方程。Madsen和Schäffer[95-96]采用Agnon型的Boussinesq方程,并将其改进为缓坡修正的完全非线性Boussinesq水波模型,并且研究近岸环流系统、边带不稳定性问题[90]、马蹄波(crescent waves)的传播[91]。赵曦等[97]将该模型应用于海啸生成与近岸传播。邹志利[98]基于势波理论,针对海底坡度较大的复杂地形,建立适用于近岸浅水区域的完全非线性Boussinesq方程。同年,Grilli[99]也从势流模型出发,通过求解完全非线性、完全频散性的势流方程,研究海底塌陷引发的海啸模型。邹志利[100]又从另一个角度出发,采用摄动法,建立可用于波流相互情况下的完全非线性Boussinesq方程。马小舟[101]从欧拉方程出发,建立适用于低频波浪的完全非线性Boussinesq方程。房克照[102]基于Madsen和Schäffer[96]的工作,利用完全非线性Boussinesq方程模拟浅水波和深水波在椭圆形、圆形浅滩上的波浪传播。
常用的近岸完全非线性模型是非线性、频散性都高达4阶的Boussiensq方程(BouN4D4)[11]。因为Boussinesq方程不能模拟波浪破碎,所以研究近岸完全非线性情况下的破碎间断问题时,常用完全非线性浅水波方程[89, 103]。
5 总结在国内外大量文献的基础上,对近岸区域波浪非线性传播的模型进行综述,从中可以了解到近岸的非线性水波问题相当丰富,非线性模型也多种多样,可以得到以下结论:
1) 在弱非线性水波问题中:在不考虑频散作用时,为了更高的求解效率,非线性浅水波方程最为合适,并且在进行数值方法改进(如进阶为更高阶的求解格式)、假设条件改进(如改为非静水压)时,浅水波方程更为直观简易;在考虑弱频散作用时,因为Hamilton正则方程自身的局限性,不可模拟内部流场,所以在研究如考虑频散效应的海啸波近岸传播问题时,应选用Boussinesq方程,研究近岸表面波问题时,则选用Hamilton正则方程可以有更好的数值稳定性。
2) 在强非线性问题中:若问题具有多因素的复杂性,如需要考虑温度、压力等多种条件,则可以选取HHT方法,因为该方法中的波频和波幅综合体现非线性波的内在性质;若需要研究干湿迅速交替变化的问题时,最适合选用自由表面追踪的VOF方法;如果问题中水体分层且需要考虑频散作用,则可选用低级别的Green-Naghdi理论;适用性最广的方程是扩展后的Boussinesq方程,它可以用来研究大部分近岸强非线性强频散性的水波问题。
3) 在完全非线性问题中:单一研究完全非线性时,完全非线性浅水波方程可以满足需求;在需要考虑频散性时,则常用完全非线性Boussinesq方程随着人们对近岸研究的深入,近岸水波模型向越来越强的非线性发展,由此可以研究更多自然界中可以观测到的强非线性水波问题,也能因此研究水波内在的特性。因为计算机性能的提高和数值计算的发展,各种数值求解技术得以更新和进步,近几年水波模型渐渐摆脱二维假设的限制而逐渐向三维发展,使得模拟更加贴近实际情况。另一个热门发展方向是向非静压条件发展,更多的学者建立非静压的非线性水波模型来研究近岸水波问题,这使得波浪的非线性作用有了新的内容。
在近岸非线性的数值模拟研究,控制方程不仅考虑波浪自身的非线性特性,也内含波流相互作用的非线性效应,同时不同的非线性项有助于对近岸水波问题理解,这有助于人们能够更好地利用近岸海洋资源,防治近岸海浪、海啸、风暴潮灾害。
| [1] |
陈雪堂.我国海洋环境污染问题研究[D].哈尔滨: 东北林业大学, 2004.
|
| [2] |
Satake K. Linear and nonlinear computations of the 1992 Nicaragua earthquake tsunami[J]. Pure & Applied Geophysics, 1995, 144(3/4): 455-470. |
| [3] |
李智广, 谢顺平, 都金康, 等. 海南岛及北部湾海域海啸数值模拟与影响分析[J]. 地球信息科学学报, 2015, 17(8): 937-944. |
| [4] |
任智源.南海海啸数值模拟研究[D].上海: 上海交通大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10248-1016787653.htm
|
| [5] |
王培涛, 于福江, 赵联大, 等. 2011年3月11日日本地震海啸越洋传播及对中国影响的数值分析[J]. 地球物理学报, 2012, 55(9): 3088-3096. |
| [6] |
张弛.渤海海域天文潮预报及海啸、寒潮数值模拟[D].天津: 天津大学, 2007. http://cdmd.cnki.com.cn/article/cdmd-10056-2008186176.htm
|
| [7] |
王培涛, 于福江, 范婷婷, 等. 海啸波传播的线性和非线性特征及近海陆架效应影响的数值研究[J]. 海洋学报, 2014, 26(5): 18-29. DOI:10.3969/j.issn.0253-4193.2014.05.003 |
| [8] |
Liu Y, Shi Y, Yuen D A, et al. Comparison of linear and nonlinear shallow wave water equations applied to tsunami waves over the China Sea[J]. Acta Geotechnica, 2009, 4(2): 129-137. DOI:10.1007/s11440-008-0073-0 |
| [9] |
赵永良, 张延廷. 浅海风暴潮和天文潮相作用中非线性效应的数值诊断分析[J]. 海洋学报, 1994, 16(1): 12-22. DOI:10.3321/j.issn:0253-4193.1994.01.008 |
| [10] |
余锡平. 近岸水波的解析理论[M]. 北京: 科学出版社, 2012.
|
| [11] |
李洪义.近岸水域波流相互作用的Boussinesq方程模拟[D].大连: 大连理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015571785.htm
|
| [12] |
Wu Y T, Yeh C L, Hsiao S C. Three-dimensional numerical simulation on the interaction of solitary waves and porous breakwaters[J]. Coastal Engineering, 2014, 85(1): 12-29. |
| [13] |
Zweifel A, Hager W H, Minor H E. Plane impulse waves in reservoirs[J]. Journal of Waterway Port Coastal & Ocean Engineering, 2006, 132(5): 358-368. |
| [14] |
Méhauté B L. An introduction to hydrodynamics and water waves[M]. Berlin: Springer-Verlag, 1976.
|
| [15] |
Sander J, Hutter K. On the development of the theory of the solitary wave:a historical essay[J]. Acta Mechanica, 1991, 86(1/4): 111-152. |
| [16] |
Watanabe A, Sato S. A sheet-flow transport rate formula for asymmetric, forward-learning waves and currents[C]//29th International Conference on Coastal Engineering, Lisbon ASCE, 2004: 1703-1714.
|
| [17] |
Elfrink B, Hanes D M, Ruessink B G. Parameterization and simulation of near bed orbital velocities under irregular waves in shallow water[J]. Coastal Engineering, 2006, 53(11): 915-927. DOI:10.1016/j.coastaleng.2006.06.002 |
| [18] |
Stoker J J. Water waves:the mathematical theory with applications[M]. New York: Interscience Publishers, Inc, 1957.
|
| [19] |
Monnier J, Couderc F, Dartus D, et al. Inverse algorithms for 2D shallow water equations in presence of wet dry fronts. Application to flood plain dynamics[J]. Advances in Water Resources, 2016, 97(7): 11-24. |
| [20] |
Le T T, Dang H P, Tran V C. Numerical simulation of tidal flow in Danang Bay based on non-hydrostatic shallow water equations[J]. Pacific Journal of Mathematics for Industry, 2016, 8(1): 1. DOI:10.1186/s40736-015-0020-6 |
| [21] |
Titov V V, Synolakis C E. Modeling of breaking and nonbreaking long-wave evolution and runup using VTCS-2[J]. Journal of Waterway Port Coastal & Ocean Engineering, 1995, 121(6): 308-316. |
| [22] |
Goto C, Ogawa Y, Shuto N, et al. IUGG/IOC time project, numerical method of tsunami simulation with the leap-frog scheme[M]. Paris: Ioc Manuals & Guides, 1997.
|
| [23] |
Lynett P, Liu P L-F. A numerical study of submarine-landslide-generated waves and run-up[J]. Proceedings Mathematical Physical & Engineering Sciences, 2002, 458(2028): 2885-2910. |
| [24] |
Romano M, Liong S Y, Vu M T, et al. Artificial neural network for tsunami forecasting[J]. Journal of Asian Earth Sciences, 2009, 36(1): 29-37. |
| [25] |
Kumar T S, Mahendra R S, Nayak S, et al. Coastal vulnerability assessment for Orissa State, East Coast of India[J]. Journal of Coastal Research, 2010, 26(3): 523-534. |
| [26] |
李林燕.南海海啸非线性反问题预报模式研究[D].北京: 清华大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10003-1012036227.htm
|
| [27] |
Arcos M E M, Leveque R J. Validating velocities in the GeoClaw Tsunami model using observations near Hawaii from the 2011 Tohoku Tsunami[J]. Pure & Applied Geophysics, 2015, 172(3/4): 849-867. |
| [28] |
Grilli S T, O'Reilly C, Harris J C, et al. Modeling of SMF tsunami hazard along the upper US East Coast:detailed impact around Ocean City, MD[J]. Natural Hazards, 2015, 76(2): 705-746. DOI:10.1007/s11069-014-1522-8 |
| [29] |
Sozdinler C O, Yalciner A C, Zaytsev A. Investigation of Tsunami hydrodynamic parameters in Inundation Zones with different structural layouts[J]. Pure & Applied Geophysics, 2015, 172(3/4): 931-952. |
| [30] |
Aricò C, Re C L. A non-hydrostatic pressure distribution solver for the nonlinear shallow water equations over irregular topography[J]. Advances in Water Resources, 2016, 98: 47-69. DOI:10.1016/j.advwatres.2016.10.015 |
| [31] |
Dodd N, Thornton E B. Longshore current instabilities: growth to finite amplitude[C]//International Conference on Coastal Engineering, 1993: 2655-2668.
|
| [32] |
Falqués A, Iranzo V. Numerical simulation of vorticity waves in the nearshore[J]. Journal of Geophysical Research Oceans, 1994, 99(C1): 825-841. DOI:10.1029/93JC02214 |
| [33] |
Feddersen F. Weakly nonlinear shear waves[J]. Journal of Fluid Mechanics, 1998, 372: 71-91. DOI:10.1017/S0022112098002158 |
| [34] |
沈良朵.缓坡沿岸流不稳定性特征研究[D].大连: 大连理工大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10141-1016033616.htm
|
| [35] |
Boussinesq J V. Theórie des ondes et des remous qui se propaent le long d'un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond[J]. Journal de Mathématiques Pures et Appliquées, 1872, 2(17): 55-108. |
| [36] |
Dh P. Long waves on a beach[J]. Journal of Fluid Mechanics, 1967, 27(4): 815-827. DOI:10.1017/S0022112067002605 |
| [37] |
Madsen P A, Sørensen O R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry[J]. Coastal Engineering, 1991, 15(4): 371-388. DOI:10.1016/0378-3839(91)90017-B |
| [38] |
Nwogu O. Alternative form of Boussinesq equations for nearshore wave propagation[J]. Journal of Waterway Port Coastal & Ocean Engineering, 1993, 119(6): 618-638. |
| [39] |
Zakharov V E. Stability of periodic waves of finite amplitude on the surface of a deep fluid[J]. Journal of Applied Mechanics & Technical Physics, 1968, 9(2): 190-194. |
| [40] |
Benjamin T B, C S J. Gravity-capillary waves with edge constraints[J]. Journal of Fluid Mechanics, 1979, 92(2): 241-267. |
| [41] |
Krasitskii V P. Canonical transformation in a theory of weakly nonlinear waves with a nondecay dispersion law[J]. Soviet Physics JETP, 1990, 71(5): 921-927. |
| [42] |
Krasitskii V P. On reduced equations in the Hamiltonian theory of weakly nonlinear surface waves[J]. Journal of Fluid Mechanics, 1994, 272: 1-20. DOI:10.1017/S0022112094004350 |
| [43] |
Sardanashvily G, Zakharov O. On application of the Hamilton formalism in fibred manifolds to field theory[J]. Differential Geometry & its Applications, 1993, 3: 245-263. |
| [44] |
Zakharov V E. Weakly nonlinear waves on the surface of an ideal finite depth fluid[J]. Am Math Soc Transl, 1998, 182(2): 167-197. |
| [45] |
Polnikov V G, Lavrenov I V. Calculation of the nonlinear energy transfer through the wave spectrum at the sea surface covered with broken ice[J]. Oceanology, 1999, 47(3): 334-343. |
| [46] |
Zaslavskii M M, Krasitskii V P. On the conversion of wave-gauge pressure data to the spectrum of surface waves[J]. Oceanology, 2001, 41(2): 184-188. |
| [47] |
Zaslavskii M M, Krasitskii V P. Stationary spectra of surface gravity waves in a finite-depth sea[J]. Izvestiya Atmospheric & Oceanic Physics, 2001, 37(1): 105-112. |
| [48] |
Huang N E, Shen Z, Long S R. A new view of nonlinear water waves:the Hilbert spectrum[J]. Ann Rev Fluid Mech, 1999, 31(1): 417-457. |
| [49] |
Huang Y, Biferale L, Calzavarini E, et al. Lagrangian single-particle turbulent statistics through the Hilbert-Huang transform[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2013, 87(4): 041003. |
| [50] |
Veltcheva A D. Wave and group transformation by a Hilbert spectrum[J]. Coastal Engineering Journal, 2002, 44(4): 283-300. DOI:10.1142/S057856340200055X |
| [51] |
Veltcheva A D. An application of HHT method to nearshore sea waves[M]//The Hilbert-Huang Transform in Engineering, Taylor & Francis: CRC Press, 2005: 97-119.
|
| [52] |
Guignard S, Marcer R, Rey V, et al. Solitary wave breaking on sloping beaches:2-D two phase flow numerical simulation by SL-VOF method[J]. European Journal of Mechanics-B/Fluids, 2001, 20(1): 57-74. DOI:10.1016/S0997-7546(00)01104-3 |
| [53] |
张九山, 吴卫, 王本龙, 等. 带异形块体海堤越浪的数值模拟[J]. 水动力学研究与进展, 2006, 21(5): 572-578. DOI:10.3969/j.issn.1000-4874.2006.05.003 |
| [54] |
Peng Z, Zou Q P. Spatial distribution of wave overtopping water behind coastal structures[J]. Coastal Engineering, 2011, 58(6): 489-498. DOI:10.1016/j.coastaleng.2011.01.010 |
| [55] |
Park H, Cox D T, Lynett P J, et al. Tsunami inundation modeling in constructed environments:a physical and numerical comparison of free-surface elevation, velocity, and momentum flux[J]. Coastal Engineering, 2013, 79(13): 9-21. |
| [56] |
杨锦凌, 孙大鹏, 吴浩, 等. 斜坡堤波浪爬高和越浪数值模拟[J]. 海洋工程, 2013, 31(2): 45-52. |
| [57] |
Cao H J, Wan D C. RANS-VOF solver for solitary wave run-up on a circular cylinder[J]. China Ocean Engineering, 2015, 29(2): 183-196. DOI:10.1007/s13344-015-0014-2 |
| [58] |
刘曾.稳态共振波及非线性波流相互作用研究[D].上海: 上海交通大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10248-1016787507.htm
|
| [59] |
赵彬彬, 杨婉秋, 王战, 等.非线性水波在线性剪切流中的时域模拟[C]//第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会, 2017: 252-258.
|
| [60] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995. |
| [61] |
黄大吉, 赵进平, 苏纪兰. 希尔伯特-黄变换的端点延拓[J]. 海洋学报, 2003, 25(1): 1-11. |
| [62] |
Ismail D K B, Lazure P, Puillat I. Application of Hilbert-Huang decomposition to temperature and currents data in the Réunion island[C]//Oceans 2016 MTS/IEEE, 2016: 1-9.
|
| [63] |
Hao X, Shen L. Simulation-based study of air-sea momentum fluxes nearshore[C]//APS Meeting, 2015.
|
| [64] |
Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. J Comput Phys, 1981, 39(1): 201-225. |
| [65] |
Shen Y M, Ng C O, Zheng Y H. Simulation of wave propagation over a submerged bar using the VOF method with a two-equation k-ε turbulence modeling[J]. Ocean Engineering, 2004, 31(1): 87-95. DOI:10.1016/S0029-8018(03)00111-2 |
| [66] |
Demirbilek Z, Webster W C. Application of the green-Naghdi theory of fluid sheets to shallow-water wave problems. Report 1. Model development[R]. US Army Wat Exp Sta, Coastal Eng Res Cntr Tech Rep, 1992, CERC-92-11: 45.
|
| [67] |
Kim J W, Bai K J, Ertekin R C, et al. A strongly-nonlinear model for water waves in water of variable depth:the irrotational green-Naghdi model[J]. Journal of Offshore Mechanics & Arctic Engineering, 2002, 125(1): 813-822. |
| [68] |
Bonneton P, Barthelemy E, Chazel F, et al. Recent advances in Serre-green Naghdi modelling for wave transformation, breaking and runup processes[J]. European Journal of Mechanics-B/Fluids, 2011, 30(6): 589-597. DOI:10.1016/j.euromechflu.2011.02.005 |
| [69] |
Chazel F, Lannes D, Marche F. Numerical simulation of strongly nonlinear and dispersive waves using a green-Naghdi model[J]. Journal of Scientific Computing, 2011, 48(1/3): 105-116. |
| [70] |
段文洋, 王战, 杨婉秋, 等.基于浅水层析波浪理论的波浪传播变形问题研究[C]//全国水动力学研讨会, 2017: 265-271.
|
| [71] |
Wei G, Kirby J T, Grilli S T, et al. A fully nonlinear Boussinesq model for surface waves. I. Highly nonlinear, unsteady waves[J]. Journal of Fluid Mechanics, 1995, 297: 71-92. |
| [72] |
Agnon Y, Madsen P A, Schäffer H A. A new approach to high-order Boussinesq models[J]. Journal of Fluid Mechanics, 1999, 399: 319-333. DOI:10.1017/S0022112099006394 |
| [73] |
Fuhrman D R, Bingham H B. Numerical solution of fully non-linear and highly dispersive Boussinesq equations in two horizontal dimensions[J]. International Journal for Numerical Methods in Fluids, 2004, 44(3): 231-255. DOI:10.1002/(ISSN)1097-0363 |
| [74] |
Bingham H B, Agnon Y. A Fourier-Boussinesq method for nonlinear water waves[J]. European Journal of Mechanics, 2005, 24(2): 255-274. DOI:10.1016/j.euromechflu.2004.06.006 |
| [75] |
张洪生, 冯文静, 商辉. 非线性波传播的新型数值模拟模型及其实验验证:引入变换速度变量[J]. 海洋学报, 2007, 29(4): 137-147. DOI:10.3321/j.issn:0253-4193.2007.04.016 |
| [76] |
张卫国, 陶涛. 强非线性广义Boussinesq方程孤波解的波形分析及求解[J]. 数学物理学报, 2008, 28(1): 86-95. |
| [77] |
Zhang H S, Wang W Y, Feng W J, et al. Tests and applications of a Boussinesq model with Ambient Current[J]. Journal of Hydrodynamics, 2010, 22(4): 526-536. DOI:10.1016/S1001-6058(09)60085-8 |
| [78] |
Zhang H S, Wang W Y, Feng W J, et al. A numerical model for nonlinear wave propagation on non-uniform current[J]. China Ocean Engineering, 2010, 24(1): 15-28. |
| [79] |
Wang Y L, Zhang H S, Miao G I, et al. A new approach to high-order Boussinesq-type equation with ambient currents[J]. China Ocean Engineering, 2005, 19(1): 49-60. |
| [80] |
Yoon S B, Liu P L F. Interactions of currents and weakly nonlinear water waves in shallow water[J]. Journal of Fluid Mechanics, 1989, 205(205): 397-419. |
| [81] |
Chen Q, Madsen P A, Schäffer H A, et al. Wave-current interaction based on an enhanced Boussinesq approach[J]. Coastal Engineering, 1998, 33(1): 11-39. |
| [82] |
Yang C, Ertekin R C. Numerical simulation of nonlinear wave diffraction by a vertical cylinder[J]. Journal of Offshore Mechanics & Arctic Engineering, 1991, 114(1): 34-44. |
| [83] |
W U G.X.. Hydrodynamic force on a rigid body during impact with liquid[J]. Journal of Fluids & Structures, 1998, 12(5): 549-559. |
| [84] |
Maiti S, Sen D. Time-domain wave diffraction of two-dimensional single and twin hulls[J]. Ocean Engineering, 2001, 28(6): 639-665. DOI:10.1016/S0029-8018(00)00025-1 |
| [85] |
Maiti S, Sen D. Nonlinear heave radiation forces on two-dimensional single and twin hulls[J]. Ocean Engineering, 2001, 28(8): 1031-1052. DOI:10.1016/S0029-8018(00)00043-3 |
| [86] |
黄波林.水库滑坡涌浪灾害水波动力学分析方法研究[D].武汉: 中国地质大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10491-1014340853.htm
|
| [87] |
Shi F, Kirby J T, Harris J C, et al. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation[J]. Ocean Modelling, 2012, 43/44(2): 36-51. |
| [88] |
Tissier M, Bonneton P, Marche F, et al. A new approach to handle wave breaking in fully non-linear Boussinesq models[J]. Coastal Engineering, 2012, 67(3): 54-66. |
| [89] |
房克照, 孙家文, 尹晶. 近岸波浪传播的非静压数值模型[J]. 水科学进展, 2015, 26(1): 114-122. |
| [90] |
Madsen P A, Bingham H B, Liu H. A new Boussinesq method for fully nonlinear waves from shallow to deep water[J]. Journal of Fluid Mechanics, 2002, 462: 1-30. DOI:10.1017/S0022112002008467 |
| [91] |
Fuhrman D R, Madsen P A, Bingham H B. A numerical study of crescent waves[J]. Journal of Fluid Mechanics, 2004, 513(513): 309-341. |
| [92] |
Longuet-Higgins M S, Cokelet E D. The deformation of steep surface waves on water. I. A numerical method of computation[J]. Proceedings of the Royal Society of London, 1976, 350(1660): 1-26. DOI:10.1098/rspa.1976.0092 |
| [93] |
Longuet-Higgins M S, Cokelet E D. The deformation of steep surface waves on water. Ⅱ. Growth of normal-mode instabilities[J]. Proceedings of the Royal Society A, 1978, 364(1716): 1-28. DOI:10.1098/rspa.1978.0185 |
| [94] |
Gobbi M C F, Kirby J T. Wave evolution over submerged sills:tests of a high-order Boussinesq model[J]. Coastal Engineering, 1999, 37(1): 57-96. |
| [95] |
Schäffer H A, Madsen P A. Further enhancements of Boussinesq-type equations[J]. Coastal Engineering, 1995, 26(1/2): 1-14. |
| [96] |
Madsen P A, Schäffer H A. Higher-order boussinesq-type equations for surface gravity waves:derivation and analysis[J]. Philosophical Transactions Mathematical Physical & Engineering Sciences, 1998, 356(1749): 3123-3184. |
| [97] |
ZhaoX, Liu H, Wang B L. Scenarios of local tsunamis in the China Seas by Boussinesq model[J]. China Ocean Engineering, 2014, 28(3): 303-316. DOI:10.1007/s13344-014-0025-4 |
| [98] |
邹志利. 适合复杂地形的高阶Boussinesq水波方程[J]. 海洋学报, 2001, 23(1): 109-119. DOI:10.3321/j.issn:0253-4193.2001.01.015 |
| [99] |
Grilli S E T. Modeling of tsunami generation by an underwater landslide in a 3D-NWT[C]//Proc of Offshore & Polar Eng Conf, 2001: 132-139.
|
| [100] |
邹志利. 含强水流高阶Boussinesq水波方程[J]. 海洋学报, 2000, 22(4): 41-50. DOI:10.3321/j.issn:0253-4193.2000.04.011 |
| [101] |
马小舟.近岸低频波浪的Boussinesq模拟[D].大连理工大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10141-2006146427.htm
|
| [102] |
房克照.四阶完全非线性Boussinesq水波方程及其简化模型[D].大连: 大连理工大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10141-2008069123.htm
|
| [103] |
Liang Q H. Flood simulation using a well-balanced shallow flow model[J]. Journal of Hydraulic Engineering, 2010, 136(9): 669-675. DOI:10.1061/(ASCE)HY.1943-7900.0000219 |
 2019, Vol. 36
2019, Vol. 36 


