2. 首都经济贸易大学信息学院, 北京 100070
2. School of Information, Capital University of Economics and Business, Beijing 100070, China
随着科学技术的进步和社会物质的富足,人类社会的分工合作趋于精细化和网络化。人们处于各种形形色色的复杂网络中,比如,与生活密切相关的社会网络[1]和铁路交通运输网[2],威胁人类健康的流行病疾病传播网络[3],以及威胁人类社会安定的恐怖组织网络[4]等等。现实网络中的节点地位存在明显的差异,关键节点相对于其他节点能更大程度地影响网络的结构和功能[5-6]。如何正确评价个人在社交网络中的地位、分析相互作用影响和关联关系,以及群体行为的效应等问题已经成为复杂网络研究中一项具有重要意义的课题。特别地,随着大数据时代的来临,关键节点的检测问题研究已经成为研究热点。其中复杂网络上节点积极效应研究涉及动力学、拓扑学、运筹学等多个学科的交叉应用,应用情景广泛,如社交网络中的谣言传播[7]、通讯网络中的病毒传播[8]、电力网络中的相继故障[9],以及经济网络中的危机扩散[10],等等。
在国内,众多学者们从不同的实际问题出发设计出各种各样的方法。孙睿和罗万伯[11]对网络舆情中节点重要性评估方法的研究现状进行综述,并从基于节点属性和网络拓扑结构两个方面,总结节点重要性的评价模型和方法。Hu等[12]将K壳分解法与社区结构相结合,提出一种改进指标,并在流行病传染模型领域上实证分析,验证该方法得到的关键传染源,相比K壳分解方法得到的传染源,具有更强的传播能力。赵之滢等[13]在复杂网络理论、动力系统理论与控制理论结合的基础上,开展复杂动态网络同步与控制理论的研究。利用网络中节点所关联的社团数目衡量节点的传播能力,提出一种基于网络社团结构的节点影响力度量方法,通过在Facebook社区、邮件通讯和博客平台等多个互联网领域数据集上实验评测,证实此方法能更有效地检测出互联网领域内信息传播能力较强的关键人物。
在国外,多个领域的学者对复杂网络关键节点挖掘的相关理论基础进行了探索性研究。Borgatti[14]率先提出KPP-POS (key player problem positive)的概念,即寻找一组关键节点用作信息扩散的种子可以最快速让信息在整个网络中扩散。Hussain[15]提出适应一般性系统的关于KPP问题的条件概率和熵度量的统计方法。为了更有效地找到最佳解决方案,Hamill等[16]提出基于对关键节点选择的有条件约束的线性规划问题。在线性规划问题基础上,McGuire和Deckro[17]进一步扩展到加权WKPP-Pos以便考虑节点的权重和边缘的关系权重。Yang[18]通过考虑网络的结构及其节点和边缘的属性,提出一个广义的关键节点问题GKPP (generalized key player problem)。
综上所述,利用数学规划的模型和思想研究网络关键节点检测问题属于学术前沿,相关理论和方法的研究也鲜有见闻。因此,本文基于网络的整体结构,考虑关键节点对网络积极效应的影响,采用数学规划的方法建立更加精确的模型并设计高效的求解算法,通过对这部分问题进行深入研究,完善关键节点检测理论和方法。
本文的主要贡献如下:
1) 基于对KPP-POS检测指标DR的优化,建立0-1整数线性规划的关键节点积极效应模型(0-1 integer linear programming key players problem positive effects model, IP-KPP-POS),用来解决社交网络关键节点检测积极效应的问题,并对该模型进行精确求解。
2) 设计局部搜索启发式算法对IP-KPP-POS模型进行求解,以适应不同规模网络的关键节点检测问题。并通过在特定随机图、多种类型随机网络以及真实标准网络数据集上的综合实验分析,验证本文所提出的模型在多个性能指标上的明显优势。
1 相关工作复杂网络关键节点的选择标准是多样的,有时需要初始免疫的节点在传染病扩散时能最大限度地保护全体人群,而有时需要破坏节点造成最广泛的连锁故障等等。因此,找到一个最佳量化节点在每种情况下的重要性的通用指标是不可能的[19]。Borgatti[14]最早给出社交网络关键节点消极效应和积极效应的正式定义,并提出DF指标和DR指标分别用来衡量网络的离散程度和网络的聚合程度。DF和DR指标具体表示如下:
| $ D_{\mathrm{F}} = 1-\frac{2 \sum\limits_{i>j} \frac{1}{d_{i j}}}{n(n-1)}, \quad D_{\mathrm{R}} = \frac{\sum\limits_{j} \frac{1}{d_{K j}}}{n-k} $ | (1) |
DF指标很好地刻画了网络的离散程度,但直接对DF指标进行优化存在计算上的不可行性。为解决当前所面临的问题,Arulselvan等[20]针对社交网络关键节点消极效应问题建立0-1整数线性规划模型并设计启发式算法进行求解,取得了较好的实验效果。然而,该模型只考虑连通分支内节点的个数,而忽视了连通分支内部的结构,不能有效优化连通分支的内部结构。为了更好地优化连通分支的内部结构,Jiang等[21]对DF指标进行近似,综合考虑剩余网络的一步连通性和两步连通性,开创性地建立0-1二次约束二次规划模型并设计算法进行求解,填补了将DF指标融入数学规划模型研究的空白。
然而到目前为止,关于如何将积极效应指标DR融入数学规划的模型中,采用系统的方法检测关键节点研究的更是接近空白。本文在现有研究的基础上,基于对KPP-POS检测指标DR的优化,针对社交网络关键节点检测积极效应问题,建立0-1整数线性规划的关键节点积极效应模型,并设计一种计算复杂度较低且精确度较高的局部搜索启发式算法对网络的关键节点进行识别。
本文所研究的社交网络关键节点检测积极效应问题(KPP-POS)具体是指:给定无向图G(V, E)和正整数K,从节点集合V中选择K个节点子集合,使其关联节点的总数最多,从而达到最大传播效应的目的。这个问题的本质是计算一组节点成员(KP集)与另一组节点成员(网络的其余部分)之间的连接(内聚)强度。函数指标DR就很好地描述了集合K的成员与网络的剩余部分(V-K)之间的内聚程度。
其中,dKj定义为从集合K到剩余部分节点j的最小距离,分子表示为从KP集合到所有剩余节点的最小距离的倒数之和,分母功能是标准化度量指标,即DR∈[0, 1]。DR可看作是KP集合节点达到其余所有节点的加权比例,并且到达其他节点的权值和它们最小距离成反比。当且仅当距离为1时,节点被赋予最大权值1。因此,当每个外部节点与KP集合的至少一个成员相邻(即KP集合是支配集合)时,DR取最大值1。当KP集合的任何成员都不与外部节点集的成员相邻,即KP集完全离散时,得到最小值0。
2 IP-KPP-POS模型建立公式(1)给出衡量网络聚合程度的指标DR,虽然DR考虑了距离加权,但是DR指标包含最短路径dKj的求解,直接把DR作为目标进行优化复杂度高,求解困难。另外,对于一步可达路径dij = 1, 1/dij = 1;对于两步可达路径dij = 2, 1/dij = 1/2;dij≥3, 1/dij相应减少为1/3,1/4, …, 0。在资源有限或成本约束条件下,可以假设两步和两步以上可达路径在实际中是不连通的,在此假设条件下,对DR的优化就简化为对一步可达路径节点对的连通性能最大化优化问题。
基于对KPP-POS的检测指标DR的优化, 建立考虑网络内部距离加权的深入优化的0-1整数线性规划的关键节点积极效应模型(0-1 Integer linear programming key players problem positive effects model, IP-KPP-POS),具体模型表示如下。
| $ {{S}_{\text{KPP}-\text{POS}}} = \left\{ n|{{y}_{n}} = 1 \right\}. $ | (2) |
| $ \max \sum\limits_{i}{\sum\limits_{j}{{{a}_{ij}}}}\cdot {{x}_{ij}}. $ | (3) |
| $ \text{s}\text{.t}\text{. }\sum\limits_{j = 1}^{N}{{{x}_{ij}}} = 1, \forall i\in V. $ | (4) |
| $ \sum\limits_{j = 1}^{N}{{{y}_{j}}} = K. $ | (5) |
| $ {{x}_{ij}}\le {{y}_{j}}, \forall i, j\in V. $ | (6) |
| $ {{x}_{ij}}\in \{0, 1\}, \forall i, j\in V. $ | (7) |
| $ a_{i j} \in\{0, 1\}, \forall i, j \in V. $ | (8) |
模型变量解释如表 1所示。
|
|
表 1 模型变量解释 Table 1 Explanations of model variables |
约束(4)迫使每个网络的其余部分节点最多只受一个关键节点影响;约束(5)在资源有限条件下限制网络关键节点的总数量;约束(6)允许只有当前位置为关键节点时,点i才能受点j影响。
为快速求解,本文采用MATLAB中内置的Integer Linear Programming算法包对IP-KPP-POS模型求解;已有文章证明,网络关键节点检测问题是NP-complete的[20]。因此,为适应大规模网络的求解,本文在第3节中设计启发式算法进行求解。
3 启发式算法设计 3.1 贪婪算法设计最近,已有学者提出针对社交网络关键节点检测积极效应问题求解的KPP-POS贪婪算法,并通过实验证实了该算法的有效性[14]。KPP-POS贪婪算法如表 2所示。
|
|
表 2 关键节点检测的贪婪算法 Table 2 Greedy algorithm for key players detection |
这个算法首先随机选择k个节点作为关键节点填充集合S,然后设置合适的初始目标值。随后对集合S中的每个节点u和每个不在集合S中的节点v进行交换,如果目标值得到改善,那就进行交换并更新目标值,反之取消交换,直到目标值不再得到优化时程序终止。
由于此贪婪算法选取起始关键节点集采用随机的方式,所以运行结果容易陷入局部最优解。为有效地解决该问题,通常使用数十个随机起始集重复实验,最终选取实验结果最好的目标值对应的关键节点集S,但同时也增加整个求解过程的运行时间,即减缓全局收敛速度。
3.2 贪婪结合局部搜索的启发式算法为了能够求解较大规模社交网络关键节点检测积极效应问题,本文在贪婪框架内结合局部搜索方法,设计了一个启发式算法。如表 3所示。
|
|
表 3 关键节点检测的启发式算法 Table 3 Heuristic algorithm for key players detection |
这个算法首先选择能够使得目标值最优的第一个节点,即所有节点中度最大的一个节点。然后在删除已选择的关键节点的剩余网络中,加入可以使目标值最优的下一个节点,通过局部搜索方法,每次从已选择作为关键节点的集合中取出一个节点,与剩余网络中的一个节点置换,如果可以增加目标值(目标值为max),那么进行置换;反之,取消置换。同理,按照该方法对集合中的其他节点做置换尝试,直至选择的关键节点个数达到预先设定的K值。
该启发式算法起始集选择使得目标值最优的节点,这种起始集的选择减少了得到局部最优解的可能并且加快了全局收敛速度。显而易见,该启发式算法的主要消耗在局部搜索增强操作上,复杂度为O(N)。
4 实验分析本章节将通过在特定随机图,多种类型随机网络和真实标准网络数据集上同KPP-POS贪婪算法综合实验对比分析,对提出的IP-KPP-POS模型、IP-KPP-POS启发式算法进行验证。其中,IP-KPP-POS模型、IP-KPP-POS启发式算法都是使用MATLAB语言编程开发的,所有的模型和算法均在配置为Windows操作系统的台式机电脑平台上运行。平台的具体配置为:主频2.6 GHz的骁龙CPU;32 G的内存。
4.1 特定E-R随机图如图 1所示,本文在节点规模为15,边规模为41,连接密度为30%的ER随机生成图上进行阐述。以DR指标作为网络积极效应的评测标准,根据前文对DR的定义,当DR值越大,说明选择的一组节点(KP集)的成员与另一个节点(网络的其余部分)的成员之间的连接或内聚越强,即更具有重要性;反之亦然。实验结果如表 4所示。

|
Download:
|
| 图 1 特定E-R随机图 Fig. 1 A specific E-R random graph | |
|
|
表 4 特定E-R随机图上的实验分析 Table 4 Experimental analysis on a specific E-R random graph |
表 4中,前两列分别表示实验中网络的节点数和边数,第3列表示关键节点的个数K值;Obj表示对应方法求解所得到的目标值,KP集表示求解得到的关键节点集,T表示方法求解时间,单位为ms;而DR表示衡量网络凝聚程度的优化效果指标。上标“*”表示针对同一网络优化效果更好的一方。
当K值分别取1、2和3,即网络中作为关键节点的节点数目分别为1、2和3时,3种方法的DR值都相同。这意味着在关键节点数目分别为1、2和3时,IP-KPP-POS模型和IP-KPP-POS启发式算法跟KPP-POS贪婪算法在网络积极效应优化效果一致,但IP-KPP-POS启发式算法的运行时间要明显优于IP-KPP-POS模型和KPP-POS贪婪算法。
4.2 多种类型随机网络为测试不同K值下,IP-KPP-POS模型和IP-KPP-POS启发式算法的性能,针对节点数为20、50、70、120,边数分别为56、383、683、1 538,连接密度为30%的随机网络图,同KPP-POS贪婪算法进行实验对比分析,实验结果如表 5所示。
|
|
表 5 多种类型随机网络上的实验分析 Table 5 Experimental analysis on various types of random networks |
表 5中,前两列分别表示实验中网络的节点数和边数,第3列表示关键节点的个数K值;Obj表示对应方法求解所得到的目标值,T表示方法求解时间,单位为ms;而DR表示衡量网络凝聚程度的优化效果指标。上标“*”表示针对同一网络优化效果更好的一方。例如,第1行至第3行表示对于一个节点数为20,边数为56的网络图,当K值分别为1、2、3时,IP-KPP-POS模型、IP-KPP-POS模型启发式算法和KPP-POS贪婪算法的优化效果对比分析。
从第9行可以看出,当N = 70,E = 683,K = 3时,IP-KPP-POS模型、IP-KPP-POS模型的启发式算法和KPP-POS贪婪算法的最优值为分别为57、55和55,网络的DR值分别为0.925 4、0.910 4和0.910 4,IP-KPP-POS模型的启发式算法优化效果和KPP-POS贪婪算法相同,但是IP-KPP-POS模型的启发式算法的求解时间远远优于KPP-POS贪婪算法和IP-KPP-POS模型的求解时间,而且IP-KPP-POS模型的优化效果明显优于IP-KPP-POS模型的启发式算法和KPP-POS贪婪算法。
从整体的对比实验结果来看,虽然IP-KPP-POS模型的求解时间要比KPP-POS贪婪算法的求解时间长,但是IP-KPP-POS模型的求解精度要比KPP-POS贪婪算法更高;同时在同样的优化效果下,IP-KPP-POS模型的启发式算法的求解时间远远优于KPP-POS贪婪算法和对应的IP-KPP-POS模型的求解时间。此外,IP-KPP-POS模型的启发式算法和IP-KPP-POS模型求解的结果大部分一致,这也证实了启发式算法的正确性。
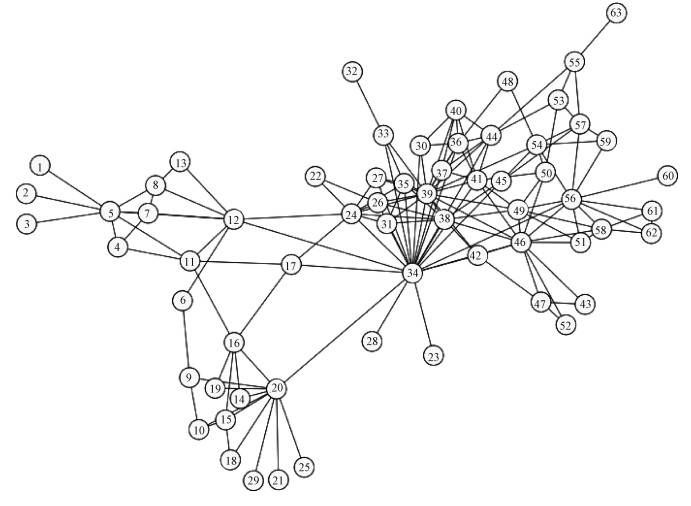
4.3 真实恐怖网络数据集为验证IP-KPP-POS模型在真实网络上的性能,本节在如图 2所示的真实恐怖网络数据集上进行实验分析,实验结果如表 6所示。
|
Download:
|
| 图 2 “9.11”恐怖网络数据集 Fig. 2 "9.11" terrorist network dataset | |
|
|
表 6 真实恐怖网络数据集上的实验比较 Table 6 Comparison on a real terror network dataset |
Krebs的911劫持者数据集:以下数据集是由Krebs使用关于9/11恐怖分子的开源文献编制的[22]。该数据集包含与911事件相关的恐怖主义袭击事件人员之间的所有联系。数据集包含63个节点和154条边。
当K值取3,也就是网络中作为关键节点的节点数目为3时,Borgatti的Key Player Set模型[14]和McGuire的WKPP-Pos模型[17]选择的节点集都是5、34和46,DR值为0.788 9;而本文所建立的IP-KPP-POS模型选择的是节点集是20、34和56,DR值为0.811 1,优化效果明显好于0.788 9。通过比较可以看出,本文建立的IP-KPP-POS模型在真实恐怖网络数据集上网络积极效应优化效果相比其他方法明显占优。
4.4 Facebook数据集由于IP-KPP-POS模型的算法复杂度较高,求解算法又受到MATLAB的内置约束限制,目前在现有平台只能求解节点规模小于100的网络。为验证在大规模网络上的性能,本章节在开源评测数据集网络“Facebook数据集”[23]上对比IP-KPP-POS启发式算法和KPP-POS贪婪算法,该数据集包含347个节点和5 038条边。实验结果如表 7所示。
|
|
表 7 Facebook数据集上的实验比较 Table 7 Comparisons on the Facebook dataset |
从表 7可以看出,当网络规模增加到347时,IP-KPP-POS启发式算法的平均运行时间为2.3e2,而KPP-POS贪婪算法的平均运行时间为2.2e3,KPP-POS贪婪算法大约是IP-KPP-POS启发式算法平均运行时间的10倍。从DR的结果对比来看,IP-KPP-POS启发式算法所选择的关键节点集,优于KPP-POS贪婪算法所选择的关键节点集。
对于更大规模的网络,论文同样进行了实验分析。由于KPP-POS贪婪算法的复杂度远高于IP-KPP-POS启发式算法的复杂度。随着网络规模的增加,KPP-POS贪婪算法的计算运行时间大幅增加。当网络规模为958时,IP-KPP-POS启发式算法运行时间平均为1.7e5,而KPP-POS贪婪算法的运算时间平均为2.0e6。因此,在现有的计算资源有限的平台约束下,因缺少对照实验数据,很难进行更大规模网络数据集的验证评测。在未来研究中,可以增加计算资源,在更大规模的网络数据集上进行实验对照分析。
4.5 实验结果为了评测IP-KPP-POS模型以及IP-KPP-POS启发式算法的有效性和正确性,同KPP-POS贪婪算法在特定E-R随机图,多种类型随机网络以及真实标准网络数据集上进行对比实验。实验表明,本文所提出的模型方法在多个性能指标上具有明显优势。特别地,在小数据集上,IP-KPP-POS模型以及IP-KPP-POS启发式算法在网络积极效应优化方面同样出色;但随着数据规模的扩大,IP-KPP-POS模型检测到的关键节点在网络积极效应优化精确度上比IP-KPP-POS启发式算法和KPP-POS贪婪算法的精确度更高一些,但是IP-KPP-POS启发式算法的求解时间要明显优于IP-KPP-POS模型和KPP-POS贪婪算法的求解时间。
5 总结在本文中,我们提出一种新的方法IP-KPP-POS解决复杂网络关键节点检测积极效应问题。由于问题的NP难特性,又对该模型的求解算法深入研究。一方面,利用0-1整数线性规划方法对模型求解,满足小规模网络的快速精确求解;另一方面,设计贪婪局部搜索的启发式算法,满足大规模网络的节点检测。通过在E-R随机网络、多种类型随机图、真实恐怖网络、Facebook数据集等多种数据集上同KPP-POS贪婪算法进行对比实验,验证模型的正确性和有效性。实验结果表明,本文提出的IP-POS-CNP模型,在准确性能上明显高于传统的KPP-POS方法,并且所设计的对应的启发式算法在求解速度上具有显著优势,更加适合大规模网络关键节点的快速检测。本文的研究成果可为各领域的关键节点相关问题提供决策支持。在未来的研究中,本文将对有向有权图中关键节点的挖掘进一步探索研究。
| [1] |
Borgatti P, Mehra A, Brass J, et al. Network analysis in the social sciences[J]. science, 2009, 323(5916): 892-895. DOI:10.1126/science.1165821 |
| [2] |
王伟, 刘军, 蒋熙, 等. 中国铁路网的拓扑特性[J]. 北京交通大学学报, 2010, 34(3): 148-152. DOI:10.3969/j.issn.1673-0291.2010.03.029 |
| [3] |
Zhou T, Fu Z Q, Wang B H. Epidemic dynamics on complex networks[J]. Progress in Natural Science, 2005, 16(5): 452-457. |
| [4] |
Latora V, Marchiori M. How the science of complex networks can help developing strategies against terrorism[J]. Chaos, Solitons and Fractals, 2004, 20(1): 69-75. |
| [5] |
Albert R, Jeong H, Barabasi A L. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6794): 378-382. DOI:10.1038/35019019 |
| [6] |
Kurant M, Thiran P, Hagmann. Error and attack tolerance of layered complex networks[J]. Physical Review E, 2007, 76(2): 026103. DOI:10.1103/PhysRevE.76.026103 |
| [7] |
朱冠桦, 蒋国平, 夏玲玲. 社交网络上从众现象对谣言传播影响的研究[J]. 计算机科学, 2016, 43(2): 135-139. |
| [8] |
韩江漫. 基于动态复杂网络技术的病毒传播控制策略研究[J]. 计算机与数字工程, 2017, 45(10): 2004-2008. DOI:10.3969/j.issn.1672-9722.2017.10.024 |
| [9] |
曹照.基于相继故障的复杂脑网络研究[D].兰州: 兰州理工大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10731-1016906289.htm
|
| [10] |
薛红艳.金融危机通过资本市场对我国经济扩散研究[D].保定: 河北大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10075-1014039106.htm
|
| [11] |
孙睿, 罗万伯. 网络舆论中节点重要性评估方法综述[J]. 计算机应用研究, 2012, 29(10): 3606-3608. DOI:10.3969/j.issn.1001-3695.2012.10.002 |
| [12] |
Hu Q C, Gao Y, Ma P F, et al. A new approach to identify influential spreaders in complex networks[C]//Web-Age Information Management, Lecture Notes in Computer Science, New York: Springer, 2013, 62(14): 99-104.
|
| [13] |
赵之滢, 于海, 朱志良, 等. 基于网络社团结构的节点传播影响力分析[J]. 计算机学报, 2014(4): 753-766. |
| [14] |
Borgatti S P. Identifying sets of key players in a social network[J]. Computational & Mathematical Organization Theory, 2006, 12(1): 21-34. |
| [15] |
Hussain D M A. Investigation of key-player problem in terrorist networks using Bayes conditional probability[M]. Handbook of Social Network Technologies and Applications, 2010: 523-547.
|
| [16] |
Hamill J T, Deckro R F, Chrissis J W, et al. Analysis of layered social networks[J]. IO Sphere, 2008(1): 27-33. |
| [17] |
McGuire R M, Deckro R F. The weighted key player problem for social network analysis[J]. Military Operations Research, 2015, 20(2): 35-53. |
| [18] |
Yang J. Generalized key player problem[J]. Computational & Mathematical Organization Theory, 2015, 21(1): 24-47. |
| [19] |
Lü L, Chen D, Ren X L, et al. Vital nodes identification in complex networks[J]. Physics Reports, 2016, 650: 1-63. DOI:10.1016/j.physrep.2016.06.007 |
| [20] |
Arulselvan A, Commander C W, Elefteriadou L, et al. Detecting critical nodes in sparse graphs[J]. Computers and Operations Research, 2009, 36(7): 2193-2200. DOI:10.1016/j.cor.2008.08.016 |
| [21] |
Jiang C, Wang J Y, Yu H, et al. An optimal approach for critical node problem using semidefinite programming[J]. Physica A:Statistical Mechanics and its Application, 2017, 471: 315-324. DOI:10.1016/j.physa.2016.11.071 |
| [22] |
Krebs V E. Uncloaking terrorist networks[J/OL]. First Monday, 2002, 7(4)[2017-12-20]. http://firstmonday.org/ojs/index.php/fm/article/view/941/86.
|
| [23] |
Mcauley J, Leskovec J. Learning to discover social circles in ego networks[C]//International Conference on Neural Information Processing Systems. Curran Associates Inc, 2012: 539-547.
|
 2019, Vol. 36
2019, Vol. 36 


