2. 中国科学院大学, 北京 100049;
3. 芬兰地球空间研究所, 马萨拉 FI-02430
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Finnish Geospatial Research Institute, Masala FI-02430, Finland
长期以来,激光雷达作为获取目标三维坐标信息的利器,在地形测绘、森林资源调查、三维建模、海洋探测、深空探测、军事应用等领域都发挥了重要作用。但传统三维激光雷达应用更多地偏重于数据中所包含的目标空间信息,而忽略其中包含的目标辐射信息,使得激光雷达数据的应用存在很多局限性。近年来,随着全波形激光雷达、多光谱/高光谱激光雷达技术的不断发展,激光雷达回波强度数据的重要性逐渐受到广泛关注。激光雷达回波强度数据记录地物目标与发射激光光束作用后的后向散射回波信息,能够表征地物目标对激光信号的散射能力的强弱和目标辐射特性信息,有效弥补传统三维激光雷达数据在目标辐射特性获取方面的缺失。激光雷达回波强度数据在地物目标信息提取中的作用以及应用中存在的问题逐渐成为近年来激光雷达技术领域的研究热点。
Kaasalainen等[1]利用机载激光雷达对不同反射率的地物目标进行实验,发现在均匀亮度、垂直照射情况下激光雷达回波强度数据存在显著差异。Schmidt等[2]的研究发现,激光雷达强度信息可用于地面覆盖物的区域划分和地物分类。Yan等[3]的研究表明,激光雷达强度数据经过一些简单校正后,能够有效改善地物信息提取的适用性与精确性。谭凯等[4]针对入射角和传输距离对于激光雷达回波强度数据的影响,提出基于多项式的强度校正模型以减小同类目标回波强度的差异。Xu等[5]利用RIEGL VZ-400i回波强度数据,结合目标粗糙度对于后向散射的影响,针对入射角和传输距离的影响分别提出回波强度校正方法,有效提高反演目标反射率参数的精度。
越来越多的研究显示出激光雷达回波强度数据在目标探测与识别、信息提取与挖掘、定量化遥感参数反演等方面有着非常广阔的应用前景,激光雷达回波强度的重要性受到广泛关注。但是,目前针对激光雷达回波强度数据辐射机理与辐射特性的研究有待深入开展,激光雷达后向散射的目标反射特性定义以及回波强度辐射特征在定量遥感应用中的物理意义尚不明确,激光雷达回波强度信息的遥感定量应用还有很多问题需要解决。
本文从激光雷达辐射传输机理出发,首先构建具有明确物理意义的激光雷达回波强度数据辐射传输机理方程,基于该方程系统性地探讨和分析激光雷达回波强度数据的辐射特征和关键影响因素,并利用搭建的激光雷达实验平台对激光雷达辐射特性进行验证和讨论。本文采用理论分析和实验验证相结合的方式,系统性分析激光雷达回波强度数据的辐射特性和变化规律,研究结论可为开展激光雷达辐射定标、辐射校正, 以及各种定量化应用提供必要的理论依据和技术支持。
1 激光雷达辐射传输机理 1.1 激光雷达辐射传输方程激光雷达主动发射激光信号并传输到目标,经目标后向散射再传输回激光雷达[6],这一过程可用激光雷达传输方程[7]表示:
| $ {P_{\rm{s}}} = \frac{{{P_{\rm{i}}}D_{\rm{r}}^2}}{{4{\rm{ \mathsf{ π} }}{R^4}\beta _{\rm{t}}^2}}{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}\sigma , $ | (1) |
式中:Ps为激光雷达接收到的回波信号功率;Pi为激光雷达发射信号功率;Dr为激光雷达接收孔径;R为目标与激光雷达之间的距离;βt为激光发散角;ηsys为激光雷达系统参数;ηatm为信号在大气传输过程中的影响因子;σ为后向散射截面,与地物的反射特性相关。
基于电磁场理论,后向散射截面σ可定义为
| $ \sigma = \mathop {\lim }\limits_{R \to \infty } \frac{{4{\rm{ \mathsf{ π} }}{R^2}\left\langle {{\mathit{\boldsymbol{E}}_{\rm{s}}} \cdot \mathit{\boldsymbol{E}}_{\rm{s}}^*} \right\rangle }}{{{{\left| {{\mathit{\boldsymbol{E}}_{\rm{i}}}} \right|}^2}}}. $ | (2) |
式中,Ei、Es分别表示入射和散射的电磁场矢量。
激光雷达反射率ρ(Ωi, Ωs)又可定义为
| $ \rho \left( {{\mathit{\Omega }_{\rm{i}}},{\mathit{\Omega }_{\rm{s}}}} \right) = \frac{{{P_{\rm{s}}}\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}};{\mathit{\Omega }_{\rm{s}}}} \right)}}{{{P_{\rm{i}}}\left( {{\theta _{\rm{s}}},{\phi _{\rm{s}}};{\mathit{\Omega }_{\rm{s}}}} \right)}} = \frac{{{A_{\rm{r}}}{{\left| {{\mathit{\boldsymbol{E}}_{\rm{s}}}} \right|}^2}}}{{{A_{\rm{i}}}\cos {\theta _{\rm{i}}}{{\left| {{\mathit{\boldsymbol{E}}_{\rm{i}}}} \right|}^2}}}, $ | (3) |
式中:Ωi和Ωs分别表示激光雷达入射方向和后向散射方向上的立体角;θi为入射天顶角(以下简称入射角),ϕi为入射方位角;θs为后向散射天顶角(以下简称出射角),ϕs为后向散射方位角; Ar、Ai分别表示激光雷达接收孔径面积和投射到目标上的光斑面积。则后向散射截面σ与激光雷达反射率ρ(Ωi, Ωs)之间有如下关系
| $ \sigma = \frac{{4{\rm{ \mathsf{ π} }}}}{{{\mathit{\Omega }_{\rm{s}}}}}\rho \left( {{\mathit{\Omega }_{\rm{i}}},{\mathit{\Omega }_{\rm{s}}}} \right){A_{\rm{i}}}\cos {\theta _{\rm{i}}}, $ | (4) |
式中:Aicosθi为光斑有效面积,可以表示为
| $ {A_{\rm{i}}}\cos {\theta _{\rm{i}}} = \frac{{{\rm{ \mathsf{ π} }}{R^2}\beta _{\rm{t}}^2}}{4}. $ | (5) |
对于激光雷达,一般认为入射立体角Ωi与后向散射立体角Ωs都非常小,推导激光雷达反射率ρ(Ωi, Ωs)与二向性反射率分布函数(bidirectional reflectance distribution function,BRDF)f(θi, ϕi, θs, ϕs)之间有如下关系[8]
| $ \rho \left( {{\mathit{\Omega }_{\rm{i}}},{\mathit{\Omega }_{\rm{s}}}} \right) = < f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) > {\mathit{\Omega }_{\rm{s}}}\cos {\theta _{\rm{s}}}. $ | (6) |
式中:< f(θi, ϕi, θs, ϕs)>表示在Ωi与Ωs范围内的BRDF的统计均值。则后向散射截面σ与BRDF有如下关系
| $ \sigma = 4{\rm{ \mathsf{ π} }} < f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) > {A_{\rm{i}}}\cos {\theta _{\rm{i}}}\cos {\theta _{\rm{s}}}. $ | (7) |
将式(5)、式(7)代入到式(1),可得到目标回波强度与BRDF有如下关系
| $ {P_{\rm{s}}} = \frac{{{\rm{ \mathsf{ π} }}{P_{\rm{i}}}D_{\rm{r}}^2}}{{4{R^2}}}{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}} < f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) > \cos {\theta _{\rm{s}}}. $ | (8) |
该公式构建了具有明确物理意义的激光雷达回波强度数据辐射传输机理方程。可以看出,激光雷达发射信号功率Pi,激光发散角βt, 激光雷达接收孔径Dr, 系统参数ηsys和大气影响因子ηatm在激光雷达系统性能稳定和飞行试验条件不变的情况下可看作是不变的常数。影响激光雷达回波强度的主要外部因素有:目标反射特性、目标与激光雷达系统之间的传输距离R、入射角θi/出射角θs(对于激光雷达,发射方向与探测方向几乎一致,所以θi = θs)。此外,激光雷达回波强度Ps的记录表征方式以及发射与接收过程的噪声,也将影响回波强度数据。
1.2 激光雷达回波强度的数据记录方式不同的激光雷达系统,其记录回波强度信息的方式各不相同,如回波波形、回波峰值、回波宽度、回波波形积分值等,目前并没有统一的标准,因此难以和接收到的回波强度定量联系起来,真实反映目标物的辐射特征。本节将基于前面推导的激光雷达辐射传输方程,推导能关联目标辐射特性的记录方式下的回波强度数据的仿真表达式,并在后面的分析中,利用该仿真分析激光雷达回波强度数据的辐射特征。
在实际应用中,激光雷达系统连续不断地向目标发射被调制为高斯函数形式的时域脉冲信号。设Pi(t)为激光雷达发射信号,Ps(t)为接收的回波信号,式(1)的时间域表示形式[9]如下:
| $ {P_{\rm{s}}}(t) = \frac{{D_{\rm{r}}^2}}{{4{\rm{ \mathsf{ π} }}\beta _{\rm{t}}^2{R^4}}}{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}{P_{\rm{i}}}(t) * \sigma (t), $ | (9) |
| $ {P_{\rm{i}}}(t) = {\hat P_{\rm{i}}}{{\rm{e}}^{ - \frac{{{t^2}}}{{2{\rm{s}}_{\rm{i}}^2}}}}. $ | (10) |
式中:
对于任意高斯函数
| $ \int\limits_{ - \infty }^{ + \infty } {x(t){\rm{d}}t} = \int\limits_{ - \infty }^{ + \infty } {\hat x{{\rm{e}}^{ - \frac{{{t^2}}}{{2a_0^2}}}}{\rm{d}}t} = \sqrt {2{\rm{ \mathsf{ π} }}} \hat x{a_0}. $ | (11) |
为便于推导,可以假设σ(t)为高斯形式的时域信号,则后向散射截面σ与σ(t)有如下关系
| $ \sigma = \int\limits_{ - \infty }^{ + \infty } {\sigma (t){\rm{d}}t} = \int\limits_{ - \infty }^{ + \infty } {\hat \sigma {{\rm{e}}^{ - \frac{{{t^2}}}{{2s_0^2}}}}{\rm{d}}t} = \sqrt {2{\rm{ \mathsf{ π} }}} \hat \sigma {s_0}. $ | (12) |
式中:
| $ \begin{array}{l} {P_{\rm{s}}}\left( t \right) = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}D_{\rm{r}}^2}}{{4{\rm{ \mathsf{ π} }}\beta _{\rm{t}}^2{R^4}}}{{\hat P}_{\rm{i}}}\sigma \frac{{{s_{\rm{i}}}}}{{\sqrt {s_{\rm{i}}^2 + s_{\rm{0}}^2} }}{{\rm{e}}^{ - \frac{{{{\left( {t - {t_0}} \right)}^2}}}{{2\left( {s_{\rm{i}}^2 + s_{\rm{0}}^2} \right)}}}}\\ \;\;\;\;\;\;\;\; = {{\hat P}_{\rm{s}}}{{\rm{e}}^{ - \frac{{{{\left( {t - {t_0}} \right)}^2}}}{{2s_{\rm{s}}^2}}}}. \end{array} $ | (13) |
式中:t0为激光传输到目标的时间。式(13)表明,激光雷达的回波信号也是一个高斯函数,其中
| $ {\hat P_{\rm{s}}} = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}D_{\rm{r}}^2}}{{4{\rm{ \mathsf{ π} }}\beta _{\rm{t}}^2{R^4}}}{\hat P_{\rm{i}}}\sigma \frac{{{s_{\rm{i}}}}}{{{s_{\rm{s}}}}}. $ | (14) |
如果对回波波形进行积分,可推导出激光雷达回波积分记录值的表达公式如下
| $ \begin{array}{l} \int\limits_{ - \infty }^{ + \infty } {{P_{\rm{s}}}\left( t \right){\rm{d}}t} = \int\limits_{ - \infty }^{ + \infty } {{{\hat P}_{\rm{s}}}{{\rm{e}}^{ - \frac{{{{\left( {t - {t_0}} \right)}^2}}}{{2s_{\rm{s}}^2}}}}{\rm{d}}t} = \sqrt {2{\rm{ \mathsf{ π} }}} {{\hat P}_{\rm{s}}}{s_{\rm{s}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sqrt {2{\rm{ \mathsf{ π} }}} \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}D_{\rm{r}}^2}}{{4{\rm{ \mathsf{ π} }}\beta _{\rm{t}}^2{R^4}}}{{\hat P}_{\rm{i}}}\sigma \frac{{{s_{\rm{i}}}}}{{{s_{\rm{s}}}}}{s_{\rm{s}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{{\eta _{{\rm{atm}}}}{\eta _{{\rm{sys}}}}D_{\rm{r}}^2}}{{4{\rm{ \mathsf{ π} }}\beta _{\rm{t}}^2{R^4}}}\sigma \sqrt {2\pi } {{\hat P}_{\rm{i}}}{s_{\rm{i}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{{\eta _{{\rm{atm}}}}{\eta _{{\rm{sys}}}}D_{\rm{r}}^2}}{{4{\rm{ \mathsf{ π} }}\beta _{\rm{t}}^2{R^4}}}\sigma \int\limits_{ - \infty }^{ + \infty } {{P_{\rm{i}}}\left( t \right){\rm{d}}t} . \end{array} $ | (15) |
式中:
将式(5)、式(7)代入式(14)和式(15),可得到目标回波波形峰值和回波波形积分值与目标地物的BRDF的关系如下:
| $ {\hat P_{\rm{s}}} = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}\pi D_{\rm{r}}^2}}{{4{R^2}}}{\hat P_{\rm{i}}} < f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) > \cos {\theta _{\rm{s}}}\frac{{{s_{\rm{i}}}}}{{{s_{\rm{s}}}}}, $ | (16) |
| $ {E_{\rm{s}}} = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}{\rm{ \mathsf{ π} }}D_{\rm{r}}^2}}{{4{R^2}}}{E_{\rm{i}}} < f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) > \cos {\theta _{\rm{s}}}. $ | (17) |
式(16)中的si / ss表征回波波形的展宽。理论上,目标的粗糙度、地形起伏、入射角度以及光斑大小等因素都将导致波形展宽[10],但是在小光斑激光雷达应用中,只有当展宽超过距离探测分辨率时才能被记录下来。所以当光斑足够小,且没有多次回波的情况下,一般可认为si / ss = 1,回波波形未展宽。
从式(16)、式(17)可知,当其他外部因素不变时,目标的激光雷达回波强度数据(采用回波波形峰值或者回波波形积分值记录)与目标的BRDF、出射角的余弦cosθs以及传输距离1/R2线性相关。
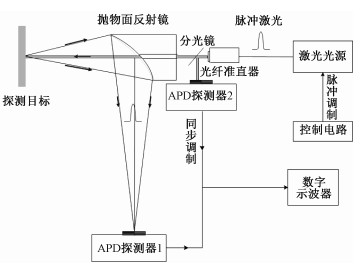
2 激光雷达回波强度数据辐射特性分析与实验验证 2.1 实验平台概述本文利用如图 1所示的实验平台进行激光雷达回波强度数据辐射特性的分析与验证。
|
Download:
|
| 图 1 激光雷达回波强度辐射特性实验平台示意图 Fig. 1 Experimental system of LiDAR echo intensity | |
实验平台中,控制电路发出脉冲调制信号控制激光器发出特定频率的脉冲激光信号,经过准直光路准直发出,照射在目标上经后向散射返回;激光回波信号被接收光路中的抛物面反射镜聚焦接收,传输到雪崩光电二极管(avalanche photo diode,APD)探测器1进行光电转换;同时,激光发射光路通过分光镜得到的激光发射信号传输到APD探测器2,用以对APD探测器1输出的回波电信号进行同步调制,获得发射波与接收波的时间差以及传输距离等信息;为实时显示和观察激光雷达回波信号波形,实验平台中采用数字示波器直接显示/处理/记录APD探测器输出的激光雷达回波波形数据。
该实验平台的主要技术参数如下:激光波长为1 064 nm;激光脉冲重复频率约为30 kHz,脉冲宽度为2 ns(半功率带宽);激光发散角约为0.5 mrad,有效测量距离为5~40 m,在30 m处测量的激光光斑直径约为1.5 cm;记录采样速率为1 ns采样5个点。
表 1列出目前常见的4种全波形激光雷达系统技术参数。可以看出,本文所采用的实验平台与表 1中所列的激光雷达系统的主要参数除有效测量距离外基本相符。因此,本文对于目标反射率、记录方式、观测角度、系统噪声等因素的分析与验证将利用该实验平台进行,而对于距离因素的分析与实验验证将采用商业激光雷达系统VZ-2000i进行。这些研究结论将为基于激光雷达回波强度数据开展定量化参数反演提供支持。
|
|
表 1 常见全波形激光雷达系统参数 Table 1 System parameters of full-waveform LiDAR |
前文的激光雷达辐射机理研究表明:激光雷达后向散射回波强度表征目标的BRDF反射特性,以及它们之间的定量关系。但是在实际应用中,为便于测量和比对,一般用二向性反射率因子(bidirectional reflectance factor,BRF)表征目标的反射特性,理想漫反射体的BRF[11]在数值上为BRDF的π倍:
| $ R\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) = {\rm{ \mathsf{ π} }}f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right), $ | (18) |
式中:R(θi, ϕi, θs, ϕs)表示目标BRF。对于理想漫反射目标,R(θi, ϕi, θs, ϕs) = Rd为常数。当激光雷达回波强度采用回波信号峰值或者回波波形积分值记录时,式(16)、式(17)又可表示为式(19)和式(20),可以看出:激光雷达回波强度数据与漫反射目标的BRF仍然保持线性相关。
| $ {\hat P_{\rm{s}}} = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}D_{\rm{r}}^2}}{{4{R^2}}}{\hat P_{\rm{i}}}{R_{\rm{d}}}\cos {\theta _{\rm{s}}}\frac{{{s_{\rm{i}}}}}{{{s_{\rm{s}}}}}, $ | (19) |
| $ {E_{\rm{s}}} = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}D_{\rm{r}}^2}}{{4{R^2}}}{E_{\rm{i}}}{R_{\rm{d}}}\cos {\theta _{\rm{s}}}. $ | (20) |
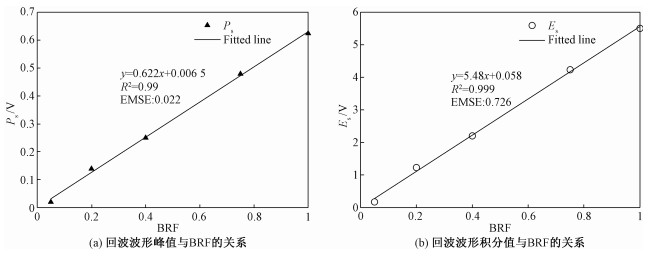
为验证上述理论推导的正确性,采用本文搭建的实验平台,在距离R = 30 m处垂直于入射激光(激光入射角θi为0°)分别放置具有不同反射率(BRF分别为5%、20%、40%、75%和100%,大小为0.5 m×0.5 m)的漫反射板作为目标,采集不同反射率目标的激光回波信号。
为抑制噪声影响,在同一条件下采集20组回波信号(后文采用实验平台开展的验证实验均采集20组数据,不再赘述),然后计算不同反射率目标板的回波波形峰值和回波波形积分值的均值,并分别建立采用回波波形峰值和回波波形积分值这两种记录方式的回波强度与BRF之间的线性拟合关系,结果如图 2所示。
|
Download:
|
| 图 2 实验测量的回波强度与目标反射率的关系 Fig. 2 Relationships between the BRF and the echo intensity | |
图 2中,横坐标表示目标反射率BRF,图 2(a)中的纵坐标表示实验平台测量的回波波形的电压峰值,图 2(b)中的纵坐标表示实验平台测量的回波波形积分值。实验验证在其他因素不变且不考虑噪声影响的条件下,采用回波波形峰值或者回波波形积分值作为激光雷达回波强度记录方式,激光雷达回波强度与目标BRF确实保持线性关系。式(19)、式(20)和实验中使用的BRF漫反射板与传统被动光学遥感中光谱仪测量目标反射率的定义以及辐射定标测量手段相同,这也建立了激光雷达回波强度与传统被动光学目标反射率之间的关系,可以参考被动光学辐射定标的原理标定激光雷达回波强度的辐射特征参数,且标定后的目标反射率在定量遥感应用中与传统被动光学遥感一样具有明确的物理意义。
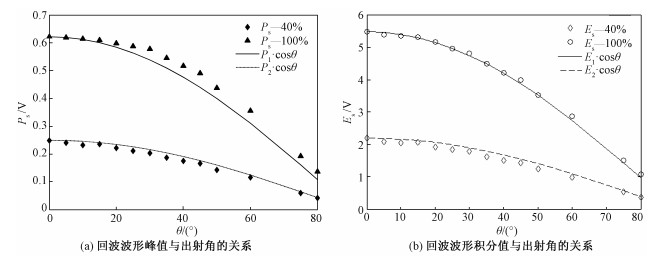
2.3 出射角由式(19)、式(20)可知,在内部外部因素不变或相等条件下,对于同一漫反射目标,无论采用回波信号峰值还是回波信号波形积分值作为激光雷达回波强度记录方式,激光雷达回波强度与出射角θs成余弦关系。
为验证上述理论推导关于回波强度与出射角关系的正确性,采用本文搭建的实验平台,在距离系统30 m处放置漫反射板(取BRF为40%和100%的漫反射板)作为目标,测量和采集激光出射角为0°~80°时的回波信号,然后计算回波波形峰值和回波波形积分值的均值。结果如图 3所示。
|
Download:
|
| 图 3 实验测量的回波强度与激光出射角的关系 Fig. 3 Relationships between the angle and the echo intensity | |
从图中可以看出,在忽略测量误差和噪声等因素的情况下,两种回波强度记录方式都显示出与出射角成余弦关系,这与通过公式推导得到的与出射角余弦cosθs线性相关的结论一致。在实际测量中,采用回波波形积分值作为回波强度的记录方式受上述误差因素影响较小,能够获得更为稳定且接近理论值的结果。对于当前主要激光雷达系统记录的回波强度数据存在出射角不一致的问题,可以利用本文验证的出射角余弦cosθs线性关系进行校正,剔除出射角因素的影响。
进一步分析,如果对式(16)、式(17)进行出射角余弦cosθs影响因素校正,可表示为
| $ \frac{{{{\hat P}_{\rm{s}}}}}{{\cos {\theta _{\rm{s}}}}} = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\rm{atm}}}}{\rm{ \mathsf{ π} }}D_{\rm{r}}^2}}{{4{R^2}}}{\hat P_{\rm{i}}} < f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) > \frac{{{s_{\rm{i}}}}}{{{s_{\rm{s}}}}}, $ | (21) |
| $ \frac{{{E_{\rm{s}}}}}{{\cos {\theta _{\rm{s}}}}} = \frac{{{\eta _{{\rm{sys}}}}{\eta _{{\mathop{\rm atm}\nolimits} }}{\rm{ \mathsf{ π} }}D_{\rm{r}}^2}}{{4{R^2}}}{E_{\rm{i}}} < f\left( {{\theta _{\rm{i}}},{\phi _{\rm{i}}},{\theta _{\rm{s}}},{\phi _{\rm{s}}}} \right) > . $ | (22) |
可以看出:式(21)、式(22)仅校正了出射角影响因素,并没有对目标反射特性进行观测几何条件的归一化处理,消除出射角余弦影响因素后的回波峰值和回波波形积分仍然表征目标的BRDF二向性反射特性。在实际的定量遥感应用中,与传统被动光学遥感类似,也需进一步实施方向校正。该校正不仅与观测几何条件相关,还与激光波长、目标粗糙度等相关。
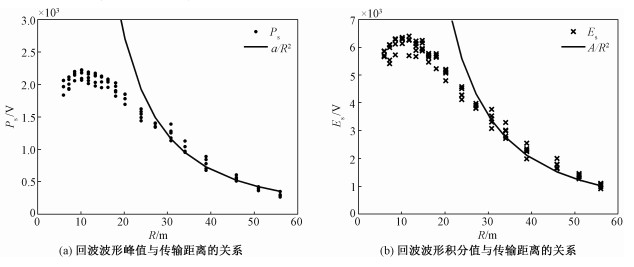
2.4 传输距离由式(19)、式(20)可以得到,对于同一漫反射目标,当出射角一定,回波强度(波形峰值、波形积分值)与传输距离1/R2线性相关。由于本文搭建的实验平台测量距离有限,为更好验证回波强度与传输距离R的关系,本文基于RIEGL公司的全波形激光雷达VZ-2000i,以漫反射参考板(BRF为100%)为目标垂直入射,改变目标到激光雷达的传输距离,采集传输距离R为5~55 m的激光雷达回波波形数据(每个距离处各采集5组数据)。图 4显示以回波波形峰值和回波波形积分值作为记录方式的回波强度与传输距离R的变化关系。
|
Download:
|
| 图 4 VZ-2000i的回波强度与传输距离的关系 Fig. 4 Range vs. intensity for VZ-2000i | |
从图中可见,图 4(a)和4(b)的结果不同于前面实验结果大致与理论推导一致的情况:在近距离处比较不符合规律; 而在距离较远时,如图中所示R>30 m,开始趋近于理论推导的与1/R2的关系。这主要和后向散射的激光接收过程有关,激光传输方程推导过程中,都是假设R→∞的情况,后向散射光接近于平行光入射到接收器,这时后向散射在接收器视场的激光被全部接收,而在近距离处不满足这些条件,所以出现回波强度不满足理论推导的现象。不同的激光雷达系统,回波强度满足1/R2线性关系的临界R值是不同的,因此在实际应用中可以通过预先对系统进行标定,建立回波强度与传输距离R的分段校正函数,来获得准确的回波强度用于后续的定量应用。
2.5 噪声受系统和传输链路噪声的影响,回波信号往往带有噪声。图 5显示实验平台接收到的不同信噪比(signal-to-noise ratio,SNR)水平下的激光雷达回波信号波形。

|
Download:
|
| 图 5 不同信噪比下的激光雷达回波信号波形 Fig. 5 Sample waveforms under different SNR values | |
从图中可以看到,噪声会造成回波信号波形变化、波峰位置偏离, 甚至波形提取困难,并最终影响回波强度的正确性,因此有必要分析噪声对回波强度数据的影响。
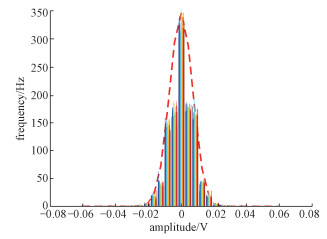
为分析激光雷达噪声特性以及噪声对激光雷达回波信号的影响,本文采用所搭建的实验平台在相同条件下采集100组回波信号Psk(t) (k = 1, 2, …, 100),每组回波信号包含1 000个采样点。以这100组回波信号Psk(t)的波形均值作为无噪声回波信号s(t),将Psk(t)与s(t)相减,则可以得到100组回波噪声信号nk(t),每组噪声信号具有1 000个采用点。对这100组噪声信号nk(t)的所有采样点的幅度值计算其标准差σ为0.01,并做直方图,如图 6所示。
|
Download:
|
| 图 6 回波信号噪声直方图 Fig. 6 Histogram of the noise signal | |
图 6中的红色虚线为按照标准差σ = 0.01、直方图中的最大计数值作为峰值描画的高斯函数曲线;直方图中的不同颜色代表不同组的噪声数据。从图 6可以看到,激光雷达回波信号的噪声幅度值呈现明显的正态分布。说明激光雷达回波信号噪声具有加性高斯白噪声的特征,可以利用高斯白噪声进行模拟分析。
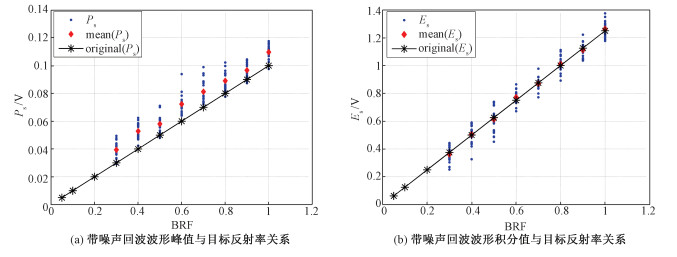
图 7显示采用模拟仿真方式分析得到不同SNR条件下,噪声对回波强度数据的影响。在模拟仿真过程中,模仿相同水平的激光信号垂直照射到具有不同反射率的漫反射目标的情况。故设置回波信号噪声标准差σ均为0.01,与高斯标准差ss = 5、峰值为0.005~0.1 V的高斯信号(模拟BRF为0.3~1的回波信号)相叠加,从而得到对应于不同反射率目标的、具有不同SNR的模拟激光雷达回波信号(为分析噪声影响,生成每种SNR水平的模拟回波信号样本20组)。
|
Download:
|
| 图 7 噪声对激光雷达回波强度数据的影响 Fig. 7 Influence of the noise on the echo intensity | |
图 7中,蓝色点表示20组样本数据的回波波形峰值或者波形积分值;红色点表示20组样本数据的回波波形峰值均值或者回波波形积分值均值;黑色点表示没有噪声的理想回波信号的回波波形峰值或者回波波形积分值。对于目标BRF<0.3的情况,由于模拟回波信号较小,SNR水平低,信号湮没于噪声中无法提取,故没有在图中显示。图 7中,由于回波信号峰值位置根据波形信号最大值的位置取值,故噪声会使得回波信号的波峰位置相对理想无噪声信号的波峰位置发生偏移。对于以回波波形峰值作为回波强度的情况,有噪声情况下的回波强度值通常会大于无噪声时的理想真值,如图 7(a)所示;对于以回波波形积分值作为回波强度的情况,由于积分的平均效应,有噪声情况下的回波强度值会在理想真值附近上下波动,如图 7(b)所示。
表 2给出不同SNR水平下,噪声对激光雷达回波强度数据影响的定量分析结果。表中BRF为0.3~1的数据行与图 7相对应。在仿真分析过程中,设置噪声标准差σ不变,通过改变目标反射率BRF,来改变回波信号强度以及信噪比SNR的大小。表中的SNR定义依据文献[12],公式如下
| $ {\rm{SNR}} = 10{\log _{10}}\frac{{{\rm{DN}}}}{\sigma }. $ | (23) |
|
|
表 2 噪声对激光雷达回波峰值和波形积分值的影响 Table 2 Statistical analysis of the noise |
式中:DN表示无噪声回波信号强度的记录值,σ是噪声信号的标准差。表 2中,统一采用回波波形峰值作为式(23)中的DN进行SNR计算,以对比分析在相同SNR度量下,不同记录方式下噪声对于激光雷达回波强度的影响。
从图 7和表 2可以看出,噪声确实会影响激光雷达回波强度数据的精度,并进而影响后续的定量化应用。采用波形峰值记录回波强度时,噪声的影响明显大于采用波形积分值记录回波强度。当SNR < 10 dB时,回波强度统计误差大于4.5%;随着SNR的增加,噪声的影响逐渐降低,当SNR>17 dB时,回波强度统计误差小于1.5%。因此,当SNR较低(SNR≤17 dB)时,为抑制噪声影响,应尽量采用波形积分值作为激光雷达回波强度的记录方式,并采用多次测量求平均的方式测量回波强度。当SNR>23 dB时,回波强度统计误差小于5‰,无论采用哪种记录方式,噪声的影响均可以忽略。
3 结语随着全波形激光雷达、多光谱/高光谱激光雷达技术的不断发展,激光雷达回波强度信息的定量化应用逐渐成为激光雷达技术领域的前沿热点,开展回波强度数据辐射特性分析可以为其辐射定标和辐射校正方法研究提供理论基础和实践依据,同时也是实现定量化应用的前提。本文从激光雷达辐射传输机理出发,构建具有明确物理意义的激光雷达回波强度数据辐射传输机理方程,基于该方程系统性地探讨和分析激光雷达回波强度数据的辐射特征和关键影响因素,并利用所搭建的小光斑激光雷达实验平台对激光雷达辐射特性进行验证和讨论,得到以下结论:
1) 激光雷达回波强度的两种记录形式——回波波形峰值与回波波形积分值都与目标反射率具有线性关系,采用回波波形积分值作为回波强度的记录方式,受测量、噪声的误差因素影响较小,能够获得更为稳定且接近理论值的结果。
2) 激光雷达回波强度数据(采用回波波形峰值或者回波波形积分值记录)与目标的BRDF、出射角的余弦cosθs以及传输距离1/R2(远距离时,临界R值与激光雷达系统相关)线性相关,但在近距离处与传输距离1/R2不满足这一关系。针对近距离测量的情况,可以建立回波强度与距离的查找表或者是利用函数拟合进行校正。
3) 当SNR < 10 dB时,回波强度统计误差大于4.5%,需要滤波消除噪声的影响;随着SNR的增加,噪声的影响逐渐降低,当SNR较低(SNR≤17 dB)时,为抑制噪声影响,应尽量采用波形积分值作为激光雷达回波强度的记录方式,并采用多次测量求平均的方式测量回波强度;当SNR>23 dB时,回波强度统计误差小于5‰,无论采用哪种记录方式,噪声的影响均可以忽略。
以上研究主要针对影响激光雷达回波强度的外部因素即目标反射特性、目标与激光雷达系统之间的距离、入射/出射角,以及回波强度记录方式、发射与接收过程的噪声这5个因素开展辐射特性分析研究。后续将继续开展大气、波形展宽、光谱等方面的辐射特性分析,从而更全面地分析激光雷达回波强度数据辐射特性,为开展全波形、多光谱/高光谱激光雷达辐射定标、地物分类以及各种定量化应用提供必要的理论依据和技术支持。
| [1] |
Kaasalainen S, Jaakkola A, Kaasalainen M, et al. Analysis of incidence angle and distance effects on terrestrial laser scanner intensity:search for correction methods[J]. Remote Sensing, 2013, 3(10): 2207-2221. |
| [2] |
Schmidt A, Rottensteiner F, Sörgel U. Water-land-classification in coastal areas with full waveform lidar data[J]. Photogrammetrie-Fernerkundung-Geoinformation, 2013(2): 71-81. |
| [3] |
Yan W Y, Shaker A, El-Ashmawy N. Urban land cover classification using airborne LiDAR data:a review[J]. Remote Sensing of Environment, 2015, 158: 295-310. DOI:10.1016/j.rse.2014.11.001 |
| [4] |
谭凯, 程效军, 张吉星. TLS强度数据的入射角及距离效应改正方法[J]. 武汉大学学报(信息科学版), 2017, 42(2): 223-228. |
| [5] |
Xu T, Xu L, Yang B, et al. Terrestrial laser scanning intensity correction by piecewise fitting and overlap-driven adjustment[J]. Remote Sensing, 2017, 9(11): 1090. DOI:10.3390/rs9111090 |
| [6] |
Wagner W. Radiometric calibration of small-footprint full-waveform airborne laser scanner measurements:basic physical concepts[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(6): 505-513. DOI:10.1016/j.isprsjprs.2010.06.007 |
| [7] |
Baltsavias E P. Airborne laser scanning:basic relations and formulas[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2): 199-214. |
| [8] |
Haner D A, Kavaya M J, Flamant P H, et al. Target reflectance measurements for calibration of lidar atmospheric backscatter data[J]. Appl Opt, 1983, 22(17): 2619. DOI:10.1364/AO.22.002619 |
| [9] |
Wagner W, Ullrich A, Ducic V, et al. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(2): 100-112. DOI:10.1016/j.isprsjprs.2005.12.001 |
| [10] |
李磊, 胡以华, 赵楠翔, 等. 激光遥感目标回波脉宽展宽特性实验[J]. 红外与激光工程, 2010, 39(2): 246-250. DOI:10.3969/j.issn.1007-2276.2010.02.012 |
| [11] |
Schaepman-Strub G, Schaepman M E, Painter T H, et al. Reflectance quantities in optical remote sensing:definitions and case studies[J]. Remote Sensing of Environment, 2006, 103(1): 27-42. |
| [12] |
全国遥感技术标准化技术委员会.机载激光雷达点云数据质量评价标准及计算方法: GB/T 36100-2018[S].北京: 中国标准出版社, 2018: 9.
|
 2019, Vol. 36
2019, Vol. 36 


