2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
星载合成孔径雷达(synthetic aperture radar, SAR)具有全天时、全天候的成像能力,能够进行全球高分辨率成像,所以在微波遥感领域发挥着巨大的作用。高分辨率SAR在立体测绘、农业普查、城建勘测、减灾救灾、资源保护、海域动态监测等民用领域以及侦查、监视等军事领域有着不可替代的作用。分辨率越高的图像,从图像中获取的目标特征和场景信息就越丰富,其应用价值就越大。随着技术的不断进步,星载SAR朝着高分辨率、宽测绘带、多极化、多基多模式方向发展[1-4]。星载SAR轨道高度一般在几百公里的位置,SAR信号会两次经过电离层。在低分辨率、较高载频时,电离层对SAR信号的影响较小,可以忽略。但是随着分辨率的不断提高,发射信号的带宽不断增大,电离层对SAR信号的影响较大,相对于系统指标不能忽略。国内外学者对于电离层效应对SAR信号的影响以及电离层误差校正方法进行了大量的研究[5-6], 研究主要集中在低载频如P波段以及较小带宽的情况。Liu等[7]分析甚高频段SAR信号受到电离层的影响,会造成分辨率下降以及图像距离向偏移。Jehle等[8]利用SAR信号带宽较大的特点,提出通过不断改变匹配滤波器的持续时间,寻找脉冲压缩峰值的方法,计算脉冲宽度的变化量。李亮等[9]根据低频段SAR信号受电离层影响的仿真结果,使用有源定标器结合内定标数据计算脉冲宽度变化反演出电离层误差。赵宁等[10-11]分析P波段星载SAR电离层色散效应,并提出一种基于双频SAR距离相关的延迟测量方法用于电离层误差的校正,同时通过步进频ISAR,利用地基P波段雷达对空间目标进行观测以计算电离层TEC值。王成等[12]考虑电离层色散以及电离层多重散色效应造成图像距离向质量下降。苏星伊等[13]仿真P波段电离层对SAR信号的影响,并根据回波利用平移相关法的思想对电离层参数进行估计。
本文首先讨论电离层色散效应及其对星载SAR信号的影响;接着根据时域仿真流程,仿真不同波段、不同带宽和不同TEC条件下,色散效应对SAR回波的影响;最后通过仿真点目标成像分析P、L、C和X在不同带宽条件和TEC下,电离层色散效应对点目标成像质量的影响, 为高分辨率星载SAR系统的设计和误差补偿提供参考。
1 电离层色散效应 1.1 色散效应原理地球大气层可分为低层大气和电离层,电离层位于60~2 000 km这一位置。此区域存在相当多的自由电子和离子,能够较为显著地影响通过此区域电磁波的传播方向、速度、相位等,目前在轨运行的星载SAR系统的轨道高度大都位于这一区域,雷达信号的发射与接收不可避免地要经过电离层。电离层中电磁波传播的折射指数可以表示为Appleton-Hartree公式[14-15],即电磁波在等离子体中传播的色散关系式:
| $ n^{2}=1-\frac{X}{1-\mathrm{j} Z-A \pm B}, $ | (1) |
| $ A=\frac{Y^{2} \sin ^{2} \theta}{2(1-X-\mathrm{j} Y)}, $ | (2) |
| $ B=\sqrt{A^{2}+Y^{2} \cos ^{2} \theta}. $ | (3) |
式中3个参数X, Y和Z,即为Appleton参数,
| $ X=\frac{\omega_{\mathrm{p}}^{2}}{\omega^{2}}, \overline{Y}=\mp \frac{\omega_{\mathrm{H}}}{\omega} \overline{B}, Z=\frac{\nu}{\omega}. $ | (4) |
式中:θ为电波法向和地磁场夹角:ν为自由电子与重粒子碰撞频率;ωp是等离子体频率,ωH是磁旋频率,其表达式为
| $ \omega_{\mathrm{H}}=\left|\frac{e B_{0}}{m}\right|, \omega_{\mathrm{p}}^{2}=\frac{e^{2} N_{\mathrm{e}}}{m \varepsilon_{0}}. $ | (5) |
式中:B0为地磁场强度,e为电子电量,m为电子质量,Ne为电子浓度,ε0为真空中介电常数。当频率大于300 MHz、并忽略磁离子射线裂变时,式(1)可简化为
| $ n \approx 1-f_{\mathrm{p}}^{2} /\left(2 f^{2}\right). $ | (6) |
从式(6)可以看出,折射指数是频率的数,电离层介质是一种色散介质,电磁波传播的群速度不一定等于相速度。
1.2 色散效应对星载SAR信号的影响 1.2.1 色散效应对距离向的影响电离层色散对SAR信号传播的影响主要从以下两个方面考虑[16]:
1) 电离层色散对信号相位的影响:磁波传播有效相路径长度为
| $ R=\int_{L} n \mathrm{d} l, $ | (7) |
式中L表示的是信号传播路径。电离层色散效应引入的相路径长度变化ΔRp:
| $ \Delta R_{\mathrm{p}}=\int_{L}(n-1) \mathrm{d} l=-\frac{K}{f^{2}} \cdot \mathrm{TEC}. $ | (8) |
式中K=40.28 m3/s2,TEC(total electroni content)为电离层电子总量,由式(8)可知,色散效应导致相路径长度变短,相对于自由空间会对信号附加一个双程超前相位
| $ \Delta \varphi (f) = 2\pi \cdot \frac{{\left| {\Delta {l_{\rm{p}}}} \right|}}{\lambda } = \frac{{4{\rm{ \mathsf{ π} }}K}}{{cf}}{\rm{TEC}}{\rm{.}} $ | (9) |
2) 色散效应对信号传播时间的影响:在色散介质中,电磁波的群速度不等于相速度,由此引入的群路径变化量ΔRg:
| $ \Delta {R_{\rm{g}}} = \int_L {\left( {\frac{1}{n} - 1} \right)} {\rm{d}}l \cong - \Delta {R_{\rm{p}}} = \frac{K}{{{f^2}}}{\rm{TEC}}{\rm{.}} $ | (10) |
由(8)可知,色散效应导致群路径变长,由此引入的信号双程传播时延Δt为
| $ \Delta t = \frac{{2\Delta {R_{\rm{g}}}}}{c} = \frac{{2K}}{{c{f^2}}}{\rm{TEC}}. $ | (11) |
为分析附加的超前相位对信号的影响,将式(9)在载频处进行Taylor展开
| $ \begin{array}{*{20}{c}} {\Delta {\varphi _{\rm{r}}}(f) = 4{\rm{ \mathsf{ π} }}\frac{{K \cdot {\mathop{\rm TEC}\nolimits} }}{c}\left( {\frac{1}{{{f_0}}} - \frac{{f - {f_0}}}{{f_0^2}}} \right) + }\\ {4{\rm{ \mathsf{ π} }}\frac{{K \cdot {\mathop{\rm TEC}\nolimits} }}{c}\sum\limits_{n = 2}^{ + \infty } {{{( - 1)}^n}} \frac{{{{\left( {f - {f_0}} \right)}^n}}}{{f_0^{n + 1}}}.} \end{array} $ | (12) |
式中: |f-f0|≤B/2,f0是发射信号的载频,B是发射信号的带宽。括号内常数项对成像没有影响,一次项变换到时域后经过脉冲压缩会产生距离向的偏移,偶数阶相位误差会导致信号的主瓣展宽、峰值点能量下降和旁瓣升高,奇数阶相位误差的存在导致点目标脉冲压缩后旁瓣不对称畸变,高阶相位的影响取决于相对带宽的大小。
1.2.2 色散效应对方位向的影响电离层电子总量TEC又称电离层电子浓度柱含量、积分含量等,其定义为以单位面积为底面积,信号贯穿整个电离层传播路径为高的柱体中所包含的总电子数
| $ {\rm{TEC}} = \int_{{h_{{\rm{eo}}}}}^{{h_{\rm{T}}}} {{N_e}} {\rm{d}}l. $ | (13) |
式中: Ne为电子浓度,l为信号传播路径,heo为电离层下边界高度,hT为柱体的上顶高度。由于电子浓度与高度有关,电离层TEC值具有空变性。
由于SAR成像过程中点目标方位向回波经历的斜距TEC随着方位位置的变化,导致背景电离层对距离压缩的影响存在随着方位位置的变化。斜距TEC[17]可表示为
| $ {\mathop{\rm TEC}\nolimits} (x) = \frac{{{{{\mathop{\rm TEC}\nolimits} }_{\rm{V}}}}}{{\cos {\theta _0}}}\frac{{\sqrt {R_0^2 + {x^2}} }}{{{R_0}}}, $ | (14) |
式中:x为SAR当前时刻的方位位置,TECV是天线高度到地面垂直方向的TEC,R0为最短斜距。那么在合成孔径时间内,传播路径上的最大TEC变化量为合成孔径边缘与合成孔径中心处TEC之差,其值为
| $ \Delta {\rm{TEC}} = \frac{{{\rm{TE}}{{\rm{C}}_{\rm{v}}}}}{{\cos {\theta _0}}}\left( {\frac{{\sqrt {R_0^2 + \left( {{L_a}/2} \right)} }}{{{R_0}}} - 1} \right). $ | (15) |
由于TEC随方位位置变化,对方位向成像的影响主要有两方面:造成距离徙动误差;引入附加相位误差。距离徙动误差可表示为
| $ \begin{array}{*{20}{c}} {\Delta {R_{\rm{c}}} = \sqrt {R_0^2 + {X^2}} + \frac{{K \cdot {\mathop{\rm TEC}\nolimits} (x)}}{{f_0^2}}}\\ { - \sqrt {{{\left( {{R_0} + \frac{{K \cdot {\rm{TE}}{{\rm{C}}_{\rm{v}}}}}{{f_0^2}}} \right)}^2} + {x^2}} ,} \end{array} $ | (16) |
引入的附加相位为
| $ \Delta \varphi \left( x \right) = \frac{{4{\rm{ \mathsf{ π} }}K \cdot {\rm{TEC}}\left( x \right)}}{{\lambda f_0^2}}. $ | (17) |
SAR一般发射的是经过调制的线性调频脉冲,在脉冲持续时间内,频率与时间成正比。由于电离层是色散介质,不同频率的信号经过电离层时,信号双程时延各不相同,脉冲起始和截止频率带来的附加时延[15]为:
| $ {t_{\rm{s}}} = \frac{{2K \cdot {\rm{TEC}}}}{{cf_{\rm{s}}^2}},{t_{\rm{e}}} = \frac{{2K \cdot {\rm{TEC}}}}{{cf_{\rm{e}}^2}}. $ | (18) |
由式(18)可得,SAR接收到的回波脉冲宽度变化量为Δtp=te-ts。对于负调频信号fs>fe,脉冲宽度被展宽;对于正调频信号fs<fe,脉冲宽度被压缩。接收信号的调频率等效为Kr′=B/(tp+Δtp),B为信号带宽。
假设SAR发射的理想线性调频信号为
| $ \begin{array}{l} {s_0}(\tau ,\eta ) = {A_0}{w_{\rm{r}}}(\tau ){w_{\rm{a}}}(\eta ) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}{f_0}\tau } \right)\exp \left( {{\rm{j \mathsf{ π} }}{K_{\rm{r}}}{\tau ^2}} \right) \end{array} $ | (19) |
经过解调后理想目标回波信号为:
| $ {s_0}(\tau ,\eta ) = {A_0}{w_{\rm{r}}}{w_{\rm{a}}}\exp \left( {{\rm{j}}{\varphi _{\rm{a}}}} \right)\exp \left( {{\rm{j}}{\varphi _{\rm{r}}}} \right), $ | (20) |
| $ {\varphi _a} = \frac{{4{\rm{ \mathsf{ π} }}{f_0}R(\eta )}}{c},{\varphi _{\rm{r}}} = {\rm{ \mathsf{ π} }}{K_{\rm{r}}}{\left( {\tau - \frac{{2R(\eta )}}{c}} \right)^2}. $ | (21) |
式中:A0为一个复常数,τ为距离向时间,η为方位向时间,Kr为距离向调频率,wr和wa分别为距离向和方位向窗函数。
雷达发射电磁波往返两次经过电离层,当考虑电离层的影响时,雷达接收到的回波在距离频域可表示为
| $ S_{\rm{r}}^\prime \left( {{f_r},\eta } \right) = {S_{\rm{r}}}\left( {{f_{\rm{r}}},\eta } \right)\exp \left( {{\rm{j}}\Delta \varphi \left( {{f_{\rm{r}}}} \right)} \right). $ | (22) |
式中: fr为距离频率,fr∈[-B/2, B/2],sr(fr, η)为理想信号回波距离频域表达式。综合以上分析,实际仿真步骤如下:
步骤1:设置电离层TEC值;
步骤2:根据系统仿真参数和TEC值,计算色散效应带来的双程超前相位;
步骤3:在距离频域将理想信号与附加的超前相位相乘受电离层影响的频域信号;
步骤4:将频域信号进行IFFT。
实际仿真流程如图 1所示。

|
Download:
|
| 图 1 仿真流程图 Fig. 1 Flowchart of simulation | |
根据仿真流程,对电离层色散效应影响下的点目标进行仿真,首先分析距离偏移量和峰值相位误差与系统参数的关系,然后进行点目标仿真,最后通过成像质量指标的计算对仿真结果进行分析。
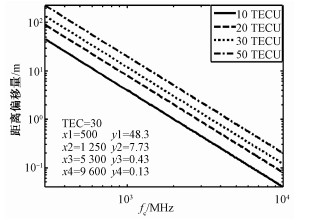
2.2.1 距离向偏移附加的超前相位中含有一阶相位,由傅里叶变换的性质可知,一阶相位导致回波经过脉冲压缩后产生距离向的偏移,距离偏移量为:ΔL=K·TEC/f02。距离偏移量与发射信号的载频和电离层TEC值有关,从图 2可以看出随着载频的升高,距离偏移迅速减小。以30TECU为例,在P波段载频500 MHz时,距离偏移超过48 m,而在X波段9.6 GHz时,距离偏移量也达到0.13 m。对于高分辨星载SAR,该值会对场景中目标的几何定位带来较大误差,必要时需进行几何校正。
|
Download:
|
| 图 2 信号载频与距离向频移量的关系 Fig. 2 Relationship between signal carrier frequency and distance offset | |
相位误差的存在会导致图像的成像质量恶化, 该值随着频率和带宽变化。为研究其对成像的影响,当满足|f-f0|=B/2时,相位误差达到最大,其值为
| $ \Delta {\varphi _N} = 4{\rm{ \mathsf{ π} }}K \cdot {\rm{TEC}} \cdot \sum\limits_{n = 1}^N {{{( - 1)}^n}} {(B/2)^n}/\left( {cf_0^{n + 1}} \right). $ | (23) |
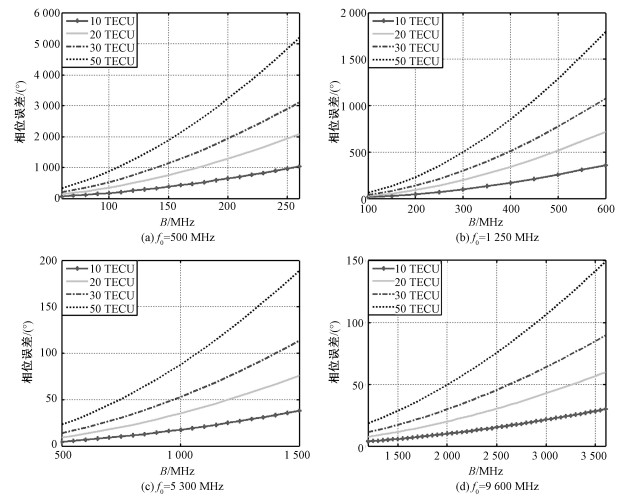
计算峰值相位误差需要考虑N值,在仿真过程中设置相位误差阈值,当展开的第N+1阶相位误差小于1°时即可忽略N阶以上相位误差,该阈值能够满足精度要求。同时对于一阶相位其值仅影响目标距离向的位置,对成像质量并没有影响,计算相位误差时只考虑非线性相位误差。仿真时选取4个不同的载频、不同TEC值下,峰值相位误差随信号带宽变化结果如图由式(6)可知,信号传播的相折射指数大于1且该值随频率增加而减小,导致相路径变短,在接收的回波中引入与频率相关的超前相位。相位误差过大会导致分辨率下降、峰值旁瓣比和积分旁瓣比升高。从图 3可以看出,随着载频的升高相位误差会迅速减小,P波段相位误差较大,当带宽为100 MHz、TEC为30 TECU时,相位误差达到400°,这会严重影响成像的质量。对于高分辨率星载SAR,一般工作在X波段,例如美国在轨运行的“长曲棍球”SAR卫星工作载频10 GHz,据报道其最高分辨率达0.15 m,系统带宽达2 GHz,当TEC值超过50 TECU时,相位误差峰值已超过π/4,电离层色散对星载SAR成像的影响必须予以考虑。
|
Download:
|
| 图 3 峰值相位误差与带宽的关系 Fig. 3 Relationship between peak phase error and bandwidth | |
电离层色散附加的相位误差与信号载频、带宽以及TEC值有关,因此仿真电离层色散效应在不同载频、不同带宽和不同电离层TEC值条件下对点目标聚焦的影响。仿真参数见表 1。点目标成像仿真结果见图 4。同时对点目标聚焦效果进行分析,其结果见表 2。
|
|
表 1 距离向仿真参数 Table 1 Range simulation parameters |

|
Download:
|
| 图 4 电离层色散对点目标距离向成像的影响 Fig. 4 Influence of ionospheric dispersion on point target range imaging | |
|
|
表 2 点目标距离向聚焦性能分析 Table 2 Performance analysis of point target range focusing |
电离层群折射指数为
1) 随着载频的升高,距离向偏移迅速减小;随着TEC值增加,偏移量也会增加。
2) 信号载频不同,电离层色散效应对点目标的影响出现较大的差异,影响程度与信号带宽载频比密切相关。P波段、L波段信号受到电离层色散效应的影响较大,当带宽载频比为0.2,TEC值超过30 TECU时,点目标已无法聚焦。C波段和X波段点目标带宽载频比为0.4时,若要聚焦良好,在不进行误差校正时,则TEC值不能超过10 TECU。
3) 信号载频一定时,随着带宽和TEC值的增加,电离层影响会变大,峰值旁瓣比和积分旁瓣比升高,峰值点能量和分辨率下降,严重时无法聚焦。
通过TEC现报可知,中国大部分地区电离层TEC值介于15~35 TECU之间。对于P波段和L波段信号而言,带宽载频比不宜超过0.1,C波段和X波段信号的带宽载频比不宜超过0.3,否则需要补偿电离层色散效应带来的误差。表 3是一些在轨的不同波段星载SAR和不同带宽载频比时,对电离层的容忍度,通过该表可以评估电离层色散影响是否需要校正。
|
|
表 3 不同载频和带宽载频比时,二次相位误差(TEC=50 TECU) Table 3 QPE values at different carrier frequencies and bandwidth carrier ratios |
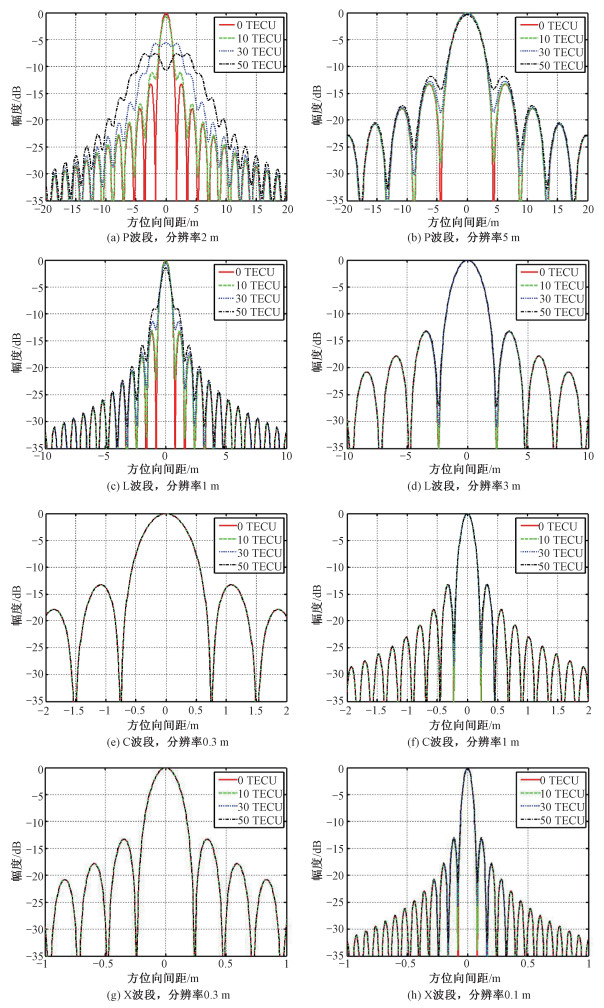
电离层TEC值随着方位位置的变化而变化,对于高分辨率SAR而言,由于合成孔径时间大大增加,电离层TEC在整个合成孔径内的变化将增加,近而导致电离层引入的方位向相位误差增大。通过仿真不同载频和不同分辨率下电离层色散对点目标方位向聚焦的影响。仿真参数见表 4。方位向点目标仿真结果如图 5,性能分析见表 5。
|
|
表 4 方位向仿真基本参数 Table 4 Azimuth simulation parameters |
|
Download:
|
| 图 5 电离层色散对点目标方位向成像的影响 Fig. 5 Influence of ionospheric dispersion on point target azimuth imaging | |
|
|
表 5 点目标方位向聚焦性能分析 Table 5 Performance analysis of point target azimuth focusing |
电离层色散对方位向的影响主要是由于在合成孔径时间内传播路径不同导致TEC变化,合成孔径时间越长TEC的变化量就越大,导致电离层色散引入的斜距误差随方位位置而改变,从而影响方位向成像效果。从图 5和表 5可以看出,在载频一定时,分辨率越高,合成孔径时间越长,电离层色散对方位向聚焦的影响越大;当分辨率相同时,随着载频的升高,电离层色散对方位向聚焦的影响会不断地降低,P波段和L波段信号,更易受电离层色散的影响;分辨率和载频一定时,随着TEC的增加,电离层色散对方位聚焦的影响也会变大,电离层TEC值不超过35 TECU时,在给定的分辨率中,L波段、C波段、X波段聚焦效果良好。
3 总结本文通过对星载SAR电离层色散效应建模和仿真,分析不同载频、不同带宽和不同电离层TEC值, 电离层色散效应对星载SAR距离向和方位向成像的影响。通过仿真结果看出P波段和L波段,电离层色散效应对信号方位向和距离向聚焦的影响较为明显,必要时需要进行误差校正;C波段和X波段,当带宽载频比高于0.3时,也需考虑电离层色散对距离向聚焦的影响。低波段星载SAR具有较强的穿透能力,而高波段星载SAR有利于实现高分辨,通过分析不同波段和不同带宽时,电离层色散对SAR信号的影响,能够为星载SAR系统设计和参数选择提供参考,并有助于电离层色散效应校正方法的研究。
| [1] |
邓云凯, 赵凤军, 王宇. 星载SAR技术发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1-10. |
| [2] |
崔丽萍, 王晓青. SAR影响建筑物震害检测方法研究综述[J]. 震灾防御技术, 2016, 11(2): 239-250. |
| [3] |
范剑超, 王德毅, 赵建华, 等. 高分三号SAR影像在国家海域使用动态监测中的应用[J]. 雷达学报, 2017, 6(5): 456-472. |
| [4] |
王岩飞, 刘畅, 詹学丽, 等. 无人机载合成孔径雷达系统技术与应用[J]. 雷达学报, 2016, 5(4): 333-349. |
| [5] |
Belcher D P. Ionospheric effects on synthetic aperture radar clutter statistics[J]. IET Radar, Sonar&Navigation, 2013, 7(9): 1004-1011. |
| [6] |
Cao P, Xing M D, Sun G C, et al. Minimum entropy via subspace for ISAR autofocus radar[J]. Geoscience and Remote Sensing Letters, 2010, 7(1): 205-209. |
| [7] |
Liu J, Kuga Y, Ishimaru A. Ionospheric effects on SAR imaging:a numerical study[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41: 937-947. |
| [8] |
Jehle M, Frey O, Small D, et al. Measurement of ionospheric TEC in spaceborne SAR data[J]. IEEE Trans Geosci, RemoteSens, 2010, 48(6): 2460-2468. DOI:10.1109/TGRS.2010.2040621 |
| [9] |
李亮, 洪峻, 明峰, 等. 一种基于有源定标器的电离层对星载SAR定标影响校正方法[J]. 电子与信息学报, 2012, 34(5): 1096-1101. |
| [10] |
赵宁, 谈璐璐, 张永胜, 等. 星载P波段SAR电离层效应的双频校正方法[J]. 雷达科学与技术, 2013, 11(3): 255-261. DOI:10.3969/j.issn.1672-2337.2013.03.006 |
| [11] |
赵宁, 周芳, 王震, 等. P波段雷达成像电离层效应的地面观测与校正[J]. 雷达学报, 2014, 3(1): 45-52. |
| [12] |
王成, 张民, 许正文, 等. 基于星载SAR信号的TEC反演新方法[J]. 地球物理学报, 2014, 57(11): 3570-3576. DOI:10.6038/cjg20141110 |
| [13] |
苏星伊, 邢孟道, 周芳, 等. SAR成像中电离层的影响估计及其补偿[J]. 中国科技论文, 2016, 11(14): 1600-1604. DOI:10.3969/j.issn.2095-2783.2016.14.009 |
| [14] |
Xu Z W, Wu J, Wu Z S. A survey of ionospheric effects on space-based radar[J]. Waves in Random Media, 2004, 14(2): S189-S273. DOI:10.1088/0959-7174/14/2/008 |
| [15] |
焦培南, 张忠治. 雷达环境与电波传播特性[M]. 北京: 电子工业出版社, 2007.
|
| [16] |
姚佰栋, 时晶晶. 电离层对星载P波段合成孔径雷达成像的影响[J]. 无线互联科技, 2015(5): 139-142. DOI:10.3969/j.issn.1672-6944.2015.05.062 |
| [17] |
李力.星载P波段合成孔径雷达中的电离层效应研究[D].长沙: 国防科学技术大学, 2014.
|
 2019, Vol. 36
2019, Vol. 36 


