2. 中国科学院电子学研究所, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着全球经济的高速发展,人类对于能源的需求在不断增加,过量使用储量有限的化石能源对全球生态环境造成十分严重的破坏。相比之下,太阳能不仅清洁安全无污染,而且具有储量大可再生的特点[1]。目前已发现的化石能源储量仅为同年太阳照射到地表能量的不足万分之一[2]。通过太阳追踪技术高效利用太阳能源可以有效解决能源和环境问题,而太阳追踪技术的提高需要更加准确且高效的太阳位置计算。
准确而高效的太阳位置计算在微光载荷辐射定标和验证、微光载荷定标处理系统研制等工程项目中应用广泛。尤其当参与辐射定标的卫星在晨昏时刻成像时,太阳光线受大气折射影响严重,传统太阳位置算法对此考虑不足,同时也忽略了地球长短半径不同对于太阳位置计算带来的误差。只有在保持简便高效的同时提高太阳高度角的计算精度,才能满足大气海洋环境相关探测、空间环境检测、森林防灾、遥感辐射定标等科研与工程项目的需求。
太阳高度角的计算离不开太阳赤纬角和太阳时角,国内外学者对此做了相关研究。在太阳赤纬角方面,前人的研究给出过相关算法[3-7]。在太阳时角方面,也有研究者介绍过相关算法[4-5, 7-9]。但上述算法多是针对不同年份使用系数相同的计算公式,以地球为球体模型进行研究,对于地球长短半径差别、太阳光线经过大气折射所产生的蒙气差等因素没有充分考虑。此外,还有研究者介绍过几种复杂算法[10-13]。复杂算法尽管精度提升,但编程计算量大,效率不高,适用年份有限,每隔一段时间需要重新修改相关公式,适用于天文学研究,而不利于应用在需要简洁高效计算太阳位置的工程领域。
本文在上述研究的基础上,首先通过数值拟合法提出一种更加适用于不同年份的太阳赤纬角改进算法,然后根据误差曲线体现的周期性规律,以4年为一个周期,提出基于傅里叶展开法的太阳赤纬角改进公式,上述改进公式可根据不同年份周期调整相关系数。随后针对地球球体模型对于长短半径差异考虑不足的问题,推导出太阳高度角在地球椭球模型中的改进公式,并且考虑大气折射在低仰角条件下对于光线路径的影响,使用拟合法和展开法分段给出蒙气差常差以及附加系数在0°~30°仰角下的改进算法。随后计算并对比本文所提出的改进算法与相应的传统算法之间的误差,根据计算结果提出具有更高精度同时高效简洁的太阳位置算法。
1 太阳赤纬角改进公式和时差误差分析 1.1 太阳高度角相关概念太阳高度角是指太阳直射到地表的光线与之在地平面上的投影线之间的夹角,这一定义原本比较成熟[14]。不过在传统太阳位置算法中,地球模型被当作简单球体,根据球面三角公式推导出太阳高度角公式。而地球椭球模型则主要应用在大地测量学、地图学的相关研究中,在太阳地球位置计算方面研究有限。
太阳赤纬角指的是太阳和地球中心连线方向与赤道平面的夹角,太阳时角是指太阳所在的时圈与通过观测点的子午圈组成的二面角[15]。太阳赤纬角和时角的计算精度直接影响太阳高度角的计算准确性。
1.2 几种常见的太阳赤纬角算法Cooper[3]给出太阳赤纬角的求解算法:
| $ \delta=23.45 \sin \left(2 \pi \frac{284+n}{365}\right). $ | (1) |
式中,n为所求日期在该年中的计日序数,如某年1月9日,n=9。
Spencer[4]提出太阳赤纬角算法
| $ \begin{array}{l} \delta = 0.006918 - 0.399912\cos (\theta ) + \\ \;\;\;\;\;\;0.070257\sin (\theta ) - 0.006758\cos (2\theta ) + \\ \;\;\;\;\;\;0.000907\sin (2\theta ) - 0.002697\cos (3\theta ) + \\ \;\;\;\;\;\;0.00148\sin (3\theta ). \end{array} $ | (2) |
式中:θ为日角,
Stine[5]提出太阳赤纬角算法
| $ \delta = {\sin ^{ - 1}}\left[ {0.39795\cos \left( {2{\rm{ \mathsf{ π} }}\frac{{n - 173}}{{365.242}}} \right)} \right]. $ | (3) |
式中:n为所求日期在一年中的计日序数。该算法所求出的结果亦为弧度制。
Bourges[6]给出太阳赤纬角算法
| $ \begin{aligned} \delta=& 0.3723+23.2567 \sin (\omega t)+\\ & 0.1149 \sin (2 \omega t)-0.1712 \sin (3 \omega t)-\\ & 0.7580 \cos (\omega t)+0.3656 \cos (2 \omega t)+\\ & 0.02010 \cos (3 \omega t), \end{aligned} $ | (4) |
式中:ω为参考弧度系数,取
| $ \begin{aligned} n_{0}=& 78.801+[0.2422(n-1969)]-\\ & \text { int }[0.25(n-1969)]. \end{aligned} $ |
Yu[7]针对Spencer算法进行一定简化,提出太阳赤纬角算法
| $ \begin{array}{l} \delta = 0.006918 - 0.399912\cos (\theta ) + \\ \;\;\;\;\;\;0.070257\sin (\theta ) - 0.006758\cos (2\theta ) + \\ \;\;\;\;\;\;0.000907\sin (2\theta ) \end{array} $ | (5) |
式中:θ为日角,
本文结合天文年历记录的太阳赤纬角数据,在Windows系统中以Matlab为工具进行计算,得到上述不同赤纬角算法的误差变化情况。在此以2017年为例,给出该年内不同算法每天误差的变化情况,如表 1所示。Bourges太阳赤纬角算法在2017年的误差均方根为0.011 16°,最大值为0.025°,在传统算法中误差最小。王炳忠[16]沿用该公式,并且对于积日n0做了细微修正,并在这一基础上对于日地距离的计算提出其他观点,如果仅从太阳赤纬角的计算考虑,Bourges的公式也可以称为Wang法。
|
|
表 1 2017年不同太阳赤纬角算法误差对比 Table 1 Error comparison of different solar declination algorithms in 2017 |
上述所有方法中,对于不同年份的计算采用的是系数相同的公式,未充分考虑太阳赤纬角在不同年份存在差异和变化的问题。本文在保持太阳赤纬角计算过程简便的同时,以降低计算误差为目的,提出可以针对不同年份调整相关系数的计算公式,随后通过具体的计算比较,验证改进算法对于改进太阳赤纬角精度具有优势。
1.3 数值拟合法计算太阳赤纬角首先采用数值拟合法,针对需要研究的年份,以该年度天文年历记录的太阳赤纬角为基础,对于太阳赤纬角和积日因子β进行多项式拟合,积日因子β是可以根据需求年份和计日序数进行调整的中间变量,得到适用不同年份的拟合系数。太阳赤纬角改进公式可以表达为
| $ \begin{array}{l} {n_0} = 79.6764 + 0.2422(n - 1985) - \\ \;\;\;\;\;\;\;{\mathop{\rm int}} (n - 1985),\\ \;\;\;\;\;\;\;\;\;\;\;\beta = \frac{{2\pi \left( {{d_n} - 1 - {n_0}} \right)}}{{365.2422}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta = \sum\limits_{k = 0}^{11} {{a_k}} {\beta ^k}. \end{array} $ | (6) |
式中:n为年份数;dn为一年中的计日序数;ak为拟合系数。若需要天文年历没有记录的时刻的太阳赤纬角数据,可以采用贝塞尔插值法求解。表 2为本文太阳赤纬角拟合法中具体到每一年的系数,在此以适用于2015—2018年的系数进行列举。
|
|
表 2 2015—2018年太阳赤纬角拟合系数 Table 2 Fitting coefficients of solar declination from 2015 to 2018 |
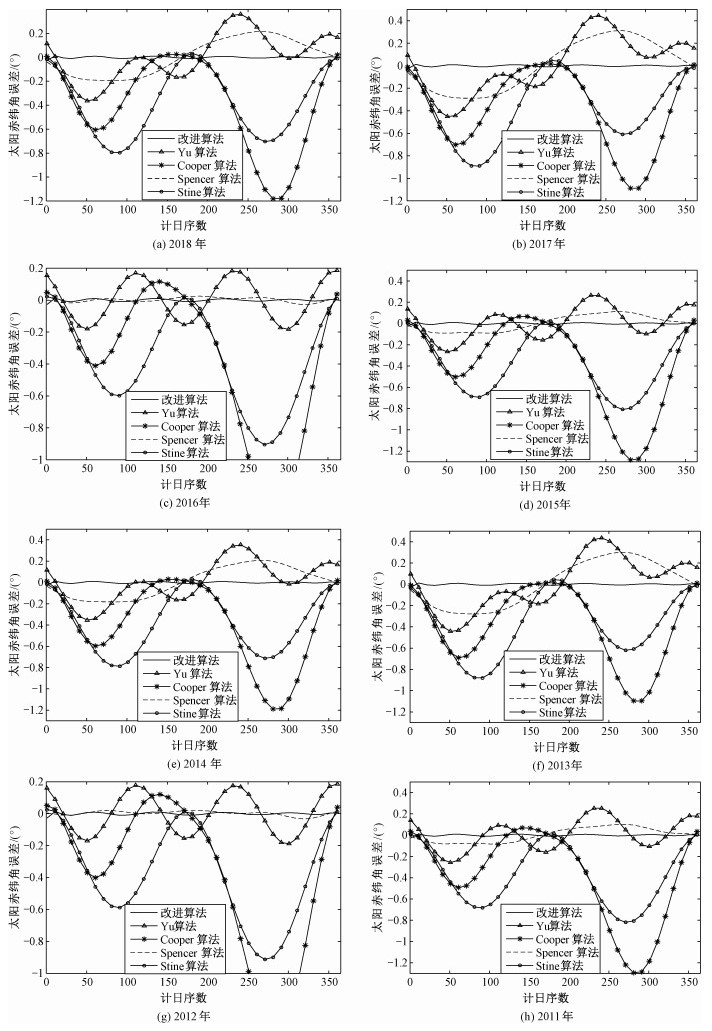
为直观显示改进算法与传统算法误差的对比,本文对本世纪所有年份太阳赤纬角进行误差计算,并选取2011—2018年给出误差对比曲线。在图 1中,不同曲线表示不同算法的计算误差,实线代表本文算法的误差在一年内变化情况。结果显示,本文给出的拟合算法的误差均值和波动范围均明显小于传统算法,对于降低误差效果显著。更重要的是,通过不同年份误差曲线组合对比发现,不同算法误差的变化趋势呈现出明显的周期性,以4年为一个周期,不同周期内相对应序数的年份具有十分相似的变化趋势(如2013和2017年,2012和2016年)。这不仅证明本节拟合算法具有改进太阳赤纬角计算精度的优势,也为后面展开法的提出提供了思路。
|
Download:
|
| 图 1 2011—2018年太阳赤纬角拟合改进算法与传统算法误差对比曲线 Fig. 1 Comparison of error curves belween the fitting algorithm of the solar declination and the original ones(2011-2018) | |
为定量说明数值拟合法相比原算法(指Bourges算法等传统太阳赤纬角算法)的精度改进情况,表 3列出2018年太阳赤纬角计算的不同算法误差均方根、误差和方差、误差均值。结果表明,本文改进后太阳赤纬角算法的误差均方根可以控制在10-3级别,例如2018年误差均方根为0.006 65°,而传统算法的误差均方根多在10-1度级别,数值拟合法对太阳赤纬角的计算精度改进效果显著。
|
|
表 3 太阳赤纬角拟合改进算法与传统算法误差数据对比(2018年) Table 3 Comparison of errors between the fitting algorithm of declination and the original ones in 2018 |
在1.3节的研究过程中发现,太阳赤纬角的计算误差变化趋势具有周期性,不同周期内相对应年份误差曲线变化趋势具有很大相似性(如2017与2013年),同一周期内不同年份误差曲线变化趋势不同,尤其平年和闰年计日序数的区别会影响计算准确性。于是本文根据前文拟合法误差曲线反映的周期规律,以4年为周期,基于傅里叶展开法,提出一种误差更小的太阳赤纬角改进算法。这种算法充分考虑平年和闰年在计日序数方面存在差异,以4年总计日序数为基准修正积日因子β,利用傅里叶展开法求出每一项展开系数,不同年份所在周期的系数不同,太阳赤纬角可以表示为
| $ \begin{array}{l} {n_0} = 79.6764 + 0.2422(n - 1985) - \\ {\mathop{\rm int}} (n - 1985),\beta = \frac{{2{\rm{ \mathsf{ π} }}\left( {{d_n} - 1 - {n_0}} \right)}}{{365.2422}},\\ \delta = {a_0} + \sum\limits_{k = 1}^5 {{a_k}} \cos (k\beta ) + \sum\limits_{k = 1}^5 {{b_k}} \sin (k\beta ). \end{array} $ | (7) |
式中:n为该周期内第3年的年份数;dn为该周期内的总计日序数;ak, bk为展开系数。选取2015—2018年这一周期,给出式(7)所涉及的展开项系数,如表 4所示。
|
|
表 4 傅里叶展开法公式系数(2015—2018年) Table 4 Coefficients in Fourier expansions from 2015 to 2018 |
对于其他年份所在周期,根据具体年份调整β因子,再次使用展开法即可重新求出新的展开系数。选取传统算法中误差最小的Wang算法,结合天文年历和本文算法进行误差计算与对比。表 5具体给出本世纪4个周期内改进算法的误差均方根和原算法对比数据。结果显示,本文算法误差均方根可达到10-4级别,相比传统太阳赤纬角算法在误差均方根精度方面有2个数量级的提升,并且该方法比数值拟合法误差更低。展开法以4年为周期进行太阳赤纬角计算,更加符合太阳赤纬角误差变化规律,有利于减少平年与闰年计日序数差异对于太阳赤纬角计算的影响,同时也避免过于复杂的计算量,保持计算过程的简洁性。
|
|
表 5 太阳赤纬角展开算法与传统算法误差数据对比 Table 5 Comparison of errors between the expansion algorithm of declination and the original ones |
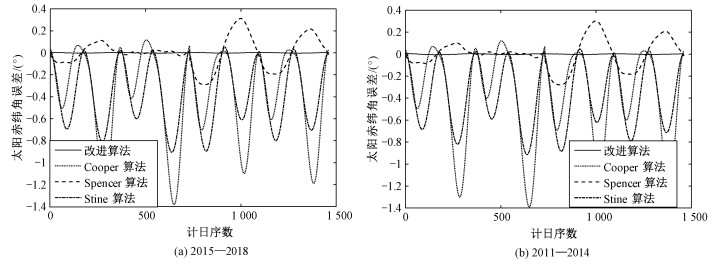
为直观体现计算精度的提升效果,图 2分别表示2015—2018年和2011—2014年的两个周期内,展开法与传统算法之间的误差对比曲线。图中实线代表本位提出的基于傅里叶展开法改进后的算法误差曲线,其他不同形式的虚线分别代表传统算法误差曲线。结果表明,改进算法误差曲线的波动范围明显小于传统算法,误差均值降低,而且两个周期内曲线的变化趋势相一致,符合本文基于展开法以4年为周期改进太阳赤纬角计算精度的设想。
|
Download:
|
| 图 2 太阳赤纬角展开算法与传统算法误差对比曲线 Fig. 2 Comparison of error curves between the expansion algorithm of declination and the original ones | |
除太阳赤纬角外,太阳时角是另一个决定太阳高度角计算的重要因素。前文已经介绍过其定义,其计算公式为
| $ \omega=\frac{\pi}{12}\left(t_{s}-12\right). $ | (8) |
式中:ts为真太阳时,h。这里介绍一下太阳日和太阳时的概念,太阳日表示日心连续2次通过同一个子午圈的时间间隔,一个平太阳日包括24个平太阳时。由于地球绕日公转的速度在不断变化,并且赤道与黄道为异面关系,一年中太阳日长短也存在差别[17]。真太阳时并不均匀,为计算方便,需要一个均匀的时间单位,平太阳这个假想的概念便被引进。平太阳以赤道为轨道运动,其运动周期与视太阳运动周期保持一致,运动速度则与视太阳运动的平均速度相等。基于平太阳时的系统为常用的时间系统,把平时转换为视时是太阳时角实时计算的重要工作,用时差eot (equation of time)表示视时与平时的差。时差的误差精度会影响太阳时角的精度,进而影响太阳高度角的计算。真太阳时ts与北京时间对应的平太阳时t以及时差eot的关系如下
| $ t_{s}=t+\operatorname{eot}+\frac{(\lambda-120)}{15}. $ | (9) |
式中:λ为所在地经度,东经为正。
下面针对不同时差算法进行误差计算和对比分析。
Wloof[5]提出的时差算法如下
| $ \begin{array}{*{20}{r}} {{\rm{eot}} = 0.258\cos \theta - 7.416\sin \theta - }\\ {3.648\cos (2\theta ) - 9.228\sin (2\theta ).} \end{array} $ | (10) |
式中:θ为日角,
Spencer[4]给出的时差算法如下
| $ \begin{array}{l} {\rm{eot}} = 229.18[0.000075 + 0.001868\cos \theta - \\ \;\;\;\;\;\;\;\;0.032077\sin \theta - 0.014615\cos (2\theta ) - \\ \;\;\;\;\;\;\;\;0.04089\sin (2\theta )]. \end{array} $ | (11) |
式中:
Whillier [9]提出时差算法如下
| $ {\rm{eot}} = 9.87\sin (2\theta ) - 7.53\cos \theta - 1.5\sin \theta . $ | (12) |
式中:
Lamm[8]算法考虑平年与闰年的区别,给出时差算法如下
| $ {\rm{eot}} = \sum\limits_{k = 0}^5 {\left( {{A_k}\cos \frac{{2{\rm{ \mathsf{ π} }}kN}}{{365.25}} + {B_k}\sin \frac{{2{\rm{ \mathsf{ π} }}kN}}{{365.25}}} \right)} . $ | (13) |
式中:N为一个周期中的计日序数,以闰年开始进行以4年为周期的循环;ak和bk为一个周期内不同年份所对应的系数,不同周期系数相同。
Yu[7]采用的时差算法如下
| $ \begin{aligned} \mathrm{eot}=& 0.0172+0.4281 \cos \theta-7.351 \sin \theta-\\ & 3.3495 \cos (2 \theta)-9.3619 \sin (2 \theta). \end{aligned} $ | (14) |
式中:
本文结合天文年历,以Matlab为工具,计算分析不同算法下时差的误差情况,在此给出图 3表示2018年不同太阳时角算法误差在一年内随计日序数变化情况。结果显示,Lamm算法精度最高,误差均值仅为0.002 ″,而且该方法计算过程并不复杂,所以在太阳时角计算时可以选取这种方法。

|
Download:
|
| 图 3 2018年不同时差算法误差曲线 Fig. 3 Error curves of different algorithms of error of time in 2018 | |
本节讨论太阳高度角的改进计算,传统算法采用地球球体模型,通过球面三角公式计算太阳高度角。本文考虑地球扁率带来的长短半径区别给太阳位置计算造成的误差,推导地球椭球模型中太阳高度角公式。
椭球模型中,假设地球长半轴半径为a,短半轴半径为b,则椭球存在扁率公式如下
| $ e=\frac{a-b}{a}. $ | (15) |
椭球模型上假设点B为太阳直射点,太阳赤纬角为δ,在椭球模型上选取一点A作为研究对象,ϕ为A点纬度,B点的直角坐标系坐标可以表示为B(acosδ, 0, bsinδ), 太阳直射方向表示为(acosδ, 0, bsinδ)。A点在椭球坐标系中可以表示为A(r, ϕ, ω), ω为太阳时角,则A点的直角坐标系坐标为A(acosϕcosω, acosϕsinω, bsinϕ), 则过A的法向方向为
| $ \begin{array}{*{20}{c}} {\cos \varphi = \frac{{\cos \phi \cos \omega \cos \delta + \sin \phi \sin \delta }}{{\sqrt {{a^2}{{\cos }^2}\delta + {b^2}{{\sin }^2}\delta } \sqrt {\frac{{{{\cos }^2}\delta }}{{{a^2}}} + \frac{{{{\sin }^2}\delta }}{{{b^2}}}} }}}\\ { = \frac{{\cos \varphi \cos \omega \cos \delta + \sin \varphi \sin \delta }}{{\sqrt {1 + \left[ {\frac{1}{{{{(1 - e)}^2}}} - 1} \right]{{\cos }^2}\delta {{\sin }^2}\varphi + \left[ {{{(1 - e)}^2} - 1} \right]{{\cos }^2}\varphi {{\sin }^2}\delta } }}.} \end{array} $ | (16) |
式中:δ为太阳赤纬角,ϕ为所在地纬度,ω为太阳时角, e为椭球扁率,公式(16)为椭球坐标系下太阳高度角余弦值的表达式。不难看出,当a与b相等时,椭球模型退化成球体模型,该式与球体模型下太阳高度角公式相一致[18]。
2.2 改进算法与传统算法误差对比前文已经验证以4年为周期计算太阳赤纬角更符合其误差变化规律,故本文对于太阳高度角的计算同样以4年为一周期,其中太阳赤纬角计算即选取前文提出的傅里叶展开法,太阳时角的时差计算选取Lamm算法,而太阳高度角改进公式选择本文提出的公式(16)。把本文基于椭球模型的太阳高度角改进算法与球体模型中几种传统算法的计算结果进行误差对比,结果表明,本文算法的误差均方根、均值、最大值均明显减小。为定量说明,以2011—2014年和2015—2018年两个周期为例,给出具体误差数据如表 6所示。本文太阳高度角算法误差均值达到10-4数量级,误差均方根达到10-3数量级,而表中基于球体模型的几种传统算法误差均方根和误差均值都在10-2~10-1数量级。
|
|
表 6 本文太阳高度角算法与传统算法误差比较 Table 6 Comparison of the errors between the solar elevation angle algorithm and the original ones |
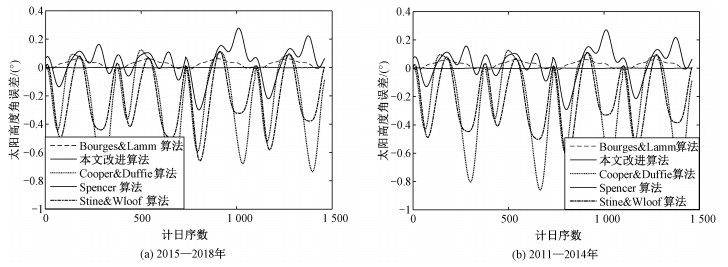
为更为直观地体现不同太阳高度角算法误差在一个周期内随着计日序数的变化情况,图 4给出不同算法在2011—2014年和2015—2018年两个周期的误差变化对比曲线。粗实曲线表示本文改进算法在这4年内随计日序数变化的情况,其他曲线代表各种传统算法在球体模型中的计算误差变化情况。结果表明,粗实曲线波动范围明显小于其他曲线,误差均值也明显低于传统算法,而且两张图中曲线体现出十分相似的变化规律。这不仅证明本文椭球模型下太阳高度角算法对于精度的改进提升效果明显,同时也再次说明以4年为周期的设想符合太阳位置计算规律。对于其他年份所在周期,可以根据所需求解的年份调整系数从而保持高计算精度,节省了复杂算法巨大的计算量。
|
Download:
|
| 图 4 本文太阳高度角算法与传统算法误差变化曲线 Fig. 4 Error curves of the solar elevation angle algorithm and the original ones | |
影响太阳高度角计算的另一个重要因素来自大气对于太阳光线的折射,尤其在低仰角条件下,大气折射所带来的蒙气差不可忽略。蒙气差是太阳光线经过大气层的不同介质时,由于不同介质折射率不同导致的光线路径改变的现象[19]。由于蒙气差的存在,观测到的太阳高度和实际太阳位置存在差别。
| $ \Delta \zeta = \int_1^{{n_0}} {\frac{{\tan \zeta }}{n}} {\rm{d}}n,nr\sin \zeta = {n_0}{r_0}\sin {\zeta _0} = {\rm{const}}. $ | (17) |
式中:n表示大气传输路径上某处大气位相折射指数,ζ表示该点地心方向半径和平面电磁波方向的夹角,r表示几何地心距;n0、ζ0和r0分别是观测点相应的参数。张捍卫等[23]在此基础上进一步推导出蒙气差展开式
| $ \begin{array}{l} y = \frac{{{n_0}{r_0}}}{{nr}},\\ \tan \zeta = \frac{{y\tan {\zeta _0}}}{{\sqrt {1 + \left( {1 - {y^2}} \right){{\tan }^2}{\zeta _0}} }},\\ E(k) = \frac{{(2k - 1)!!}}{{(2k)!!}}\int_1^{{n_0}} {\frac{1}{n}} y{\left( {1 - {y^2}} \right)^k}{\rm{d}}n,\\ \Delta \zeta = \sum\limits_{k = 0}^\infty {{{( - 1)}^k}} \frac{{{{\tan }^{2k + 1}}{\zeta _0}}}{{{{\left( {1 + \chi {{\tan }^2}{\zeta _0}} \right)}^{\frac{{2k + 1}}{2}}}}}\\ \left[ {E\left( k \right) + \sum\limits_{j = 1}^k {\frac{{{{\left( { - 1} \right)}^j}k!}}{{\left( {k - j} \right)!}}{\chi ^j}E\left( {k - j} \right)} } \right]. \end{array} $ | (18) |
式中,Δζ以级数和的形式表示蒙气差。但是此算法仅适用于仰角大于9°的情况,而且χ的取值并未确定给出,这会对级数展开的收敛性产生影响。蒙气差的计算分为不考虑温度气压因素影响的常差部分,以及受这些因素影响的附加部分。文献[24-28]分别提出5种关于常差的算法,在此称为原算法1~5,上述算法给出了确切的计算公式,但在低仰角下,这些传统算法仍然无法避免过大误差。
文献[24]提出一种粗略的蒙气差常差算法如下,称为原算法1:
| $ {R_0} = 60.2\tan z. $ | (19) |
式中:z表示天顶角,也就是仰角的余角;R0表示蒙气差常差。
文献[25]提出另一种传统算法近似表达如下,称为原算法2。
| $ {R_0} = \frac{{1819.08 + 194.89\alpha + 1.47{\alpha ^2} - 0.042{\alpha ^3}}}{{1 + 0.41\alpha + 0.067{\alpha ^2} + 0.000085{\alpha ^3}}}. $ | (20) |
式中:α表示仰角。
文献[26]给出的传统算法如下,称为原算法3。
| $ {R_0} = \frac{{1.02}}{{\tan \left[ {\left( {\alpha + \frac{{10.3}}{{\alpha + 5.11}}} \right)\pi /180} \right]}}. $ | (21) |
文献[27]提出传统算法可近似表达如下,在文中称为原算法4。
| $ \begin{aligned} R_{0}=& 60.097 \tan z+0.0109 \tan ^{2} z-\\ & 0.073 \tan ^{3} z+0.002 \tan ^{4} z. \end{aligned} $ | (22) |
式中:z表示天顶角。
文献[28]给出的传统算法近似表达如下,称为原算法5。
| $ R_{0}=60.103 \tan z-0.066 \tan ^{3} z-0.00015 \tan ^{5} z. $ | (23) |
原算法1~5均为计算蒙气差常差的传统算法,针对较高仰角范围的计算具有一定准确性,在低仰角条件下误差较大。本文对低仰角区间分段,提出0°~30°仰角下更为精确的蒙气差改进公式。在仰角0°~14°区间,太阳光线受到的大气折射最为明显,这部分本文采用傅里叶展开法进行蒙气差常差改进计算,数据样本来自2018年天文年历[29],展开结果如下
| $ R_{0}=a_{0}+\sum\limits_{k=1}^{5} a_{k} \cos (k \psi \times w)+\sum\limits_{k=1}^{5} b_{k} \sin (k \psi \times w). $ | (24) |
式中:R0为蒙气差常差,(″);ψ为仰角余切值;展开式每一项系数如表 7所示。
|
|
表 7 0°~14°仰角下展开系数 Table 7 Expansion coefficients at elevation angles of 0°-14° |
以Matlab为工具,计算并对比本文算法与几种传统算法之间的误差,不同算法误差均方根如表 8。结果表明,本文算法在0°~14°俯仰角误差均方根为0.113 6″,而传统算法由于是针对较高仰角范围提出,无法避免低仰角下的巨大误差,在0°~14°区间的准确性远远不如改进算法。
|
|
表 8 改进算法与传统算法误差均方根比较(0°~14°仰角) Table 8 Comparison of the root mean square error between the expansion algorithm and the original ones (0°-14° elevation) |
在14°~30°区间,本文采用数值拟合法给出常差计算公式,同样以天文年历记录值为样本数据,拟合因子为仰角余切值,这段的蒙气差常差改进算法可以表示
| $ R_{0}=\sum\limits_{k=0}^{7} a_{k} \cot ^{k}(\alpha). $ | (25) |
式中:R0为蒙气差常差,(″);α为仰角。14°~30°仰角区间的相关系数如表 9所示。
|
|
表 9 14°~30°仰角下拟合法蒙气差常差系数 Table 9 Fitting coefficients of atmosphere refraction at elevation angles of 14°-30° |
和14°~30°区间类似,30°~45°仰角区间同样可以通过拟合法进行计算,相关系数需要调整,在此不详细展开。在表 10中,本文给出上述两个仰角区间的不同算法误差均方根、均值等数据对比情况。结果显示,在仰角14°~45°区间,本文算法误差均值精度达到10-13量级,原算法误差均值至少10-4量级。本文算法相比传统算法误差明显减小,蒙气差常差计算精度得以改进。
|
|
表 10 改进算法与传统算法误差均方根比较(14°~45°俯仰角) Table 10 Comparison of the root mean square error between this algorithm and the original ones (14°-45° elevation)(″) |
为了直观体现本文针对14°~30°仰角下本文蒙气差常差计算的准确性,图 5给出本文算法分别与原算法的误差对比曲线,图 5(a)表示本文拟合算法在14°~30°仰角区间的误差变化曲线,图 5(b)~5(d)分别表示本文算法与传统算法的误差对比。其中,原算法1~3分别代表文献[24-26]中提到的算法。结果显示,本文拟合算法对于蒙气差常差的计算精度明显提升,图中体现的变化趋势与表 10的计算结果相一致。

|
Download:
|
| 图 5 本文拟合算法与传统算法误差比较 Fig. 5 Error comparison between the fitting algorithms and the original ones | |
除仰角外,蒙气差主要还受到温度和气压的影响,在此引入系数A和B,A为温度系数,公式如下
| $ A=\frac{-0.00383(T-273.15)}{1+0.00363(T-273.15)}. $ | (26) |
式中:T为温度,K。
B为气压系数,公式如下
| $ B=\frac{P}{101324.72}-1. $ | (27) |
式中:P为气压,Pa。
综合上述公式,蒙气差可以表示为
| $ R=R_{0}(1+A+B). $ | (28) |
式中:R0为蒙气差常差,(″); R为考虑温度气压影响的蒙气差,s。
式(28)适用于仰角大于45°时蒙气差的计算,对于仰角小于45°的情况,太阳光线受大气折射的影响,还需要一个附加值μ乘以温度系数,附加值与仰角相关。在文献[27-28]中,给出两种附加系数的算法,但经过计算分析,两种方法误差明显。本文使用数值拟合法给出附加值的公式如下
| $ \mu=\sum\limits_{k=0}^{5} a_{k} \cot ^{k}(\alpha). $ | (29) |
式中:μ为蒙气差附加系数,(″);α为仰角。具体系数如表 11所示。
|
|
表 11 蒙气差附加值拟合系数 Table 11 Fitting coefficients for the additional value of the atmosphere refraction |
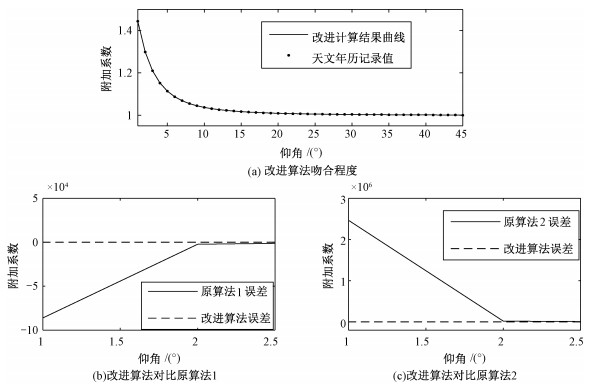
本文以天文年历记录的附加值为依据,图 6给出不同算法之间的误差对比。图 6(a)显示本文附加值改进算法与天文年历记录值的吻合程度,图 6(b)和图 6(c)分别给出本文算法与传统算法的误差对比,图中用原算法1~2分别代表文献[27-28]提出的算法。结果表明,本文对于附加值的计算误差均值和波动性明显小于两种传统算法,此改进公式可以用来计算低仰角下的附加系数。
|
Download:
|
| 图 6 本文附加值算法与传统算法误差比较 Fig. 6 Error comparison between the algorithm of the additional value and the original ones | |
本文以太阳位置计算为主要研究对象,针对传统简单算法误差较大而复杂算法不利于工程项目应用的不足,本文对于太阳位置计算提出改进方法。首先由于传统太阳赤纬角算法针对不同年份采用相同系数的公式,对不同年份之间的差异考虑不足,本文使用数值拟合法提出可以根据年份调整系数的改进公式,结果表明,拟合法改进太阳赤纬角算法的误差均方根可以控制在10-3级别,例如2018年误差均方根为0.006 5°,Bourges算法误差均方根为0.011 18°,Cooper算法误差均方根为0.546 11°,Spencer算法误差均方根为0.149 05°,Stine算法误差均方根为0.466 32°,Yu算法误差均方根为0.194 13°。结果表明,数值拟合法对太阳赤纬角的计算精度改进效果显著。随后根据误差曲线体现出的周期性变化规律,采用傅里叶展开法提出以4年为周期的太阳赤纬角改进算法,2011—2014年周期内太阳赤纬角改进算法误差均方根为(8.906×10-4)°,传统算法中误差最小的Bourges算法误差均方根为0.01097°,2015—2018年周期内太阳赤纬角改进算法误差均方根为(5.521×10-4)°,Bourges算法误差均方根为0.011 28°。结果表明,展开法改进算法的计算精度至少提高两个数量级。然后针对地球球体模型在传统太阳位置计算中过于理想化的不足,本文基于地球椭球模型推导出太阳高度角的改进公式,根据太阳赤纬角误差变化的周期性规律,太阳赤纬角算法应用本文所提出的展开法,一个周期内太阳高度角计算的误差均方根可以达到10-3级别,太阳高度角的改进算法同样可根据不同年份可以调整公式系数,相比传统简单算法明显改进计算精度,并且省去了传统复杂算法的巨大计算量。蒙气差的存在导致观测太阳位置和计算太阳位置之间存在误差,而传统蒙气差算法在低仰角下误差过大,本文针对仰角低于30 °的情况,对于仰角分段并分别利用展开法和拟合法给出更为精确的改进公式。相比传统蒙气差算法,蒙气差常差改进算法的误差均值、误差均方根都明显降低,其中0°~14°仰角下的误差均方根降低到0.113 6″,14°~30°仰角下的误差均方根降低到(4.113 4×10-3)″,30°~45°仰角下的误差均方根降低到(3.923 5×10-3)″,传统算法针对仰角范围比较笼统,主要适用于较高仰角下蒙气差的计算,低仰角下无法避免过大误差,对于附加系数的改进公式同样比原算法更为准确。蒙气差计算精度的提升可以间接帮助实现太阳位置计算的改进。
5 总结与展望人类社会如何应对全球变化、实现可持续发展,是当前人类社会发展面临的重大挑战[30]。提高对于太阳能等可再生能源的利用率有利于人类社会长久发展。本文基于地球椭球模型提出一系列太阳位置算法,兼顾简单算法的高效和复杂算法的准确性。未来还会进一步针对太阳时角的改进计算进行深入研究,从而进一步改进太阳位置计算的精确度。相关研究对于提升太阳追踪技术具有实用价值。另外,全球遥感技术快速发展,中国在高分辨率遥感领域的技术也在不断发展,空间对地观测数据获取能力不断提升,空间信息保障能力显著提升[31-32]。准确高效的太阳位置计算对于在微光条件下的遥感辐射定标等工程项目具有积极意义。
| [1] |
路博.光伏系统中的高精度太阳跟踪方法研究[D].河南新乡: 河南师范大学, 2012.
|
| [2] |
卢国杰.基于GPS的太阳跟踪控制系统研究[D].北京: 华北电力大学, 2013.
|
| [3] |
Cooper P I. The absorption of radiation in solar stills[J]. Solar Energy, 1969, 12(3): 333-346. |
| [4] |
Spencer J W. Fourier series representation of the position of the sun[J]. Search, 1971, 2(5): 172. |
| [5] |
Stine W B. Solar energy fundamentals and design with computer applications[M]. New York: Jone Wiley & Sons, 1985: 38-69.
|
| [6] |
Bourges B. Improvement in solar declination computation[J]. Solar Energy, 1985, 35(4): 367-369. |
| [7] |
Yu H. Study on the formula of the solar declination and time difference in meteorology[J]. Meteorological, Hydrological and Marine Instrument, 2006, 3(4): 50-53. |
| [8] |
Lamm L O. A new analytic expression for the equation of time[J]. Solar Energy, 1981, 26(5): 465. |
| [9] |
Duffle J A, Beckman W A. Solar engineering of thermal processes[M]. New York: Jone Wiley & Sons Inc, 1980: 8-28.
|
| [10] |
Reda I, Andreas A. Solar position algorithm for solar radiation applications[J]. Solar Energy, 2004, 76(5): 577-589. |
| [11] |
Grena R. An algorithm for the computation of the Solar position[J]. Solar Energy, 2008, 82(5): 462-470. |
| [12] |
Blanco M, Alarcon D C, Lopea M T, et al. Computing the solar vector[J]. Solar Energy, 2001, 70(5): 431-441. |
| [13] |
Sproul A B. Derivation of the solar geometric relationships using vector analysis[J]. Renew Energy, 2007, 32(7): 1187-1205. DOI:10.1016/j.renene.2006.05.001 |
| [14] |
Xue B S, Han D Y. Simulation of the sun position and geomagnetic parameters effect in pigeon homing navigation[J]. Navigation and control, 2017, 16(2): 25-29. |
| [15] |
Wang G A, Mi H T, Deng T H, et al. Calculation of the change range of the sun high angle and the azimuth of sunrise and sunset in one year[J]. Meteorological and Environmental Sciences, 2007, 30(9): 161-164. |
| [16] |
Wang B Z, Liu G S. Improvement in the astronomical parameters computation for solar radiation observation[J]. Acta Energiae Solaris Sinica, 1991, 12(1): 28-32. |
| [17] |
Wang C L. Calculating the parameters that relate to the sun in calculation model of the ionosphere electron concentration[J]. Journal of CAEIT, 2013, 1(8): 86-90. |
| [18] |
Long X. The design of automatic sun tracking system[D]. Changsha: Hunan University, 2013.
|
| [19] |
Men T, Shi J X, Xu R, et al. Correction method of atmospheric refraction based on the low elevation infrared measurement[J]. Infrared and Laser Engineering, 2016, 45(1): 0117004. |
| [20] |
Saastamoinen J. Contributions to the theory of atmospheric refraction(Part I)[J]. Bulletin Geodesique, 1972, 46(3): 279-298. |
| [21] |
Saastamoinen J. Introduction to practical computation of astronomical refraction[J]. Bulletin Geodrsique, 1972, 46(4): 383-397. |
| [22] |
Saastamoinen J. Contributions to the theory of atmospheric refraction (Part Ⅱ)[J]. Bulletin Greodesique (1946-1975), 1973, 107(1): 13-34. |
| [23] |
张捍卫, 雷伟伟, 丁安民. 低高度角处的蒙气差级数展开式[J]. 天文学报, 2013, 54(6): 562-568. DOI:10.3969/j.issn.0001-5245.2013.06.006 |
| [24] |
张同双, 钟德安, 李晓勇, 等. 基于递推最小二乘算法的惯导姿态误差动态标定方法[J]. 电讯技术, 2011, 51(8): 11-15. DOI:10.3969/j.issn.1001-893x.2011.08.003 |
| [25] |
Zhang F, Zhang L J, Qiu B Z. A rational function approximation method to calculate atmosphere refraction as the solar in low angle[J]. Acta Energiae Solaris Sinica, 2015, 36(9): 2189-2195. |
| [26] |
Saemundsson K. Atmospheric refraction[J]. Sky and Telescope, 1986, 72(1): 70. |
| [27] |
Guo J M, Zhao J Y, He X, et al. Calibration of installation angle for high accuracy shipboard star sensor[J]. Optics and Precision Engineering, 2016, 24(3): 609-615. DOI:10.3788/OPE. |
| [28] |
Mao Y X, Zhang T S, Zhu W K, et al. A real-time atmospheric refraction correction method for measurement data of ship-borne star sensors[J]. Journal of Spacecraft TT&C Technology, 2012, 31(3): 50-53. |
| [29] |
中国科学院紫金山天文台. 2018年中国天文年历[M]. 北京: 科学出版社, 2017: 594-59.
|
| [30] |
毛萍, 黄东晓, 王芋华, 等. 全球变化领域研究现状与趋势的大数据分析[J]. 中国科学院大学学报, 2017, 34(4): 441-451. |
| [31] |
江威, 何国金, 彭燕, 等. 夜光遥感在"一带一路"战略中的应用潜力展望[J]. 中国科学院大学学报, 2017, 34(3): 296-303. |
| [32] |
袁益琴, 何国金, 王桂周, 等. 背景差分与帧间差分相融合的遥感卫星视频运动车辆检测方法[J]. 中国科学院大学学报, 2018, 35(1): 50-58. |
 2019, Vol. 36
2019, Vol. 36 



