银河系晕是探究银河系的形成和演化的关键。现在宇宙学理论认为:银河系晕星由于成分不同有着不同的形成机制。主要分为两大类:第一类是“原位(in-situ)”晕星,这些晕星主要通过外部气体物质向银河系中心区域塌缩而形成[1-3], 不过其中也有的星可能由于星系加热[4],双星系统的超新星爆发[5],或者是其他机制,从银河系盘中被“剔除(kick-out)”出来。另一类是并合晕星,主要通过并合小星系而形成,例如矮球状(dSph)星系[6-8]。
尽管已经发现了一些被厚盘“剔除”出来的高速富金属晕星[9],但是到目前为止已知的晕星样本大多为贫金属星,其金属丰度大约只有太阳的1/10[10-12]。Carollo等[11-12]和Beers等[13]发现可以将晕分为内晕(inner-halo)和外晕(outer-halo)两部分。这两部分有不同的化学丰度分布和运动学性质。他们认为内晕主要分布在距离银心10~15kpc以内的区域,平均旋转速度
本文主要用LAMOST数据研究银河系晕星的偏心率性质。
1 数据 1.1 观测数据郭守敬望远镜(LAMOST,大天区面积多目标光纤光谱天文望远镜)位于中国科学院国家天文台兴隆观测站,是一架有效口径约4m,视场约5°的“王-苏反射施密特望远镜”。LAMOST有4000根光纤,可以同时获得4000个天体的光谱[18-20],因此具有很高的光谱获取率。巡天的第4批数据已经释放,其中恒星光谱有6898298条,包含有计算出的恒星大气参数以及视向速度(line-of-sight velocity)。包括恒星光谱型、金属丰度[Fe/H]、表面重力log g在内的大气参数通过Ulyss计算[21],而视向速度是交叉匹配恒星光谱和Elodie模版[22]得出的。反银心方向巡天项目LSS-GAC的增值星表[23]又加入距离,[a/Fe]等关键要素。
本文采用LAMOST第4批释放数据中的恒星大气参数和视向速度,结合LSS-GAC增值星表中的距离,恒星的自行则是来自PPMXL自行星表[24]。接下来,通过限制log g < 3.5,样本星光谱g波段的信噪比S/N大于15,得到巨星样本462000颗。
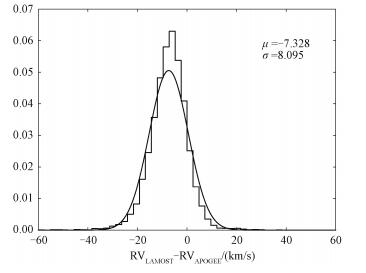
Jing等[25]对比LAMOST与SDSS-SSPP得出的视向速度,得到一个-6.76km/s的系统偏差。我们则将巨星样本与平均信噪比大于15的SDSS DR14 APOGEE样本匹配得到17203颗共同星,结果显示在图 1中。由图可知,视向速度的系统偏差为-7.328km/s, 弥散为8.095km/s。这个系统偏差的原因尚不清楚,在本文中,为了与其他巡天数据相符,在LAMOST的视向速度数据上加上7.328km/s。
|
Download:
|
| 图 1 LAMOST和APOGEE的视向速度偏移 Fig. 1 The offsets of the radial velocities between the LAMOST pipeline and the APOGEE | |
通过恒星的距离、自行和视向速度,计算出恒星相对于太阳的U, V, W空间速度分量。采用太阳相对于局域静止坐标系(local standard rest, LSR)的速度(U, V, W)=(9.58, 10.52, 7.01)km/s[26],转换恒星的速度到相对于LSR的速度。采用VLSR=220km/s和太阳距银心距离R⊙=8kpc得出恒星以银心为中心的柱坐标系和球坐标系中的速度分量,同时求得恒星的垂直距离Z和距离银心的水平距离R。
为了得到晕星的样本,首先限制|z| > 5kpc,距离的相对误差小于0.3,自行误差小于10mas/a,以及柱坐标三维速度(|VR, |
|
Download:
|
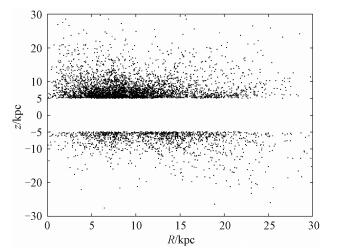
| 图 2 巨星样本在|z|>5kpc范围内Z-R面的空间分布 Fig. 2 Spatial distribution in the Z-R plane of the giant stars in the |z|>5kpc range | |
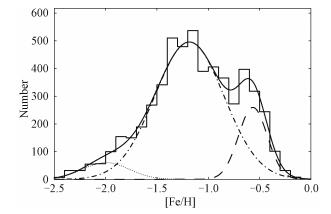
然后画出晕星样本的金属丰度分布图,通过贝叶斯参数(BIC)[27]值越小拟合程度最优的原则发现用三高斯模型拟合效果最好,如图 3所示,根据Carollo等[11-12]的结果,我们推测图中从贫金属端到富金属端点线、点画线、虚线的部分分别表示外晕星、内晕星、厚盘星,对应的峰值为[Fe/H]~-2.0, -1.2, -0.6,所占比例为6%,77%,17%。为尽可能地排除盘星对结果的影响,选择[Fe/H] < -0.8作为最终的晕星样本,总共4344颗。
|
Download:
|
| 图 3 |z|>5kpc的巨星金属丰度分布 Fig. 3 Metallicity distribution functions of giant stars in the |z| >5kpc range | |
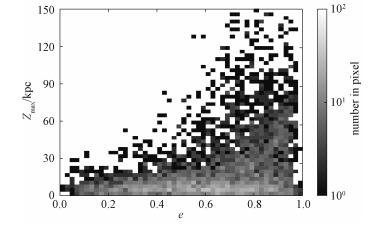
接下来利用这一样本星研究银河系晕星的偏心率性质。首先计算恒星的轨道偏心率,采用的银河系的引力势来自Xue等[28],包括球状Hernquist (1990)核球、指数银盘和NFW暗物质晕[29]。恒星轨道偏心率定义为
|
Download:
|
| 图 4 样本星的最大垂直距离Zmax和偏心率e分布图 Fig. 4 The maximum vertical height Zmax vs. orbital eccentricities for the sample stars | |
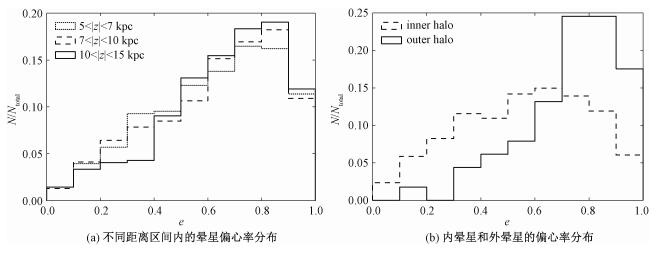
然后研究偏心率和垂直距离之间的关系,图 5(a)给出晕星在不同距离的偏心率分布图,其中点线、虚线、实线分别表示5 < |z| < 7kpc, 7 < |z| < 10kpc, 10 < |z| < 15kpc距离范围内晕星的偏心率分布直方图。从图中可以发现,随着距离的增大,偏心率的峰值略微增大,维持在0.8左右,但峰值处所占比例随垂直距离增大而增大,所以垂直距离越远,恒星偏心率分布越集中(集中在e~0.8)。Sesar等[30]发现距离银心5~35kpc内晕星的轴比q≡c/a=0.70±0.01, 并没有随着距离的改变而改变,Deason等[31]的结果表明这个稳定的轴比为q~0.6,根据轴比和偏心率的关系
|
Download:
|
| 图 5 晕星偏心率分布直方图 Fig. 5 Histogram of eccentricity distributions | |
由图 3金属丰度分布方程(MDFs)的高斯拟合模型可以区分晕的不同成分:内晕和外晕,图中内晕的峰值在[Fe/H]~-1.2处,标准差的值约为0.3,我们取-1.5 < [Fe/H] < -0.9作为内晕星的样本。由于图中外晕的峰值在[Fe/H]~-2.0处,标准差约等于0.2,而在这个标准差范围内外晕星和内晕星存在很大的重叠,所以这里将[Fe/H] < -1.9的星作为外晕星样本。除金属丰度外,Carollo等[12]还给出根据最大垂直距离Zmax区分内外晕的方法,即在Zmax < 15kpc的范围内,内晕占主导,在Zmax>20kpc的区域外晕占主导。所以我们的内晕星样本的限制条件为-1.5 < [Fe/H] <-0.9和Zmax < 15kpc,而外晕的限制条件为-2.5 < [Fe/H] < -1.9和Zmax>20kpc,内外晕样本星的数量分别为1142和114。图 5(b)展示内晕星和外晕星偏心率的分布,其中虚线表示内晕星,实线表示外晕星。从图中可以看到,从内晕到外晕,偏心率峰值发生明显的偏移,从0.65增大到0.8, 且外晕星的偏心率普遍大于0.6,而内晕星偏心率则分布较弥散。
根据以上分析可以推断,在垂直距离5 < |z| < 15kpc的范围内,样本星的偏心率在3个不同距离分区峰值均为0.8左右,与垂直距离分布无关,但随垂直距离增大,偏心率在0.8左右的样本星占比越大。此外,通过研究发现,在垂直距离5 < |z| < 25kpc的范围内,内晕星偏心率分布较弥散(从0.2~0.8几乎都有),峰值位于0.65左右;外晕星偏心率基本分布在e>0.6的区域,峰值在0.8左右。
3 总结基于LAMOST DR4的数据并结合反银心星表LSS-GAC,通过恒星的空间分布和化学丰度分布筛选出晕星样本并进行偏心率分布研究。具体地,首先通过空间分布|z|>5kpc筛选出可能的晕星,然后将所得的样本通过各成分金属丰度分布的不同进一步剔除盘星([Fe/H] < -0.8),最终得出所需的晕星样本。接下来利用这些候选星研究晕星偏心率的性质,经过分析发现:在距离银盘5~15kpc的范围内,晕星偏心率的峰值稳定在0.8左右,随着垂直距离的增大,峰值附近晕星所占比越大。在距离银盘5 ~25kpc的范围内,内晕星和外晕星在偏心率上的分布有明显差异,内晕星偏心率分布的峰值约为0.65,且分布弥散。而外晕星的偏心率大多集中在e>0.6的区域,峰值约为0.8。由此可见,内外晕偏心率分布不同。这些不同的运动学特征可能反映内外晕不同的特征,而这些特征也许预示着内外晕的形成机制不同。这有待于将来更精确的大样本光谱数据得到进一步验证。
| [1] |
Zolotov A, Willman B, Brooks A, et al. The dual origin of stellar halos. Ⅱ. Chemical abundances as tracers of formation history[J]. ApJ, 2010, 721(1): 738-743. DOI:10.1088/0004-637X/721/1/738 |
| [2] |
Font A S, Mccarthy I G, Crain R A, et al. Cosmological simulations of the formation of the stellar haloes around disc galaxies[J]. MNRAS, 2011, 416(4): 2802-2820. DOI:10.1111/j.1365-2966.2011.19227.x |
| [3] |
Cooper A P, Parry O H, Lowing B, et al. Formation of in situ stellar haloes in Milky Way-mass galaxies[J]. MNRAS, 2015, 454(3): 3185-3199. DOI:10.1093/mnras/stv2057 |
| [4] |
Purcell C W, Bullock J S, Kazantzidis S. Heated disc stars in the stellar halo[J]. ApJ, 2010, 404(4): 1711-1718. |
| [5] |
Bromley B C, Kenyon S J, Brown W R, et al. Runaway stars, hypervelocity stars, and radial velocity surveys[J]. ApJ, 2009, 706(2): 925-740. DOI:10.1088/0004-637X/706/2/925 |
| [6] |
Sales L V, Navarro J F, Abadi M G, et al. Satellites of simulated galaxies:survival, merging and their relationto the dark and stellar haloes[J]. MNRAS, 2007, 379(4): 1464-1474. DOI:10.1111/j.1365-2966.2007.12024.x |
| [7] |
Diemand J, Kuhlen M, Madau P, et al. Clumps and streams in the local dark matter distributio[J]. Nature, 2008, 454(7205): 735-738. DOI:10.1038/nature07153 |
| [8] |
Klypin A A, Trujillo-Gomez S, Primack J. Dark matter halos in the standard cosmological model:results from the bolshoi simulation[J]. ApJ, 2011, 740(2): 102-119. DOI:10.1088/0004-637X/740/2/102 |
| [9] |
Hawkins K, Kordopatis G, Gilmore G, et al. Characterizing the high-velocity stars of RAVE:the discovery of a metal-rich halo star born in the Galactic disc[J]. MNRAS, 2015, 447(2): 2046-2058. DOI:10.1093/mnras/stu2574 |
| [10] |
Chiba M, Beers T C. Kinematics of metal-poor stars in the galaxy. Ⅲ. Formation of the stellar halo and thick disk as revealed from a large sample of nonkinematically selected stars[J]. AJ, 2000, 119(6): 2843-2865. DOI:10.1086/301409 |
| [11] |
Carollo D, Beers T C, Lee Y S, et al. Two stellar components in the halo of the Milky Way[J]. Nature, 2007, 450(7172): 1020-1025. DOI:10.1038/nature06460 |
| [12] |
Carollo D, Beers T C, Chiba M, et al. Structure and kinematics of the stellar halos and thick disks of the Milky Way based on calibration stars from sloan digital sky survey DR7[J]. ApJ, 2010, 712(1): 692-727. DOI:10.1088/0004-637X/712/1/692 |
| [13] |
Beers T C, Carollo D, Ivezić Ž, et al. The case for the dual halo of the milky way[J]. ApJ, 2012, 746(1): 34-57. DOI:10.1088/0004-637X/746/1/34 |
| [14] |
An D, Beers T C, Santucci R M, et al. The fractions of inner-and outer-halo stars in the local volume[J]. ApJ, 2015, 813(2): L28-L34. DOI:10.1088/2041-8205/813/2/L28 |
| [15] |
Newberg H J, Yanny B, Rockosi C, et al. The ghost of Sagittarius and Lumps in the halo of the Milky Way[J]. ApJ, 2002, 569(1): 245-274. DOI:10.1086/apj.2002.569.issue-1 |
| [16] |
Deason A J, Belokurov V, Weisz D R. The progenitors of the milky Way stellar halo:big bricks favoured over little bricks[J]. MNRAS, 2015, 448(1): L77-L81. DOI:10.1093/mnrasl/slv001 |
| [17] |
Helmi A, Veljanoski J, Breddels M A, et al. A box full of chocolates:the rich structure of the nearby stellar halo revealed by Gaia and RAVE[J]. A&A, 2017, 598: A58-A76. |
| [18] |
Cui X Q, Zhao Y H, Chu Y Q, et al. The large sky area multi-object fiber spectroscopic telescope (LAMOST)[J]. RAA, 2012, 12(9): 1197-1242. |
| [19] |
Deng L C, Newberg H J, Liu C, et al. LAMOST experiment for galactic understanding and exploration (LEGUE):the survey's science plan[J]. RAA, 2012, 12(7): 735-754. |
| [20] |
Zhao G, Zhao Y H, Chu Y Q, et al. LAMOST spectral survey:an overview[J]. RAA, 2012, 12(7): 723-734. |
| [21] |
Wu Y, Luo A L, Li H N, et al. Automatic determination of stellar atmospheric parameters and construction of stellar spectral templates of the Guoshoujing Telescope (LAMOST)[J]. RAA, 2011, 11(8): 924-946. |
| [22] |
Moultaka J, Ilovaisky S A, Prugniel P, et al. The ELODIE archive[J]. PASP, 2004, 116(821): 693-698. DOI:10.1086/pasp.2004.116.issue-821 |
| [23] |
Xiang M S, Liu X W, Yuan H B, et al. LAMOST spectroscopic survey of the galactic anticentre (LSS-GAC):the second release of value-added catalogues[J]. MNRAS, 2017, 467(2): 1890-1914. |
| [24] |
Roeser S, Demleitner M, Schilbach E. The PPMXL catalog of positions and proper motions on the ICRS. Combining USNO-B1.0 and the two micron all sky survey (2MASS)[J]. AJ, 2010, 139(6): 2440-2447. DOI:10.1088/0004-6256/139/6/2440 |
| [25] |
Jing Y J, Du C H, Gu J Y, et al. Kinematics of the Galactic disc from a LAMOST dwarf sample[J]. MNRAS, 2016, 463(3): 3390-3397. DOI:10.1093/mnras/stw2230 |
| [26] |
Tian H J, Liu C, Carlin J L, et al. The stellar kinematics in the solar neighborhood from LAMOST data[J]. ApJ, 809(2): 145-162. DOI:10.1088/0004-637X/809/2/145 |
| [27] |
Ivezić Ž, Connolly A J, VanderPlas J T, et al. Statistics, data mining, and machine learning in astronomy[M]. Princeton: Princeton University Press, 2014: 190-191.
|
| [28] |
Xue X X, Rix H W, Zhao G, et al. The Milky Way's circular velocity curve to 60kpc and an estimate of the dark matter halo mass from the kinematics of~2400 SDSS blue horizontal-branch stars[J]. ApJ, 2008, 684(2): 1143-1558. DOI:10.1086/529169 |
| [29] |
Navarro J F, Frenk C S, White S D M. The structure of cold dark matter halos[J]. ApJ, 1996, 462: 563-575. DOI:10.1086/177173 |
| [30] |
Sesar B, Jurić M, I vezić Ž. The shape and profile of the Milky Way halo as seen by the Canada-France-Hawaii telescope legacy survey[J]. ApJ, 2011, 731(1): 4-17. DOI:10.1088/0004-637X/731/1/4 |
| [31] |
Deason A J, Belekurov V, Evans N W, et al. The Milky Way stellar halo out to 40kpc:squashed, broken but smooth[J]. MNRAS, 2011, 416(4): 2903-2915. DOI:10.1111/j.1365-2966.2011.19237.x |
 2019, Vol. 36
2019, Vol. 36 


