Classification is an important type of supervised learning problems for information extraction, which has attracted widespread attention among the machine learning and statistics communities. For example, assigning a given email into "spam" or "non-spam" class and optical character recognition task are two typical examples of statistical classification problems[1-2].
1 Statistical classificationFor a supervised classification problem with k classes, the training set consists of n samples {(xi, yi), i = 1, …, n}, which are independently and identically drawn from an unknown probability distribution P(X, Y). Here, the input xi denotes a p-dimensional covariates vector, and
A classifier is a rule based on the training data, so that by utilizing such a rule, one can assign a class label for a new observation. More specifically, the classifier
There are many different kinds of classifiers, which follow different criteria. Naive Bayes method follows the maximum a posterior decision rule. Fisher linear discriminant analysis is designed under some fundamental assumptions, i.e., the normally distributed classes. Based on the concept of entropy from information theory, decision tree learning is devised for classification. Neighbour-based learning is another type of classification based on instances, and it takes the local instances' similarity into consideration. Artificial neural networks are inspired by the biological neural networks. For more details, one can see Refs.[3-5]. In this article, we focus on the margin-based classifiers, which have drawn a great attention in the statistical machine learning community.
The rest of this article is organized as follows. In section 2, we briefly review some existing traditional classification methods, including binary and multicategory problems. We present a novel angle-based framework in section 3, which is more computationally efficient. We also show some new developments to handle multicategory problems under some complicated settings. In section 4, several theoretical results about Fisher consistency are summarized. Some discussions and suggestions are given in section 5.
2 Traditional methodsWe first give a brief review on regularization framework for binary classification in section 2.1, the extension for multicategory cases is then presented in section 2.2.
2.1 Binary classificationWhen k = 2, it is a typical binary example. Assume the class label is encoded as
| $ \min\limits _{f \in \mathscr{F}} \frac{1}{n} \sum\limits_{i=1}^{n} l\left(y_{i} f\left(\boldsymbol{x}_{i}\right)\right)+\lambda J(f), $ | (1) |
where
The commonly used binary convex loss functions are listed as follows.
·hinge loss[7-8]: l(u) = [1-u]+
·perceptron loss[9]: l(u) = [-u]+.
·logistic loss[10-11]: l(u) = log(1+exp(-u)).
·exponential loss[12]: l(u) = exp(-u).
·least square loss[13]: l(u) = (1-u)2.
·squared hinge loss[14]: l(u) = ([1-u]+)2.
·LUM loss (large-margin unified machine[15]): for given a>0 and c≥0,
| $ {l_{{\rm{LUM}}}}(u) = \left\{ {\begin{array}{*{20}{l}} {1 - u,}&{{\rm{ if }}\;u \le \frac{c}{{1 + c}},}\\ {\frac{1}{{1 + c}}{{\left( {\frac{a}{{(1 + c)u - c + a}}} \right)}^a},}&{{\rm{ if }}\;u > \frac{c}{{1 + c}}.} \end{array}} \right. $ |
·DWD loss [15-17]: it can be viewed as LUM loss with a = 1 and c = 1, i.e.,
| $ {l_{{\rm{DWD}}}}(u) = \left\{ {\begin{array}{*{20}{l}} {1 - u,}&{{\rm{ if }}\;u \le \frac{1}{2},}\\ {\frac{1}{{4u}},}&{{\rm{ if }}\;u > \frac{1}{2}.} \end{array}} \right. $ | (2) |
Except for perceptron loss, the above-ment-ioned loss functions can be viewed as the surrogate convex envelope of 0-1 loss, which helps to make the loss term be convex and computationally tractable.
For simplicity, we only consider linear form of f to show the penalty term. Assume that f(x) = ωTx+b, where ω = (ω1, …, ωp)T∈
| $ J(f) = \frac{1}{2}\left\| \mathit{\boldsymbol{\omega }} \right\|_2^2 = \frac{1}{2}\sum\limits_{j = 1}^p {\omega _j^2} . $ |
·L1 penalty[18]:
| $ J(f) = {\left\| \mathit{\boldsymbol{\omega }} \right\|_1} = \sum\limits_{j = 1}^p {\left| {{\omega _j}} \right|} . $ |
·Lq penalty[19]:for q≥0,
| $ J(f) = \left\| \mathit{\boldsymbol{\omega }} \right\|_q^q = \sum\limits_{j = 1}^p {{{\left| {{{{ {{ ω}} }}_j}} \right|}^q}} . $ |
·Elastic-net penalty[20]: for α∈[0, 1],
| $ J(f) = \alpha {\left\| \mathit{\boldsymbol{\omega }} \right\|_1} + \frac{{1 - \alpha }}{2}\left\| \mathit{\boldsymbol{\omega }} \right\|_2^2. $ |
There are still many well-known penalties in the literatures such as group LASSO[21], SCAD[22], and MCP[23], which can be used for classification tasks.
The loss term and penalty term have various choices, and their combinations connect several meaningful classifiers. By properly choosing loss function and penalty term, problem (1) can be solved efficiently via the standard convex optimization[24].
2.2 Multicategory classificationThe aforementioned methods are originally designed for binary problems. In practice, it is prevalent to have more than two classes in the dataset. However, generalizations to multicategory case are extremely challenging. To solve a multicategory problem, there exist two common approaches in the literature. One is to solve a sequence of binary problems and combine the results for multicategory classification, e.g., one-versus-rest and one-versus-one[25-26]. This approach is suboptimal in certain situations. One-versus-one method suffers a tie-in-vote problem, and one-versus-rest method is inconsistent when there is no dominating class[27-28]. The other approach is to consider all k classes in one optimization problem simultaneously. One common method to handle k-class problems is to use k decision functions, which represent k different labels. The corresponding prediction rule is based on which function is the maximum.
Let f = (f1, …, fk)T be a vector-valued decision function, which is a mapping from
| $ \begin{array}{*{20}{l}} {\mathop {\min }\limits_{\mathit{\boldsymbol{f}} \in \mathscr{F}} }&{\frac{1}{n}\sum\limits_{i = 1}^n V \left( {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_i}} \right),{y_i}} \right) + \lambda J(\mathit{\boldsymbol{f}}),}\\ {{\rm{ subject\; to }}}&{\sum\limits_{j = 1}^k {{f_j}} (\mathit{\boldsymbol{x}}) = 0,} \end{array} $ | (3) |
with V(·, ·) being a loss function for a multi-category case, and J(f) being a regularization term defined for the decision function. Naturally, J(f) can be designed separately for all k components based on the definitions of penalty in section 2.1. Clearly, when a sum-to-zero constraint is employed for margin-based classifiers, formulation (3) with k = 2 is equivalent to the binary classification problem in (1).
There are several different extensions of binary methods to the multicategory problems. Here, we list several commonly used loss functions as follows.
·Naive hinge loss: V(f, y) = [1-fy]+.
·
·
·
·
·
·
We can abstract two kinds of functional margins for the multicategory classifiers. One is absolute margin, such as those in Refs.[27-28,31-33], which considers fjs separately in additive loss functions. The other is relative margin, e.g., those in Refs. [29-30], which considers the pairwise comparisons {fy-fj, j = 1, …, k, j≠y}. They both encourage the component fy to be larger than the other components under the explicit or implicit sum-to-zero constraint.
Many large margin classifiers may suffer serious drawbacks when the data are noisy, especially when there are outliers in the training data. In Refs. [34-37] the authors showed that the truncation of loss function helps to obtain robust classifiers, such as the truncated hinge loss, truncated exponential loss, and truncated logistic loss. Wu & Liu[38] applied the weighted learning techniques for robust classification performance and efficient computation.
3 Advanced classification methodsFor multicategory classifiers with k decision functions, under the sum-to-zero constraint, its degree of freedom should be k-1, naturally. It can be verified straightforwardly, e.g., only one function is needed for binary classification task. Thus, it should be sufficient to use k-1 functions for k-class problems. The inefficient sum-to-zero constraint makes the optimization problem (3) be more time-consuming and prohibitive. Recently, Zhang & Liu[39] proposed a novel angle-based classification framework without sum-to-zero constraint, which can enjoy better prediction accuracy and faster computational speed. Thus, the angle-based classifiers can be more competitive. We show the details about angle-based classification in section 3.1, and present several recent developments on the angle-based methods in section 3.2.
3.1 Angle-based classificationAngle-based classification considers a k-vertex simplex structure in an Euclidean space
| $ {\mathit{\boldsymbol{W}}_j} = \left\{ {\begin{array}{*{20}{l}} {{{(k - 1)}^{ - \frac{1}{2}}}{\mathit{\boldsymbol{1}}_{k - 1}},}&{j = 1;}\\ { - \frac{{1 + \sqrt k }}{{{{(k - 1)}^{\frac{3}{2}}}}}{\mathit{\boldsymbol{1}}_{k - 1}} + \sqrt {\frac{k}{{k - 1}}} {\mathit{\boldsymbol{e}}_{j - 1}},}&{j \ge 2,} \end{array}} \right. $ |
where 1k-1 is a vector of length k-1 with all entries 1, and ej∈
The angle-based classifier constructs a vector-valued function f = (f1, …, fk-1)T for prediction, which maps x into
For illustration, we demonstrate a toy example to show the procedure of angle-based classification in Fig. 1. The mapped observation
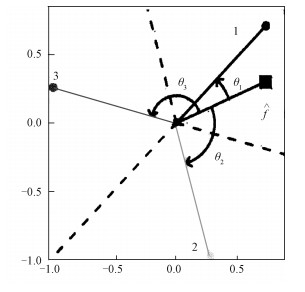
|
Download:
|
|
Fig. 1 The classification regions and prediction rule when k = 3 (from Ref.[39]) |
|
Note that
Motivated by Ref. [39], we propose a general optimization framework for the angle-based classifier as follows
| $ \mathop {\min }\limits_{f \in {\mathscr{F}}} \frac{1}{n}\sum\limits_{i = 1}^n \phi \left( {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_i}} \right),{y_i}} \right) + \lambda J(\mathit{\boldsymbol{f}}), $ | (4) |
where ϕ(f(x), y) is a well-designed loss function for angle-based classification. For example, Ref. [39] used the margin-based loss ϕ = l(〈f(x), Wy〉), where l(·) is an arbitrary binary large-margin loss function, the arguments of ϕ are suppressed in the expressions for simplicity.
One can see that the sum-to-zero constraint can be avoided naturally. With less parameters than problem (3), the framework (4) may become more compact and concise.
3.2 New developmentsNote that the loss functions for multicategory classifiers can be abstracted two types in section 2.2. Analogously, we can extend them to inner product functional margins for angle-based classi-fiers. One is absolute functional margin, which deals with the k inner products {〈f, Wj〉, j = 1, …, k} separately and encourages larger 〈f, Wy〉 and smaller {〈f, Wj〉, j≠y} on the instance (x, y). We consider the following type Ⅰ loss function
| $ \begin{array}{l} {\phi _1} = \gamma {l_1}\left( {\left\langle {\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{x}}),{W_y}} \right\rangle } \right) + \\ \;\;\;\;\;\;(1 - \gamma )\sum\limits_{j \ne y} {{l_2}} \left( { - \left\langle {\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{x}}),{W_j}} \right\rangle } \right), \end{array} $ | (5) |
where l1 and l2 are arbitrary binary margin-based loss functions. The reinforced angle-based multicategory SVM in Ref. [44] followed the loss function (5). Based on the numerical results of Refs. [28,44], the best choice of γ is 1/2 with stable classification performance.
The other is relative functional margin, which handles the difference quantities {〈f, Wy-Wj〉, j≠y}, and encourages larger positive gap for correct classification. We design the type Ⅱ loss as follows,
| $ {\phi _2} = {l_1}\left( {\mathop {\min }\limits_{j \ne y} \left\langle {\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{x}}),{W_y} - {W_j}} \right\rangle } \right). $ | (6) |
The variety of loss functions (5) and (6) contributes to enrich the family of angle-based classifiers. In particular, when γ = 1 in (5), it reduces the original angle-based classifier[39], and they employed the LUM loss for classification under angle-based structure.
Recently, Refs. [44-45] developed the weighted learning techniques for the aforementioned two general angle-based classifiers as follows, the weighted type Ⅰ classifier,
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\mathit{\boldsymbol{f}} \in \mathscr{F}} \lambda J(\mathit{\boldsymbol{f}}) + \frac{1}{n}\sum\limits_{i = 1}^n {\left[ {{\omega _{i,{y_i}}}\gamma {l_1}\left( {\left\langle {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_i}} \right),{W_{{y_i}}}} \right\rangle } \right) + } \right.} }\\ {\left. {(1 - \gamma )\sum\limits_{j \ne {y_i}} {{\omega _{i,j}}} {l_2}\left( { - \left\langle {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_i}} \right),{W_j}} \right\rangle } \right)} \right],} \end{array} $ | (7) |
and the weighted type Ⅱ classifier,
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\mathit{\boldsymbol{f}} \in \mathscr{F}} \frac{1}{n}\sum\limits_{i = 1}^n {{\omega _i}} {l_1}\left( {\mathop {\min }\limits_{j \ne {y_i}} \left\langle {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_i}} \right)} \right.,} \right.}\\ {\left. {\left. {{W_{{y_i}}} - {W_j}} \right\rangle } \right) + \lambda J(\mathit{\boldsymbol{f}}),} \end{array} $ | (8) |
where ωi, j in (7) and ωi in (8) are nonnegative weights for all observations. Reference [45] also show serval strategies for choices of weights.
Denote the truncated loss function of l1(·) and l2(·) be Ts(u) = min(l1(u), l1(s)) and Rv(u) = min(l2(u), l2(v)), where s and v are the corresponding truncation location parameters. Inspired by the truncated loss and robust learning in Refs. [34-37], we devise the truncated ϕ1 and ϕ2 to achieve robust angle-based classification as follows,
| $ \begin{array}{l} \phi _1^t = \gamma {T_s}\left( {\left\langle {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right),{W_y}} \right\rangle } \right) + \\ \;\;\;\;\;\;\;\left( {1 - \gamma } \right)\sum\limits_{j \ne y} {{R_v}\left( { - \left\langle {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right),{W_j}} \right\rangle } \right)} , \end{array} $ | (9) |
and
| $ \phi _2^t = {T_s}\left( {\mathop {\min }\limits_{j \ne y} \left\langle {\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{x}}),{W_y} - {W_j}} \right\rangle } \right). $ | (10) |
For example, Ref. [46] studied the robust angle-based SVMs based on the truncated hinge loss functions, which followed the formulations of truncated loss (9) and (10).
The weighted learning problems for (7) and (8) can be solved by efficient convex optimization techniques, while the robust learning based on the non-convex truncated loss (9) and (10) are more complicated and challenging, which can be solved via difference of convex algorithms[45-46]. They both can enjoy stable performance against potential outliers. Interestingly, the adaptively weighted angle-based classifiers have a close connection with the classifiers based on the truncated loss. Reference [45] showed that the algorithms of weighted learning and truncated learning are equivalent to each other in terms of fixed point.
Recently, we proposed a new family of loss function Vρ(·) as follows,
| $ {V_\rho }(u) = \left\{ {\begin{array}{*{20}{l}} {1 + \frac{1}{\rho }\left[ {1 - {{\rm{e}}^{\rho u}}} \right],}&{{\rm{ if }}\;u \le 0}\\ {{{\rm{e}}^{ - u}},}&{{\rm{ if }}\;u > 0} \end{array}} \right., $ | (11) |
where ρ>0 is a scale parameter. Although Vρ(·) is non-convex and without any truncation, its boundedness property contributes to robust performance. Thus, in order to estimate robust individual treatment rules, we employed Vρ(·) under the angle-based framework (4), and proposed robust outcome weighted learning (ROWL). The proposed ROWL method can enjoy Fisher consistency, and provide estimation for the ratios of two different outcomes. Furthermore, it can yield more competitive performance than some existing methods①.
① This part is from Fu's recent paper "robust outcome weighted learning for optimal individualized treatment rules".
For the disease forecasting problems, there may exist one special variable in the feature space, which needs to be singled out to preserve its effects from other variables, e.g., the age-dependent effect in bioscience. A novel method, targeted local angle-based multicategory SVM (TLAMSVM) was proposed to construct effective age-dependent classification rules. The TLAMSVM method followed the weighted angle-based classification (7). The age-specific prediction rule is very useful to guide personalized treatments②.
② This part is from Zhang's recent paper "targeted local angle-based multi-category support vector machine".
4 Theoretical resultsIn this section, we focus on Fisher consistency, which is a fundamental property of a classifier[47-52]. For multicategory problems with k≥2, the issue of Fisher consistency becomes more complicated. Set the class labels be {1, …, k}. For an observation x, denote the conditional probability be Pj(x) = Pr(Y = j|X = x). Fisher consistency for an angle-based classifier is defined as follows.
Definition 4.1 (Fisher consistency[39,44-46]). Let V(·, ·) be a general margin-based loss function. Suppose f* be the theoretical minimizer of the conditional loss
| $ \arg \mathop {\max }\limits_j \left\langle {{\mathit{\boldsymbol{f}}^*}(\mathit{\boldsymbol{x}}),{W_j}} \right\rangle = \arg \mathop {\max }\limits_j {P_j}(\mathit{\boldsymbol{x}}) $ |
holds, we say that the loss function V and the corres-ponding angle-based classifier is Fisher consistent.
In other words, Fisher consistency means that if we are using infinitely many training instances and an appropriate functional space
Next, we show some results about Fisher consistency for angle-based classifiers in the following theorems.
Theorem 4.1 (Refs. [39,53-54]). Consider the angle-based classification framework (4),
A1.Assume a general margin-based loss ϕ = l(〈f(x), Wy〉). If l′(u) < 0 for all u, it is Fisher consistent.
A2.For the squared error loss function ϕ = ‖f(x)-Wy‖22, it is Fisher consistent.
A3.For the DWD loss ϕ = lDWD(〈f(x), Wy〉) in (2), it is Fisher consistent.
A4.For the new loss ϕ = Vρ(〈f(x), Wy〉) in (11), it is Fisher consistent for ρ>0.
Remark 4.1 A3 and A4 both satisfy the condition of A1, which can be viewed as a special examples of A1.
Denote the hinge loss as Hτ(u) = [τ-u]+ with a parameter τ, the truncated hinge loss as
Theorem 4.2(Refs. [44-46]). Consider the type Ⅰ angle-based loss function (5) and its truncated version (9),
B1.Suppose the reinforced hinge loss be
B2.Suppose
B3.For the reinforced least square loss
B4.If li′(u) < 0 (i = 1, 2) for all u, then the general loss (5) is Fisher consistent for all values of γ∈[0, 1].
B5.If l′i(u) < 0(i = 1, 2) for all u, then the truncated loss (9) is Fisher consistent with γ∈[0, 1], s≤0 and v≤0.
Remark 4.2 Due to the differences between the employed loss functions, case B1-B5 have different consistent intervals for γ. Concretely speaking, the hinge loss in B1 and its truncated version in B2 are non-differentiable at the hinge point and truncation point, thus they may lead to narrower consistent intervals than B3-B5.
Theorem 4.3 (Refs. [37,45-46]). Let l1(·) be a non-increasing loss function with l′1(0) < 0. For the type Ⅱ angle-based loss function (6) and its truncated version (10),
C1.Suppose
C2.The sufficient and necessary condition for Fisher consistency of loss function (6) is
C3.Suppose
C4.For the truncated loss function (10), when k = 2, it is Fisher consistent for all s≤0. While k≥3, the sufficient and necessary condition to ensure Fisher consistency for (10) is that the truncation location s satisfies
Remark 4.3 For the general loss function l1 in (6), C1 and C2 impose two different conditions to achieve Fisher consistency. C1 emphasizes on the conditional class probability, i.e., the existence of dominating class. While C2 restricts the mathematical property of loss function. C3 also fulfills the condition of C4, which can be regarded as a special case of C4.
We summarize the results of Theorem 4.1, 4.2 and 4.3 in Table 1 for a comprehensive view.
|
|
Table 1 Summary of Fisher consistency results for several angle-based classifiers |
In this article we give a brief survey on the statistical classification methods under the regularization framework including binary and multicategory problems, ranging from traditional and advanced methods. The novel angle-based framework connects binary and multicategory problems in a single structure, and can be optimized efficiently without the redundant sum-to-zero constraint. We discuss some new extensions of angle-based classifiers such as robust learning and weighted learning.The theoretical results about Fisher consistency are also presented. We believe that the new angle-based classification and its extensions are very promising research topics.
The angle-based framework opens a door to advanced statistical classification methods, and it will be very interesting and meaningful to generalize this procedure to certain situations. We briefly discuss several suggestions for the future research. Firstly, in a high-dimensional low-sample-size (HDLSS) setting, the multicategory classification problems become more challenging, and the authors of Ref. [54] give a pioneering work as an extension of general DWD to handle multiclass HDLSS case. Secondly, the choice of loss function and the corresponding statistical learning theory are still open to be explored. Thirdly, even though the hard and soft classifiers about the angle-based classification are discussed in Ref. [39], the conditional probability estimation methodology is seldom investigated. Finally, it may be very reasonable to extend the novel angle-based classification to certain fascinating and challenging settings, such as multicategory semi-supervised learning and estimation of dynamic treatment regimes.
| [1] |
Mitchell T M. Machine learning[M]. New York: McGraw-Hill Inc, 1997.
|
| [2] |
Duda R O, Hart P E, Stork D G. Pattern classification[M]. 2nd ed. New York: Wiley-Interscience, 2000.
|
| [3] |
Bishop C M. Pattern recognition and machine learning[M]. New York: Springer, 2006.
|
| [4] |
Hastie T, Tibshirani R, Friedman J. The elements of statistical learning:data mining, inference and prediction[M]. 2nd ed. New York: Springer, 2009.
|
| [5] |
Murphy K P. Machine learning:a probabilistic perspective[M]. Cambridge, MA: MIT press, 2012.
|
| [6] |
Wahba G. Support vector machines, reproducing kernel Hilbert spaces and the randomized GACV[M]//Advances in Kernel Methods-Support Vector Learning: vol 6. Cambridge, MA: MIT Press, 1999: 69-88.
|
| [7] |
Boser B E, Guyon I M, Vapnik V N. A training algorithm for optimal margin classifiers[C]//Proceedings of the fifth annual workshop on computational learning theory. New York: ACM, 1992: 144-152.
|
| [8] |
Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297. |
| [9] |
Rosenblatt F. The perceptron, a perceiving and recognizing automaton project para[M]. Buffalo, NY: Cornell Aeronautical Laboratory, 1957.
|
| [10] |
Cox D R. The regression analysis of binary sequences[J]. Journal of the Royal Statistical Society. Series B, 1958, 20(2): 215-242. |
| [11] |
Walker S H, Duncan D B. Estimation of the probability of an event as a function of several independent variables[J]. Biometrika, 1967, 54(1): 167-179. |
| [12] |
Freund Y, Schapire R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139. DOI:10.1006/jcss.1997.1504 |
| [13] |
Suykens J A, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300. DOI:10.1023/A:1018628609742 |
| [14] |
Chang K W, Hsieh C J, Lin C J. Coordinate descent method for large-scale l2-loss linear support vector machines[J]. Journal of Machine Learning Research, 2008, 9(Jul): 1369-1398. |
| [15] |
Liu Y, Zhang H H, Wu Y. Hard or soft classification Large-margin unified machines[J]. Journal of the American Statistical Association, 2011, 106(493): 166-177. DOI:10.1198/jasa.2011.tm10319 |
| [16] |
Marron J S, Todd M J, Ahn J. Distance-weighted discrimination[J]. Journal of the American Statistical Association, 2007, 102(480): 1267-1271. DOI:10.1198/016214507000001120 |
| [17] |
Marron J S. Distance-weighted discrimination[J]. Wiley Interdisciplinary Reviews:Computational Statistics, 2015, 7(2): 109-114. DOI:10.1002/wics.1345 |
| [18] |
Tibshirani R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society. Series B, 1996, 58(1): 267-288. |
| [19] |
Liu Y, Zhang H H, Park C, et al. Support vector machines with adaptive Lq penalty[J]. Computational Statistics & Data Analysis, 2007, 51(12): 6380-6394. |
| [20] |
Zou H, Hastie T. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society. Series B, 2005, 67(2): 301-320. DOI:10.1111/rssb.2005.67.issue-2 |
| [21] |
Yuan M, Lin Y. Model selection and estimation in regression with grouped variables[J]. Journal of the Royal Statistical Society. Series B, 2006, 68(1): 49-67. DOI:10.1111/rssb.2006.68.issue-1 |
| [22] |
Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. Journal of the American Statistical Association, 2001, 96(456): 1348-1360. DOI:10.1198/016214501753382273 |
| [23] |
Zhang C H. Nearly unbiased variable selection under minimax concave penalty[J]. The Annals of Statistics, 2010, 38(2): 894-942. DOI:10.1214/09-AOS729 |
| [24] |
Boyd S, Vandenberghe L. Convex optimization[M]. New York: Cambridge University Press, 2004.
|
| [25] |
Dietterich T G, Bakiri G. Solving multiclass learning problems via error-correcting output codes[J]. Journal of Artificial Intelligence Research, 1995, 2: 263-286. DOI:10.1613/jair.105 |
| [26] |
Allwein E L, Schapire R E, Singer Y. Reducing multiclass to binary:a unifying approach for margin classifiers[J]. Journal of Machine Learning Research, 2001, 1(2): 113-141. |
| [27] |
Lee Y, Lin Y, Wahba G. Multicategory support vector machines:Theory and application to the classification of microarray data and satellite radiance data[J]. Journal of the American Statistical Association, 2004, 99(465): 67-81. DOI:10.1198/016214504000000098 |
| [28] |
Liu Y, Yuan M. Reinforced multicategory support vector machines[J]. Journal of Computational and Graphical Statistics, 2011, 20(4): 901-919. DOI:10.1198/jcgs.2010.09206 |
| [29] |
Weston J, Watkins C. Support vector machines for multi-class pattern recognition[C]//Proc European Symposium on Artificial Neural Networks: vol 99. Bruges, Belgium: D-Facto public, 1999: 219-224.
|
| [30] |
Crammer K, Singer Y. On the algorithmic implementation of multiclass kernel-based vector machines[J]. Journal of Machine Learning Research, 2002, 2(2): 265-292. |
| [31] |
Tang Y, Zhang H H. Multiclass proximal support vector machines[J]. Journal of Computational and Graphical Statistics, 2006, 15(2): 339-355. DOI:10.1198/106186006X113647 |
| [32] |
Park S Y, Liu Y, Liu D, et al. Multicategory composite least squares classifiers[J]. Statistical Analysis & Data Mining, 2010, 3(4): 272-286. |
| [33] |
Zhang C, Liu Y. Multicategory large-margin unified machines[J]. Journal of Machine Learning Research, 2013, 14(1): 1349-1386. |
| [34] |
Shen X, Tseng G C, Zhang X, et al. On ψ-learning[J]. Journal of the American Statistical Association, 2003, 98(463): 724-734. DOI:10.1198/016214503000000639 |
| [35] |
Liu Y, Shen X. Multicategory ψ-learning[J]. Journal of the American Statistical Association, 2006, 101(474): 500-509. DOI:10.1198/016214505000000781 |
| [36] |
Wu Y, Liu Y. On multicategory truncated hinge loss support vector machines[M]//Prediction and Discovery: AMS-IMS-SIAM Joint Summer Research Conference, Machine and Statistical Learning: volume 443. Snowbird, Utah: American Mathematical Society, 2006: 49-58.
|
| [37] |
Wu Y, Liu Y. Robust truncated hinge loss support vector machines[J]. Journal of the American Statistical Association, 2007, 102(479): 974-983. DOI:10.1198/016214507000000617 |
| [38] |
Wu Y, Liu Y. Adaptively weighted large margin classifiers[J]. Journal of Computational and Graphical Statistics, 2013, 22(2): 416-432. DOI:10.1080/10618600.2012.680866 |
| [39] |
Zhang C, Liu Y. Multicategory angle-based large-margin classification[J]. Biometrika, 2014, 101(3): 625-640. DOI:10.1093/biomet/asu017 |
| [40] |
Hill S I, Doucet A. A framework for kernel-based multi-category classification[J]. Journal of Artificial Intelligence Research, 2007, 30: 525-564. DOI:10.1613/jair.2251 |
| [41] |
Lange K, Wu T. An MM algorithm for multicategory vertex discriminant analysis[J]. Journal of Computational and Graphical Statistics, 2008, 17(3): 527-544. DOI:10.1198/106186008X340940 |
| [42] |
Saberian M J, Vasconcelos N. Multiclass boosting: theory and algorithms[C]//Advances in Neural Information Processing Systems: vol 24. Granada, Spain: Curran Associates, Inc, 2011: 2124-2132.
|
| [43] |
Mroueh Y, Poggio T, Rosasco L, et al. Multiclass learning with simplex coding[C]//Advances in Neural Information Processing Systems: vol 25. Lake Tahoe, Nevada: Curran Associates, Inc, 2012: 2789-2797.
|
| [44] |
Zhang C, Liu Y, Wang J, et al. Reinforced angle-based multicategory support vector machines[J]. Journal of Computational and Graphical Statistics, 2016, 25(3): 806-825. DOI:10.1080/10618600.2015.1043010 |
| [45] |
Fu S, Zhang S, Liu Y. Adaptively weighted large-margin angle-based classifiers[J]. Journal of Multivariate Analysis, 2018, 166: 282-299. DOI:10.1016/j.jmva.2018.03.004 |
| [46] |
Zhang C, Pham M, Fu S, et al. Robust multicategory support vector machines using difference convex algorithm[J]. Mathematical Programming, 2017. DOI:10.1007/s10107-017-1209-5 |
| [47] |
Vapnik V N. Statistical learning theory[M]. New York: Wiley, 1998.
|
| [48] |
Zhang T. Statistical behavior and consistency of classification methods based on convex risk minimization[J]. The Annals of Statistics, 2004, 32(1): 56-85. |
| [49] |
Zhang T. Statistical analysis of some multi-category large margin classification methods[J]. Journal of Machine Learning Research, 2004, 5(Oct): 1225-1251. |
| [50] |
Bartlett P L, Jordan M I, McAuliffe J D. Convexity, classification, and risk bounds[J]. Journal of the American Statistical Association, 2006, 101(473): 138-156. DOI:10.1198/016214505000000907 |
| [51] |
Liu Y. Fisher consistency of multicategory support vector machines[C]//Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics: volume 2. San Juan, Puerto Rico: PMLR, 2007: 291-298.
|
| [52] |
Zou H, Zhu J, Hastie T. New multicategory boosting algorithms based on multicategory Fisher-consistent losses[J]. The Annals of Applied Statistics, 2008, 2(4): 1290. DOI:10.1214/08-AOAS198 |
| [53] |
Zhang C, Lu X, Zhu Z, et al. REC:fast sparse regression-based multicategory classification[J]. Statistics and Its Interface, 2017, 10(2): 175-185. DOI:10.4310/SII.2017.v10.n2.a2 |
| [54] |
Sun H, Craig B A, Zhang L. Angle-based multicategory distance-weighted SVM[J]. Journal of Machine Learning Research, 2017, 18(1): 2981-3001. |
 2019, Vol. 36
2019, Vol. 36 


