2. 中国科学院大学, 北京 100190;
3. 中国国际工程咨询有限公司, 北京 100048
2. University of Chinese Academy of Sciences, Beijing 100190, China;
3. China International Engineering Consulting Corporation, Beijing 100048, China
极化合成孔径雷达(synthetic aperture radar,SAR)利用地物的变极化效应获取描述地物极化散射信息的多维数据,在地物分类[1]、目标检测[2-3]、生物量反演[4-5]等方面有着重要应用,各国都十分重视极化SAR系统的研制和应用。良好的数据质量是极化SAR数据定量化应用的前提,需要对极化数据进行质量评价,并常态化地监测数据质量。幅相不平衡是极化质量评价中十分关心的参数,因此,需要有效的极化SAR幅相不平衡评价方法,以掌握数据质量、把握极化数据应用效果。
目前,对于幅相不平衡的评价,实际中常利用三面角反射器的归一化测量矩阵的VV通道衡量通道间幅相误差的大小。另外定标算法能够计算出幅相不平衡,也可用于质量评价。现有定标算法分为点目标法和分布目标法两种。点目标法直接在特定地区布设已知点目标(定标器),分别有Whitt等[6]提出利用3个无源角反射器的方法以及Freeman等[7]提出利用极化有源定标器的定标法;分布目标法是选用满足互易性和交叉极化与同极化通道不相关等要求的分布目标(定标场),其中,有Van Zyl法[8]、Quegan法[9]、Ainsworth法[10]、最优协方差匹配法[11]等,但利用分布目标只能实现交叉极化通道不平衡的计算,这些方法还需使用一个三面角反射器计算共极化通道不平衡。因此,不管是点目标法还是分布目标法均需依赖于定标器,而定标器存在布设费时费力的问题,并且分布目标定标场,目前公认的只有亚马逊热带雨林的部分区域。总的来说,现有能用于幅相不平衡评价的方法必须依赖于定标器和定标场,导致其存在时间和空间的局限性而无法应用于常态化质量评价。特别是,中国于2016年8月成功发射第一颗全极化SAR遥感卫星——高分3号(GF-3)[12],其数据质量的监测和评价是应用普遍关心的问题,急需一种不依赖于定标器与定标场的幅相不平衡快速评价方法,以满足常态化极化质量监测的需求。
本文基于幅相不平衡评价的研究现状与常态化质量评价的需求,提出不依赖于定标器与定标场、完全基于极化图像中常见分布目标的幅相不平衡快速评价方法。首先,给出该方法对地物散射特性的要求,并采用局部统计求平均、整体求众数的策略,降低其对地物选取的要求。同时,基于数据统计结果,分别总结出满足幅度不平衡和相位不平衡评价要求的地物类型,证实满足要求的地物广泛存在于极化图像中,能够满足常态化质量评价的需求。并通过半物理仿真和GF-3实际数据验证方法的有效性和抗噪性,以及基本不受串扰影响的特性。
1 幅相不平衡评价方法本文主要考虑幅相不平衡的估算问题,在忽略串扰影响情况下,极化失真模型如式(1)所示:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}}&{{\mathit{\boldsymbol{M}}_{{\rm{VH}}}}}\\ {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}}&{{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}} \end{array}} \right] = A{{\rm{e}}^{{\rm{j}}\mathit{\Phi }}}\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&{{f_{\rm{r}}}} \end{array}} \right] \times }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}}&{{\mathit{\boldsymbol{S}}_{{\rm{VH}}}}}\\ {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}}&{{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&{{f_{\rm{t}}}} \end{array}} \right].} \end{array} $ | (1) |
式中:M为测量散射矩阵;A和Φ分别为系统的绝对辐射因子和相位因子;S为地物真实散射矩阵;fr为V接收通道相对于H接收通道的幅相不平衡,即接收通道的幅相不平衡;ft为V发射通道相对于H发射通道的幅相不平衡,即发射通道的幅相不平衡。
基于式(1),可得接收通道的幅度不平衡|fr|L和发射通道的幅度不平衡|ft|L为(见附录)
| $ \left\{ \begin{array}{l} {\left| {{f_{\rm{r}}}} \right|_L} = \frac{1}{2}\left( {\Delta {f_\alpha } - \Delta {f_\beta }} \right) + \frac{1}{2}\left( {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}} \right|}_{\rm{L}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\left( {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VH}}}}} \right|}_{\rm{L}}}} \right),\\ {\left| {{f_{\rm{t}}}} \right|_{\rm{L}}} = \frac{1}{2}\left( {\Delta {f_\alpha } + \Delta {f_\beta }} \right) + \frac{1}{2}\left( {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}} \right|}_{\rm{L}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\left( {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VH}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}} \right|}_{\rm{L}}}} \right). \end{array} \right. $ | (2) |
式中:|·|L=10×log10(〈|·|2〉),〈·〉表示空间求平均,|·|表示求绝对值;Δfα、Δfβ是与地物幅度特性有关的量,即
| $ \left\{ \begin{array}{l} \Delta {f_\alpha } = {\left| {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}} \right|_{\rm{L}}} - {\left| {{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \right|_{\rm{L}}},\\ \Delta {f_\beta } = {\left| {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}} \right|_{\rm{L}}} - {\left| {{\mathit{\boldsymbol{S}}_{{\rm{VH}}}}} \right|_{\rm{L}}}. \end{array} \right. $ | (3) |
同理,得到接收通道的相位不平衡θr与发射通道的相位不平衡θt分别表示为(见附录)
| $ \left\{ \begin{array}{l} {\theta _{\rm{r}}} = \frac{1}{2}\left( {\Delta {\theta _\alpha } + \Delta {\theta _\beta }} \right) + \frac{1}{2}P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}\mathit{\boldsymbol{M}}_{{\rm{VH}}}^ * } \right\rangle } \right) - \\ \;\;\;\;\;\;\frac{1}{2}P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}\mathit{\boldsymbol{M}}_{{\rm{VV}}}^ * } \right\rangle } \right),\\ {\theta _t} = \frac{1}{2}\left( {\Delta {\theta _\alpha } + \Delta {\theta _\beta }} \right) - \frac{1}{2}P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}\mathit{\boldsymbol{M}}_{{\rm{VH}}}^ * } \right\rangle } \right) - \\ \;\;\;\;\;\;\frac{1}{2}P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}\mathit{\boldsymbol{M}}_{{\rm{VV}}}^ * } \right\rangle } \right). \end{array} \right. $ | (4) |
式中:P表示复数的相位;Δθα、Δθβ是与地物相位特性相关的量,即
| $ \left\{ \begin{array}{l} \Delta {\theta _\alpha } = P\left( {\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}\mathit{\boldsymbol{S}}_{{\rm{VV}}}^ * } \right\rangle } \right),\\ \Delta {\theta _\beta } = P\left( {\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}\mathit{\boldsymbol{S}}_{{\rm{VH}}}^ * } \right\rangle } \right). \end{array} \right. $ | (5) |
若地物的幅度特性Δfα、Δfβ约为0,则可利用实测散射矩阵M通过式(6)估计得到幅度不平衡|fr|L、|ft|L;若相位特性Δθα、Δθβ约为0,则可利用实测散射矩阵M通过式(7)估计得到相位不平衡θr、θt。
| $ \left\{ \begin{array}{l} {\left| {{f_{\rm{r}}}} \right|_{\rm{L}}} = \frac{1}{2}\left( {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}} \right|}_{\rm{L}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VH}}}}} \right|}_{\rm{L}}}} \right),\\ {\left| {{f_{\rm{t}}}} \right|_{\rm{L}}} = \frac{1}{2}\left( {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}} \right|}_{\rm{L}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{{\left| {{\mathit{\boldsymbol{M}}_{{\rm{VH}}}}} \right|}_{\rm{L}}} - {{\left| {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}} \right|}_{\rm{L}}}} \right). \end{array} \right. $ | (6) |
| $ \left\{ \begin{array}{l} {\theta _{\rm{r}}} = \frac{1}{2}\left( {P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}\mathit{\boldsymbol{M}}_{{\rm{VH}}}^ * } \right\rangle } \right) - P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}\mathit{\boldsymbol{M}}_{{\rm{VV}}}^ * } \right\rangle } \right)} \right),\\ {\theta _t} = - \frac{1}{2}\left( {P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}\mathit{\boldsymbol{M}}_{{\rm{VH}}}^ * } \right\rangle } \right) + P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}\mathit{\boldsymbol{M}}_{{\rm{VV}}}^ * } \right\rangle } \right)} \right). \end{array} \right. $ | (7) |
由式(2)、式(4)可知,质量评价允许|fr|L、|ft|L的估算误差在0.3dB以内以及θr、θt的估算误差在4°以内,则只需要求Δfα、Δfβ绝对值均小于0.3dB,Δθα、Δθβ的绝对值均小于4°。因此,只需要分别寻找满足式(8)和式(9)的地物来实现幅度不平衡和相位不平衡的估算。
| $ \left\{ \begin{array}{l} \left| {\Delta {f_\alpha }} \right| < 0.3\;{\rm{dB,}}\\ \left| {\Delta {f_\beta }} \right| < 0.3\;{\rm{dB}}{\rm{.}} \end{array} \right. $ | (8) |
| $ \left\{ \begin{array}{l} \left| {\Delta {\theta _\alpha }} \right| < {4^ \circ }{\rm{,}}\\ \left| {\Delta {\theta _\beta }} \right| < {4^ \circ }{\rm{.}} \end{array} \right. $ | (9) |
|Δfβ| < 0.3dB和|Δθβ| < 4°代表地物的交叉极化通道满足较弱的散射互易,对于单站SAR来说,比较容易满足。因此,幅相不平衡的估算主要受到Δfα、Δθα的影响。而|Δfα| < 0.3dB和|Δθα| < 4°代表地物HH极化与VV极化的幅度在空间平均后差异较小,相位差在空间平均后接近0,可以理解为地物的同极化通道满足弱互易性。为寻找满足要求的地物,对含森林、城市、农田、裸地、海洋等典型地物的11景RadarSat-2已校正全极化数据进行分析,图 1展示4组典型结果,图 1(a)~1(d)为各数据的伪彩色合成图;图 1(e)~1(h)为幅度特性(Δfα、Δfβ)的统计结果,其中满足式(8)即交叉极化和同极化幅值均满足弱互易性的地物被标记为红色;图 1(i)~1(l)为相位特性(Δθα、Δθβ)的统计结果,其中满足式(9)即交叉极化和同极化相位均满足弱互易性的地物被标记为红色。首先,如图 1(e)~1(h)所示,对于幅度不平衡的估计,海洋、城市地区明显不满足要求,农田、裸地等地物有极少区域满足,大部分成片林木覆盖区域能够满足,这与文献[13]指出的大部分森林地区或大部分体散射机制地物能够满足方位对称性,即Δfα≈0一致,因此,可选择成片林木覆盖区域用于幅度不平衡的快速评价。对于相位不平衡的估计,Freeman分解[14]中体散射模型的〈SHHSVV*〉=1/3,即体散射机制的地物满足Δθα≈0,另外文献[15]也指出土壤等略微粗糙的自然地物区域在入射角小于60°时,Δθα≈0,这与图 1(i)~1(l)所示一致,即除城市地区外的其他自然地物区域(包括裸地、农田、森林、水体)均能满足相位不平衡估计的要求,但海洋地区在入射角较大时Δθα值较高,除非垂直入射,否则不应该选择海洋地区进行相位不平衡的估算[15],因此,本文选择非水体的自然地物区域进行相位不平衡的估算,更具可靠性和适用性。同时,从图 1中可以看出用于幅相不平衡估计的地物在极化图像中普遍存在。

|
Download:
|
| 图 1 4组数据的伪彩色图和满足幅相不平衡估算要求的地物的分布情 Fig. 1 Pseudo-color images of four groups of data and the results of ground objects satisfying the requirements of channel imbalance estimation | |
总的来说,可以在待评价极化图像中选择成片林木覆盖区域,利用式(6)估算出幅度不平衡,以及选择非水体的自然地物区域,利用式(7)估算相位不平衡。从图 1可以看出,在满足要求的区域内会有少数像素点不满足要求,称为坏点,为避免这些少数坏点影响估算结果,本文对选择的地物区域进行分块,每个数据块可估算出一组幅相不平衡,再把整个区域中出现频率最高(众数)的幅相不平衡,作为最终结果。地物选择是否合适会影响最后的评价结果,而本方法采用局部求平均、整体求众数的统计计算,只需要选取的区域中以林木覆盖区域或非水体自然地物区域为主,这样的区域在极化SAR图像中比较容易找到,因此该统计计算减弱了地物选取对评价结果的影响,也放宽了对所选区域的限制。另外,文献[15-16]利用满足互易性以及HH和VV相位差为0的地物进行相位定标,其主体思路虽与本文相位不平衡估计方法一致,但本文通过实验分析和统计计算降低了该类方法对地物的要求,实现了相位不平衡的常态化估计。
基于普通分布目标的幅相不平衡评价方法的具体流程如下:
步骤1:在待评价的极化SAR数据中选取以成片林木覆盖/非水体自然地物为主的区域M,将所选区域进行分块,距离向和方位向的分块大小均选取20~100个像素点,得到N个大小相同的数据块MN,N一般大于200;
步骤2:计算每个数据块的|MHH|L、|MHV|L、|MVH|L、|MVV|L值以及P (〈MHHMVV*〉)、P(〈MHVMVH*〉)值;
步骤3:针对每个数据块,利用式(6)、式(7)计算出使用该数据块所估算出的幅度不平衡值(dB),记为|fr, N|L、|ft, N|L,以及相位不平衡值,记为θr, N、θt, N;
步骤4:将步骤3中所得的幅度不平衡结果|fr, N|L、|ft, N|L以及相位不平衡结果θr, N、θt, N进行统计,分别得到直方图Hfr、Hft、Hθr、Hθt,并将出现频次最多的幅相不平衡作为最终的幅相不平衡值,如式(10)、式(11)。
| $ \left\{ \begin{array}{l} {\left| {{f_{\rm{r}}}} \right|_{\rm{L}}} = H_{f{\rm{r}}}^{ - 1}\left( {\max \left( {{H_{f{\rm{r}}}}} \right)} \right),\\ {\left| {{f_{\rm{t}}}} \right|_{\rm{L}}} = H_{f{\rm{t}}}^{ - 1}\left( {\max \left( {{H_{f{\rm{t}}}}} \right)} \right). \end{array} \right. $ | (10) |
| $ \left\{ \begin{array}{l} {\theta _{\rm{r}}} = H_{\theta {\rm{r}}}^{ - 1}\left( {\max \left( {{H_{\theta {\rm{r}}}}} \right)} \right),\\ {\theta _{\rm{t}}} = H_{\theta {\rm{t}}}^{ - 1}\left( {\max \left( {{H_{\theta {\rm{t}}}}} \right)} \right). \end{array} \right. $ | (11) |
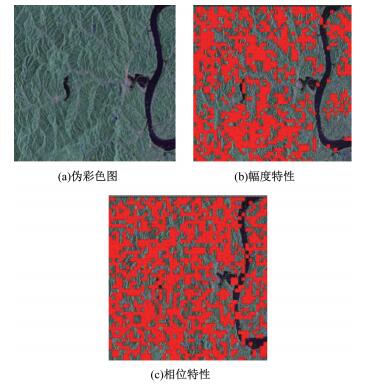
RadarSat-2的全极化数据是全球公认的高质量极化数据,向RadarSat-2的已校正全极化图像中加入不同程度的幅相不平衡模拟失真。该部分选用中国江西地区RadarSat-2全极化图像验证方法的有效性、抗噪性,并证实该方法不受串扰影响,其大小为2000像素×2000像素,图 2(a)展示该实验地区的伪彩色图像,图 2(b)、2(c)分别展示该地区的幅度特性和相位特性,其含义与图 1一致。为简化分析,假设fr=ft=f。且实验部分涉及区域分块时,分块大小均为100像素×100像素。
|
Download:
|
| 图 2 实验数据的伪彩色图及散射特性 Fig. 2 Pseudo-color image and the scattering characteristics of the test data | |
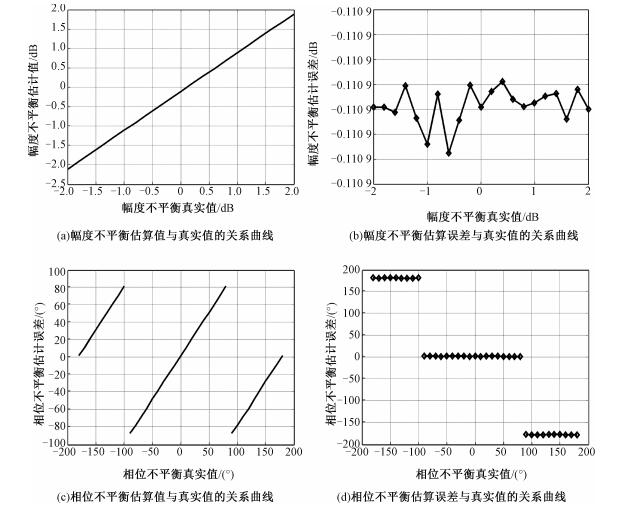
向所选实验数据中加入不同程度的幅度不平衡(-2~2 dB)、相位不平衡(-180°~180°),模拟实际场景里的测量失真,并利用本文方法对幅相不平衡进行估算,得到f的估计值和真实值之间的关系曲线(如图 3(a)、3(c))以及估计误差与真实值之间的关系曲线(见图 3(b)、3(d))。
|
Download:
|
| 图 3 幅度不平衡与相位不平衡的估算结果 Fig. 3 Estimate results of channel and phase imbalances | |
从图 3(a)、3(b)可以看出,使用该区域进行幅度不平衡估计时,估算误差在0.1dB左右,代表该实验区域的幅度特性满足式(8),同时也证实本文方法通过选择合适的地物,能将f的幅度估算误差控制在0.3dB以内;从图 3(c)、3(d)的相位不平衡估算结果发现,由于相位模糊,当相位不平衡绝对值大于π/2时,估算值与真实值之间存在π的误差,如果不考虑相位模糊的影响,估计值和真实值间的误差在1°以内。文献[16]指出,该误差在实际中影响很微小,仅仅引起45°线极化成分被译解成135°线极化,或者相反。
为分析相位模糊引起的估算误差对实际应用的影响,本文利用Pauli、SDH、Freeman等分解方法对森林、农田、裸地、水体、建筑等5种典型地物各散射机制所占百分比进行分析,得到无误差以及存在180°相位不平衡时各散射机制百分比的差异值(%),如表 1所示。从表 1的结果可以看出,存在该误差与无误差时地物各散射机制的占比差异大部分很小(< 0.5%),初步证实相位模糊引起的接收和发射通道相位不平衡180°的估算误差对极化分解的影响较小,与文献[16]中的结论一致。并且,本文方法的提出是为满足常态化极化数据质量监测需求,不必达到定标方法的精度。因此,虽然存在相位模糊,但本文方法所得到的相位不平衡评价结果能够反映出极化图像的相位失真程度,达到质量监测的要求。半物理仿真实验,验证了本文提出的幅相不平衡快速评价方法能够正确反映极化图像的幅相误差。
|
|
表 1 无相位误差和存在180°相位误差下各地物散射机制占比的差异值 Table 1 Differences in proportion of scattering mechanisms between the cases of no phase error and 180° phase error |
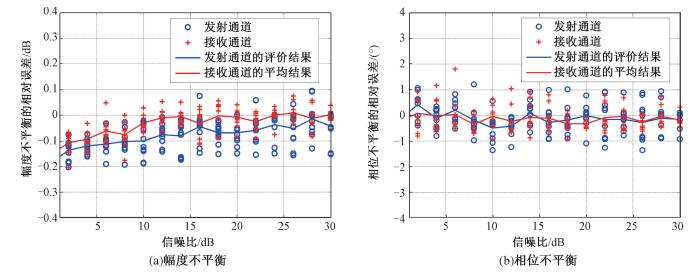
在验证有效性的同时分析本文方法的抗噪性,为此,向接收和发射通道均存在1.5dB幅度不平衡和20°相位不平衡的模拟失真数据中加入不同程度(1~30dB)的加性高斯噪声,进行10次随机实验,得到在不同信噪比下,10次实验的幅相不平衡估算值与无噪声影响的估计值间的相对误差,如图 4所示。其中图 4(a)为不同信噪比下接收通道和发射通道幅度不平衡的相对误差,图 4(b)为相位不平衡的相对误差。
|
Download:
|
| 图 4 幅相不平衡估计误差随信噪比的变化曲线 Fig. 4 Variations in estimate error of channel imbalances with the signal-noise ratio | |
如图 4(a)、4(b)所示,接收通道和发射通道的幅相不平衡相对误差随信噪比的变化趋势一致。随着信噪比的下降,幅度不平衡相对误差的绝对值增大,即噪声的增大导致估计不准确,但当信噪比大于10dB时,该相对误差很小,基本在±0.1dB以内。对于相位不平衡的估计,随着信噪比的减小,相位不平衡的相对误差一直保持在0值附近,基本不受信噪比变差的影响,这是由于相位不平衡估算利用的是HV和VH以及HH和VV间的相位差异,以HV和VH举例,二者共轭乘积求平均后,噪声项为〈NHVNVH*〉,而通道间噪声的相关性较小,并且空间平均使噪声项的影响减小,因此噪声基本不会影响相位不平衡的评估。综合图 4(a)与4(b)的结果得到,在信噪比大于10dB时,本方法能够不受噪声的影响,正确反映图像中的幅相不平衡。本文方法选取的林木覆盖或草地等区域信噪比一般大于10dB,因此该方法能够取得较好的效果。
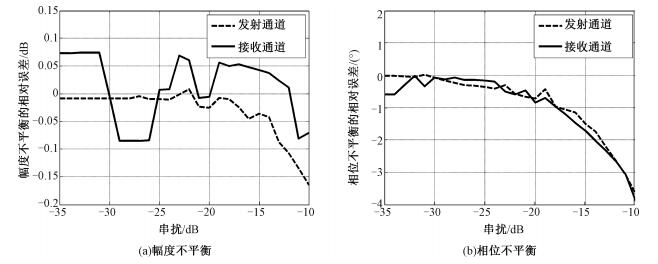
2.1.3 串扰的影响实际系统中会存在串扰影响极化测量,在此,实验分析串扰对幅相不平衡评价的影响。向接收和发射通道均存在1.5dB幅度不平衡和20°相位不平衡的模拟失真数据中加入不同程度的串扰(-35~-10dB),并使用本文方法进行幅相不平衡评价,得到不同串扰下,幅相不平衡估计值和无串扰影响的估计值间的相对误差(图 5)。
|
Download:
|
| 图 5 幅相不平衡估算误差值随串扰的变化曲线 Fig. 5 Variations in estimate error of channel imbalances with the crosstalk | |
从图 5(a)可以看出,接收通道幅度不平衡的相对误差随串扰的波动比发射通道的大,因为对于本文所选的实验数据,幅度不平衡的统计直方图存在多个峰值,串扰的存在导致评估结果在多个峰值间波动,而接收通道Hfr多个峰值间的差异大于发射通道Hft峰值间的差异。虽然存在波动,但在串扰小于-15dB时,接收通道和发射通道幅度不平衡的相对误差均控制在±0.1dB以内。如图 5(b)所示,串扰对接收通道和发射通道相位不平衡估计的影响一致,串扰的增大导致估计偏差增大;在串扰小于-14dB时,串扰对相位不平衡估算的影响小于2°。因此,串扰低于-15dB时,幅度不平衡的相对误差小于0.1dB,相位不平衡的相对误差小于2°,而一般的系统串扰不会超过-15dB,因此,该方法能够用于存在串扰失真的极化数据。
2.2 实测数据实验实际中用三面角反射器VV和HH极化间的幅度差异和相位差异分别评估幅度不平衡和相位不平衡。在此,使用本文提出的方法和三面角反射器法对GF-3的2景未进行极化校正的数据进行幅相不平衡评价,验证方法的有效性,其中,选取的自然地物区域见图 6(a)、6(b),布设的角反射器如图 6(c)、6(d)所示,得到的接收和发射通道总的幅相不平衡评估值,即|fr|L+|ft|L与θr+θt的值,如表 2所示。

|
Download:
|
| 图 6 本文方法所选自然地物区域的伪彩图和含定标器的单极化数据图 Fig. 6 Pseudo-color images of selected nature area and the single-polarized images with calibrators | |
|
|
表 2 GF-3定标场角反射器和本文方法质量评价结果 Table 2 Quality assessment results of GF-3 calibration field by calibrators and the proposed method |
表 2结果显示,该方法估算的幅相不平衡评价结果与角反射器的提取结果虽有一定差异,但幅度不平衡的差异值在0.3dB以内,相位不平衡的差异值在8°以内,能够满足极化SAR数据质量评价对幅相误差评估的要求,二者所反映的幅相不平衡失真水平基本一致。GF-3的实际数据验证了本文方法能够有效地反映极化数据的幅相误差。需说明本文提出的方法不是要替代三面角反射器法,而是针对常态化质量评价的需求,给出能够不受时间和空间限制的幅相不平衡评价方法。
3 总结本文基于常见地物类型的散射特性分析,提出一种基于普通分布目标的极化SAR幅相不平衡快速评价方法,并利用RadarSAT-2全极化数据和GF-3的定标场数据验证该方法的有效性与抗噪性,同时证实该方法能够用于受串扰影响的极化数据中。该方法不依赖于定标器与定标场,选取极化图像中的常见分布目标用于幅相不平衡的评价,采用局部统计求平均、整体求众数,放宽其对地物的要求,为长期监测能够衡量极化数据质量的幅相不平衡指标提供有效手段,实现便捷常态化的幅相不平衡评价。
附录在此详细推导式(2)和式(4)。
首先,展开式(1),得
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{M}}_{{\rm{HH}}}} = A{{\rm{e}}^{{\rm{j}}\mathit{\Phi} }}{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}\\ {\mathit{\boldsymbol{M}}_{{\rm{HV}}}} = A{{\rm{e}}^{{\rm{j}}\mathit{\Phi} }}{f_{\rm{r}}}{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}\\ {\mathit{\boldsymbol{M}}_{{\rm{VH}}}} = A{{\rm{e}}^{{\rm{j}}\mathit{\Phi} }}{f_{\rm{t}}}{\mathit{\boldsymbol{S}}_{{\rm{VH}}}}\\ {\mathit{\boldsymbol{M}}_{{\rm{VV}}}} = A{{\rm{e}}^{{\rm{j}}\mathit{\Phi} }}{f_{\rm{r}}}{f_{\rm{t}}}{\mathit{\boldsymbol{S}}_{{\rm{VV}}}} \end{array} \right.. $ | (A1) |
则M的4个极化分量各自的共轭乘积并求空间平均后,得到4个等式,如下:
| $ \left\{ \begin{array}{l} |\left\langle {|{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}{|^2}} \right\rangle | = {A^2}|\left\langle {|{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}{|^2}} \right\rangle |\\ |\left\langle {|{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}{|^2}} \right\rangle | = {A^2}|{f_{\rm{r}}}{|^2} \times |\left\langle {|{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}{|^2}} \right\rangle |\\ |\left\langle {|{\mathit{\boldsymbol{M}}_{{\rm{VH}}}}{|^2}} \right\rangle | = {A^2}|{f_{\rm{t}}}{|^2} \times |\left\langle {|{\mathit{\boldsymbol{S}}_{{\rm{VH}}}}{|^2}} \right\rangle |\\ |\left\langle {|{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}{|^2}} \right\rangle | = {A^2}|{f_{\rm{r}}}{|^2}|{f_{\rm{t}}}{|^2} \times |\left\langle {|{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}{|^2}} \right\rangle | \end{array} \right.. $ | (A2) |
式中,〈·〉表示空间求平均,|·|表示求绝对值。
对式(A2)等式两边取对数,则有
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}} = \mathit{\boldsymbol{|}}A{\mathit{\boldsymbol{|}}_{\rm{L}}} + \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}}\\ \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}} = \mathit{\boldsymbol{|}}A{\mathit{\boldsymbol{|}}_{\rm{L}}} + \mathit{\boldsymbol{|}}{f_{\rm{r}}}{\mathit{\boldsymbol{|}}_L} + \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}}\\ \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{M}}_{{\rm{VH}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}} = \mathit{\boldsymbol{|}}A{\mathit{\boldsymbol{|}}_{\rm{L}}} + \mathit{\boldsymbol{|}}{f_{\rm{t}}}{\mathit{\boldsymbol{|}}_L} + \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{S}}_{{\rm{VH}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}}\\ \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}} = \mathit{\boldsymbol{|}}A{\mathit{\boldsymbol{|}}_{\rm{L}}} + \mathit{\boldsymbol{|}}{f_{\rm{r}}}{\mathit{\boldsymbol{|}}_L} + \mathit{\boldsymbol{|}}{f_{\rm{t}}}{\mathit{\boldsymbol{|}}_\rm{L}} + \mathit{\boldsymbol{|}}{\mathit{\boldsymbol{M}}_{{\rm{VV}}}}{\mathit{\boldsymbol{|}}_{\rm{L}}} \end{array} \right.. $ | (A3) |
式中,|·|L的含义与式(2)中的一致。
利用式(A3)的4个等式求解方程,即得到式(2)。
再根据式(A1),可以得到
| $ \left\{ \begin{array}{l} \left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}\mathit{\boldsymbol{M}}_{{\rm{VH}}}^*} \right\rangle = {A^2}{f_{\rm{r}}}f_{\rm{t}}^{\rm{*}}\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}\mathit{\boldsymbol{S}}_{{\rm{VH}}}^*} \right\rangle \\ \left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}\mathit{\boldsymbol{M}}_{{\rm{VV}}}^*} \right\rangle = {A^2}f_{\rm{r}}^{\rm{*}}f_{\rm{t}}^{\rm{*}}\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}\mathit{\boldsymbol{S}}_{{\rm{VV}}}^*} \right\rangle \end{array} \right.. $ | (A4) |
对式(A4)的等式两边求相位,记P为复数的相位,得
| $ \left\{ \begin{array}{l} P\left( {\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HV}}}}\mathit{\boldsymbol{M}}_{{\rm{VH}}}^*} \right\rangle } \right) = P({f_{\rm{r}}}) - P({f_{\rm{t}}}) + P(\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}\mathit{\boldsymbol{S}}_{{\rm{VH}}}^*} \right\rangle )\\ P(\left\langle {{\mathit{\boldsymbol{M}}_{{\rm{HH}}}}\mathit{\boldsymbol{M}}_{{\rm{VV}}}^*} \right\rangle ) = - P({f_{\rm{r}}}) - P({f_{\rm{t}}}) + P(\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}\mathit{\boldsymbol{S}}_{{\rm{VV}}}^*} \right\rangle ) \end{array} \right.. $ | (A5) |
再利用式(A5)的2个等式求解方程,即得到式(4)。
| [1] |
折小强, 仇晓兰, 雷斌, 等. 一种极化熵结合混合GEV模型的全极化SAR潮间带区域地物分类方法[J]. 雷达学报, 2017, 6(5): 554-563. |
| [2] |
张妙然, 刘畅. 基于特征筛选和二级分类的极化SAR建筑提取算法[J]. 中国科学院大学学报, 2018, 35(1): 89-95. |
| [3] |
文伟, 王英华, 冯博, 等. 基于监督非相干字典学习的极化SAR图像舰船目标检测[J]. 自动化学报, 2015, 41(11): 1926-1940. |
| [4] |
Liu J, Liao J J, Shen G Z. Retrieval of wetland vegetation biomass in Poyang Lake based on quad-polarization image[J]. Remote Sensing for Land and Resources, 2012, 24(3): 38-43. |
| [5] |
Yuzugullu O, Erten E, Hajnsek I. Estimation of rice crop height from X-and C-band PolSAR by metamodel-based optimization[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(1): 194-204. DOI:10.1109/JSTARS.2016.2575362 |
| [6] |
Whitt M W, Ulaby F T, Polatin P, et al. A general polarimetric radar calibration technique[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(1): 62-67. DOI:10.1109/8.64436 |
| [7] |
Freeman A, Shen Y, Werner C L. Polarimetric SAR calibration experiment using active radar calibrators[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(2): 224-240. DOI:10.1109/36.46702 |
| [8] |
Van Zyl J J. Calibration of polarimetric radar images using only image parameters and trihedral corner reflector responses[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(3): 337-348. DOI:10.1109/36.54360 |
| [9] |
Quegan S. A unified algorithm for phase and cross-talk calibration of polarimetric data-theory and observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(1): 89-99. DOI:10.1109/36.285192 |
| [10] |
Ainsworth T L, Ferro-Famil L, Lee J S. Orientation angle preserving a posteriori polarimetric SAR calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(4): 994-1003. DOI:10.1109/TGRS.2005.862508 |
| [11] |
Villa A, Iannini L, Giudici D, et al. Calibration of SAR polarimetric images by means of a covariance matching approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(2): 674-686. |
| [12] |
丁赤飚, 刘佳音, 雷斌, 等. 高分三号SAR卫星系统级几何定位精度初探[J]. 雷达学报, 2017, 6(1): 11-16. |
| [13] |
Souyris J C, Imbo P, Fjortoft R, et al. Compact polarimetry based on symmetry properties of geophysical media:the/spl pi//4 mode[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 634-646. DOI:10.1109/TGRS.2004.842486 |
| [14] |
Freeman A, Durden S L. A three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973. DOI:10.1109/36.673687 |
| [15] |
Guissard A. Phase calibration of polarimetric radars from slightly rough surfaces[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(3): 712-715. DOI:10.1109/36.297991 |
| [16] |
Zebker H A, Lou Y. Phase calibration of imaging radar polarimeter Stokes matrices[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 28(2): 246-252. |
 2019, Vol. 36
2019, Vol. 36 


