2. 中国科学院大学, 北京 100049;
3. 中国国际工程咨询公司, 北京 100048
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. China International Engineering Consulting Corporation, Beijing 100048, China
高光谱图像一般含有数十至数百个波段,其数据可以看作是一个三维立方体,其中每一个像素点抽取出来都是一条连续的光谱曲线,相邻波段之间的波长相差为纳米级,其精细的光谱分辨率使得高光谱图像应用越来越广泛[1],例如在地质制图、矿石寻找、环境大气监测、农林森林调查、海洋生物研究与海水分析等领域都有重要应用[2]。随着高光谱图像应用越来越广泛,其图像分析处理也变得越来越重要。高光谱图像分类是其信息分析的重要手段之一,分类主要有两种,有监督分类和无监督分类。有监督分类方法众多,如SAM[3]、最大似然[4]、SVM[5]和神经网络[6]等方法,分类精度随着方法的发展越来越高,但是有监督的分类必须以图像存在样本标签为前提。而在实际应用中,获得的高光谱图像往往是没有先验信息的,在这种情况下,无监督聚类就显得十分重要[7]。
在实际应用中,常用的无监督聚类方法有K-means算法[8-9]、均值漂移(mean-shift)算法[10]、迭代自组织数据分析(ISODATA)算法[11]和DBSCAN(density-based spatial clustering of applications with noise)方法[12]等。其中,K-means算法和ISODATA算法对于初始值的选取十分敏感,容易陷入局部最优,且只有在数据为球状或者接近球状时聚类效果较好;Mean-Shift算法时间复杂度高,且半径参数的选取会对聚类结果产生很大的影响;DBSCAN方法虽然不用指定最终聚类类别数目,但是当空间聚类的密度不均匀、聚类间距差相差很大时,邻域半径和对象邻域内样本数量阈值选取困难,聚类质量较差。近年来,谱聚类方法[13-14]在众多聚类算法中显示出聚类精度高稳定性好的优势,其应用也越来越广泛,但是在高光谱图像中很少见到谱聚类算法的应用。谱聚类方法进行聚类的关键是数据间相似度矩阵的构造以及特征值和特征向量的求解,相似度矩阵的大小取决于参与聚类的样本个数,当数据量非常大时,该矩阵占有很大的内存,且特征值的求解面临巨大压力,所以该方法适用于样本量较少的数据,而高光谱图像的数据量非常大,致使谱聚类方法无法在高光谱图像聚类中进行应用。针对这一问题,本文提出结合K-Means的谱聚类方法(K-means spectral clustering,KSC),有效结合K-means算法,将谱聚类应用到高光谱图像中,对其实现较高总体分类精度的聚类。
1 谱聚类方法谱聚类方法是一种基于图的聚类方法,能够对任意形状的数据进行最优划分。由于这一优点,这些年谱聚类方法的应用领域越来越广泛。谱聚类算法以图论为基础,所有数据可以看成是无向带权图
对于输入的具有m个数据点的数据集,
| $ {w_{ij}} = \left\{ \begin{array}{l} {\rm{exp}} - \frac{{\parallel {x_i} - {x_j}{\parallel ^2}}}{{{\sigma ^2}}}, \;\;\;i \ne j\\ \;\;\;\;\;\;\;\;0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;i = j \end{array} \right., $ | (1) |
式中:σ为尺度参数,本文中σ的大小按照Zelnik-Manor和Perona在Self-Tuning谱聚类方法[15]中提出的“local Scaling”思想进行选取。
记矩阵D为度矩阵,度矩阵为对角矩阵,将W的每行元素相加得到度矩阵D。记
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{D}} - \mathit{\boldsymbol{W}}. $ | (2) |
假定
| $ {\rm{Cut}}\left( {A, B} \right) = \sum\limits_{i \in A, j \in B} {} {w_{ij}}, $ | (3) |
比例割(Ratio Cut)函数[16]为
| $ {\rm{Rcut}}\left( {A, B} \right) = \frac{{{\rm{Cut}}\left( {A, B} \right)}}{{|A|}} + \frac{{{\rm{Cut}}\left( {A, B} \right)}}{{|B|}}, $ | (4) |
式中:|A|为A类数据点数目,|B|为B类数据点数目。显然最小化比例割对应着一个最佳的二分类问题。假定有m维向量
| $ {\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{Lf}} = |V|{\rm{Rcut}}\left( {A, B} \right), $ | (5) |
式中:|V|表示数据样本点数量。对于2类比例割谱聚类转化为如下模型
| $ \left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{f}} {\rm{Tr}}\left( {{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{Lf}}} \right)\\ {\rm{s}}{\rm{.t}}{\mathit{\boldsymbol{f}}^{\rm{T}}}{\bf{1}} = 0, {\rm{ }}{\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{f}} = m \end{array} \right., $ | (6) |
其中Tr为矩阵的迹。对于k类问题,比例割优化模型为
| $ \left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{H}} \in {\mathbb{R}^{m \times k}}} {\rm{Tr}}({\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{LH}})\\ {\rm{s}}{\rm{.t}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}} = \mathit{\boldsymbol{I}} \end{array} \right., $ | (7) |
模型(7)是一个标准的求解迹最小化问题,根据拉普拉斯矩阵性质,该优化问题最优解可转化为求L矩阵最小的k-1个特征值对应的特征向量。
对于一幅M×N×L大小的高光谱图像,建立的相似度矩阵大小为(M×N)2,如果矩阵中每个值按照1个字节来计算,那么该矩阵所需内存约(M×N)2×10-9G。以实际高光谱图像举例,如果一幅高光谱图像大小为500×500×200,那么相似度矩阵为25万×25万,所需计算机内存约为62.5G,这是一般PC机无法承受的。针对这一问题,本文提出相应的解决方法。
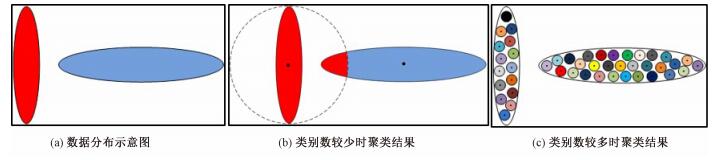
2 K均值-谱聚类方法K均值-谱聚类(K-means spectral clustering,KSC)方法是结合K-means算法与谱聚类方法的优点而实现聚类的一种方法。K-means算法对初始值选取敏感而易陷入局部最优,致使当聚类类别数较少时,整体的分类精度较低,而当聚类类别数非常多时,局部的分类精度较高。如对于图 1(a)所示的数据分布示意图进行K-means算法聚类,当聚类类别数较少,如图 1(b)所示分为2类时,由于K-means算法以距离为分类判别准则,对于该形状分布的数据,K-means算法会出现错分情况,如图中虚线圆内的右侧红色部分错分;当聚类类别数较多,如图 1(c)所示分为很多类时,对于分成的每一类其类内分类精度都比较高。如此,可以利用这一点,首先对高光谱图像数据进行K-means聚类,将其聚成很多类,从而可得到相应类别数的聚类中心,该聚类中心可作为相应类别的代表,接下来可以对其进行谱聚类处理,这样的处理在不损害聚类精度的同时大大降低了谱聚类的空间复杂度。
|
Download:
|
| 图 1 不同聚类类别数时K-means聚类效果示意图 Fig. 1 Schematic diagram of K-means clustering results with different cluster numbers | |
此外,高光谱图像一般包含数十甚至数百个波段,波段间相关性强、冗余度高,且部分波段含有大量噪声信息。因此,需要先对高光谱图像进行降维处理,这样不但可以提高信噪比,而且可以降低处理的时间复杂度。常用的特征降维方法有主成分分析[17](principal component analysis,PCA)、最小噪声分离[18](minimum noise fraction rotation,MNF Rotation)以及快速独立成分分析[19](fast independent component Analysis,FastICA)等,本文在对高光谱图像进行KSC之前采用MNF对数据进行特征降维处理。MNF+KSC方法的主要算法流程如下:
1) 首先采用MNF方法对原始高光谱数据进行特征降维处理。
2) 然后采用K-means方法对原始图像进行粗聚类,聚成C类,得到C个聚类中心点,记为
3) 对于上述聚类中心
4) 然后根据W矩阵分别求得度矩阵D和拉普拉斯矩阵L。
5) 求解拉普拉斯矩阵L的最小特征值对应的特征矢量,进行最终分类。
6) 对应到2)中每个聚类中心对应的原始数据,进行类别标记。
针对上述提出的KSC方法以及MNF+KSC方法,我们使用不同的数据进行实验来验证本文方法良好的聚类性能。
3 实验本文分别使用模拟数据和真实的高光谱图像数据进行聚类实验,通过与K-means算法的聚类结果进行比较,证实本文方法的优势。
3.1 模拟数据本文采用的模拟数据来源为Clustering benchmark datasets[20],最早在2007年ACM TKDD(ACM Transactions on Knowledge Discovery from Data)上的Clustering Aggregation文章中使用,该数据是二维数据,共788个像元,根据欧氏距离划分可分为7类,具体分布如图 2(a)所示,目前该数据被广泛应用于聚类实验[21-22]。对该数据分别采用K-Means算法、谱聚类算法和KSC算法进行聚类实验,结果如下。

|
Download:
|
| 图 2 K-means算法、谱聚类算法以及KSC算法聚类效果对比图 Fig. 2 Clustering result comparison among K-means, spectral clustering, and KSC | |
实验结果表明,对于该模拟数据,K-means算法聚类的结果受初始值选取的影响,且该数据形状分布不规则,所以K-means聚类的效果并不能令人满意,而采用谱聚类方法和KSC方法进行聚类,可以得到较好的聚类效果,该聚类结果初步证实KSC方法的可行性。
3.2 真实高光谱图像数据为进一步验证本文算法的聚类性能,采用两幅真实的高光谱图像进行定量分析实验。采用KSC和MNF+KSC方法对上述2个真实的高光谱数据进行聚类实验,并与K-Means算法的聚类结果进行比较,分别从聚类结果的总体分类精度、Kappa系数以及计算耗时3方面进行比较。本文中实验所用PC机信息如下:Windows 7系统,CPU为Intel Core i5-2430 2.40Hz,内存为4G。
3.2.1 Salinas高光谱数据数据一为覆盖美国加利福尼亚州萨利纳斯(Salinas)地区的AVIRIS数据,数据大小为512×217,空间分辨率为3.7m。AVIRIS共有240个波段,其中波段108~112,154~167,224共20个波段为水吸收波段,在进行聚类处理之前需要去掉这20个波段,剩余204个波段。该高光谱图像包含的地物主要为植被和土壤,一共包含16种不同的地物,其中具体的每种地物样本点数量如表 1所示,该图像地物对应的真值图如图 3所示。
|
|
表 1 Salinas各地物样本信息 Table 1 Detailed information of various samples in Salinas data |

|
Download:
|
| 图 3 Salinas地物真值图 Fig. 3 Ground truth of Salinas data | |
为便于比较,对于K-means、KSC和MNF+KSC方法,我们设置最终的分类类别数均为16。对于KSC和MNF+KSC方法,首先利用K-means对该数据进行粗聚类(人工设置类别数分别为600和300),最终聚类结果如图 4所示,分别计算当粗聚类类别数取600和300时,聚类结果的总体分类精度和Kappa系数,如表 2所示。

|
Download:
|
| 图 4 Salinas数据实验结果对比图(粗聚类类别数为600) Fig. 4 Comparison of clustering results in Salinas data (coarse clustering number is 600) | |
|
|
表 2 Salinas数据聚类精度 Table 2 Accuracies of clustering results in Salinas data |
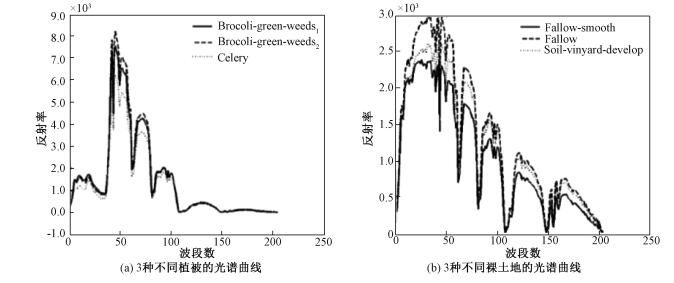
Salinas数据的特点是包含的地物主要为植被和裸地,而它们各自间光谱相似性很高。图 5分别画出3种不同植被和不同裸地的光谱曲线,从中可以看出它们各自之间光谱曲线非常相似,所以Salinas数据所包含的地物相对来说较难区分。对于具有这样特点的数据,当粗聚类类别参数C分别取600和300时,从表 2可以看出KSC与MNF+KSC相对K-Means算法来说,聚类的总体分类精度及Kappa系数均有所提升。而与KSC的计算时间相比,MNF+KSC的计算效率和聚类精度均有所提高。
|
Download:
|
| 图 5 Salinas数据中不同地物的光谱曲线 Fig. 5 Spectra of different objects in Salinas data | |
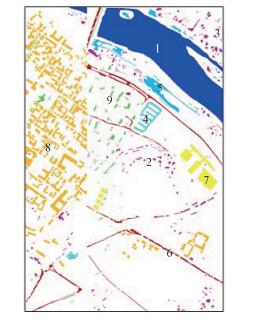
数据二为覆盖意大利北部帕维亚中心(Pavia Center)地区的ROSIS数据,去掉其中的无效数据后图像大小为1096×715,几何分辨率为1.3m,共102个波段。该图像包含的地物有植被、建筑和水体等共9类地物,具体每种植被样本点数量如表 3所示,该图像地物对应的真值图如图 6所示。
|
|
表 3 Pavia Center各地物样本信息 Table 3 Detailed information of various samples in Pavia Center data |
|
Download:
|
| 图 6 Center地物真值图 Fig. 6 Ground truth of Pavia Center data | |
为便于比较,对于K-means算法、KSC算法和MNF+KSC方法,将最终的分类类别数目均设置为9。对于KSC和MNF+KSC方法,首先利用K-means方法对该数据进行粗聚类(人工设置类别数分别为600和300),最终的聚类结果图如图 7所示。计算当粗聚类类别数分别取600和300时,聚类结果的总体分类精度和Kappa系数,如表 4所示。

|
Download:
|
| 图 7 Pavia Center数据实验结果对比图(粗聚类类别数为600) Fig. 7 Comparison of clustering results in Pavia Center data (coarse clustering number is 600) | |
|
|
表 4 Pavia Center数据聚类精度 Table 4 Accuracies of clustering results in Pavia Center data |
Pavia Center数据不同于Salinas数据,其特点是包含的不同地物之间光谱相似性都很低。图 8分别画出3种地物的光谱曲线,从中可以看出它们之间的光谱曲线差异较大,所以Pavia Center数据所包含的地物相对来说较易区分。对具有这样特点的数据,当粗聚类类别参数C分别取600和300时,从表 4可以看出KSC与MNF+KSC相对K-means算法来说,聚类结果的总体分类精度及Kappa系数均有较大幅度提升。而与KSC相比,MNF+KSC的计算效率和聚类精度均有所提高。

|
Download:
|
| 图 8 Pavia Center数据不同地物光谱曲线 Fig. 8 Spectra of different objects in Pavia Center data | |
由以上实验可知,KSC方法与K-means算法比较,聚类精度有所提升。考虑高光谱图像冗余性和信噪比后,采用的MNF+KSC的方法,在降低计算复杂度的同时,聚类精度又在KSC的基础上有较大幅度提升。
4 结束语本文针对谱聚类方法在众多聚类方法中有明显优势但是无法在高光谱图像聚类中直接应用的问题,提出结合K-means的KSC方法,采用K-means首先对高光谱数据进行粗聚类,然后再利用谱聚类方法对上述粗聚类中心做进一步聚类处理,如此使得谱聚类方法在高光谱图像中得以应用。为进一步降低计算复杂度和提高数据信噪比,采用MNF方法对高光谱数据进行特征降维,然后再进行KSC聚类处理。通过对真实高光谱图像数据进行实验,验证了KSC方法和MNF+KSC方法比K-means方法对高光谱图像有更好的聚类性能。
| [1] |
童庆禧. 高光谱遥感[M]. 北京: 高等教育出版社, 2006: 47-65.
|
| [2] |
万余庆. 高光谱遥感应用研究[M]. 北京: 科学出版社, 2006: 35-98.
|
| [3] |
Ma X L, Ren Z Y, Wang Y L. Research on hyperspectral remote sensing image classification based on SAM[J]. System Sciences & Comprehensive Studies in Agriculture, 2009, 25(2): 204-208. |
| [4] |
Shafri H Z M, Suhaili A, Mansor S. The performance of maximum likelihood, spectral angle mapper, neural network and decision tree classifiers in hyperspectral image analysis[J]. Journal of Computer Science, 2007, 3(6): 419-423. DOI:10.3844/jcssp.2007.419.423 |
| [5] |
Gao L, Li J, Khodadadzadeh M, et al. Subspace-based support vector machines for hyperspectral image classifica-tion[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(2): 349-353. |
| [6] |
Hu W, Huang Y, Wei L, et al. Deep convolutional neural networks for hyperspectral image classification[J]. Journal of Sensors, 2015(2): 1-12. |
| [7] |
Han J, Kamber M. Data mining concepts and technique[M]. San Fransisco: Morgan Kaufmann press, 2001: 23-106.
|
| [8] |
Macqueen J. Some methods for classification and analysis of MultiVariate observations[C]//Proc of Berkeley Symposium on Mathematical Statistic-sand Probability, 1967: 281-297.
|
| [9] |
Wagstaff K, Cardie C, Rogers S, et al. Constrained K-means clustering with background knowledge[C]//Eighteenth International Conference on Machine Learning. San Francisco: Morgan Kaufmann Press, 2001: 577-584.
|
| [10] |
Comaniciu D, Meer P. Mean shift:a robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(5): 603-619. |
| [11] |
Ball G H, Hall D J. ISODATA, a novel method of data analysis and pattern classification[R]. Stanford research inst Menlo Park CA, 1965.
|
| [12] |
Ester M, Kriegel H P, Xu X. A densitybased algorithm for discovering clusters a density-based algorithm for discovering clusters in large spatial databases with noise[C]//International Conference on Knowledge Discovery and Data Mining. Portland: AAAI Press, 1996: 226-231.
|
| [13] |
蔡晓妍, 戴冠中, 杨黎斌. 谱聚类算法综述[J]. 计算机科学, 2008, 35(7): 14-18. DOI:10.3969/j.issn.1002-137X.2008.07.004 |
| [14] |
Ng A Y, Jordan M I, Weiss Y. On spectral clustering:analysis and an algorithm[J]. Proc Nips, 2001, 14: 849-856. |
| [15] |
Zelnik-Manor L. Self-tuning spectral clustering[J]. Advances in Neural Information Processing Systems, 2004, 17: 1601-1608. |
| [16] |
Hagen L, Kahng A B. New spectral methods for ratio cut partitioning and clustering[J]. IEEE Transactions on Com-puter-Aided Design of Integrated Circuits and Systems, 1992, 11(9): 1074-1085. DOI:10.1109/43.159993 |
| [17] |
Abdi H, Williams L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(4): 433-459. DOI:10.1002/wics.101 |
| [18] |
Green A, Berman M, Switzer P, et al. A transformation for ordering multispectral data in terms of image quality with implications for noise removal[J]. IEEE Transactions on Geoscience & Remote Sensing, 1988, 26(1): 65-74. |
| [19] |
Chen L J, Zou X J, Chen B B, et al. An improved FastICA algorithm and its application in image feature extraction[J]. Advanced Materials Research, 2011, 204-210: 1485-1489. DOI:10.4028/www.scientific.net/AMR.204-210 |
| [20] |
Pudn.com.Clustering datasets: China[EB/OL]. (2015-04-18)[2018-01-03]. http://www.pudn.com/Download/item/id/2741142.html.
|
| [21] |
Tsaparas P, Mannila H, Gionis A. Clustering aggregation[J]. Acm Transactions on Knowledge Discovery from Data, 2007, 1(1): 4. |
| [22] |
李翔.高光谱影像的聚类分析及应用[D].北京: 北京交通大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015594115.htm
|
 2019, Vol. 36
2019, Vol. 36 


