2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar, SAR)图像配准是图像融合、地物分类、三维重构以及地图修正等工作的基础,近年来国内外学者一直在不断进行研究和探索。目前,SAR图像配准技术根据配准要素的不同可以分为基于灰度的方法、基于变换域的方法和基于特征的方法[1-2]。基于灰度的方法利用图像的灰度信息对图像的相似程度进行度量,该方法实现简单,易于操作,但其应用范围较窄,计算量较大[3];基于变换域的方法通常以傅里叶变换或者小波变换为基础,进行频域或小波域内的配准,该方法对于图像幅度存在微小平移、旋转和缩放时效果较好,其运算速度快,易于硬件实现,并且具有一定程度的抗噪性[4-5];基于特征的方法是遥感图像配准中应用最多的配准方法,该方法不受灰度的影响,通过提取点特征、线特征或者面特征对图像进行匹配,鲁棒性强,匹配效果好[6-8]。其中,尺度不变特征变换(scale invariant feature transform, SIFT)算子是目前公认的最为稳定的特征匹配算子。但是,该算子由于使用高斯差分(difference of Gaussian, DoG)算子,因而具有很强的边缘响应,虽然在算法中采用主曲率的方法进行边缘点剔除,但检测出的特征点中仍存在边缘响应点残留。针对上述问题以及SAR图像存在阴影和斑点噪声等问题,本文通过增加边缘检测和剔除、阴影检测和剔除以及预处理等模块对SIFT算法进行改进。通过多次实验验证,该算法能够提升配准的准确度。借助该算法,本文对同一区域的多幅SAR图像进行配准和非相干叠加融合,可有效提升SAR图像的等效视数,抑制相干斑噪声。
1 SIFT算法简介SIFT算法是Lowe教授提出并完善的图像特征点检测和描述算法[9-11]。该算法在图像发生平移、旋转以及尺度变换时仍然具有较好的鲁棒性,且对噪声也具有一定的稳定性,其主要流程可以分为:尺度空间的构建、特征点的检测和描述、特征点的匹配。
实现尺度变换的唯一线性核是高斯尺度核,因此可以用原始图像与一个可变尺度二维高斯函数的卷积运算定义图像的尺度空间:
| $ L\left( {x,y,\sigma } \right) = G\left( {x,y,k\sigma } \right) * I\left( {x,y} \right), $ | (1) |
式中:
| $ \begin{array}{*{20}{c}} {D\left( {x,y,\sigma } \right) = \left( {G\left( {x,y,k\sigma } \right) - G\left( {x,y,\sigma } \right)} \right) * I\left( {x,y} \right)}\\ { = L\left( {x,y,k\sigma } \right) - L\left( {x,y,\sigma } \right).} \end{array} $ | (2) |
故采用相应的降采样方法与尺度空间相结合构建图像的高斯差分金字塔结构。在进行特征点检测时,每个检测点必须与相邻的所有点,即其本层的8邻域点以及上下两层各9个像素点共26个点比较,以保证检测出的特征点的准确性。对检测到的特征点,统计邻域梯度方向直方图,确定其主方向。需要注意的是,有些特征点除主方向外,还存在辅方向,它对于后续匹配的稳定性至关重要。
特征点的描述是在特征点周围取16像素×16像素的区域,然后将该区域划分为多个4像素×4像素的区域,在每个区域内计算8方向梯度方向直方图,得到128维特征描述子。最后,将描述子向量门限化和规范化,从而改善图像灰度值整体漂移的情况。得到图像的特征向量后,采用欧氏距离对两幅图像进行特征点匹配,当距离小于预设的阈值时就将其作为匹配特征点。
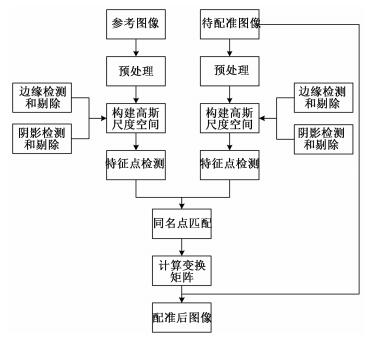
2 基于边缘检测和阴影检测的改进SIFT算法通过多次实验可以发现,将SIFT算法直接应用到SAR图像中检测出的特征点数量有限,并且质量不好,错误匹配情况出现概率很高。为解决这个问题,本文提出基于边缘检测和阴影检测的改进SIFT算法。算法的流程图如图 1所示,首先对SAR图像进行相干斑抑制和图像增强预处理,在构造高斯尺度空间时对边缘和阴影进行检测并剔除,然后对特征点检测和描述,最后同名点进行匹配并计算变换矩阵对待配准图像进行几何变换得到配准后图像。
|
Download:
|
| 图 1 算法流程图 Fig. 1 Flow chart of the algorithm | |
由于SAR系统固有的成像模式,相干斑噪声总是伴随着图像的形成而产生,这些斑点噪声会干扰图像中特征点的检测,降低特征点检测的准确性,进而影响到SAR图像配准的效果。本文采用增强Lee滤波[12]对SAR图像进行平滑处理,Lee滤波的基本思想是利用图像局部统计特性控制滤波器的输出,使滤波器自适应于图像的变化。增强Lee滤波算法在SAR图像均匀区域采用均值滤波进行平滑处理;在不均匀区域采用Lee滤波进行平滑处理,保持图像的细节信息;在包含分离点目标的区域不进行任何平滑处理,因此,增强Lee滤波算法在平滑SAR图像时还具有一定的细节保持能力。
SAR图像的灰度分布集中在较窄的范围内,为展宽灰度,突出图像特征,需要对图像进行增强处理。本文采用直方图均衡化对图像进行增强处理,SAR图像在经过直方图均衡化后,图像对比度变大,灰度分布变得更加均衡,而在原图像中难以分辨的细节信息也有了一定的加强。
2.2 边缘检测和剔除在构建高斯尺度空间时,SIFT算法使用DoG算子,其边缘响应会严重地影响SAR图像配准算法的准确性,如果不消除这种响应,采用该算法检测到的特征点在SAR图像边缘处分布较多,并且这些点的存在都是近邻的,这样会造成一定程度的失配、错配现象。在SIFT算法中采用主曲率的方法检测边缘响应点并剔除。表 1列出部分实验结果,对其进行分析可知,主曲率方法仅可去除一部分边缘响应点,SIFT算法检测出的特征点中仍然含有较多的边缘响应点。
|
|
表 1 SIFT特征点与边缘点数量对比 Table 1 Comparison of the numbers of SIFT feature points and edge points |
针对主曲率方法不能将检测到的特征点中边缘响应点完全消除的问题,本文首先采用指数加权均值比(ratio Of exponentially weighted averages, ROEWA)算子[13-14]对SAR图像的边缘区域进行检测并剔除。ROEWA算子是由Fjrtoft提出的一种适用于SAR图像的边缘检测算子。该算子使用在多边缘模型基础上设计的一种基于最小均方误差的指数平滑滤波器进行均值估计,使用该滤波器计算得到的均值是根据一定权值计算出来的均值。在离散的情形下,可以通过一个因果滤波器f1(x)和一个非因果滤波器f2(x)来实现该滤波器,此时该滤波器可表示为
| $ \begin{array}{*{20}{c}} {f\left( x \right) = \frac{1}{{1 + b}}{f_1}\left( x \right) + \frac{b}{{1 + b}}{f_2}\left( {x - 1} \right),}\\ {x = 1,2, \cdots ,N.} \end{array} $ | (3) |
式中:0 < b=e-α < 1;α为滤波系数。而f1(x)和f2(x)经过推导可以表示为:
| $ {f_1}\left( x \right) = a{e_1}\left( x \right) + b{f_1}\left( {x - 1} \right),x = 1,2, \cdots ,N, $ | (4) |
| $ {f_2}\left( x \right) = a{e_2}\left( x \right) + b{f_2}\left( {x + 1} \right),x = N,N - 1, \cdots ,1. $ | (5) |
式中:e1(x)和e2(x)为滤波器的输入信号;b=e-α;a=1-b。
该滤波器又被称为无限对称指数滤波器,可以将其扩展到二维空间,表达式如下
| $ {f_{{\rm{2d}}}}\left( {x,y} \right) = f\left( x \right)f\left( y \right). $ | (6) |
在计算水平方向边缘强度分量时,采用一维平滑滤波器f(y)对图像的每一列进行滤波,再利用因果滤波器f1(x)和非因果滤波器f2(x)对每一行进行滤波,这样便可以获得水平方向边缘强度因果和非因果指数加权均值:
| $ {\mu _{{X_1}}} = {f_1}\left( x \right) * \left[ {f\left( y \right) \otimes I\left( {x,y} \right)} \right], $ | (7) |
| $ {\mu _{{X_2}}} = {f_2}\left( x \right) * \left[ {f\left( y \right) \otimes I\left( {x,y} \right)} \right]. $ | (8) |
式中:
| $ \begin{array}{l} {s_1}\left( x \right) = a\left[ {{e_1}\left( x \right) - {s_1}\left( {x - 1} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;{s_1}\left( {x - 1} \right),x = 1,2, \cdots ,N, \end{array} $ | (9) |
| $ \begin{array}{l} {s_2}\left( x \right) = a\left[ {{e_2}\left( x \right) - {s_2}\left( {x + 1} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;{s_2}\left( {x + 1} \right),x = N,N - 1, \cdots ,1. \end{array} $ | (10) |
X方向和Y方向的4种指数加权均值都可以由式(7)~式(10)与(3)式联立求得。这样,水平方向的边缘强度分量可以得到
| $ {R_{{X_{\max }}}}\left( {x,y} \right) = \max \left\{ {\frac{{{\mu _{{X_1}}}\left( {x - 1,y} \right)}}{{{\mu _{{X_2}}}\left( {x + 1,y} \right)}},\frac{{{\mu _{{X_2}}}\left( {x + 1,y} \right)}}{{{\mu _{{X_1}}}\left( {x - 1,y} \right)}}} \right\}. $ | (11) |
同理,可以得到垂直方向的边缘强度分量,在得到水平和垂直方向的边缘强度分量之后,通过简单地运算就可以得到最终的边缘强度为
| $ {R_{\max }}\left( {x,y} \right) = \sqrt {R_{{X_{\max }}}^2\left( {x,y} \right) + R_{{Y_{\max }}}^2\left( {x,y} \right)} . $ | (12) |
采用ROEWA算子对SAR图像进行边缘检测的效果如图 2所示,其中,黑色部分代表边缘区域,白色部分代表非边缘区域。SIFT算法需要构建高斯差分金字塔,该过程可以分为图像高斯平滑、图像降采样以及同组图像相邻层相减3部分完成。为了将边缘检测图像融入该过程,对边缘检测得到的图像进行降采样处理。

|
Download:
|
| 图 2 边缘检测效果 Fig. 2 Edge detection results | |
值得注意的是,本文算法在进行边缘检测和剔除时,并没有对检测到的边缘进行细化处理。如果对边缘进行细化的话,为保证彻底消除边缘响应的影响,在剔除边缘的同时需要检测边缘的邻域并进行剔除操作,这样不仅在边缘细化时会耗费大量的时间,而且在边缘邻域检测时也会耗费一定的时间,极大地降低算法的效率。而且在使用SIFT算法检测特征点时能够得到足够的特征点,因此剔除未经细化处理的边缘不会对算法产生显著的影响。
2.3 阴影检测和剔除在对SAR图像进行配准时,由于在不同图像中,阴影区域的大小、形状以及方向会随着入射角度以及照射方向的不同等发生改变,从而直接影响SAR图像配准的精度。因此,为降低阴影对配准精度的影响,改进算法对SAR图像阴影区域通过最大类间方差法[15-16](OTSU)进行检测并剔除。最大类间方差法能够自适应地确定阈值,将SAR图像分为前景区域和背景区域两部分。
| $ g = {\omega _0}{\omega _1}{\left( {{\mu _0} - {\mu _1}} \right)^2}. $ | (13) |
式(13)就是类间方差的表达式。式中:ω0表示前景区域占整幅图像的比例,μ0表示其平均灰度,ω1表示背景区域占整幅图像的比例,μ1表示其平均灰度。遍历整个灰度级,找到使类间方差最大的灰度值,即为阴影分割所需阈值T。在遍历时多次重新计算前景、背景占比及其平均灰度,会耗费大量的时间,因此,本文采用前一阈值下的计算结果迭代计算新阈值下的结果。
| $ N_0^{\left( {T + 1} \right)} = N_0^{\left( T \right)} + {G_{T + 1}}, $ | (14) |
| $ \omega _0^{\left( {T + 1} \right)} = \frac{{N_0^{\left( {T + 1} \right)}}}{N}, $ | (15) |
| $ {\rm{SUM}}_0^{\left( {T + 1} \right)} = {\rm{SUM}}_0^{\left( T \right)} + \left( {T + 1} \right) \cdot {G_{T + 1}}, $ | (16) |
| $ \mu _0^{\left( {T + 1} \right)} = \frac{{{\rm{SUM}}_0^{\left( {T + 1} \right)}}}{{N_0^{\left( {T + 1} \right)}}}, $ | (17) |
| $ g = \omega _0^{\left( {T + 1} \right)}\omega _1^{\left( {T + 1} \right)}{\left( {\mu _0^{\left( {T + 1} \right)} - \mu _1^{\left( {T + 1} \right)}} \right)^2}. $ | (18) |
式中:N0表示前景区域的像素个数,N表示整幅图像总像素个数,SUM0表示前景区域像素总灰度值,μ0表示前景区域平均灰度值,GT+1表示灰度为T+1的像素个数,T是从0到254的灰度值。上述表达式迭代求出前景占比及其平均灰度,同理,背景占比及其平均灰度也可迭代求解,遍历整个灰度级得出类间方差的结果,当使得g最大时,T+1就是进行阴影分割时所需阈值。在一定程度上,该方式能够节省运算时间,提升算法效率。
使用改进的最大类间方差法对SAR图像进行阴影检测的效果如图 3(b)所示,其中,黑色部分代表阴影区域,白色部分代表非阴影区域。但是使用OTSU算法得出的分割结果中含有伪阴影点和伪非阴影点,同时在阴影区域和非阴影区域内部还存在断裂结构和空洞,可以通过形态学闭运算改善分割效果,连接断裂结构,形成较大连通区域,形态学处理结果如图 3(c)所示。

|
Download:
|
| 图 3 阴影检测效果 Fig. 3 Shadow detection results | |
得到阴影检测图像之后,同样对其进行降采样处理,然后与边缘检测降采样处理结果一起融入到尺度空间的构建过程中。在特征点检测之前首先判断待检测像素点是否属于边缘区域或阴影区域,如果判断该点属于此区域,则将该点舍弃,不对该点进行检测;相反,如果判断该点不属于此区域,则保留该点并继续判断该点是否为极值点,值得注意的是,在确定极值点时,要使用未经边缘和阴影剔除的尺度空间进行判断。遍历整个空间,得到特征点集,为后续配准工作奠定基础。
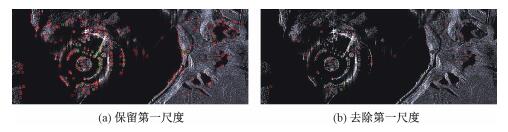
2.4 跳过第一尺度检测使用SIFT算法对SAR图像多次进行特征点检测实验,部分实验结果如图 4和表 2所示,其中,绿色圆圈表示最终被认定为匹配点的特征点,而红色圆圈表示最终未被认定为匹配点的特征点。对比实验结果可以发现,在高斯金字塔第一尺度空间进行检测时,虽然能够检测出大量的特征点,但是其中匹配点所占比例不高,在后续的处理工作中,该尺度空间检测到的特征点即使被认定为匹配点,也存在很大比例的错误匹配点。而且在SAR图像中存在着不可避免的相干斑噪声,在构建尺度空间时,采用高斯级联滤波器,所以尺度越大,噪声被滤除的效果越明显。因此,去掉第一尺度空间进行检测虽然使检测出的特征点数量减少,但基本上不会影响正确匹配点的数量,反而能够提高正确匹配点的比例,降低相干斑噪声的影响,同时减少特征点检测的耗时。
|
Download:
|
| 图 4 特征点检测效果 Fig. 4 Detection results of feature points | |
|
|
表 2 特征点检测效果对比 Table 2 Comparison of feature point detection results |
完成特征点检测之后,使用128维特征描述子对特征点进行描述,然后以欧氏距离作为其相似性度量,利用KD树的数据结构搜索最近邻点和次近邻点,再使用随机抽样一致(random sample consensus, RANSAC)算法剔除错误匹配点,从而生成同名特征点对。考虑到配准效果与算法效率的平衡,采用仿射变换模型[17]对待配准图像进行几何校正。其变换模型如下
| $ \left[ {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{t_x}}\\ {{a_3}}&{{a_4}}&{{t_y}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right]. $ | (19) |
将得到的同名特征点对代入仿射变换模型中,求得仿射变换矩阵,再将待配准图像代入上式进行变换完成几何校正,得出配准后图像。
3 实验结果与分析本文所选用的实验数据为中国科学院电子学研究所实测的多组SAR图像,采用SIFT算法与改进SIFT算法分别对其进行实验,图 5所示为其中两组图像使用在同一参数下的两种算法进行特征点检测和匹配的结果。

|
Download:
|
| 图 5 特征点匹配对比效果 Fig. 5 Comparison of feature point matching results | |
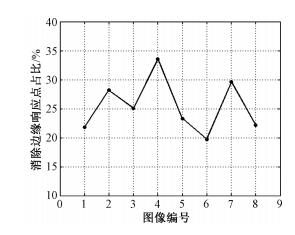
改进SIFT算法消除边缘响应点占总特征点的比例如图 6所示,其中,横坐标为图像编号,纵坐标为消除的边缘响应点占比。可以发现,改进SIFT算法能够消除25%左右的边缘响应点,使算法检测出的特征点更加稳定,利于后续配准工作的进行。
|
Download:
|
| 图 6 消除边缘响应点占比 Fig. 6 Proportion of eliminated edge response points | |
对特征点匹配结果通过匹配对数、正确匹配对数、匹配正确率、空间分布质量、均方根误差以及执行时间进行评价,其结果如表 3所示。其中,空间分布质量表征算法检测出的特征点分布的分散程度,其计算公式如下
| $ {\rm{DQ}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} + \sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} }}{n}} /\left( {M + N} \right). $ | (20) |
|
|
表 3 特征点匹配评价结果 Table 3 Evaluation results of feature point matching |
式中:xi和yi分别表示特征点所在坐标,而
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^M {\sum\limits_{i = 1}^N {{{\left( {R\left( {i,j} \right) - F\left( {i,j} \right)} \right)}^2}} } }}{{M \cdot N}}} . $ | (21) |
式中:R和F分别为配准前后的图像灰度值,M和N则为图像的高度和宽度。
将改进算法应用于SAR图像配准,其中,第1组图像的像素分别为793×321和669×301,匹配对数量由20对增加到59对,正确匹配率由55%提升至98%,第2组图像的像素分别为450×287和424×246,匹配对数量由53对增加到197对,正确匹配率由74%提升至99%,且两组图像的RMSE减小,空间分布质量增大。该实验结果表明,两种算法相比,在同一参数下,改进算法能够大幅度提高匹配对数量和匹配的正确率,而且空间分布质量较改进之前也有大幅度的提升,配准精度也随之提高。由于增加了预处理、边缘检测和剔除以及阴影检测和剔除等3个模块,对算法进行分析并且对比表 3执行时间可知,改进算法的时间复杂度与SIFT算法仍在同一个量级上,但有所增加,所以实时性效果并不是特别理想。
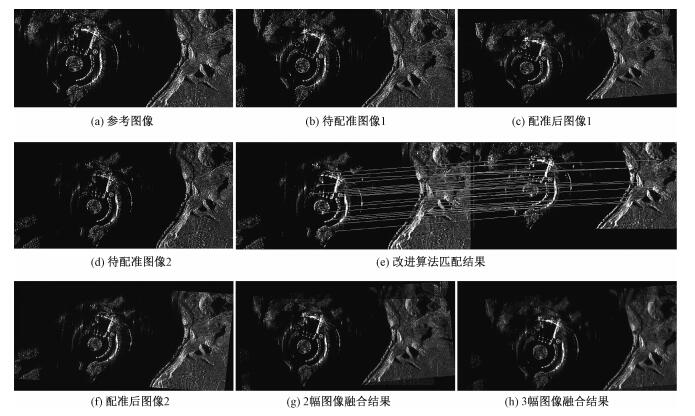
将第1组SAR图像进行配准最终的结果如图 7所示。其中,图 7(a)是参考图像,图 7(b)是待配准图像1,图 7(c)是待配准图像1配准之后的结果,图 7(g)是将参考图像和配准后图像1进行非相干叠加融合之后的结果。
|
Download:
|
| 图 7 图像配准和融合结果 Fig. 7 Image registration and fusion results | |
借助于本文算法,在参考图像指定的前提下,还可以对多幅SAR图像进行配准,图 7(d)是待配准图像2,图 7(e)是待配准图像2与参考图像检测出的特征点的匹配结果,图 7(f)是待配准图像2以图 7(a)作为参考图像配准之后的结果,图 7(h)是将3幅图像进行非相干叠加融合的结果。对非相干叠加融合图像采用等效视数作为评价指标进行评价的结果如表 4所示,通过对比可以发现,将图像配准后非相干叠加,图像的等效视数增大,类似于多视处理的效果,而且在叠加后其等效视数接近于理论值,进一步印证了改进SIFT算法的配准精度。
|
|
表 4 图像非相干叠加评价结果 Table 4 Evaluation results of image incoherent superposition |
本文算法是在SIFT算法基础上,针对SAR图像的特点进行相应预处理并将边缘检测与阴影检测融合到算法中,提高算法的配准精度和稳定性,使算法能够更好地适用于SAR图像的配准工作,为后续图像融合、地物分类、三维重建以及地图修正等工作提供了很好的基础。但该算法仅适用于多幅SAR图像之间的配准,对光学图像与SAR图像之间的配准有待进一步研究。
| [1] |
李孚煜, 叶发茂. 基于SIFT的遥感图像配准技术综述[J]. 国土资源遥感, 2016, 28(2): 14-20. |
| [2] |
徐颖, 周焰. SAR图像配准方法综述[J]. 地理空间信息, 2013, 11(3): 63-66. DOI:10.11709/j.issn.1672-4623.2013.03.023 |
| [3] |
Chatelain F, Tourneret J Y, Inglada J, et al. Bivariate gamma distributions for image registration and change detection[J]. IEEE Transactions on Image Processing, 2007, 16(7): 1796. DOI:10.1109/TIP.2007.896651 |
| [4] |
Argyriou V, Tzimiropoulos G. Frequency domain subpixel registration usingHOG phase correlation[J]. Computer Vision & Image Understanding, 2016, 155: 70-82. |
| [5] |
Suo Z, Li Z, Bao Z. Multi-channel SAR-GMTI method robust to Coregistration Error of SAR Images[J]. Aerospace & Electronic Systems IEEE Transactions on, 2010, 46(4): 2035-2043. |
| [6] |
阿布来提·依布拉音, 王治强, 刘薇, 高慧婷. 基于Hough直线检测的深度图像配准方法[J]. 中国科学院研究生院学报, 2013, 30(1): 112-116. |
| [7] |
Suri S, Reinartz P. Mutual-information-based registration of TerraSAR-X and ikonos imagery in urban areas[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 48(2): 939-949. |
| [8] |
苏娟, 李彬, 王延钊. 一种基于封闭均匀区域的SAR图像配准方法[J]. 电子与信息学报, 2016, 38(12): 3282-3288. |
| [9] |
Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [10] |
Hossein-Nejad Z, Nasri M. An adaptive image registration method based on SIFT features and RANSAC transform[J]. Computers & Electrical Engineering, 2016, 62: 524-537. |
| [11] |
王茜, 宁纪锋, 曹宇翔, 等. 基于SIFT算法的无人机遥感图像拼接技术[J]. 吉林大学学报(信息科学版), 2017, 35(2): 188-197. DOI:10.3969/j.issn.1671-5896.2017.02.013 |
| [12] |
Zhong H, Zhang J, Liu G. Robust polarimetric SAR despeckling based on nonlocal means and distributed Lee filter[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(7): 4198-4210. |
| [13] |
Fjørtoft R, Lopès A, Marthon P, et al. An optimal multiedge detector for SAR image segmentation[J]. IEEE Transactions on Geoscience & Remote Sensing, 1998, 36(3): 793-802. |
| [14] |
刘夯, 何政伟, 赵银兵, 等. SAR图像ROEWA边缘检测器的改进[J]. 遥感学报, 2017, 21(2): 273-279. |
| [15] |
Bangare S L, Dubal A, Bangare P S, et al. Reviewing Otsu's method for image thresholding[J]. International Journal of Applied Engineering Research, 2015, 10(9): 21777-21783. |
| [16] |
赵夫群, 周明全, 耿国华, 等. 基于GA-Otsu法的图像阈值分割及定量识别[J]. 吉林大学学报(工学版), 2017, 47(3): 959-964. |
| [17] |
Liu X, Tian Z, Lu Q, et al. A new affine invariant descriptor framework in shearlets domain for SAR image multiscale registration[J]. AEU-International Journal of Electronics and Communications, 2013, 67(9): 743-753. DOI:10.1016/j.aeue.2013.03.002 |
 2019, Vol. 36
2019, Vol. 36 


