2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
时间序列InSAR技术[1-2],可以对区域和人工建筑进行长时间观测,以较低的成本,获取区域和建筑大面积、高精度的微小形变信息,在地理测量领域有着广泛应用。而且目前由于高分辨率SAR影像的使用,时间序列InSAR技术甚至可以对单个具体建筑进行形变分析。相比于传统测量手段,这种空间遥感技术有许多优点,在桥梁形变检测领域有着广阔的应用前景,对桥梁安全监测有着重大意义。但目前在行业内,大型斜拉桥的时间序列InSAR形变检测仍然面临较大困难,现有处理算法无法获取正确的大型桥梁形变结果,极大地限制了时间序列InSAR技术在桥梁领域的应用。
本文以洞庭湖大桥为例,深入分析目前时间序列InSAR处理方法在大型斜拉桥上遇到的问题,证明该问题主要产生于相位解缠过程。由于大桥所在区域残差点分布比较复杂,目前常规的稀疏网络MCF相位解缠方法[3-7]在桥塔附近的残差点会产生错误的连接,导致该区域产生的枝切线会穿过桥面,带来较大的解缠误差。因此,本文提出一种新的相位解缠方法,首先构建Delaunay约束三角网络,减少残差点数目;然后为避免出现较长的枝切线,同时阻止枝切线穿过桥面,对残差点按距离进行聚类,从而将区域分成若干个残差点聚集区;最后对每块中的正负残差点进行连接,为平衡孤立残差点,引入一部分接地点作为虚拟残差点,采用二分图最优权匹配方法,对正负残差点以及接地点进行最优匹配连接,极大地降低了枝切线的长度;最后利用路径积分方法得到正确的解缠相位。通过在洞庭湖大桥实际星载SAR数据上进行实验验证,并与MCF算法解缠结果进行对比,证明该算法有效改善了解缠结果,减少了解缠误差,适合于桥梁线状区域的相位解缠。
1 稀疏网络MCF相位解缠基于永久散射体的干涉(PSI)技术,是目前时间序列InSAR技术最为常用的处理方法,其通过对干涉图中的高相干性点(PS)进行分析,经过干涉处理、相位解缠和形变解算操作,可以获取这些PS点的形变结果,从而得到整个区域的形变信息。
由于PSI技术只对PS点进行处理,并且PS点在干涉图中是稀疏分布,而MCF相位解缠方法是基于网络的方法,必须先对PS点构建网络,一般使用Delaunay三角化方法来构建稀疏网络。因此基于Delaunay稀疏三角网络的MCF算法是PSI技术中使用最多的相位解缠方法,该算法成熟可靠,计算效率高,在各类商用软件中也广泛使用,下面简单介绍该算法原理与步骤。
1.1 基于Delaunay稀疏三角网络的MCF算法定义缠绕相位梯度ϕij,解缠相位梯度ϕij,需要补偿的相位整数模糊数kij, 即有
| $ {\phi _{ij}} = {\phi _{ij}} + 2{\rm{ \mathsf{ π} }}{k_{ij}}. $ | (1) |
相位解缠过程也就是求kij,在MCF相位解缠算法中,kij表示每条边上的网络流大小,如图 1所示。

|
Download:
|
| 图 1 网络流算法模型 Fig. 1 Network flow algorithm model | |
MCF算法通过把正负残差点视作供给点和需求点,将残差点的连接问题,转换成网络流问题,在构建的Delaunay稀疏三角网络中,采用L1范数优化模型,使得总的补偿数最小。
| $ {\rm{min}}\sum\limits_{ij} {} |{c_{ij}}{k_{ij}}|. $ | (2) |
若采用有向图模型,可将公式(2)转换成线性约束形式,本质上来说,该约束等效于要求在一定加权条件下使得总的枝切线长度最小,而MCF方法就利用最小费用流算法求得最优加权枝切线。
该算法的具体步骤:首先对PS点构建Delaunay三角网络;然后对每个三角形,根据闭合路径相位梯度积分是否为0,识别正负残差点;再采用最小费用流算法,得到正负残差点对的最优连接方式,确定枝切线位置;最后采用flood-fill方法,选择合适的参考点,对缠绕相位梯度沿路径积分,当积分路径经过枝切线时,要根据枝切线上流的大小,对积分相位进行补偿2π的整数倍操作,最终获得解缠相位图。
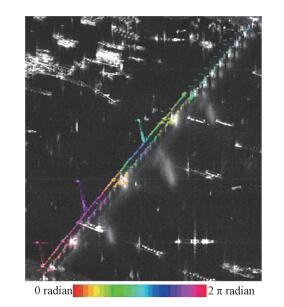
1.2 实验结果本文实验数据采用2016年上半年共17幅洞庭湖大桥区域的TerraSAR聚束模式影像,从17幅影像的两两干涉对中挑选出56幅相干性比较好的干涉对,根据PSI处理方法进行形变分析,采用幅度离差法和谱相关系数法选出的桥上PS点,并对PS点相位进行干涉处理,得到桥面PS点的差分干涉相位图,取某幅干涉图如图 2所示(颜色变化表示干涉相位值变化)。
|
Download:
|
| 图 2 洞庭湖大桥某差分干涉相位图 Fig. 2 The difference interferometry phase image of the Dongtinghu Bridge | |
虽然在PSI处理流程中,可以先对差分干涉相位进行形变解算,然后再进行相位解缠,但由于斜拉桥受到较大的热形变和负载影响,带来极大的桥面PS点形变相位变化,此时,若直接采用形变解算算法会遇到较大困难,甚至无法求解形变结果。因此,为正确进行形变分析,必须先对桥面相位进行相位解缠,然后对解缠相位进行形变解算。根据1.1节中的MCF相位解缠算法步骤,对洞庭湖大桥区域差分干涉相位进行相位解缠,得到如图 3所示的结果,其中图 3(d)为了分析解缠相位误差,没有给出解缠相位干涉图,而是给出解缠相位在空间分布的情况,可以更为直观地发现误差问题。
|
Download:
|
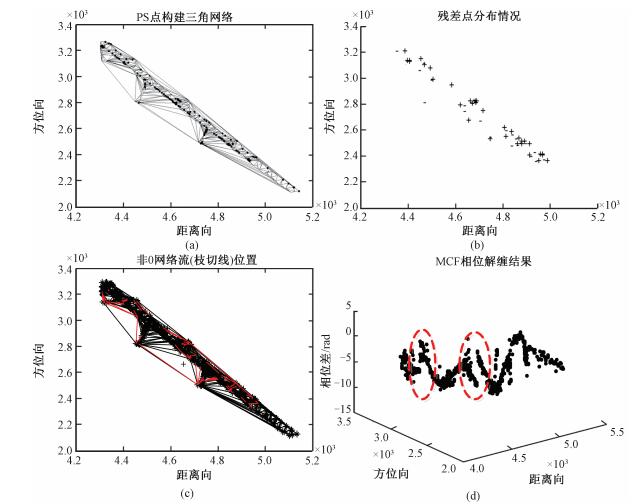
| 图 3 洞庭湖大桥稀疏三角网络MCF相位解缠结果 Fig. 3 The phase unwrapped results of the Dongtinghu Bridge by sparse Delaunay triangulation MCF method | |
从图 3(a)可看到,利用Delaunay三角化方法构建的三角网络存在一些很长的边,而且这些边的位置都在水面上,显然这些边是不合理的,很可能会出现相位梯度变化太大的问题,导致相位解缠出错;图 3(b)为某干涉对相位利用闭合相位梯度积分是否为0,识别出的残差点,正负残差点分别用“+”和“-”表示,可发现三角网络中较长的边会带来许多残差点;图 3(c)为利用MCF得到的非零网络流(枝切线)结果,用红色标注;图 3(d)为利用路径积分方法,选择桥面第一个点为参考点,对缠绕相位梯度积分的解缠相位。由于从干涉图上难以直观地发现解缠误差,因此给出的是桥面PS点解缠相位在空间上分布结果,可看到解缠相位中红圈所示区域出现明显的跳变不连续情况,反映的正是MCF相位解缠过程中存在解缠误差。在56对解缠相位结果中,仅有4对相位变化较小的干涉图解缠结果是正确的,其余解缠相位均存在大量跳变误差。这样,在后续对解缠相位进行形变解算时,这些相位跳变点给形变解算过程带来较大困难,导致出现错误的形变结果。
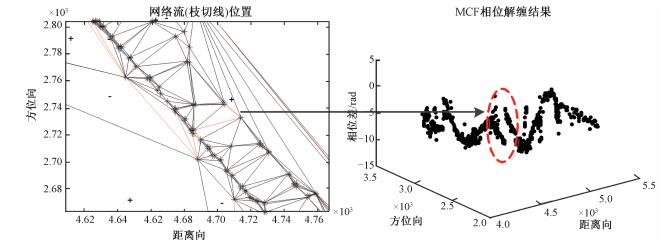
对正负残差点的连接方式进行分析,可发现一旦有连接正负残差点的枝切线穿过桥面,就会导致解缠相位出现误差,枝切线和解缠误差对应关系如图 4所示。出现这种情况的主要原因在于,斜拉桥桥塔区域对桥面产生遮挡,在桥塔附近,桥面的点与桥塔点混在一起,而桥塔点本身存在较大的高程相位变化,在该区域极易出现孤立残差点,导致正负残差点出现不合理的连接,带来解缠误差;另外,桥梁区域为线状区域,一旦某点出现解缠误差,会导致误差传播到整个桥上,因此只要桥面存在不合理的枝切线,就会带来较大的解缠误差,并导致桥面的形变结果无法正确获取,这也是MCF算法在桥梁区域解缠结果不如城区的原因。
|
Download:
|
| 图 4 枝切线位置和解缠误差对应关系 Fig. 4 Relationship between branch cut locations and phase unwrapped errors | |
从洞庭湖大桥的处理结果来看,MCF算法在进行正负残差点连接时,仅仅以加权连接线长短为目的,没有考虑区域具体特征,在斜拉桥桥塔附近的残差点容易产生错误的连接。同理,目前其他的算法[8-18],如枝切法、最小生成树算法等这类路径跟踪算法,还有最优化方法,在处理大型桥梁时都会遇到较大的困难。本文提出一种基于二分图的分块残差点最优匹配算法,可在一定程度上约束残差点的连接,获取正确的解缠结果。
2 基于二分图的分块残差点最优匹配算法 2.1 算法流程基于二分图的分块残差点最优匹配算法主要有3个步骤,构建约束三角网络、残差点分块和残差点二分图最优匹配,下面对这3点分别进行详细介绍。
1) 构建约束三角网络
从桥面PS点构成的Delaunay三角网络可看到,由于Delaunay构网只考虑拓扑结构,保证构建的网络结构满足凸包性质,在桥面上一些凸出部分周围构建的三角形会出现不合理的长边,而这类区域极易产生残差点。因此需要对构建的Delaunay三角网络进行约束,在保证网络连通性的同时,设置一个合理的边长阈值,构建Delaunay约束三角网络。
2) 残差点分块
构建约束三角网络,会在原有的Delaunay三角网络上删除很多三角边,在残差点数目会降低同时,也给正负残差点的匹配带来一些问题,由于桥面的残差点分布变得更加稀疏,很可能会导致许多过长的连接线出现。使用分块方法可以解决该问题,传统上分块操作,主要是按影像数据块大小进行处理的,但由于桥梁所在区域存在一些凸出部分,会给数据分块时带来一些问题。本文采用基于残差点距离的分块方法,对残差点进行聚类,具体操作如下:
① 计算每个残差点到其他残差点的距离,包括欧式距离和连通性距离(即连接两残差点需要经过的最小三角形边数),构建残差点距离矩阵。
② 根据欧氏距离阈值和连通性距离阈值,判断两残差点是否分在同一块,若在,则为1,否则为0,从而构建分块残差点0~1矩阵。
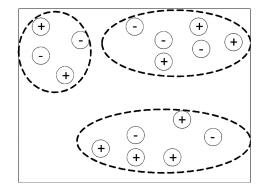
③ 遍历残差点0~1矩阵的各连通分量,其中每个连通分量中的残差点即分在同一块,得到最终残差点的分块结果如图 5所示。
|
Download:
|
| 图 5 残差点分块示意图 Fig. 5 Residual points partition | |
3) 残差点二分图最优匹配
残差点的最优连接属于组合优化问题,选择合适的正负残差点的连接方式,能使得总得枝切线长度最小,枝切线的总长度一般定义如下:
| $ L = \sum\limits_{i = 1}^N {} \sqrt {{{(x_i^ + - x_i^ - )}^2} + {{(y_i^ + - y_i^ - )}^2}} , $ | (3) |
式中:(xi+, yi+),(xi-, yi-)分别为正负残差点的坐标;N为枝切线条数;L为总枝切线长度。
公式(3)只考虑正负残差点完全匹配的情况。实际残差点分块后,为保证每块中正负残差点数目保持平衡,需要适当引入一部分接地点来平衡残差点的极性。若将接地点视作虚拟的正负残差点,与相应的残差点进行匹配,枝切线长度就仍能保持公式(3)中的形式,即N个正残差点与N个负残差点匹配,这样正负残差点的连接可转换成二分图最优匹配模型,如图 6所示。

|
Download:
|
| 图 6 残差点连接的二分图匹配模型 Fig. 6 The bipartite graph matching model for residual points | |
利用KM算法来获取最优匹配结果,假定正残差点个数大于负残差点,算法具体步骤如下:
① 将正残差点构成点集{X},负残差点构成点集{Y};
② 计算每个正残差点到每个负残差点的距离,由于正残差点多,要加入一部分接地点作为虚拟的负残差点,因此需要计算每个正残差点到最近接地点的距离。取所有的这些距离的负值作为正负残差点二分图G(X, Y)的匹配权值矩阵;
③ 定义顶标,正残差点顶标{Cx},负残差点顶标{Cy};
④ 初始化顶标:
| $ \begin{array}{l} {c_x}\left( i \right) = {\rm{max}}\left\{ {G\left( {i, j} \right)} \right\}, j = 1, 2 \ldots N, \\ {c_y}\left( i \right) = 0; \end{array} $ | (4) |
⑤ 使用匈牙利匹配算法求最优匹配;
⑥ 对匹配结果中任意一条匹配边,判断其两端顶点对应的顶标是否满足
| $ {c_x}\left( i \right) + {c_y}\left( j \right) = = G\left( {i, j} \right), $ | (5) |
若相等,则该匹配结果即为最优权匹配,停止迭代,否则继续下一步;
⑦ 对不满足⑥中条件的匹配节点更新顶标:
| $ \begin{array}{l} {c_x}\left( i \right) = {c_x}\left( i \right) - {\rm{min}}\left( {{c_x}\left( i \right) + {c_y}\left( j \right) - G\left( {i, j} \right)} \right), \\ {c_y}\left( j \right) = {c_y}\left( j \right) + {\rm{min}}({c_x}\left( i \right) + {c_y}\left( j \right) - G\left( {i, j} \right)). \end{array} $ | (6) |
⑧ 跳转到步骤⑤,直到算法结束。
该算法时间复杂度为O(N4),但由于采用分块方法对残差点进行了细分,每块中要匹配的残差点数目比较小,因此算法计算效率很高。使用匹配算法得到最优残差点匹配连接后,就可以将相应的残差点连接起来,得到最优枝切线,后续对缠绕相位梯度进行路径积分就能得到解缠相位。
2.2 实验验证1) 约束三角网络
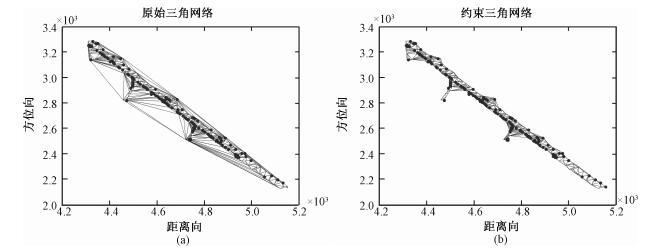
对洞庭湖大桥PS点构建约束三角网络,采用的边长阈值为100,得到的三角网络如图 7所示。
|
Download:
|
| 图 7 (a) 原始三角网络和(b)约束三角网络 Fig. 7 Delaunay triangulation network (a) and the constrained triangulation network (b) | |
从图 7(b)可看到,较长的边都被排除了,剩下的三角形都是比较合理的,都集中在桥上,而不再有边出现在水面上。另外,采用约束三角网络去除不合理边的同时,残差点也极大地减少,平均而言,残差点数目减少约1/5,残差点数目随三角网络变化如表 1所示。
|
|
表 1 三角网络和约束三角网络残差点个数对比 Table 1 Comparison of the residue number between Delaunay triangulation network and the constrained triangulation network |
2) 残差点分块
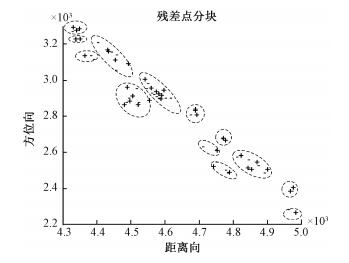
在分块过程中,为避免有正负残差点的连线穿过桥面,需要设置较小的距离阈值,但该距离阈值同时也要足够大,以保证块内的正负残差点能够正常匹配。取洞庭湖大桥某干涉图,对其构建约束三角网络后,对每个三角网,利用闭合相位梯度是否为0,来识别出其中的正负残差点,然后选择好合适的阈值,根据2.1节中的分块算法,对残差点进行分块,得如图 8所示结果。
|
Download:
|
| 图 8 残差点分块结果示例图 Fig. 8 Residual points partition results | |
从图 8可看到,采用分块算法将残差点分成了很多小的聚集区域,但这不会影响块内正负残差点极性的平衡,因为桥梁区域为线状分布的特点,会存在很多边界,有丰富的接地点,通过加入接地点可以平衡多余极性的残差点。对残差点进行分块,可以避免较长的连接线,同时减小进行匹配的正负残差点数目,降低后续匹配优化的难度。
3) 残差点二分图最优匹配
根据前面的KM算法流程,对洞庭湖大桥的某干涉图分块残差点进行匹配,得到枝切线结果和MCF算法对比如图 9所示。

|
Download:
|
| 图 9 MCF算法得到的枝切线分布图(a)和本文算法得到的枝切线分布图(b) Fig. 9 The branch cuts by MCF method (a) and by the proposed method (b) | |
从图 9可看到,本文提出的算法产生枝切线长度比较小,明显优于MCF算法结果。通过采用残差点分块方式,正负残差点在保持MCF算法中较短枝切线的同时,对长枝切线处正负残差点进行重新连接,从而获得整体比较短的枝切线结果。
完成残差点的连接后,就可以选择积分参考点,采用路径积分方法对缠绕相位梯度进行积分,得到解缠相位。按照该方法对56对PS点差分干涉图进行相位解缠,得到的解缠结果相对于MCF算法而言,解缠误差得到了很大改善,有20对解缠结果是完全正确的,如图 10所示。可看到本文得到的解缠相位比MCF结果更加平滑,原来的跳变点处的相位也变得连续了,证明本算法能有效解决桥梁区域相位解缠问题。

|
Download:
|
| 图 10 MCF算法解缠结果(a-c)和对应的本文算法解缠结果(d-f) Fig. 10 The unwrapped results by MCF method (a-c) and the proposed method (d-f) | |
除上述正确的干涉图外,剩下的干涉图只解决了部分误差问题,仍存在一些较小的误差,主要由于桥面残差点分布比较复杂,很难完全避免枝切线穿过桥面。对桥梁上的相位而言,必须保证完全没有误差,才能正常获取形变信息。为获得更多完全正确的解缠相位图,后续还需要采用更为有效的约束条件,来限制残差点的连接方式,从而解决桥梁形变测量的难题。
3 总结本文针对现有相位解缠方法在大型桥梁区域存在较大解缠误差的问题,提出一种改进的解缠算法,通过构建约束三角网络,降低残差点数量,随后又利用残差点分块方法,避免残差点穿过桥面,保持较短的枝切线,同时降低匹配优化难度,最后采用二分图最优权匹配方法,得到残差点的最优连接。该算法尤其适合在桥梁这类线状区域进行相位解缠,能有效降低解缠误差,提高解缠相位精度。
由于桥面残差点分布复杂,即便采用本文提出的约束方法,仍不能确保连接线不穿过桥面,需要后续对该问题进行更深入的分析,寻找更好的约束条件,来解决桥面PS点相位解缠误差问题,从而更好地获取大型桥梁形变信息。
| [1] |
Ferretti A, Prati C, Rocca F. Permanent scatterers in SAR interferometry[J]. IEEE Transanction on Geoscience and Remote Sensing, 2001, 39(1): 8-20. DOI:10.1109/36.898661 |
| [2] |
刘国祥, 陈强. 永久散射体雷达干涉理论与方法[M]. 北京: 科学出版社, 2012.
|
| [3] |
Costantini M. A novel phase unwrapping method based on network programing[J]. IEEE Transaction on Geoscience and Remote Sensing, 1998, 36(3): 813-821. DOI:10.1109/36.673674 |
| [4] |
Ghiglia D, Pritt M. Two-dimensional phase unwrapping:theory, algorithms, and software[M]. New York: Wiley, 1998.
|
| [5] |
Chen C. Statistical-cost network-flow unwrapping for radar interferometry[D]. Stanford: Stanford University, 2001.
|
| [6] |
Chen C W, Zebker H A. Network approaches to two-dimensional phase unwrapping:intractability and two new algorithms[J]. Journal of the Optical Society of America A, Optics, image science, 2000, 17(3): 401-414. DOI:10.1364/JOSAA.17.000401 |
| [7] |
于勇, 王超, 张红, 等. 基于不规则网络下网络流算法的相位解缠方法[J]. 遥感学报, 2003, 7(6): 472-477. |
| [8] |
魏志强, 金亚秋. 基于蚁群算法的InSAR相位解缠算法[J]. 电子与信息学报, 2008, 30(3): 518-523. |
| [9] |
Hooper A, Zebker H. Phase unwrapping in three dimensions with applications to InSAR time series[J]. Journal of the Optical Society of America A, Optics, image science, 2007, 24(9): 2737-3747. DOI:10.1364/JOSAA.24.002737 |
| [10] |
Costantini M, Malvarosa F, Minati F. A general formulation forredundant integration of finite differences and phase unwrapping on a sparse multidimensional domain[J]. IEEE Transaction on Geoscience and Remote Sensing, 2012, 50(3): 758-768. DOI:10.1109/TGRS.2011.2162630 |
| [11] |
Yu H, Li Z, Bao Z. A fast phase unwrapping method for large-scale interferograms[J]. IEEE Transaction on Geoscience and Remote Sensing, 2013, 51(7): 4240-4248. DOI:10.1109/TGRS.2012.2229284 |
| [12] |
Martinez-Espla J J, Martinez-Marin T, Lopez-Sanchez J M. A particle filter approach for InSAR phase filtering and unwrapping[J]. IEEE Transaction on Geoscience and Remote Sensing, 2009, 47(4): 1197-1211. DOI:10.1109/TGRS.2008.2008095 |
| [13] |
Huang Q, Zhou H, Dong S, et al. Parallel branch-cut algorithm based on simulated annealing for large-scale phase unwrapping[J]. IEEE Transaction on Geoscience and Remote Sensing, 2015, 53(7): 3833-3846. DOI:10.1109/TGRS.2014.2385482 |
| [14] |
Loffeld O, Nies H, Knedlik S, et al. Phase unwrapping for SAR interferometry:a data fusion approach by Kalman filtering[J]. IEEE Transaction on Geoscience and Remote Sensing, 2008, 46(1): 47-58. DOI:10.1109/TGRS.2007.909081 |
| [15] |
Yu H, Li Z, Bao Z. Residues cluster-based segmentation and outlier-detection method for large-scale phase unwrapping[J]. IEEE Transaction on Image Processing, 2011, 20(10): 2865-2875. DOI:10.1109/TIP.2011.2138148 |
| [16] |
Liu G, Wang R, Deng Y, et al. A new quality map for 2-D phase unwrapping based on gray level co-occurrence matrix[J]. IEEE Geoscience and Remote Sensing Letter, 2014, 11(2): 444-448. DOI:10.1109/LGRS.2013.2264857 |
| [17] |
杨磊, 赵拥军, 王志刚. 最小生成树相位解缠中冗余去除算法[J]. 遥感学报, 2006, 10(6): 879-884. |
| [18] |
张妍, 冯大政, 曲小宁, 等. 基于改进粒子群算法的二维相位解缠算法[J]. 电波科学学报, 2012(27): 1166-1123. |
 2019, Vol. 36
2019, Vol. 36 


