逆合成孔径雷达(inverse synthetic aperture radar，ISAR)成像技术通过距离向脉冲压缩和方位向目标的相对运动形成合成孔径，将目标场景的散射特性映射为方位-距离平面^[1-2]。随着压缩感知(compressed sensing，CS)^[3-4]理论的提出和完善，稀疏重构方法在雷达成像中得到越来越多的应用^[5]。与匹配滤波方法相比，稀疏重构方法可以通过较少的测量数据恢复目标场景。在稀疏重构模型中，L₁范数最小化方法是一种常见的选择^[6]，但是L₁惩罚项为重构结果带来了一定的误差，尤其是对目标的后向散射截面积有一定程度的低估^[7]。对于上述问题，可以利用非凸优化惩罚项进行稀疏重构，避免对目标后向散射截面积的低估。但是基于非凸优化惩罚项的重构模型往往为非凸函数，容易收敛到局部极小值^[8]。广义最小最大凹优化^[9](generalized minimax concave, GMC)惩罚项是一种非凸惩罚项，但是基于GMC惩罚项的最小二乘损失函数是凸优化函数，所以基于GMC的重构模型既有非凸优化重构的高精度的特点，又避免了迭代收敛到局部最小值。

本文将基于GMC的重构模型引入ISAR成像当中，然后用前向-后向算法^[10]求解该模型。与基于L₁范数最小化方法的重构结果相比，该方法避免了对ISAR中目标后向散射截面积的低估，有更高的幅度重构精度。仿真和实际数据处理结果验证了本文方法的有效性。

1 基于压缩感知的ISAR成像模型

ISAR成像转台模型如图 1所示。假设雷达发射线性调频信号为

$ s\left( t \right) = {\rm{rect}}\left( {\frac{{\hat t}}{{{T_{\rm{p}}}}}} \right)\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}\left( {{f_{\rm{c}}}t + \frac{\gamma }{2}{{\hat t}^2}} \right)} \right), $

(1)

式中：rect(·)是矩形时间窗；T_p是脉冲持续时间；f_c为中心频率；γ为信号调频率；$ \hat t$为快时间，t_m为慢时间，与全时间t的关系为：$ t = \hat t + {t_m}$。散射点$p({x_p}, {y_p}) $的回波信号经过基于匹配滤波的距离脉压后，可得到

$ \begin{array}{*{20}{c}} {s\left( {\hat t,{t_m}} \right) = {\sigma _{\rm{p}}} \times \sin c\left[ {{T_{\rm{p}}}\gamma \left( {\hat t - \frac{{2{R_{\rm{p}}}\left( {{t_m}} \right)}}{c}} \right)} \right] \times }\\ {\exp \left( { - {\rm{j}}\frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }{R_{\rm{p}}}\left( {{t_m}} \right)} \right),} \end{array} $

(2)

式中：λ表示信号波长，c为光速，σ_p为散射点p的反射系数。通常情况下ISAR目标由多个散射中心组成，假设散射中心数为P，公式(2)可进一步写为

$ \begin{array}{*{20}{c}} {s\left( {\hat t,{t_m}} \right) \approx \sum\limits_{p = 1}^P {{\sigma _{\rm{p}}}} \times \sin c\left[ {{T_{\rm{p}}}\gamma \left( {\hat t - \frac{{2\left( {{R_0} + {y_{\rm{p}}}} \right)}}{c}} \right)} \right] \times }\\ {\exp \left( { - {\rm{j}}\frac{{4{\rm{ \mathsf{ π} }}{x_{\rm{p}}}\omega {t_m}}}{\lambda }} \right) \times \exp \left( { - {\rm{j}}\frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\left( {{R_0} + {y_{\rm{p}}}} \right)} \right).} \end{array} $

(3)

当目标尺寸较大时，需要对$ s(\hat t, {t_m})$进行越距离单元走动校正，克服包络偏移。进一步对上式作关于慢时间t_m的傅里叶变换，可得到目标在距离-多普勒域的成像结果为

$ \begin{array}{*{20}{c}} {s\left( {\hat t,{f_{\rm{d}}}} \right) = \sum\limits_{p = 1}^P {{\sigma _{\rm{p}}}} \times \sin c\left[ {{T_{\rm{p}}}\gamma \left( {\hat t - \frac{{2\left( {{R_0} + {y_{\rm{p}}}} \right)}}{c}} \right)} \right] \times }\\ {\sin c\left[ {{T_{\rm{a}}}\left( {{f_{\rm{d}}} - {f_{\rm{p}}}} \right)} \right] \times \exp \left( { - {\rm{j}}\frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\left( {{R_0} + {y_{\rm{p}}}} \right)} \right),} \end{array} $

(4)

式中：f_p表示第p个散射中心的多普勒频率，T_a为方位向积累时间。对慢时间t_m和多普勒频率f_d离散化，可得${t_m} = [1:M]\cdot\Delta {t_m}, {f_{\rm{d}}} = [1:M]\cdot\Delta {f_{\rm{d}}}, M $为方位向采样点数。建立傅里叶矩阵F_M为

$ {\mathit{\boldsymbol{F}}_M} = \left[ {{\phi _1},{\phi _2}, \cdots ,{\phi _M}} \right],{\phi _m} = \exp \left( { - {\rm{j}}\frac{{2{f_{\rm{d}}}\left( m \right){t_m}}}{\lambda }} \right). $

(5)

令$ \mathit{\boldsymbol{s}} = {\rm{vec}}(s(\hat t, {t_m}))$，考虑加性噪声影响，矩阵形式如下所示

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{s}} = \left[ {\begin{array}{*{20}{c}} {{F_M}}&{}&{}&{}\\ {}&{{F_M}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{F_M}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\sigma \left( {1,1} \right)}\\ {\sigma \left( {1,2} \right)}\\ \vdots \\ {\sigma \left( {1,M} \right)}\\ \vdots \\ {\sigma \left( {N,M} \right)} \end{array}} \right] + \mathit{\boldsymbol{n}}}\\ { = \mathit{\boldsymbol{F\sigma }} + \mathit{\boldsymbol{n}},} \end{array} $

(6)

式中:σ表示后向散射系数向量，n表示加性噪声向量。

ISAR图像是目标在距离-多普勒2维平面的分布，ISAR目标尺寸有限，在较小的观测角度内，ISAR图像可以认为由散射点组成，并且强散射点仅占整个成像平面非常少的像素单元，这说明ISAR图像有很强的稀疏性。式(6)即为基于稀疏处理的ISAR成像模型。进一步要获得ISAR的成像结果，实际上就是对式(6)进行求解。上式是典型的压缩感知模型，采用稀疏重构算法即可得到后向散射系数σ，将σ重新排成二维矩阵即是目标的ISAR成像结果。

2 ISAR稀疏重构方法 2.1 L₁范数最小化方法

稀疏重构方法有凸优化方法^[11]、非凸优化方法^[12]、贪婪算法^[13]和贝叶斯算法^[14]，其中较为常用的是基于L₁范数的凸优化方法。

通常使用的方法是加入正则项使最小二乘损失函数最小化，即

$ \min \frac{1}{2}\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{F\sigma }}} \right\|_2^2 + \lambda \varphi \left( \mathit{\boldsymbol{\sigma }} \right), $

(7)

其中λ为正则化参数，当惩罚项为L₁范数时，可以用迭代软阈值算法(iterative shrinkage-thresholding，IST)对上式进行求解^[15-16]。迭代公式如下

$ {x^{\left( {i + 1} \right)}} = {f_{\lambda \mu }}\left( {{x^i} - \mu {\mathit{\boldsymbol{F}}^{\rm{H}}}\left( {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{F}}{x^i}} \right)} \right), $

(8)

其中

$ {f_{\lambda \mu }}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {{\rm{sign}}\left( x \right)\left( {x - \lambda \mu } \right),}&{\left| x \right| \ge \lambda \mu }\\ {0,}&{\left| x \right| < \lambda \mu } \end{array}} \right., $

(9)

式中：μ为控制收敛性的参数，sign为符号函数，软阈值函数如图 2(a)所示。

2.2 GMC惩罚项方法

GMC是最小最大凹(minimax concave, MC)惩罚项的一种推广^[9]。本文以MC惩罚项^[17]来推导GMC方法避免幅值系统性低估的原理。在下面这个式子中，令λ>0且$a\in \mathbb{R} $

$ f\left( x \right) = \frac{1}{2}{\left( {y - ax} \right)^2} + \lambda {\varphi _{\rm{b}}}\left( x \right), $

(10)

其中，MC惩罚项的φ_b等于

$ {\varphi _{\rm{b}}}\left( x \right) = \left\{ \begin{array}{l} \left| x \right| - \frac{1}{2}{b^2}{x^2},\;\;\;\;\left| x \right| \le 1/{b^2}\\ \frac{1}{{2{b^2}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| x \right| > 1/{b^2} \end{array} \right., $

(11)

如果b²≤a²/λ，那么f就是凸函数。当f为凸函数时，f的极小值由firm阈值函数给出

$ \begin{array}{*{20}{c}} {{\rm{firm}}\left( {y;{\lambda _1},{\lambda _2}} \right) = }\\ {\left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| y \right| < {\lambda _1}\\ {\lambda _2}\frac{{\left| y \right| - {\lambda _1}}}{{{\lambda _2} - {\lambda _1}}}{\rm{sign}}\left( y \right),\;\;\;\;\;{\lambda _1} \le \left| y \right| \le {\lambda _2},\\ y,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| y \right| > {\lambda _2} \end{array} \right.} \end{array} $

(12)

其中，λ₁>0，λ₂>λ₁为自由调节参数，当λ₂→λ₁或者λ₂→∞时，firm阈值函数分别接近于硬阈值或者软阈值函数，firm函数如图 2(b)所示。在恢复较大幅值时，firm阈值函数保证了其原有值大小，所以它不会导致高幅值的低估^[9]。

将MC惩罚项推广到多元，即GMC。令$ \mathit{\boldsymbol{B}}\in {{\mathbb{R}}^{M\times N}}$，B为由F约束的一个参数矩阵，GMC惩罚项定义如下

$ {\varphi _B}\left( x \right) = \left\| x \right\| - {S_B}\left( x \right), $

(13)

其中，

$ {S_B}\left( x \right) = \mathop {\inf }\limits_{v \in {R^N}} \left\{ {{{\left\| v \right\|}_1} + \frac{1}{2}\left\| {B\left( {x - v} \right)} \right\|_2^2} \right\}. $

(14)

对于给定$ \mathit{\boldsymbol{B}}\in {{\mathbb{R}}^{M\times N}}$，GMC惩罚项满足

$ {\varphi _B}\left( x \right) = {\left\| x \right\|_1} - \frac{1}{2}\left\| {\mathit{\boldsymbol{B}}x} \right\|, $

(15)

当且仅当$ \parallel {\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{B}}x{\parallel _\infty } \le 1$，这个结果意味着在0附近GMC惩罚项近似于L₁范数。

考虑设计能够维持正则化最小二乘损失函数凸性的GMC惩罚项，令$ y\in {{\mathbb{R}}^{M}}, F\in {{\mathbb{R}}^{M}}$且λ>0，定义$ G:{{\mathbb{R}}^{N}}\to \mathbb{R}$

$ G\left( x \right) = \frac{1}{2}\left\| {y - Fx} \right\|_2^2 + \lambda {\varphi _B}\left( x \right), $

(16)

其中φ_B为GMC惩罚项。如果

$ {\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{B}} \le \frac{1}{\lambda }{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{F}}, $

(17)

那么G则为一个凸函数，对于给定的F，令

$ \mathit{\boldsymbol{B}} = \sqrt {\gamma /\lambda } \mathit{\boldsymbol{F}},0 \le \gamma \le 1, $

(18)

当γ≤1时, $ {\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{B}} = \left( {\gamma /\lambda } \right){\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{F}}$满足式(17)，在实践中，γ的取值通常在0.5~0.8^[9]。当B满足式(17)时，为了能够使用近似算法去最小化损失函数G，将G重写为一个鞍点问题：

$ \left( {{x^{{\text{opt}}}},{v^{{\text{opt}}}}} \right) = \arg \mathop {\min }\limits_{x \in {\mathbb{C}^N}} \mathop {\max }\limits_{v \in {\mathbb{C}^N}} G\left( {x,v} \right), $

(19)

其中

$ \begin{array}{*{20}{c}} {G\left( {x,v} \right) = \frac{1}{2}\left\| {y - \mathit{\boldsymbol{F}}x} \right\|_2^2 + \lambda {{\left\| x \right\|}_1} - \lambda {{\left\| v \right\|}_1} - }\\ {\frac{\gamma }{2}\left\| {\mathit{\boldsymbol{F}}\left( {x - v} \right)} \right\|_2^2,} \end{array} $

(20)

式(20)的解由前向-后向算法获得，前向后向问题仅包括简单的计算步骤，其算法流程如表 1所示。

3 实验及结果分析

下面通过仿真数据和实测数据验证本文的基于GMC惩罚项的ISAR稀疏重构方法重构效果。仿真实验通过与传统RD成像方法和IST算法的对比，验证基于GMC惩罚项方法提高幅值精度的能力。实测数据实验中，从恢复性能和抗噪声性能两方面比较IST重构算法和GMC重构算法，验证本文算法的优越性。

3.1 仿真数据实验

在仿真数据中，仿真场景为12个点目标组成的飞机，雷达中心频率f_c=10GHz，系统带宽B=400MHz，点目标匀速转动，对所得到的回波进行20%降采样，所得RD成像结果如图 3(a)所示。使用IST算法稀疏重构的结果如图 3(b)所示。采用改进L₁范数方法的GMC算法成像结果如图 3(c)所示。

从图 3可以看出，使用RD、IST算法和GMC算法均可实现仿真场景成像，与RD成像结果相比，IST算法和GMC算法对旁瓣的抑制能力均优于RD结果。为探究IST算法和GMC算法的成像精度能力，依然使用上述成像场景，改变回波信噪比，分别使用IST算法和GMC算法进行成像，计算成像结果中幅值与真实值之间的误差，为方便比较，成像结果均经归一化处理，其误差曲线如图 4所示。

从误差曲线可以看出，随着噪声的增大，两种精度误差曲线均呈上升趋势，但是误差估计仍然与高信噪比条件下处于同一数量级，而GMC算法在信噪比一定的条件下，其成像精度要高于IST算法，且随着信噪比的降低，GMC算法的成像精度更稳定。由此可见，GMC算法具备更高的成像误差精度估计。

3.2 实测数据实验

首先从成像能力方面验证GMC算法的有效性，下面使用一组实测数据进行处理。实测数据为ISAR系统记录的Yak-42飞机回波信号，信号带宽为400MHz，载频为5.52GHz，脉冲重复频率为100Hz，经过包络对齐和自聚焦处理后的数据大小为256×1024，进行20%降采样处理。回波数据经过IST算法和GMC算法处理后，成像结果如图 5所示，从图中可以看出，两种方法均可实现对Yak-42飞机的稀疏成像。

为了进一步验证GMC算法在成像精度方面的优势，下面通过对原始数据添加高斯白噪声，使其信噪比为0，5和10dB。在不同信噪比下对降采样20%数据分别使用IST算法重构和GMC算法重构处理，得到如图 6所示图像，图 6分别为IST重构和GMC重构两种算法在不同信噪比下的成像结果。

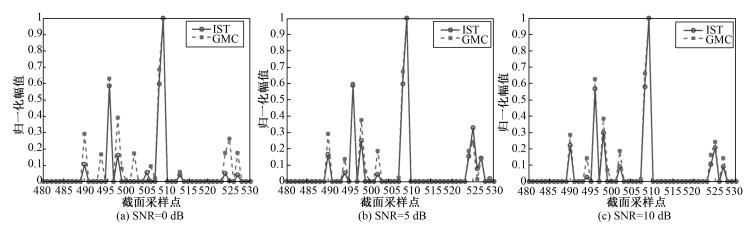
为分析GMC算法在保持幅值精度的能力方面，选取图 6中不同信噪比条件下相同部分的切面，归一化幅值比较如图 7所示，可以看到，在信噪比为10dB时，两种算法均实现了目标点的准确成像，但是IST算法成像结果存在整体性幅值低估的情况，而GMC算法成像结果则不存在上述误差，具有更低的幅值精度估计误差。随着信噪比的降低，IST算法成像切面出现幅值偏差，当信噪比为0dB时出现虚假目标点，而GMC算法在低信噪比的条件下依然保持了成像结果的幅值特性，由此可见，GMC算法在保持成像幅值精度方面更有优势。

4 结论

由于已有的基于L₁范数最小化方法在ISAR稀疏成像中存在重建幅值精度上的偏差，因此，本文提出将基于GMC惩罚项的方法应用于ISAR稀疏成像，通过对仿真和实测数据的比较分析，验证了该方法在稀疏重构中保持目标回波幅值的能力，且在信噪比变化较大的情况下仍具有良好的聚焦性能。与IST算法相比，本文方法在重建幅值精度上重建精度高，优势明显。