2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,小型无人机变得越来越普遍,在军事领域和民用领域都得到广泛应用。但与此同时,由于其价格低廉、操作简单,也被滥用于不安全、甚至犯罪的行为,对国家经济发展和国民安全构成实际威胁[1]。因此,针对小型无人机目标的识别具有重要的应用价值。无人机的独特之处在于,几乎所有无人机都有一个及以上数目的螺旋桨。旋翼的旋转叶片会对雷达的后向散射信号产生周期性的频率调制,在无人机自身多普勒谱的两边产生边带,这种附加的多普勒频率调制被称为微多普勒效应[2-3]。
利用微多普勒特征识别小型无人机已成为研究热点。文献[3-5]研究不同型号无人机的微多普勒特征,提出基于频谱图的无人机分类方法,并通过实验证明微多普勒特征在识别小型无人机时可以作为多普勒特征的一个补充特征,但文章未涉及无人机微多普勒参数的提取方法。文献[6-7]研究多旋翼无人机的微多普勒模型,并对散射点积分回波模型和物理光学眼面回波模型进行比较,分析极化特性对微多普勒的影响,但没有讨论叶片数、转速、初始相位等对微多普勒的影响。文献[8-10]研究旋翼数、转动频率、叶片数及叶片长度的提取方法,但在实际场景中利用旋翼调制谱线估计叶片数较难,而采用倒频谱估计旋翼数及转速需要较多的有效脉冲回波数,运算速度较慢且精度不够高。
四旋翼无人机是目前最常见的无人机类型,本文以四旋翼无人机为研究对象,对小型无人机的微多普勒特性与特征提取进行研究。首先建立多旋转旋翼的回波模型,并通过仿真实验分析叶片数目、旋翼转速和初始相位等参数对微多普勒特征的影响,接着提出一种基于Gabor变换的瞬时频率估计与FFT相结合的微动特征提取算法。该算法利用Gabor变换得到时频特征,在此基础上通过瞬时频率极大值法提取微多普勒频率展宽,并对瞬时频率采用FFT提取旋翼数和转动频率,由此得到叶片长度估计值。大疆精灵3S无人机的实测数据验证了算法的有效性,能较为准确地提取无人机的微动参数。
1 多旋翼无人机回波建模美国海军实验室的Victor C. Chen教授建立了旋转旋翼叶片回波的积分模型。对于多旋翼的无人机,假设各旋翼叶片的RCS相同且均为1,在直升机旋翼模型[2]基础上,本文构建出多旋转旋翼的回波模型如下:
| $ \begin{array}{*{20}{c}} {{s_\mathit{\Sigma }}\left( t \right) = \sum\limits_{m = 1}^M {L\exp \left\{ { - {\rm{j}}\frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\left[ {{R_{{0_m}}} + {z_{{0_m}}}\sin {\beta _m}} \right]} \right\}} \cdot }\\ {\sum\limits_{k = 0}^{N - 1} {\sin c\left\{ {\frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\frac{L}{2}\cos {\beta _m}\cos \left( {{\Omega _m}t + {\varphi _{{0_m}}} + k2{\rm{ \mathsf{ π} }}/N} \right)} \right\}} \cdot }\\ {\exp \left\{ { - j{\Phi _{m,k}}\left( t \right)} \right\},} \end{array} $ | (1) |
其中
| $ \begin{array}{*{20}{c}} {{\mathit{\Phi }_{m,k}}\left( t \right) = \frac{{4{\rm{ \mathsf{ π} }}}}{\lambda }\frac{L}{2}\cos {\beta _m}\cos \left( {{\mathit{\Omega }_m}t + {\varphi _{{0_m}}} + k2{\rm{ \mathsf{ π} }}/N} \right),}\\ {\left( {k = 0,1,2, \cdots ,N - 1;m = 1,2, \cdots ,M} \right).} \end{array} $ | (2) |
式中:M为旋翼总数目,N为单个旋翼总的叶片数目,L表示旋翼叶片长度,R0m为雷达到第m个旋翼中心的距离,z0m表示第m个旋翼叶片的高度,βm为雷达到第m个旋翼中心的俯仰角(近似等于雷达到无人机轴中心的俯仰角,即β1=β2=…=βM=β),Ωm为第m个旋翼的转动角频率,φ0m为第m个旋翼的初始旋转角。
回波信号的瞬时多普勒频率可由信号的相位函数求时间导数得到,对式(2)求时间导数得到第m个旋翼的第k个叶片的等效瞬时微多普勒频率为
| $ {f_{m,k}}\left( t \right) = - \frac{{L{\mathit{\Omega }_m}}}{\lambda }\cos \beta \sin \left( {{\mathit{\Omega }_m}t + {\varphi _{{0_m}}} + k2{\rm{ \mathsf{ π} }}/N} \right). $ | (3) |
而叶片上的一个散射点P的瞬时多普勒频率是
| $ {f_{m,k,P}}\left( t \right) = - \frac{{2{l_P}{\mathit{\Omega }_m}}}{\lambda }\cos \beta \sin \left( {{\mathit{\Omega }_m}t + {\varphi _{{0_m}}} + k2{\rm{ \mathsf{ π} }}/N} \right). $ | (4) |
式中:lP为散射点P到旋翼旋转中心的距离,且0≤lP≤L。
式(4)表明,叶片上散射点的微多普勒频率是正弦变化的曲线,曲线条数即叶片数目,且正弦曲线频率ω与叶片转动角频率相同,则有
| $ {\omega _{m,k}} = {\mathit{\Omega }_m}. $ | (5) |
叶片叶尖处的多普勒频率幅度值最大,则最大微多普勒频率为
| $ {f_{md{\rm{Max}}}} = - \frac{{2L{\mathit{\Omega }_m}}}{\lambda }\cos \beta . $ | (6) |
目标平动速度为0时,叶片的微多普勒频率的最大展宽为
| $ {f_{W - \max }} = {f_{md{\rm{Max}}}} - {f_{md{\rm{Min}}}} = 2{f_{md{\rm{Max}}}} = 2 \times \frac{{2L{\mathit{\Omega }_m}}}{\lambda }\cos \beta . $ | (7) |
由此推导出旋翼的叶片长度为
| $ L = \frac{{\lambda {f_{W - \max }}}}{{4{\mathit{\Omega }_m}\cos \beta }}. $ | (8) |
通过估计的旋翼数、叶片数、叶片长度、旋翼转速等参数可判断无人机型号和运动状态,达到识别多旋翼无人机的目的。
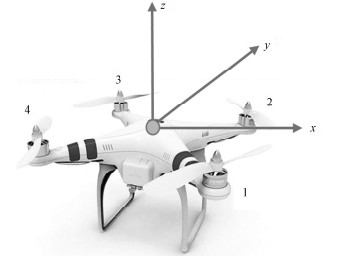
2 多旋翼无人机微多普勒特性分析本文以四旋翼无人机为典型目标进行微多普勒特性分析和特征提取,四旋翼无人机结构如图 1所示,其中旋翼1、3逆时针方向旋转,旋翼2、4顺时针方向旋转。
|
Download:
|
| 图 1 四旋翼飞行器的结构示意图 Fig. 1 Diagram of four-rotor UAV | |
由式(3)可知,多旋翼无人机微多普勒特征是由M×N条正弦形式的曲线组成,且受到载频、旋翼数目、旋翼转速、叶片数、叶片长度、初始相位和俯仰角的影响。其中,载频、叶片长度和俯仰角仅与微多普勒频率幅度有关,而旋翼数目、旋翼转速、叶片数和初始相位将影响微多普勒特征曲线的幅度和相位,下面对主要参数的影响进行仿真分析。
2.1 不同叶片数目对微多普勒特性的影响由式(3)可知,多旋翼无人机微多普勒特征曲线条数及相位与叶片数目有关。
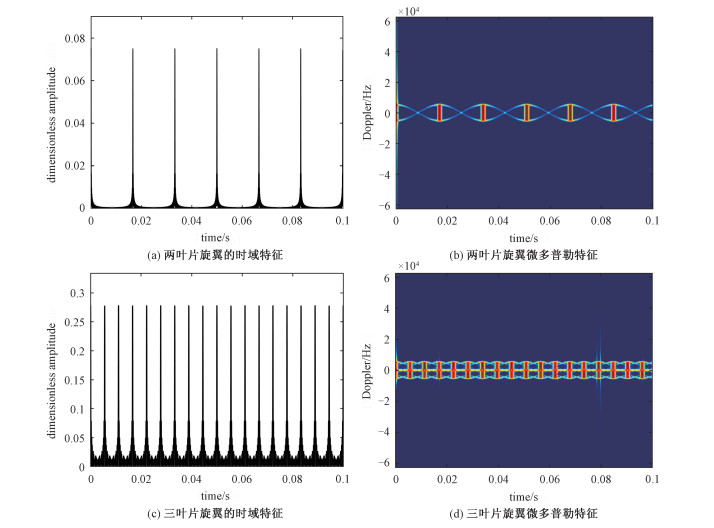
设雷达微波为Ka波段,载波频率为34.6 GHz,带宽为1.2 GHz,脉冲重复频率PRF为125 kHz。雷达俯仰角β为10°,方位角α为0°,雷达到无人机轴中心距离是100 m,无人机运动速度为0,旋翼数目为4个,各旋翼叶片的初始旋转角φ0为0°,旋翼转动速度均为30 r/s,各旋翼旋转中心至无人机轴中心距离15 cm,叶片长度为12 cm,观测时长0.1 s。采用式(1)仿真多旋翼散射点积分的回波模型,采用Gabor变换对不同叶片数目的旋翼微多普勒信号进行仿真,结果如图 2所示。
|
Download:
|
| 图 2 不同叶片数的四旋翼无人机微多普勒特征 Fig. 2 Micro-Doppler characteristics of four-rotor UAVs with two and three blades | |
分析式(1)和图 2(a)、2(b),在时域回波出现sinc峰值的时刻,对应的时频域会有一条频率带,是时频域闪烁现象,在叶片与雷达视线垂直时刻产生[11-12];由图 2知,四旋翼无人机回波的时域闪烁和对应的时频域闪烁次数相同,闪烁频率为fT=kNfr(fr为转动频率,N为叶片数,N为奇数时,k取2;N为偶数时,k取1)[13],2叶片0.1 s内出现6次闪烁,3叶片0.1 s内出现18次闪烁,可估计出叶片转动频率30 Hz;从图 2(b)、2(d)发现,四旋翼无人机叶片的微多普勒关于平均多普勒频率对称,原因是四旋翼无人机有两组旋转方向相反的旋翼,产生的微多普勒频率相反,而在叶片数为3时有明显的零频带;图 2(b)提取的微多普勒频率最大展宽值为fW-max=5 259×2=10 518 Hz,再根据式(8)计算得到叶片长度为L=12.28 cm,叶长估计值的相对误差为2.33 %,验证了理论分析的正确性。
2.2 不同旋翼转速对微多普勒特性的影响由式(3)可知,多旋翼无人机旋翼的转速会影响微多普勒频率的幅度大小及微多普勒特征曲线的频率。
在2.1节的仿真参数下,假定各旋翼叶片数设为2,观测时间设为0.2 s,设置不同的旋翼转速,仿真多旋翼散射点积分的回波模型,用Gabor变换进行微多普勒仿真。旋翼1、3转速相等(30 r/s),旋翼2、4转速相等(35 r/s)时微多普勒仿真结果为图 3。

|
Download:
|
| 图 3 不同转速的四旋翼无人机微多普勒特征 Fig. 3 Micro-Doppler characteristics of four-rotor UAV with different rotation rates | |
4个旋翼转速相同时,各旋翼微多普勒特征重合,且只有唯一的时频闪烁周期,如图 2(b)所示,而图 3出现不同的闪烁周期,表明旋翼数不只一个;图 3中明显看出两种不同频率的正弦曲线,其中频率较小的时频闪烁次数为m1=12,对应的转动频率为fr1=30 Hz,微多普勒频率的最大值为fmdMax1=5 259 Hz,频率较大的时频闪烁次数为m2=14,对应的转动频率为fr2=35 Hz, 微多普勒频率的最大值为fmdMax=6 238 Hz, 有m1/m2=fr1/fr2=0.857 1,fmdMax1/fmdMax2=0.843 1≈fr1/fr2,则微多普勒特征的时频闪烁频率之比等于旋翼转动频率之比,微多普勒峰值频率与叶片转动频率成正比。综合以上分析,旋翼转动频率会影响微多普勒频率的幅度、时频闪烁的周期及次数。
2.3 不同初始相位对微多普勒特性的影响由式(3)知,多旋翼无人机各旋翼叶片的初始相位影响微多普勒特征曲线的相位。
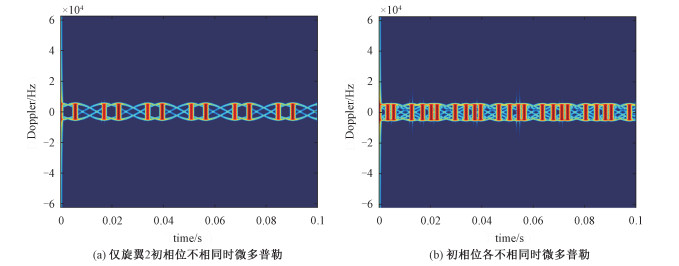
在2.1节的仿真参数下,假定各旋翼叶片数设为2,设置不同的旋翼初始相位,仿真多旋翼散射点积分的回波模型,采用Gabor变换提取旋翼的微多普勒信息。旋翼2初始相位为60°,旋翼1、3、4初始相位相同(0°)时微多普勒仿真结果为图 4(a);各旋翼初始相位各不相同时微多普勒仿真结果为图 4(b)。
|
Download:
|
| 图 4 不同初始相位的四旋翼无人机微多普勒特征 Fig. 4 Micro-Doppler characteristics of four-rotor UAV with different initial phases | |
图 2(b)中4个旋翼初始相位相同时,微多普勒特征曲线重合;对比图 4(a)、4(b),当旋翼初始相位不同时,微多普勒特征曲线的初始相位不同,且时频闪烁时刻出现差异,使得微多普勒特征曲线周期发生变化。图 2(b)第2次时频闪烁时刻是在0.022 61 s,而图 4(a)仅旋翼2初相位改变时出现新的时频闪烁,其第2次时频闪烁时刻是在0.016 94 s,时间间隔为Δt=0.005 7 s,根据时频闪烁频率fT=30 Hz可得两次闪烁的初始相位差为Δφ0=2πfTΔt=61.236°,接近仿真值60°。从上述分析可知,旋翼叶片不同的初始相位会改变微多普勒峰值出现的时刻及闪烁次数,不改变闪烁周期,可通过对无人机不同角度的照射得到有相位差异的微多普勒特征曲线,进而对叶片数的判断提供参考。
通过以上对多旋翼无人机微多普勒特征的建模和仿真分析,弄清微多普勒特征的影响因素,为后文的微多普勒特征提取及参数估计提供理论基础。
3 多旋翼无人机微多普勒特征提取微多普勒信号是非平稳信号,而传统的傅里叶变换不能得到与时间有关的频率信息,联合时频分析提供了一种分析信号瞬时频率随时间变化规律的方法[11]。时频分析方法主要包括线性变换法和双线性变换法。线性时频分析法主要有如短时傅里叶变换(STFT)、Gabor变换、分数阶傅里叶变换(FRFT)等,双线性时频分析法有Wigner-Ville分布(WVD)、伪WVD分布、平滑伪WVD分布、广义S变换等。这些方法都有各自的优缺点。例如STFT是最常用的时频分析法,其实现简单且无交叉项,但不能同时获得高的时间和频率分辨率;FRFT为参数搜索类方法,无交叉项的干扰,但进行匹配搜索运算量较大,且参数估计精度受搜索步长的限制,多用于分析chirp信号[14];平滑伪WVD分布是在WVD基础上产生的方法,对交叉项进行了较好的抑制,但计算量增加且时频分辨率下降[15];广义S变换时频分辨率较好且能有效抑制交叉项,但窗函数的双参数调节增加运算的复杂度。
多分量信号的时频分析中分辨率与交叉项存在矛盾,Gabor变换是一种特殊的STFT变换,不会产生交叉项,且运算简单,其采用高斯窗获得最小的时间和频率分辨率的乘积,时频特征明显。对于多旋翼无人机目标,其微多普勒信号为多分量信号,对实时性要求高,且时频特征要突出,因此考虑采用Gabor变换进行时频特征分析。
3.1 瞬时频率提取信号的时频分布代表信号的瞬时能量,其在时频面上的投影就是信号的瞬时频率[16]。多分量信号通过Gabor变换后,各分量信号的峰值在时频面上的投影等价于时频面的极大值,提取时频图的极大值即为各分量信号的瞬时频率。
设信号的离散Gabor分布Gabor(m, n)是M×N的矩阵,为了减小噪声的影响,将Gabor(m, n)通过设定的门限值,然后按列求得极大值,由此得到所有分量信号的瞬时频率[17],瞬时频率的表达式近似为
| $ {f_k}\left( i \right) = \mathop {\arg }\limits_{k,1 \le i \le N} \left\{ {Peak\left[ {Gabo{r_{M \times N}}\left( {:,i} \right)} \right]} \right\}. $ | (9) |
式中:fk(i)表示第i时刻第k个分量的瞬时多普勒频率,GaborM×N(:, i)表示M×N阵列的第i列,arg(·)表示取宗量运算,peak[·]为求极大值。若目标的径向平动速度引起的多普勒频移为fu,则瞬时微多普勒频率为:
| $ {f_{m,k}}\left( i \right) = {f_k}\left( i \right) - {f_u},1 \le i \le N. $ | (10) |
采用瞬时频率极大值法可以得到微多普勒频率的最大展宽值fW-max。
3.2 旋翼数和转动频率提取多旋翼无人机旋翼旋转产生的微多普勒信号是多个正弦函数组成,对其做傅里叶变换,则可得到各正弦函数的频率[16],即各旋翼的转动频率。当旋翼转速不同时,会得到不同的频率成分,可判断旋翼数目。因此,对无人机旋翼产生的微多普勒进行时间维的傅里叶变换得到的频谱图,可估计微多普勒信号的正弦频率及不同频率成分的个数。
对式(4)进行FFT变换,得到第m个旋翼的第k个叶片的傅里叶变换结果为
| $ \begin{array}{*{20}{c}} {{F_{m,k}}\left( \omega \right) = \frac{{{\rm{j \mathsf{ π} }}L{\mathit{\Omega }_m}}}{\lambda }\cos \beta \cdot }\\ {\left[ {{{\rm{e}}^{{\rm{j}}\left( {{\varphi _{{0_m}}} + k2{\rm{ \mathsf{ π} }}/N} \right)}}\delta \left( {\omega - {\mathit{\Omega }_m}} \right) - {{\rm{e}}^{ - {\rm{j}}\left( {{\varphi _{{0_m}}} + k2{\rm{ \mathsf{ π} }}/N} \right)}}\delta \left( {\omega + {\mathit{\Omega }_m}} \right)} \right].} \end{array} $ | (11) |
从式(11)可知,第m个旋翼的微多普勒傅里叶变换后的谱线应该出现在其转动频率处。
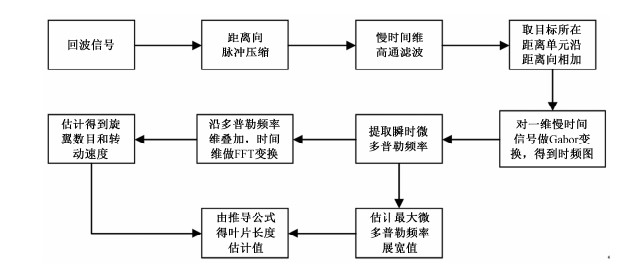
3.3 算法流程本文提出的多旋翼无人机微动特征提取算法的处理流程如图 5所示。
|
Download:
|
| 图 5 本文提出的微动特征提取算法流程图 Fig. 5 Flow chart of the proposed feature parameter extraction algorithm | |
算法的具体实现过程为:将接收的Ka波段调频连续波雷达回波脉冲按列存放为二维矩阵,对快时间维进行傅里叶变换(即脉冲压缩)得到距离维信息,慢时间维运用高通滤波抑制静止杂波,取二维矩阵中目标所在的距离单元沿距离维累加形成沿时间维的一维信号,对该一维信号进行Gabor变换则可得到目标的微多普勒信号。由微多普勒谱提取瞬时微多普勒频率来估计微多普勒频率展宽值,对提取的瞬时频率沿多普勒频率维叠加并进行时间维的傅里叶变换,由此可估计旋翼转动频率及旋翼数目,最后由公式(8)计算出叶片长度值。
3.4 性能分析与实测数据验证 3.4.1 性能分析在2.1节的仿真参数下,设叶片数为2,在未做积累的回波信号中分别加入信噪比为10、5、0、-5、-10、-11 dB的高斯白噪声,表 1是不同信噪比条件下微多普勒参数的提取结果,由20次仿真实验取得的估计均值。根据式(8)可得各旋翼叶片长度的估计值为
| $ {{\hat L}_m} = \frac{{\lambda {{\hat f}_{{{\left( {W - \max } \right)}_m}}}}}{{8{\rm{ \mathsf{ π} }}{{\hat f}_{{{\rm{r}}_m}}}\cos \beta }}. $ | (12) |
|
|
表 1 不同信噪比条件下微多普勒参数提取结果 Table 1 Results of micro-Doppler parameters extraction under different SNR conditions |
式中:
将各旋翼叶片长度估计值的均值作为无人机叶片长度的最终估计值:
| $ \hat L = mean\left( {{{\hat L}_1},{{\hat L}_2},{{\hat L}_3},{{\hat L}_4}} \right). $ | (13) |
叶长L估计值的相对误差为
| $ \Delta L = \left| {\frac{{\hat L - {L_{\rm{e}}}}}{{{L_{\rm{e}}}}}} \right| \times 100\% . $ | (14) |
式中:Le表示叶片长度的真实值。
从表 1可以看出,在信号信噪比低至-11 dB时,该算法仍能准确地提取出旋翼数目和各旋翼转速,具有一定的抗噪性;信噪比为-10 dB以上时,随着信噪比增大,叶片长度值的估计误差越来越小,且在-10 dB时估计误差也能达到14.08 %,而在-11 dB及以下信噪比条件下,由于噪声较强,时频图中的微多普勒特征很模糊,难以估计最大微多普勒频率的展宽值,故不能推导出叶片长度估计值。分析结果表明,本文提出的算法在低信噪比情况下,能实现无人机微多普勒参数的高精度提取。
3.4.2 四旋翼无人机悬停试验针对旋翼数目、转速、叶片长度的估计,进行检测悬停的大疆精灵3S无人机微多普勒特征的试验。试验使用Ka波段调频连续波雷达,载频为34.6 GHz,带宽1.2 GHz,PRF为125 kHz,雷达雷达定向照射,俯仰角约20°,雷达到无人机的距离约20 m左右。图 6为四旋翼无人机悬停试验数据处理结果。

|
Download:
|
| 图 6 四旋翼无人机悬停试验结果 Fig. 6 Test results for a hovering four-rotor UAV | |
图 6(a)是取1 s时频图做傅里叶变换的结果,使得频率分辨率达到Hz级,图中仅得到1种频率成分,为31 Hz,由式(11)可知其对应的微多普勒信号频率应为31 Hz,而对于2个叶片的四旋翼无人机,其微多普勒特征关于平均多普勒频率对称,则微多普勒信号的频率为转动频率的2倍,由此可知对应旋翼的转动频率应为15.5 Hz;图 6(b)的时频图中能明显看出两种不同相位的时频闪烁且间隔不均匀,说明至少有2个转速均为31 r/s的旋翼,而四旋翼无人机在悬停时4个旋翼转速相等[18],因此另2个旋翼转速均为15.5 r/s;从图 6(c)估计出微多普勒频率的最大展宽值为fW-max=2 568-(-2 324)=4 892 Hz,由公式(8)计算得到叶片长度估计值为11.92 cm,其真实值为12 cm,则叶长估计值的相对误差为0.67 %,试验证明该算法能有效提取四旋翼无人机的微动参数。
3.4.3 强杂波背景下四旋翼无人机慢速运动试验在强杂波背景中对空中慢速运动的大疆精灵3S无人机进行检测,无人机垂直于雷达视线运动,背景中有树木、小型建筑物、行人等,有3~4级风。雷达使用Ka波段调频连续波,载频为34.6 GHz,信号带宽为1.2 GHz,PRF为125 kHz,雷达定向照射,俯仰角约22°,雷达到无人机的距离约为25 m。根据采集的数据提取树木杂波背景中四旋翼无人机的微多普勒特征,回波信号脉压后的信杂比为-25 dB。在使用本文方法之前采用高通滤波对杂波进行抑制,滤波后的信杂比为-6 dB。图 7所示为强杂波背景下四旋翼无人机慢速运动试验处理结果。

|
Download:
|
| 图 7 强杂波背景下四旋翼无人机慢速运动试验结果 Fig. 7 Test results for a hovering four-rotor UAV in strong clutter background | |
图 7(a)得到2种频率成分,分别为46、61 Hz,对应的转动频率分别为23、30.5 Hz,则判断有2个转速分别为23、30.5 r/s的旋翼,由于四旋翼无人机在平移运动过程中有2对转速分别相同的旋翼[18],则另2个旋翼转速也分别为23、30.5 r/s;图 7(b)是由0.2 s信号的时频图提取的瞬时频率,各旋翼微多普勒频率交叉在一起,不宜直接估计微多普勒展宽频率,则从目标回波所在的多个距离单元中选取不同距离单元分别进行分析,结果如图 7(c)、7(d)所示;由图 7(c)、7(d)提取的最大微多普勒频率宽度分别是fW-max1=3 792-(-3 547)=7 339 Hz,fW-max2=4 281-(-5 015)=9 296 Hz,对应的旋转频率分别为23和30.5 Hz,根据式(8),估计出叶片长度分别是12.15和11.60 cm,相对误差分别为1.25 %和3.33 %,试验表明该算法对多旋翼无人机微动参数提取有较高的准确率, 且在杂波环境中也具有可行性。
4 结论本文在直升机旋翼回波模型的基础上,建立多旋翼无人机的回波模型,并基于该模型进行仿真实验,分析不同叶片数目、不同旋翼转速及不同初始相位对多旋翼无人机微多普勒特性的影响。针对多旋翼无人机目标,提出一种基于Gabor变换的瞬时频率估计与FFT相结合的微动特征提取算法,并通过四旋翼无人机悬停试验和强杂波背景下四旋翼无人机慢速运动试验验证了该方法的有效性,且对旋翼数、转速、叶片长度的估计都有较高的准确性。但对于无人机运动时转速不稳定的情况,该方法不再适用,在后续工作中将对这些情况进行研究。
| [1] |
Hoffmann F, Ritchie M, Fioranelli F, et al. Micro-Doppler based detection and tracking of UAVs with multistatic radar[C]//IEEE Radar Conference, 2016: 1-6.
|
| [2] |
Chen V C, Li F, Ho S S, et al. Micro-Doppler effect in radar:phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace & Electronic Systems, 2006, 42(1): 2-21. |
| [3] |
Jian M, Lu Z, Chen V C. Experimental study on radar micro-Doppler signatures of unmanned aerial vehicles[C]//Radar Conference, 2017: 854-857.
|
| [4] |
Wit J J M D, Harmanny R I A, Premel-Cabic G. Micro-Doppler analysis of small UAVs[C]//European Radar Conference, 2012: 210-213.
|
| [5] |
Nanzer J A, Chen V C. Microwave interferometric and Doppler radar measurements of a UAV[C]//Radar Conference, 2017: 1628-1633.
|
| [6] |
Robertson D A. Millimeter-wave micro-Doppler measurements of small UAVs[C]//SPIE Defense+Security, 2017: 101880T.
|
| [7] |
Govoni M A. Micro-Doppler signal decomposition of small commercial drones[C]//Radar Conference, 2017: 425-429.
|
| [8] |
Harmanny R I A, Wit J J M D, Cabic G P. Radar micro-Doppler feature extraction using the spectrogram and the cepstrogram[C]//European Radar Conference, 2014: 165-168.
|
| [9] |
Schröder A, Murk A, Aulenbacher U, et al. Numerical RCS and micro-Doppler analysis of a consumer UAV[C]//SPIE Security+Defence, 2016: 999704.
|
| [10] |
Fuhrmann L, Biallawons O, Klare J, et al. Micro-Doppler analysis and classification of UAVs at Ka band[C]//Radar Symposium (IRS), 201718th International, 2017: 1-9.
|
| [11] |
Chen V C. The micro-Doppler effect in radar[M]. Artech House, 2011: 110-112.
|
| [12] |
陈永彬, 李少东, 杨军, 等. 旋翼叶片回波建模与闪烁现象机理分析[J]. 物理学报, 2016, 65(13): 281-291. |
| [13] |
陈永彬, 李少东, 陈文峰, 等. 直升机旋翼叶片回波建模与特性分析[J]. 空军预警学院学报, 2015, 29(5): 322-327. |
| [14] |
陈小龙, 关键, 于晓涵, 等. 基于短时稀疏时频分布的雷达目标微动特征提取及检测方法[J]. 电子与信息学报, 2017, 39(5): 1017-1023. |
| [15] |
张义安, 张冬晨, 陈卫东, 等. 基于局域波分解的机动目标ISAR成像[J]. 中国科学院研究生院学报, 2009, 26(4): 483-489. |
| [16] |
陈行勇, 刘永祥, 姜卫东, 等. 雷达目标微动分辨[J]. 系统工程与电子技术, 2007, 3(29): 361-364. |
| [17] |
黄志星.基于微多普勒的空间多目标特征提取与参数估计[D].成都: 电子科技大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10614-1015703432.htm
|
| [18] |
刘阳.微型四旋翼无人飞行器的自主起降与安全飞行研究[D].北京: 华北电力大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10079-1015642477.htm
|
 2019, Vol. 36
2019, Vol. 36 


