2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达是20世纪50年代研制出的一种主动式微波遥感设备,它不受光照和气候等客观条件的限制,能够全天时、全天候地对地面目标进行高分辨率成像,甚至可以透过植被或地表获取其掩盖的信息,适用于地面目标的检测、分类和识别等研究,已被广泛应用于遥感、军事、水文、地矿以及其他领域,具有很高的军用和民用价值[1-3]。因此,对高分辨SAR图像的解译就显得尤为重要,一直是各国研究的重点,许多国家在SAR方面的研究都取得了迅速的发展,以满足军事和民事的需求。
SAR通过脉冲压缩的方式获取距离向分辨率,通过孔径合成的方式获取方位向的分辨率。常规SAR的观测模式依赖于传感器平台的直线飞行轨迹[4],在该飞行模式下,一方面存在由于叠掩、透视伸缩等SAR影像固有的变形现象,使得SAR图像对目标观测方位向的变化十分敏感[5-6];另一方面,由于在合成孔径累积时间内雷达的观测视角范围受限,它仅能获取到观测目标在小范围方位向上的后向散射特性,而无法多方位或全方位地获取目标的散射特性,导致雷达无法完整地获取目标的信息。这给SAR图像解译和地物目标识别带来特殊难题。图 1(a)是飞行平台在不同方位向获取目标SAR图像的观测模型,图 1(b)展示飞行平台在不同方位向获取的同目标SAR图像,可以发现,即便是同一目标,飞行平台在不同方位向获取的SAR影像也各不相同。

|
Download:
|
| 图 1 多角度SAR模型和SAR图像 Fig. 1 Observation model of multi-aspect SAR and SAR images | |
传统的SAR图像目标识别方法主要对目标的单幅图像进行处理,主要目标识别方法有主成分分析(principal component analysis,PCA)方法[7]、独立成分分析(independent component analysis,ICA)方法[8]、支持向量机(support vector machine,SVM)方法[9]、非负矩阵分解(nonnegative matrix factorization,NMF)方法[10]等。也有先从单幅SAR图像中提取出多种特征并将这些特征有效地结合为一种加强特征的目标识别方法,如Huan等[11]通过PCA、ICA和Gabor变换提取出3种特征并将这3种特征并联成一种新的特征,实现SAR图像自动目标识别;Lin等[12]将图像的PCA特征和KPCA特征非线性地融合成新的特征实现SAR图像自动目标识别。近年来,深度学习被广泛应用于各个领域,并在SAR图像目标识别中取得不错的成绩:Chen和Wang[13]设计一个单隐层卷积神经网络对目标进行识别,获得90.1 %的正确识别率;Zhan等[14]设计一个拥有两级卷积+池化的神经网络架构,在经典的3类军事目标数据集上取得95.64 %的正确识别率。不过上述这些方法仅仅在目标的单一角度观测图像上提取有用信息,并没有考虑到图像数据的获取特点,没有将目标的多角度图像信息有效地结合起来,这将导致在某些方位向获取的图像可能得不到正确识别。
考虑到SAR目标对观测方位向的变化十分敏感,Brendel和Horowitz[15]首次将不同方位向观测到的多幅SAR图像用到目标识别中,并设计一个基于模板匹配的均方误差(mean square error,MSE)分类器,提高正确识别率。Huan和Pan[16]利用主成分分析方法将多角度SAR图像融合为单幅图像,并将其变换到小波域,在小波域中提取低频部分的信息作为融合图像的特征,取得不错的正确识别率。Cao等[17]针对多角度SAR图像目标识别提出基于局部自适应字典的联合稀疏表示方法,并探讨俯视角对目标正确识别率的影响。虽然以上这些方法将目标的多角度SAR图像引入到目标识别中,但没有定性地分析多角度SAR图像是如何影响目标识别率的,也没有指出需要多少幅图像就能满足识别精度的需求,对大俯视角下的目标识别探讨较少。
对此,本文设计一种利用目标多角度图像进行非相干合成的SAR目标识别性能分析方案,通过两组实验对比,探讨多角度图像给目标特征增强带来的好处,分析多角度图像对目标识别率的影响,以及多角度图像对俯视角变化的鲁棒性。首先,对多幅SAR图像进行像素级别的非相干合成处理,采用互相关系数评估策略对准图像中的目标,接着二维主成分分析(two-dimensional principal component analysis,2DPCA)算法[18]提取出非相干合成图像的特征矩阵,最后k近邻(k-nearest neighbors,k-NN)分类器[19]实现目标的分类识别。
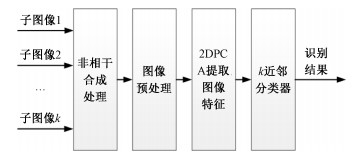
1 研究方案本文的多角度SAR图像目标识别性能分析方案共有图像非相干合成处理、预处理、特征提取和目标分类4个步骤,其处理流程如图 2所示。处理流程的输入图像是飞行平台在连续方位向上获取的同一目标的k幅SAR图像,输出则是该目标所属的类别。
|
Download:
|
| 图 2 多角度SAR目标识别流程 Fig. 2 Flow chart of multi-aspect SAR target recognition | |
为了使用图像非相干合成方法在像素级别对多幅SAR图像进行合成处理,图像中目标的朝向应尽可能地保持一致,根据目标在原始数据中的地面真实信息,将每个目标的朝向旋转到参考方位向。不妨设雷达在方位角φ获取一幅SAR图像,那么旋转后的图像可由如下旋转变换矩阵得到
| $ \left[ {\begin{array}{*{20}{c}} u\\ v \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \varphi }&{\sin \varphi }\\ { - \sin \varphi }&{\cos \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ q \end{array}} \right]. $ | (1) |
式中:(p, q)是SAR图像的原始坐标,(u, v)是变换后SAR图像的坐标。
多幅图像中的目标能否对准直接影响到非相干合成方法的处理效果,引入的互相关系数评估准则能够很好地将多幅图像中的目标对准。对于给定的在连续方位向上获取的K幅SAR图像A(k)(k=1, 2, …, K),不妨设它们的尺寸为M×N,目标所在区域的尺寸为m×n,并且它们的朝向已被修正到参考方位向,图像A(k)在(i, j)处的像素值表示为Aij(k)。目标在(i, j)处的感兴趣区域(region of interest,ROI)定义为图像中以(i, j)为中心的尺寸为m×n的一块矩形区域,表示为ROIij(k)。记第1幅SAR图像中目标的感兴趣区域ROI(1)为A(1)的中心部分,并将它作为基准ROI,简记为
| $ {\rm{RO}}{{\rm{I}}^{\left( 1 \right)}} = {\rm{ROI}}_{M/2,N/2}^{\left( 1 \right)}. $ | (2) |
接着在剩余的K-1幅图像中通过窗口滑动寻找满足公式(3)的感兴趣区域ROI(s)(s=2, 3, …, K)作为ROI(1)的最佳匹配ROI,即
| $ \begin{array}{l} {\rm{RO}}{{\rm{I}}^{\left( s \right)}} = {\rm{ROI}}_{ij}^{\left( s \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\mathop {\max }\limits_{i,j} \left( {\rho \left( {{\rm{RO}}{{\rm{I}}^{\left( 1 \right)}},{\rm{ROI}}_{ij}^{\left( s \right)}} \right)} \right), \end{array} $ | (3) |
其中
| $ \rho \left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = \frac{{{\rm{Cov}}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right)}}{{\sqrt {{\rm{Var}}\left( \mathit{\boldsymbol{X}} \right) \cdot {\rm{Var}}\left( \mathit{\boldsymbol{Y}} \right)} }}. $ | (4) |
式中:ρ(X, Y)为两个尺寸相同的感兴趣区域X、Y的互相关系数;Cov(X, Y)为它们的协方差;Var(X)为X的方差。
那么经过非相干合成处理后,SAR图像B中位于(i, j)处的像素值Bij可以表示为
| $ {\mathit{\boldsymbol{B}}_{ij}} = \mathop {\max }\limits_{s = 1,2, \cdots ,K} {\left( {{\rm{RO}}{{\rm{I}}^{\left( s \right)}}} \right)_{ij}}. $ | (5) |
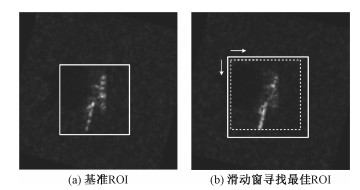
滑动窗寻找最佳ROI的示意图如图 3所示,其中图 3(a)中实线方框区域为图像的基准ROI,图 3(b)中虚线方框区域为另一幅图像的待定ROI。随着图 3(b)中的虚线方框在实线方框中滑动,计算图 3(a)的实线方框与图 3(b)的虚线方框的相关系数,其中最大相关系数对应的虚线方框即为最佳ROI。一般地,在经由目标检测算法确定后的含有目标的图像中,目标中心大致和图像中心对齐,因此,只需在图 3(b)的中心位置附近寻找最佳ROI,而无需遍历整幅图像,这大大降低了图像非相干合成阶段的时间复杂度。
|
Download:
|
| 图 3 寻找最佳ROI Fig. 3 Search for the best ROI | |
通常情况下,原始SAR图像的对比度非常巨大,图像中目标的细节不能清晰地展现出来,不符合人眼视觉系统,也不利于目标特征的提取和识别。因此,对其做一次对数变换以降低对比度显得非常有意义。
| $ {\mathit{\boldsymbol{F}}_{ij}} = 10\lg \left( {{\mathit{\boldsymbol{B}}_{ij}} + {{10}^{ - 4}}} \right) + 40. $ | (6) |
目标的不均匀散射灰度特征会对特征提取的稳定性造成干扰,因此还需对对数变换后SAR图像的幅度值作归一化处理,使图像幅度值的均值为0,方差为1。
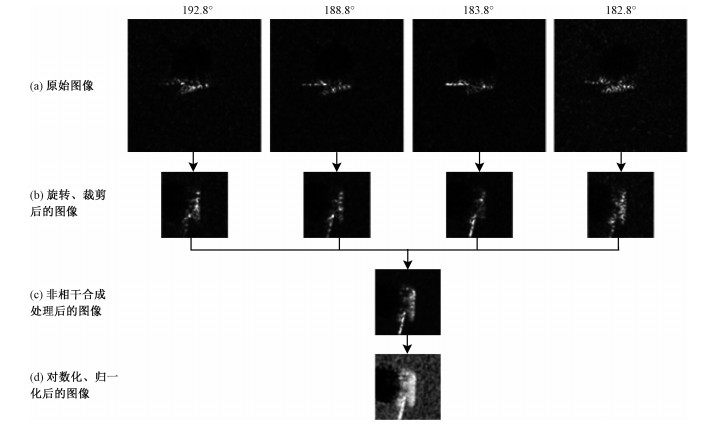
图 4示意在不同处理阶段的SAR图像。这里,选取在182.8°、183.8°、188.8°和192.8°方位向处获取的4幅SAR图像,从图 4(a)可以看出4幅图像中的目标具有大致相同的外形,但在细节上有较大的差异,且这些细节信息的空间位置分布均不一致。图 4(b)是根据目标的地面真实信息经旋转、裁剪得到的SAR图像,也即图像的ROI。图 4(c)是图像非相干合成处理后的SAR图像,与图 4(b)中的4幅图像相比,图 4(c)中目标的外形更加完整,细节信息更加丰富,这说明多角度SAR图像改善了图像质量,赋予目标更多的信息。图 4(d)是对数化、归一化之后的SAR图像,它更符合人眼视觉系统,将被用于特征提取。
|
Download:
|
| 图 4 在不同处理阶段的SAR图像 Fig. 4 SAR images at different processing stages | |
1994年,Solberg等[20]针对SAR图像质量评估引入图像清晰度的概念,也即图像的平均梯度,它反映图像中微小细节反差和纹理变换特征[21],可以用公式表示为
| $ \nabla \mathit{\boldsymbol{\bar G}} = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\sqrt {{{\left( {\partial {\mathit{\boldsymbol{G}}_{ij}}/\partial x} \right)}^2} + {{\left( {\partial {\mathit{\boldsymbol{G}}_{ij}}/\partial y} \right)}^2}} } } $ | (7) |
式中:G表示一幅图像,∂Gij/∂x表示x方向的梯度,∂Gij/∂y表示y方向的梯度。
图 5展示所用SAR图像数量对非相干合成处理效果的影响,从图中可以看出,随着图像数量的增加,合成图像的质量有了很大提升,目标与周围环境的对比更加鲜明,目标的阴影也更加清晰,阴影与目标以及周围环境的区分度更高。表 1是非相干合成所用图像数量与图像清晰度之间的定量分析,从表中可以看出,随着所用图像数量的增加,图像的清晰度值呈逐渐下降的趋势,即SAR图像中的相干斑噪声得到抑制,图像趋于平滑,目标更加突出。

|
Download:
|
| 图 5 图像数量对非相干合成效果的影响 Fig. 5 Influence of the image number on the effect of non-coherent composition | |
|
|
表 1 图像数量与图像清晰度之间的关系 Table 1 Relationship between the number of images and the definition of images |
2DPCA的核心思想是运用公式(8)将图像A投影到酉向量x上,得到投影向量y,即
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}}. $ | (8) |
令Sx为向量y的协方差矩阵,即
| $ {\mathit{\boldsymbol{S}}_x} = E\left( {\mathit{\boldsymbol{y}} - E\mathit{\boldsymbol{y}}} \right){\left( {\mathit{\boldsymbol{y}} - E\mathit{\boldsymbol{y}}} \right)^{\rm{T}}}. $ | (9) |
当tr(Sx)取得最大值时,这时候的向量x称为最优投影轴。通常情况下,我们需要一簇投影轴x1, x2, …, xd将图像A向各个方向进行投影,这样就能得到d个投影特征向量y1, y2, …, yd。所有的投影特征向量可以组成一个矩阵P=[y1, y2, …, yd],称为图像A的特征矩阵。
1.4 k近邻分类器k近邻分类器是一种基本的数据分类与回归方法,于1968年由Cover和Hart提出[22],其基本思想是利用训练数据及对特征空间进行划分,并作为其分类的“模型”。
假设训练样本集可以表示为
| $ \mathit{\boldsymbol{S}} = \left\{ {\left( {{\mathit{\boldsymbol{x}}_1},{y_1}} \right),\left( {{\mathit{\boldsymbol{x}}_2},{y_2}} \right), \cdots ,\left( {{\mathit{\boldsymbol{x}}_N},{y_N}} \right)} \right\}, $ |
式中:xi∈ Rn为第i个样本的特征向量,yi∈{c1, c2, …, cK}为第i个样本的类别,i=1, 2, …, N。
给定一个测试样本的特征向量x,计算该特征向量与S中所有训练样本的特征向量xi的距离,并找出与x最邻近的k个训练样本,将这k个训练样本装入集合Ω。接着在Ω中根据多数表决的分类策略判决x所属的类别y:
| $ y = \arg \mathop {\max }\limits_{{c_j}} \sum\limits_{{{\rm{x}}_i} \in \Omega } {\Im \left( {{y_i} = {c_j}} \right)} . $ | (10) |
式中:
在本节涉及的所有实验中,我们使用经典的静止目标获取与识别(moving and stationary target acquisition and recognition,MSTAR)数据集,并设计两个实验分别分析多角度SAR图像对目标识别正确率的改善以及对俯视角变化的鲁棒性。MSTAR数据集是1996年和1997年利用X波段、HH极化方式实测的地面静止目标数据,采用聚束式成像模式,其图像分辨率为0.3 m×0.3 m,方位向从0°~360°覆盖每个目标。在相同的俯视角下,同一目标具有190~300张在不同方位向获得的目标切片图像。
2.1 实验1实验1用到的数据为雷达在俯视角分别为15°和17°下获取到的T72坦克的SAR图像,不过这些坦克的型号各不相同,分别为A04、A05、A07、A10、A32、A62、A63和A64,这8个型号的坦克目标在同一方位向下的光学图像和SAR图像如图 6所示。从它们的光学图像来看,该8个型号的坦克具有相似的外形,只存在一些细微的差别,从它们的SAR图像来看,它们的外形几乎相同。

|
Download:
|
| 图 6 8种不同型号的T72坦克的光学图像和SAR Fig. 6 Optical images and SAR images of 8 different types of T72 tanks | |
本实验所用到的数据如表 2所示,其中在17°和15°俯视角获取的图像将分别用于训练和测试。表 3和表 4是实验1分别使用1幅和4幅图像进行识别所获得的正确识别率(probability of correct cognition,PCC)的混淆矩阵。可以发现,采用4幅图像进行识别的整体识别率比单幅图像足足提高4.52 %,各个型号坦克的识别率也均有不同程度的提升,这说明多角度SAR图像能够增强目标的特征,显著地提高目标识别率。
|
|
表 2 实验1的数据集 Table 2 Dataset of experiment ONE |
|
|
表 3 实验1的混淆矩阵(1幅图像) Table 3 Confusion matrix of experiment ONE (single image) |
|
|
表 4 实验1的混淆矩阵(4幅图像) Table 4 Confusion matrix of experiment ONE (four images) |
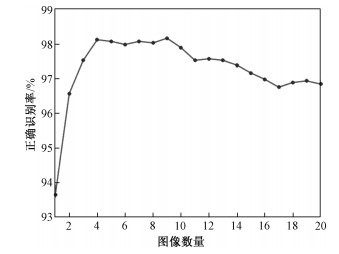
图 7是目标的正确识别率与观测图像数量之间的关系曲线图。从图中可以看出,随着非相干合成方法所用图像数量的增加,目标的正确识别率起初是急速上升,随后基本保持不变,最后缓慢下降。出现这种现象的原因是,飞行平台在目标的多个方位向对目标进行观测时,飞行平台能够获取目标在不同方位向的信息,多幅图像的非相干合成处理正是利用这些不同方位向上获取的信息,丰富目标的边缘、细节等信息,从而提高正确识别率。当所需图像数量大于一定值时,由于观测方位角度跨度较大,以至于处于两端的多幅图像之间的关联性变弱,非相干合成方法在处理时引入不必要的噪声,同时目标的阴影这一重要特性将会逐渐消失,因此降低了合成SAR图像的质量,导致识别率的下降。
|
Download:
|
| 图 7 正确识别率与图像数量的关系 Fig. 7 Relationship between PCC and the number of images | |
实验2使用的数据为雷达在俯视角分别为15°、17°、30°和45°下获取的3类军事目标的SAR图像,这3类目标分别为2S1、BRDM2和ZSU23/4,它们在同一方位向、不同俯视角下的SAR图像如图 8所示。从图中可以发现,随着俯视角差异的增大,目标的形态变化非常巨大,越来越偏离目标自身固有的形态,这给SAR图像目标识别带来挑战性的难题。

|
Download:
|
| 图 8 3类军事目标在不同俯视角下的光学图像及其SAR图像 Fig. 8 Optical and SAR images of 3 kinds of military targets at different depression angles | |
本实验所用的数据如表 5所示,其中在17°俯视角下获取的SAR图像将用于训练,在15°、30°和45°俯视角下获取的SAR图像将用于测试,共有2S1、BRDM2和ZSU23/4这3类目标。
|
|
表 5 实验2的数据集 Table 5 Dataset of experiment TWO |
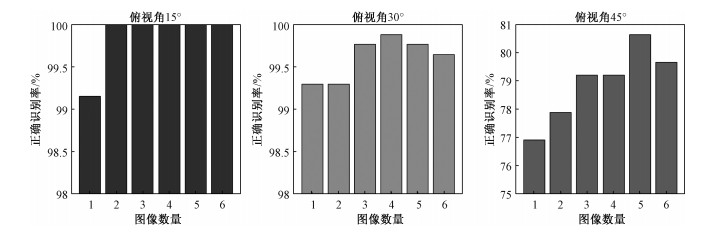
以17°俯视角下的图像样本为训练集,15°、30°、45°俯视角下的图像样本为测试集,所用图像数量与正确识别率之间的关系如图 9所示。从图中可以看出,随着图像数量的增加,目标在15°、30°、45°俯视角下的正确识别率都有提升,这说明多角度观测SAR确实能够提高目标识别率。特别地,当俯视角为15°时,仅使用2幅图像就能达到100 %的识别率;当俯视角为30°时,需用4幅图像才能达到最高的识别率;而当俯视角为45°时,需用5幅图像才能达到最高的识别率。由此可见,随着俯视角度差异的增大,为提高目标的正确识别率,所需图像数量也有所增加。从最高识别率来看,俯视角差异的增加导致识别率的降低,说明俯视角的变化会给目标识别带来一定的困难,目标对俯视角的变化也较敏感。在俯视角为30°和45°时,可以分别达到99.88 %和80.64 %的正确识别率,说明多角度SAR图像对俯视角的变化具有较强的鲁棒性。
|
Download:
|
| 图 9 不同俯视角下,正确识别率与图像数量之间的关系 Fig. 9 Relationship between PCC and the number of images at different depression angles | |
表 6是在15°、30°和45°俯视角的条件下本文方法的识别率与其他方法的比较。可以看出,当测试集数据的俯视角与训练集相差较小(15°俯视角)时,该表列举的所有方法均能获得非常不错的正确识别率,且本文方法能达到100 %的识别率;但是当俯视角相差较大(30°俯视角)时,所有方法的识别率均呈现出不同程度的下降,其中以JSR和子字典方法下降得最为严重,而本文方法的识别率几乎不受影响;当俯视角相差很大(45°俯视角)时,所有方法的识别率下降得更为厉害,而本文方法却能达到80.64 %的识别率,这说明与其他方法相比,本文方法对俯视角的变化具有更高的鲁棒性。
|
|
表 6 与其他方法的PCC对比 Table 6 PCC comparison with other methods |
本文设计一种利用目标多方位向图像进行非相干合成的SAR目标识别性能分析方案,定量地分析多角度SAR图像给目标特征带来的好处,及多角度SAR图像的识别性能与所用图像数量的关系,最后分析多角度SAR图像对俯视角变化的鲁棒性情况。实验结果表明,多角度SAR图像能够增加目标的信息量,增强目标的特征;与单幅SAR图像相比,多角度SAR图像能够显著提升目标的识别性能,但所用图像数量并不是越多越好,过多的图像反而会导致识别性能的下降;多角度SAR图像对俯视角差异的变化具有较强的鲁棒性,能获得较高的正确识别率。
| [1] |
盖旭刚, 陈晋汶, 韩俊, 等. 合成孔径雷达的现状与发展趋势[J]. 飞航导弹, 2011(3): 82-86. |
| [2] |
张红. 高分辨率SAR图像目标识别[M]. 北京: 科学出版社, 2009.
|
| [3] |
Moreira A, Prats-Iraola P, Younis M, et al. A tutorial on synthetic aperture radar[J]. IEEE Geoscience & Remote Sensing Magazine, 2013, 1(1): 6-43. |
| [4] |
洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135. |
| [5] |
向卫力, 李晓辉, 周勇胜, 等. 一种鲁棒的多尺度稀疏表示SAR目标识别方法[J]. 中国科学院大学学报, 2017, 34(1): 99-105. |
| [6] |
O'Sullivan J A, Devore M D, Kedia V, et al. SAR ATR performance using a conditionally Gaussian model[J]. IEEE Transactions on Aerospace & Electronic Systems, 2001, 37(1): 91-108. |
| [7] |
He Z, Lu J, Kuang G. A fast SAR target recognition approach using PCA features[C]//International Conference on Image and Graphics. Sichuan: IEEE, 2007: 580-585.
|
| [8] |
Tao M, Zhou F, Liu Y, et al. Tensorial independent component analysis-based feature extraction for polarimetric SAR data classification[J]. IEEE Transactions on Geoscience & Remote Sensing, 2015, 53(5): 2481-2495. |
| [9] |
Anagnostopoulos G C. SVM-based target recognition from synthetic aperture radar images using target region outline descriptors[J]. Nonlinear Analysis, 2009, 71(12): 2934-2939. DOI:10.1016/j.na.2009.07.030 |
| [10] |
Cui Z, Cao Z, Yang J, et al. SAR target recognition using nonnegative matrix factorization with L1/2 constraint[C]//Radar Conference. Cincinnati: IEEE, 2014: 382-386.
|
| [11] |
Huan R H, Zhang P, Pan Y. SAR target recognition using PCA, ICA and Gabor wavelet decision fusion[J]. Journal of Remote Sensing, 2012, 16(2): 262-274. |
| [12] |
Lin C, Peng F, Wang B H, et al. Research on PCA and KPCA self-fusion based MSTAR SAR automatic target recognition algorithm[J]. Journal of Electronic Science and Technology, 2012, 10(4): 352-357. |
| [13] |
Chen S, Wang H. SAR target recognition based on deep learning[C]//International Conference on Data Science and Advanced Analytics. IEEE, 2015: 541-547.
|
| [14] |
Zhan R H, Tian Z Z, Hu J M, et al. SAR automatic target recognition based on deep convolutional neural network[C]//2016 International Conference on Artificial Intelligence: Techniques and Applications. AITA, 2016: 170-178.
|
| [15] |
Brendel G F, Horowitz L L. Benefits of aspect diversity for SAR ATR: fundamental and experimental results[C]//Algorithms for Synthetic Aperture Radar Imagery VⅡ. SPIE, 2000: 567-578.
|
| [16] |
Huan R H, Pan Y. Target recognition for multi-aspect SAR images with fusion strategies[J]. Progress in Electromagnetics Research, 2013, 134(1): 267-288. |
| [17] |
Cao Z J, Xu L Y, Feng J L. Automatic target recognition with joint sparse representation of heterogeneous multi-view SAR images over a locally adaptive dictionary[J]. Signal Processing, 2016, 126(1): 27-34. |
| [18] |
Yang J, Zhang D, Frangi A F, et al. Two-dimensional PCA:a new approach to appearance-based face representation and recognition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(1): 131-137. |
| [19] |
Cover T, Hart P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967, 13(1): 21-27. DOI:10.1109/TIT.1967.1053964 |
| [20] |
Solberg A H S, Jain A K, Taxt T. Multisource classification of remotely sensed data:fusion of Landsat TM and SAR images[J]. IEEE Transactions on Geoscience & Remote Sensing, 1994, 32(4): 768-778. |
| [21] |
阳方林, 郭红阳, 杨风暴. 像素级图像融合效果的评价方法研究[J]. 测试技术学报, 2002, 16(4): 276-279. DOI:10.3969/j.issn.1671-7449.2002.04.014 |
| [22] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
|
| [23] |
Amoon M, Rezai-Rad G A. Automatic target recognition of synthetic aperture radar (SAR) images based on optimal selection of Zernike moments features[J]. Computer Vision IET, 2013, 8(2): 77-85. |
| [24] |
Dong G, Kuang G. Classification on the monogenic scale space:application to target recognition in SAR image[J]. IEEE Transactions on Image Processing, 2015, 24(8): 2527-2539. DOI:10.1109/TIP.2015.2421440 |
| [25] |
Anagnostopoulos G C. SVM-based target recognition from synthetic aperture radar images using target region outline descriptors[J]. Nonlinear Analysis, 2009, 71(12): 2934-2939. DOI:10.1016/j.na.2009.07.030 |
| [26] |
Mishra A K. Validation of PCA and LDA for SAR ATR[C]//2008 IEEE Region 10 Conference. Hyderabad: IEEE, 2009: 1-6.
|
| [27] |
Cui Z Y, Cao Z J, Yang J Y. Target recognition in synthetic aperture radar images via non-negative matrix factorization[J]. IET Radar Sonar & Navigation, 2015, 9(9): 1376-1385. |
| [28] |
Zhang H, Nasrabadi N M, Zhang Y, et al. Multi-view automatic target recognition using joint sparse representation[J]. Aerospace & Electronic Systems IEEE Transactions, 2012, 48(3): 2481-2497. |
 2019, Vol. 36
2019, Vol. 36 


