热电制冷又称温差电制冷或半导体制冷。热电制冷有结构简单、无机械运动部件、无制冷剂、控制精度高等优点,广泛应用于国防、医疗、科研、通信、航海、农业、动力及工业生产等领域,但由于热电制冷器的效率较低、加工制造工艺较复杂,限制了它的推广和应用[1-3]。目前,研究人员在理论模拟、热电材料、温差电对结构等方面做了大量研究工作,取得很大成果,其中理论方面的研究已达到相对成熟的程度[4]。因此,目前热电制冷的研究方向主要在热电材料、温差电对结构及冷热端强化散热方式[5]等。在热电材料方向,前苏联约飞院士发现掺杂的半导体材料有良好的发电和制冷性能[6]后,推动了研究者在此领域的研究热潮。现有热电器件的转化率可达10%,与传统压缩机的制冷效率还有很大差距[7]。但当热电材料的性能足够好时,其效率可无限接近卡诺循环效率,因此探索新型的热电材料、提高现有材料的热电性能是现有热电材料领域的研究热点[8]。在温差电对结构设计方面,可以通过优化设计半导体制冷模块,减小半导体制冷模块的理想性能系数和实际性能系数间的差值,提高半导体制冷器的实际制冷性能[9]。
现有的强化散热方式主要有:自然对流散热、强迫对流散热、水冷散热、相变沸腾换热等[10]。李茂德和卢希红[11]用热电制冷性能与热端散热强度之间的微分方程,在第三类边界条件下得到热电制冷性能与热端散热强度之间的关系。任欣和张鹏[12]给出热电制冷器在有限的热端散热强度下不同制冷工况的实验研究,并推导出最佳工况下热电制冷器的工作电流和制冷量的近似公式。金刚善等[13]研究小空间中,散热器和散冷器的结构对热电制冷效率的影响。简弃非等[14]研究制冷空间温度在冷端自然对流和强制对流状态下随时间变化的规律。而散热强度对于热电制冷性能影响的实验,现有文献报道较少;且散冷强度对于热电制冷性能影响的研究也处于薄弱环节。
本文拟通过实验的方式,研究并验证散热强度、散冷强度对热电制冷性能和制冷空间温度的影响。
1 热电制冷原理热电制冷是基于热电效应的应用,主要是帕尔帖效应在制冷技术方面的应用。使用的热电制冷装置是由热电效应比较显著、热电效应效率比较高的半导体热电偶构成的。
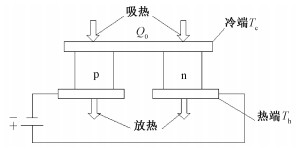
如利用一只p型半导体元件和一个n型半导体元件联结成热电偶,接上直流电源后,在接头处就会产生温差和热量的转移。在上端面一个接头处,电流方向是n→p,温度下降并且吸热,即为冷端。在下端面一个接头处,电流方向是p→n,温度上升并且放热,此为热端。其流程详见图 1。
|
Download:
|
| 图 1 热电制冷原理图 Fig. 1 Schematic diagram of thermoelectric refrigerator | |
在热电偶通上电流后,交接面附近在1 s内放出或吸收的热量Qp(帕尔帖热)。如果在放热的接头上提前做好散热措施,使它保持一定的温度Th,则另一接头开始冷却。直到从周围介质传入这个接头的热量Q0和沿着电偶臂传入的热量Qhc的总和等于所吸收的帕尔帖热量Qp时,即
| $ {{Q}_{\text{p}}}={{Q}_{0}}+{{Q}_{\text{hc}}}, $ | (1) |
此时冷接头的温度达到平衡,温度为Tc。
制冷工况下,热电制冷器冷端从被冷介质吸收的热量称为产冷量,产冷量的表达式为
| $ {{Q}_{0}}={{Q}_{\text{p}}}-{{Q}_{\text{hc}}}. $ | (2) |
热端放出热量Qh的表达式为
| $ {{Q}_{\text{h}}}={{Q}_{0}}+\omega , $ | (3) |
式中ω为制冷过程中所消耗的电功率。
热电制冷器热端冷却所需的热量,和其他形式的制冷机一样,等于有效产冷量与所消耗的电功率之和[15]。若热端面的温度无法稳定,则冷端无法持续制冷,即使初始产生制冷效果,随后也会随着热端温度的上升被Qhc抵消,从而变成放热源,导致制冷量下降。当热端散热能力增强,热电制冷器的输入功率不变时,Q0会增大,即制冷量增加。所以解决好热电制冷器的散热问题对制冷效率的提高起到至关重要的作用[16]。
2 实验及测量系统 2.1 实验系统实验的目的是测试得到不同散热强度和散冷强度下热电制冷的散热器和散冷器的耦合温度曲线,以及获得制冷空间不同测点温度曲线;最终得到热端强制对流与冷端强制对流对热电制冷性能及制冷空间温度分布的影响规律。
本次实验采用的热电制冷器是TEC1-12706,具体参数见表 1。
|
|
表 1 TEC1-12706参数表 Table 1 Parameter table for TEC1-12706 |
热电制冷器两端分别连接一个肋片型散热器,一个用于散热,一个用于散冷(在本文中分别称为散热器和散冷器)。本实验所用散热器和散冷器的相关尺寸见表 2。
|
|
表 2 散热器和散冷器参数表 Table 2 Parameter table for radiators and coolers |
在热电制冷器两端抹导热硅胶,以减少接触热阻,并使接触面平滑充分接触。在散热器和散冷器之间、热电制冷器四周填充隔热垫片,以减少散热器和散冷器之间的传热,并防止在组装的过程中将热电制冷器压坏。散热器端和散冷器端外侧各有一个小风扇,分别称为散热风扇和散冷风扇,其相关参数见表 3。
|
|
表 3 散热风扇和散冷风扇参数表 Table 3 Parameter table for radiator fan and cooler fan |
制冷空间采用的是泡沫箱,泡沫箱能起到一定的保温隔热作用,且壁面易打孔;既满足实验需求,也方便实验操作。其相关尺寸见表 4。
|
|
表 4 制冷空间尺寸 Table 4 Cooling space size |
泡沫箱顶部开有40 mm×45 mm的开口用于安装热电制冷器的散冷器,整个实验系统外观如图 2所示。

|
Download:
|
| 图 2 实验系统外观图 Fig. 2 Experimental system appearance | |
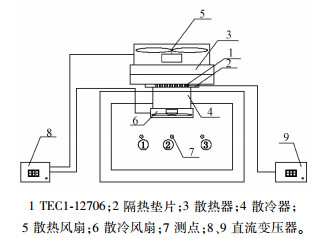
实验所用泡沫箱内的测点布置在箱顶正中间轴线上,从箱体一侧面正中间开孔,在轴线上依次布置测点1~3号,每个测点间的间距为36 mm,测点分布见图 3。制冷空间的温度和肋片温度都用铜-康铜热电偶测量,通过Agilent34972A仪器进行数据采集,在进行实验数据测量之前,用水银温度计对其进行标定,本实验标定所用水银温度的精度为0.1 ℃,所以本实验传感器的精度为0.1 ℃,故实验数据保留小数点后2位。
|
Download:
|
| 图 3 实验系统流程图 Fig. 3 Flow chart of experimental system | |
为研究并验证散热强度、散冷强度对热电制冷性能和制冷空间温度的影响,本次实验分为3组:第1组是研究散热器自然对流和强制对流对热电制冷性能和制冷空间温度的影响。第2组是研究散热强度对热电制冷性能和制冷空间温度的影响。第3组是研究散冷器自然对流和强制对流对热电制冷性能和制冷空间温度的影响。3组实验输入条件见表 5。
|
|
表 5 3组实验输入条件 Table 5 Three sets of experimental input conditions |
由于不同工况的实验是在不同时刻进行的,散热环境温度是不同的,所以温度曲线的初始值不同,为便于分析以及消除室外环境的影响,本文温度曲线图中的所有温度值都是实测值与其对应的散热环境温度值的差值(在本文中均定义为相对温度),每组实验对应的散热环境温度见表 5。
4 实验结果与分析 4.1 散热器自然对流和强制对流对比试验由图 4(a)可知,散热器强制对流散热可改变热电制冷性能。冷热端均为自然对流散热时,散热器的相对温度随时间持续上升,散冷器的相对温度先下降到最低值然后上升,且在实验进行到600 s时,散热器的相对温度为26.05 ℃,散冷器的相对温度为-3.97 ℃。散热器端强制对流散热时,散热器的相对温度先上升到3.20 ℃后稳定,散冷器的相对温度先下降到-20.00 ℃后稳定。

|
Download:
|
| 图 4 散热器自然对流和强制对流工况相对温度曲线图 Fig. 4 Relative temperature curves of radiators under natural convection and forced convection | |
增强散热强度能够提高热电制冷性能。由公式(3)可知,强制对流强化了热端散热,散热量增加,输入功率不变,热电制冷性能提高。实际工程中,需要保证热端散热量满足热电制冷器的散热需求,才能实现热电制冷器持续稳定的工作。
由图 4(b)可知,在冷热端均为自然对流的工况下散热器与散冷器的温差最终维持在30 ℃左右;在散热器端强制对流的工况下散热器与散冷器的温差最终维持在24 ℃左右。
增强散热强度,散热器和散冷器温差会减小。热端散热器强制对流散热,使热端热量(帕尔帖热、焦耳热、传导热)迅速传递出去,防止热量堆积,散热器温度持续升高;热端散热器自然对流时,热量堆积无法迅速传递出去,使更多的热量流向冷端。因此,热端强制对流散热时,散热器和散冷器温差小。实际工程应用中,应采取合理的措施加快热端热量散出,避免热量堆积造成热电制冷无法实现。
由图 5可知,制冷空间内3个温度测点的相对温度曲线中测点1和测点2的相对温度值比较接近,测点3相对温度与测点1和测点2的相对温度相比都偏高,这是由于在测点3这一侧的侧壁上开洞布置3个测点的铜-康铜热电偶线,洞口处内外有温差形成对流,外部的热空气会进入内部,使测点3的相对温度略高于其他两个测点的相对温度。

|
Download:
|
| 图 5 不同散热器工况下散冷器与制冷空间相对温度分布曲线 Fig. 5 Relative temperature curves of the cooler and the cooling space under the different heat dissipation situations | |
冷热端均为自然对流工况下,制冷空间相对温度与散冷器相对温度温差最大达到7 ℃左右(图 5(a))。散热器端强制对流工况下,制冷空间相对温度与散冷器相对温度温差最大达到14 ℃左右(图 5(b))。散冷器端为自然对流时,制冷空间与散冷器的温差偏大(与4.3节中的实验数据相比),不能充分利用热电制冷器产生的冷量,造成能源浪费,降低热电制冷器的效率。
散热器强制对流和自然对流工况下,制冷空间相对温度曲线的变化趋势都与相应工况下的散冷器相对温度曲线变化趋势一致。增强散热强度能够快速降低并稳定散冷器的相对温度,散冷器与制冷空间空气自然对流换热,使制冷空间的相对温度值维持在略低于初始相对温度的值,但与散冷器相对温度的稳定值相差较大。散热器强制对流强度的变化,对制冷空间温度基本无影响,仅能实现散冷器温度的改变。
4.2 散热器不同散热强度对比试验在进行散热器不同散热强度对比试验前,先对散热强度进行定量,即通过改变散热风扇输入电压实现散热强度的改变。实验中,散热风扇分别在输入电压为5、7、9、11和12 V时,测量得到散热强度对应的风量值。其结果如表 6所示。
|
|
表 6 不同电压下散热风扇风量 Table 6 Air volumes of radiator fan at different voltage values |
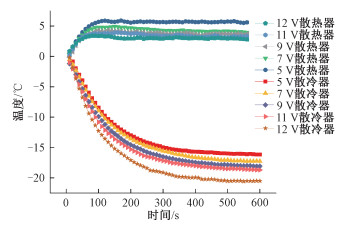
图 6是散热强度依次为表 6中各实验条件时,各自所对应的散热器和散冷器相对温度曲线。
|
Download:
|
| 图 6 不同散热强度下散热器和散冷器相对温度曲线 Fig. 6 Relative temperature curves of radiator and cooler under different heat dissipation strengths | |
由图 6可知,由于热电制冷器散热器和散冷器的温度呈耦合变化规律,因此热电制冷器输入电压为定值(即输入电压为7 V)时,散热强度(在19.05~37.96 m3/h范围内)的增加,有利于提高热电制冷性能,散热器和散冷器温相对温度均逐渐降低。散热风量影响热电制冷器性能的机理是散热风量所带走的热量和热电制冷器需要带走的热量之间的相对大小,散热风量带走的热量大于所需要带走的热量,会使散热器和散冷器温度降低,从而提高热电制冷性能。
给定的热电制冷器,在确定的输入条件下,热电制冷性能与散热强度成正比,但热电制冷性能增加伴随着散热风扇输入功率的消耗,所以存在最佳散热风量,使得散热风扇和热电制冷器的输入功耗和为极小值,从而实现热电制冷器制冷性能最佳。代伟[17]在分析第3类边界条件下热电制冷性能与热端散热强度之间的微分方程进行数值计算所得的曲线时和赵亮等[18]在研究热端液体散热工况下热电制冷器功率与散热性能间的关系时,得到了与此相同的结论。实际工程中,热端散热方式及散热量的选取确定,既要满足热电制冷器实际工作环境的需要,也要考虑经济效益最优。
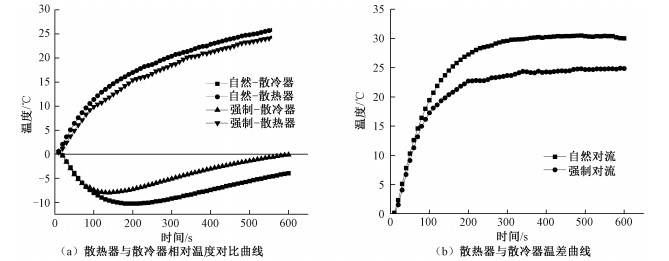
4.3 散冷器自然对流和强制对流对比试验由图 7(a)可知,散冷风扇不能改变散热器和散冷器相对温度曲线趋势。有无散冷风扇,散热器的相对温度均随着时间持续上升,散冷器的相对温度均先下降到最低值,然后持续上升,散冷风扇对热电制冷性能无作用。
|
Download:
|
| 图 7 散冷器自然对流和强制对流工况相对温度曲线图 Fig. 7 Relative temperature curves of a cooler under natural convection and forced convection | |
由公式(1)可知,当散热器端的散热无法满足热电制冷器需求时,热端温度无法稳定,冷端则无法实现稳定制冷。即使冷热端仍能实现热交换,散热器因为热量Qh的堆积,热量无法快速散出导致热端温度持续升高;散冷器则因为Qhc随着冷热端温差增大而增大,致使Q0随着温差增大而减小,直至冷端不再吸热变成放热。在实际应用中,一定要保证热端散热量满足热电制冷器的需求,否则热电制冷器将无法持续稳定工作,且经过一段时间的热量积累将会烧坏热电制冷器。
由图 7(b)可知,在冷热端均为自然对流的工况时散热器与散冷器的温差最终维持在30 ℃左右;在散冷器端强制对流的工况时散热器与散冷器的温差最终维持在24 ℃左右。
散冷器端散冷强度增强也会使散热器和散冷器的温差减小。散冷器端散冷风扇工作,实现周围空气与其循环换热,温度升高,因此散冷器和散热器温差减小。
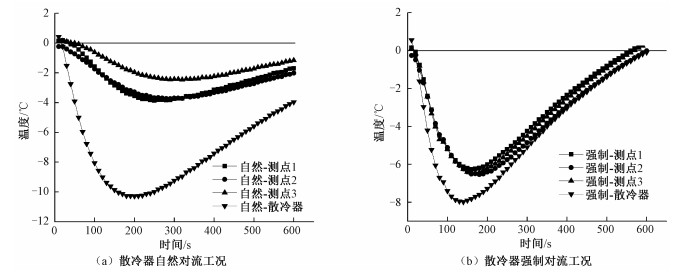
由图 8可知,冷热端均为自然对流工况下和热端自然对流、冷端强制对流工况下,制冷空间相对温度曲线的变化趋势都与对应工况下的散冷器相对温度曲线变化趋势一致。
|
Download:
|
| 图 8 不同散冷器工况下散冷器与制冷空间相对温度分布曲线 Fig. 8 Relative temperature curves of the cooler and cooling space under the different cooling situations | |
冷热端均为自然对流工况时,制冷空间与散冷器最大温差达7 ℃左右。散冷器端强制对流工况时,制冷空间与散冷器最大温差达2 ℃左右。
在强制对流作用下,散冷器散发的冷量得以迅速传递到制冷空间,空气温度与散冷器温度差较小,可充分利用热电制冷器产生的冷量。实际工程中,需要加强散冷器与制冷空间的强化换热,才能保证充分利用热电制冷器的冷量及制冷空间温度分布的均匀性。
增强散冷强度不能使制冷空间的温度稳定,会使制冷空间温度随着散冷器温度波动,制冷过程中,制冷空间温度与散冷器始终保持较小温差。
5 结论1) 给定的热电制冷器,在确定的输入条件下,热端强制对流能满足散热需求,实现持续稳定制冷,而自然对流无法实现。在本实验条件下,热端自然对流时,制冷空间无法实现持续稳定的制冷效果;在实验时间内散热器相对温度由初始的0 ℃持续上升至26.05 ℃;散冷器的相对温度由0 ℃先降至-10.29 ℃,而后开始持续上升,到600 s时相对温度上升至-3.97 ℃。热端强制对流最终将散热器和散冷器的相对温度分别稳定在3.20和-20.00 ℃。
2) 给定的热电制冷器,在确定的输入条件下,热电制冷性能与散热强度成正比,但热电制冷性能增加伴随着散热风扇功率的消耗,所以在满足制冷空间控制温度需求的情况下,存在最佳散热风量,使得散热风扇和热电制冷的输入功耗和为极小值,此时热电制冷器的综合能效最佳。
3) 给定的热电制冷器,在确定的输入条件下,冷端强制对流相对自然对流加快了散冷器与制冷空间空气热交换,减小了散冷器与制冷空间温差。在本实验条件下,冷端自然对流时,散冷器与制冷空间最大温差达7 ℃,而强制对流可减小至2 ℃。
| [1] |
朱倩, 刘玉超, 张强, 等. 半导体制冷技术及其应用[J]. 学园:教育科研, 2011(2): 31. |
| [2] |
李冰. 半导体制冷技术及其发展[J]. 山西科技, 2009(4): 95. DOI:10.3969/j.issn.1004-6429.2009.04.049 |
| [3] |
谢玲, 汤广发. 半导体制冷技术的发展与应用[J]. 洁净与空调技术, 2008(1): 68-71. DOI:10.3969/j.issn.1005-3298.2008.01.018 |
| [4] |
张婷婷, 王亚雄, 段建国. 热电制冷技术研究进展[J]. 化学工程与装备, 2017(7): 226-228. |
| [5] |
胡韩莹, 朱冬生. 热电制冷技术的研究进展与评述[J]. 制冷学报, 2008, 29(5): 1-7. DOI:10.3969/j.issn.0253-4339.2008.05.001 |
| [6] |
张文杰.热电器件的热弹性应力分析及外加电、磁场环境下的性能测试[D].兰州: 兰州大学, 2010.
|
| [7] |
Rogl G, Grytsiv A, Rogl P, et al. n-Type skutterudites (R, Ba, Yb)(y)Co4Sb12(R=Sr, La, Mm, DD, SrMm, SrDD) approaching ZT approximate to 2.0[J]. Acta Materialia, 2014, 63: 30-43. DOI:10.1016/j.actamat.2013.09.039 |
| [8] |
Puneet P, Podila R, Karakaya M, et al. Preferential scattering by interfacial charged defects for enhanced thermoelectric performance in few-layered n-type Bi2Te3[J]. Scientific Reports, 2013, 3(11): 3212. |
| [9] |
杨建敏.风冷散热半导体制冷系统性能分析及实验研究[D].南昌: 南昌大学, 2009.
|
| [10] |
贾艳婷, 徐昌贵, 闫献国, 等. 半导体制冷研究综述[J]. 制冷, 2012, 31(1): 49-55. |
| [11] |
李茂德, 卢希红. 热电制冷过程中散热强度对制冷参数的影响分析[J]. 同济大学学报(自然科学版), 2002, 30(7): 811-813. DOI:10.3321/j.issn:0253-374X.2002.07.007 |
| [12] |
任欣, 张鹏. 有限散热强度下半导体制冷器性能的实验研究[J]. 低温工程, 2003(4): 57-62. DOI:10.3969/j.issn.1000-6516.2003.04.009 |
| [13] |
金刚善, 李彦, 刁永发. 小空间半导体制冷的实验研究[J]. 兰州理工大学学报, 2004, 30(3): 51-54. DOI:10.3969/j.issn.1673-5196.2004.03.015 |
| [14] |
简弃非, 梁荣光, 张勇, 等. 半导体制冷效率及空间冷量传递特性试验研究[J]. 华南理工大学学报(自然科学版), 2001, 29(5): 72-75. DOI:10.3321/j.issn:1000-565X.2001.05.018 |
| [15] |
徐德胜. 半导体制冷与应用技术[M]. 上海: 上海交通大学出版社, 1992.
|
| [16] |
白晓亮. 半导体制冷的散热与热管散热器的设计[J]. 制冷, 1998(4): 46-49. |
| [17] |
代伟. 半导体制冷散热强度对制冷性能的影响[J]. 制冷与空调, 2008, 22(3): 25-27. DOI:10.3969/j.issn.1671-6612.2008.03.005 |
| [18] |
赵亮, 张丰华, 杨明明, 等. 热电制冷器散热性能实验研究[J]. 机械研究与应用, 2016, 29(3): 123-124. |
 2019, Vol. 36
2019, Vol. 36 


