2. Key Laboratory of Big Data Mining and Knowledge Management of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Information and Communication, Wuhan College, Wuhan 430212, China
2. 中国科学院大数据挖掘与知识管理重点实验室, 北京 100049;
3. 武汉学院信息系, 武汉 430212
Multiple outcomes comparison is frequently encountered in many research areas. For example, in a plasma-renin activity clinical trail[1-2], investigators aimed to see whether the drug fenoterol increases or reduces plasma-renin activity, five endpoints described by five occasions (after 0, 2, 6, 8, and 12 h) were measured. In genetics, in order to see whether the genetic variants increase the risk of disease occurrence, investigators often collect two groups of individuals with the case group suffering from disease and the control group being healthy, and many outcomes described by genetic variants are genotyped on them. In genomics, to investigate the age-dependent regulation of gene expression in human brain, RNAs harvested from postmortem samples of 30 individuals were analyzed using Affymetrix gene chips and the aim was to see whether the gene expression patterns varied among two groups categorized by age of 73 with adjusting for gender[3].
Many procedures including parametric and nonparametric ones have been developed in the literature. A classic method is the Hotelling's T2 test (HT)[4], which is the optimal invariant test when data follow multinormal distribution with homoscedasticity. If the normal assumption is violated, the non-parametric methods are rank-sum test (RST)[5], adjusted rank-sum test (ARST)[6], and rank-maximum test (MAX)[7]. The above tests were derived without adjusting for covariates. However, in a real application such as the ageing human brain data[3] analyzed later, the investigators want to see the differences of multiple patterns between cases and controls after adjusting for gender. At this point, covariate adjustment is essential, and it reduces the bias and improves the precision of the comparison(see Refs.[8-12]).
In this work, we combine a version of ARST and the pseudo F test, which was developed to handle the ecologic data in Ref.[13] and can be thought as a non-parametric version of multivariate regression model[14-17], and propose a MIN2 test.
1 The MIN2 testConsider two groups, group 1 and group 2. Suppose that there are n1 and n2 subjects sampled from the two groups, respectively, and k(k>1) outcomes are measured on a continuous scale on each individual. Let n=n1+n2, Y1 and X1 be the response and covariate matrices for group 1, with dimension of n1×k and n1×d, respectively, and Y2 and X2 be the response and covariate matrices for group 2, with dimension of n2×k and n2×d, respectively. Define
H0:There is no difference between the two groups after covariate adjustment.
When considering the covariates, the HT, RST, ARST, and MAX can not be applied directly. So we project Y orthogonal to the space spanned by covariates X to get the residual matrix E, that is,
| $ \mathit{\boldsymbol{E = }}\left( {{\mathit{\boldsymbol{I}}_n} - {\mathit{\boldsymbol{H}}_X}} \right)\mathit{\boldsymbol{Y}} = \left( \begin{array}{l} {\mathit{\boldsymbol{E}}_1}\\ {\mathit{\boldsymbol{E}}_2} \end{array} \right), $ |
where In is n-dimensional identity matrix, HX=X(XτX)-1Xτ, E1 and E2 are matrices with dimension of n1×k and n2×k, respectively. Denote E=(euv), u=1, 2, …, n, and v=1, 2, …, k. The marginal distributions corresponding to e1v and env are Fv and Gv, respectively. At this point, the tests such as HT, RST, ARST, and MAX mentioned above can be obtained based on E.
The ARST was proposed in Ref.[6] to accommodate the null hypothesis
| $ {T_h} = \frac{{{{\bar R}_2} - {{\bar R}_1}}}{{\widehat \sigma \sqrt {\widehat h\left( {1/{n_1} + 1/{n_2}} \right)} }}, $ | (1) |
where
| $ h = \frac{{\sum\limits_{u = 1}^k {\sum\limits_{v = 1}^k {{{\left( {1 + \lambda } \right)}^2}\left( {{a_{uv}} + {b_{uv}}\lambda } \right)} } }}{{\sum\limits_{u = 1}^k {\sum\limits_{v = 1}^k {\left[ {{e_{uv}}{\lambda ^3} + \left( {{b_{uv}} + 2{f_{uv}}} \right){\lambda ^2} + \left( {{a_{uv}} + 2{q_{uv}}} \right)\lambda + {p_{uv}}} \right]} } }}, $ |
where
au v=cov(Gu(e1 u), Gv(e1 v)), bu v=cov(Fu(en u), Fv(en v)), eu v=cov(Fu(e1 u), Fv(e1 v)), fu v=cov(Fu(e1 u), Gv(en v)), pu v=cov(Gu(en u), Gv(en v)), quv=cov(Gu(en u), Fv(e1 v)), and λ=n1/n2.
The ARST maintains good power in the alternative parameter space when θvs lie in the same direction. When θvs lie in different directions or the magnitudes of some of θvs are large, the test may suffer from substantial loss of power. So, a MAX test was proposed in Ref.[7] to address this issue. However its power is not optimistic when most of the endpoints provide evidences and these evidences are not so strong.
When θvs lie in different directions or the magnitudes of some of θvs are large, the Kendall τ distance is applied in identifying this difference very well. The Kendall τ distance between two groups of observations is defined as the total number of discordant pairs. The larger the distance, the more dissimilar both groups are. Let D=(dlm)n×n be the Kendall τ distance matrix based on Y and S=(slm)n×n with slm=
| $ {T_F} = \frac{{{\rm{tr}}\left[ {\left( {{\mathit{\boldsymbol{H}}_Z} - {\mathit{\boldsymbol{H}}_X}} \right)\mathit{\boldsymbol{CSC}}} \right]}}{{{\rm{tr}}\left[ {\left( {{\mathit{\boldsymbol{I}}_n} - {\mathit{\boldsymbol{H}}_Z}} \right)\mathit{\boldsymbol{CSC}}} \right]}}. $ | (2) |
Let p1 be the p-value of Th and p2 be the p-value of TF, where p1 can be obtained by the normal distribution and p2 is obtained by permutation procedure [14]. We propose an MIN2 as
| $ {\rm{MIN2 = min}}\left( {{p_1}, {p_2}} \right). $ | (3) |
The MIN2 test integrates the superiorities of Th and TF and is thus more robust than Th and TF. However, the asymptotical distribution of MIN2 is not known. We recommend to use the permutation procedure to get the p-value of MIN2:
1) set a large number B, for example B=1 000, and calculate the MIN2 statictic using the observations, denote it by η(0);
2) for b from 1 to B, randomly permute n observations and arrange the first n1 samples to group 1 and other n2 samples to group 2, and calculate the MIN2 statictic, denote it by η(b);
3) the p-value of the MIN2 statictic is calculated as
We conduct simulation studies to evaluate the performance of the proposed MIN2 with HT, RST, ARST, and MAX. The empirical type Ⅰ error rates and powers are simulated using data from two distributions: Log-normal and Laplace distributions. To study the influence of small sample size, we consider n1=n2∈{20, 25, 30, 35, 40, 45, 50}. Assume
| $ \mathit{\boldsymbol{Y}}=\mathit{\boldsymbol{X \gamma}}\text{ }+\mathit{\boldsymbol{G \beta}}\text{ }+\epsilon , $ | (4) |
where X~N(0, Σ), Σ=(σij) with σii=1 and σij=0.2(i≠j) for i, j∈{1, 2, 3, 4}, G is a column of the group status indicator, γ is the matrix with the element being 1,
To evaluate the type Ⅰ error rate, we set βv=0, v=1, 2, …, 10. 1 000 replicates are conducted and the nominal significance level is set to be 0.05. The results for Log-normal and Laplace distributions are summarized in Table 1 and Table 2, respectively. In Table 1, it is seen that the HT is a little bit conservative with the empirical type Ⅰ error rates being less than 0.05 and the MAX is optimistic when the sample size is small. The other three tests maintain good type Ⅰ error rates, which are close to 0.05. Similar phenomena are observed in Table 2. For example, when the data are Log-normal distributed with the sample size of 40, the empirical type Ⅰ error rates of HT, RST, ARST, MAX, and MIN2 are 0.038, 0.048, 0.047, 0.069, and 0.046, respectively, as ρ=0.3 and 0.034, 0.045, 0.045, 0.065, and 0.048, respectively, as ρ=0.7. When the data are generated from the Laplace distribution with the sample size of 40, the empirical type Ⅰ error rates of HT, RST, ARST, MAX, and MIN2 are 0.054, 0.046, 0.047, 0.072, and 0.046, respectively, as ρ=0.3 and 0.054, 0.049, 0.050, 0.066, and 0.052, respectively, as ρ=0.7.
|
|
Table 1 The empircial type Ⅰ error rates of HT, RST, ARST, MAX, and MIN2 when the data are generated from ten-dimensional Log-normal distribution |
|
|
Table 2 The empircial type Ⅰ error rates of HT, RST, ARST, MAX, and MIN2 when the data are generated from ten-dimensional Laplace distribution |
To make power comparison, two types of alternatives are considered:
(a) β=(0.3, 0.3, 0.3, 0.3, 0.3, -0.3, -0.3, -0.3, -0.3, -0.3)T;
(b) β=(0.5, 0.5, 0.5, 0.5, 0.5, 0, 0, 0, 0, 0)T.
The results for Log-normal and Laplace distributions are displayed in Figs. 1 and 2, respectively, with ρ=0.3 on the left panels and ρ=0.7 on the right panels. For scenario (a), we can see that the RST and ARST have smallest powers, which are close to 0.05. It is reasonable since the differences among the outcomes are counteracted. With the increase in the sample size, the powers of HT, MAX, and MIN2 increase. The MIN2 is the most powerful among all the tests. Sometimes, the power increase for MIN2 reaches more than 30% compared with other tests. For example, for Log-normal distribution, when n1=n2=30 and ρ=0.3, the empirical powers of HT, RST, ARST, MAX, and MIN2 are 0.266, 0.038, 0.040, 0.427, and 0.775, respectively. When n1=n2=30 and ρ=0.7, the empirical powers of HT, RST, ARST, MAX, and MIN2 are 0.643, 0.055, 0.064, 0.384, and 0.980, respectively. For Laplace distribution, the power increase for MIN2 is sometimes more than 10% over other tests. For example, for scenario (b) when n1=n2=25 and ρ=0.3, the empirical powers of HT, RST, ARST, MAX, and MIN2 are 0.439, 0.144, 0.151, 0.498, and 0.72, respectively. When n1=n2=25 and ρ=0.7, the empirical powers of HT, RST, ARST, MAX, and MIN2 are 0.895, 0.182, 0.190, 0.538, and 0.997, respectively.
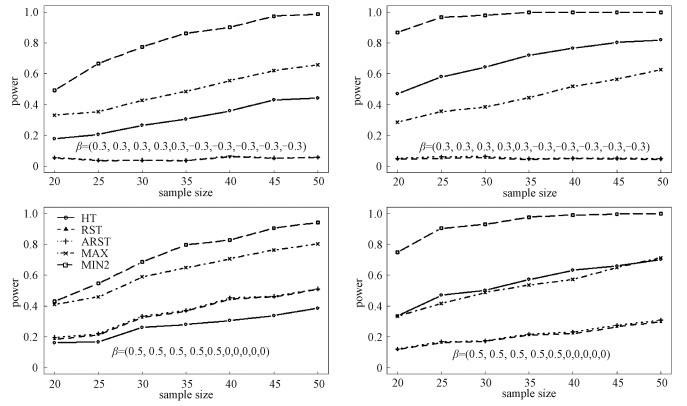
|
Download:
|
|
Left:ρ=0.3, right:ρ=0.7; the norminal significance level is 0.05 and 1 000 replicates are conducted. Fig. 1 The power values of HT, RST, ARST, MAX, and MIN2 when the data are generated from the ten-dimensional Log-normal distribution |
|
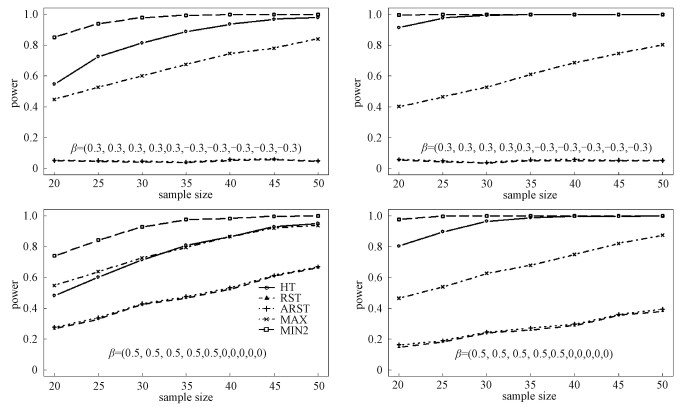
|
Download:
|
|
Left:ρ=0.3, right:ρ=0.7; the norminal significance level is 0.05 and 1 000 replicates are conducted. Fig. 2 The empirical power values of HT, RST, ARST, MAX, and MIN2 when the data are generated from the ten-dimensional Laplace distribution |
|
Next, we consider the influences of large sample size and dimension on the efficacy of our MIN2. The simulation data are generated from (4), where
(c)(β1=…=βk/2=0.05, βk/2+1=…=βk=-0.05)T;
(d)(β1=…=βk/2=0.1, βk/2+1=…=βk=0)T.
The results are shown in Table 3. It can be seen that the power of MIN2 increases with the sample size when the dimension is fixed. For example, when k=20 and ρ=0.3 under scenario(c), the empirical powers of HT, RST, ARST, MAX, and MIN2 are 0.137, 0.055, 0.054, 0.120, and 0.262 for n1=n2=100 and 0.270, 0.052, 0.052, 0.151, and 0.609 for n1=n2=200, respectively. Similarly, the power of MIN2 rises drastically with the increment of the dimension relative to other tests when the sample size is fixed. For example, when n1=n2=100 and ρ=0.7 under scenario(d), the powers of all the tests are 0.234, 0.088, 0.091, 0.148, and 0.480 for k=10, 0.344, 0.093, 0.092, 0.153, and 0.657 for k=20, and 0.434, 0.105, 0.106, 0.155, and 0.808 for k=30, respectively. So, the performance of our MIN2 is superior to the other tests in the two cases when the sample size or dimension becomes larger.
|
|
Table 3 The empircial power results of HT, RST, ARST, MAX, and MIN2 when the data are generated from the k-dimensional Laplace distribution with large sample size |
We apply the HT, RST, ARST, MAX, and MIN2 to the data on the aging human brain [3]. A total of 30 samples are divided into two groups on account of age. The ages of subjects in group 1 are less than 73 and those in group 2 are larger than 73, where the threshold of 73 is suggested by the authors of Ref.[3]. The aim is to investigate the difference between the two groups with gender as a covariate. Six gene chips (accession number), CYP11B1, CYP11B2, D26561, CEACAM7, ESRRB, and MMP15, are treated as multiple endpoints. Figure 3 shows the box-plots of six gene chips after removing the effect of gender. It is most likely that there exists difference between the two groups. Furthermore, the average values of three gene chips, CY11B1, D26561, and CEACAM7, of group 1 are less than those of group 2, but for the other gene chips, CYP11B2, ESRRB and MMP15, the results are contrary. We carry out the HT, RST, ARST, MAX, and MIN2 to detect the difference between the two groups and the p-values of the above five tests are 0.409, 0.782, 0.794, 0.243, and 0.024, respectively. Evidently, except for MIN2, the other tests fail to detect the difference between the two groups after removing effect of gender at the nominal level of 0.05.

|
Download:
|
|
Fig. 3 The box-plots of six gene chips after covariate adjustment in the aging human brain |
|
Studies involving multiple outcomes are fairly common in many research areas. Many procedures including parametric and nonparametric ones have been developed in the literature without considering covariates. Actually in applications, the auxiliary covariates may often be recorded on each subject. If some covariates are associated with outcomes, the precision may be improved by adjusting for this relationship. In this work, we propose an MIN2 test to compare the difference between two groups for multiple outcomes with covariate adjustment. Through the simulation studies, the MIN2 test controls the type Ⅰ error rate very well and has superior power to other existing nonparametric tests.
| [1] |
Brunner E, Domhof S, Langer F. Nonparametric analysis of longitudinal data in factorial Experiments[M]. New York: Wiley, 2002.
|
| [2] |
Li Z, Cao F, Zhang J, et al. Summation of absolute value test for multiple outcome comparison with moderate effect[J]. Journal of Systems Science and Complexity, 2013, 26(3): 462-469. DOI:10.1007/s11424-012-0272-5 |
| [3] |
Lu T, Pan Y, Kao S Y, et al. Gene regulation and DNA damage in the ageing human brain[J]. Nature, 2004, 429(6994): 883-891. DOI:10.1038/nature02661 |
| [4] |
Hotelling H. The generalization of Student's ratio[J]. The Annals of Mathematical Statistics, 1931, 2(3): 360-378. DOI:10.1214/aoms/1177732979 |
| [5] |
O'Brien P C. Procedures for comparing samples with multiple endpoints[J]. Biometrics, 1984, 40(4): 1079-1087. DOI:10.2307/2531158 |
| [6] |
Huang P, Tilley B C, Woolson R F, et al. Adjusting O'Brien's test to control type Ⅰ error for the generalized nonparametric Behrens-Fisher problem[J]. Biometrics, 2005, 61(2): 532-539. DOI:10.1111/biom.2005.61.issue-2 |
| [7] |
Liu A, Li Q, Liu C, et al. A rank-based test for comparison of multidimensional outcomes[J]. Journal of the American Statistical Association, 2010, 105(490): 578-587. DOI:10.1198/jasa.2010.ap09114 |
| [8] |
Grouin J M, Day S, Lewis J. Adjustment for baseline covariates:an introductory note[J]. Statistics in medicine, 2004, 23(5): 697-699. DOI:10.1002/(ISSN)1097-0258 |
| [9] |
Koch G G, Tangen C M, Jung J W, et al. Issues for covariance analysis of dichotomous and ordered categorical data from randomized clinical trials and non-parametric strategies for addressing them[J]. Statistics in medicine, 1998, 17(15/16): 1863-1892. |
| [10] |
Lesaffre E, Senn S. A note on non-parametric ANCOVA for covariate adjustment in randomized clinical trials[J]. Statistics in medicine, 2003, 22(23): 3583-3596. DOI:10.1002/(ISSN)1097-0258 |
| [11] |
Tsiatis A A, Davidian M, Zhang M, et al. Covariate adjustment for two-sample treatment comparisons in randomized clinical trials:A principled yet flexible approach[J]. Statistics in medicine, 2008, 27(23): 4658-4677. DOI:10.1002/sim.v27:23 |
| [12] |
Zhang M, Tsiatis A A, Davidian M. Improving efficiency of inferences in randomized clinical trials using auxiliary covariates[J]. Biometrics, 2008, 64(3): 707-715. DOI:10.1111/j.1541-0420.2007.00976.x |
| [13] |
McArdle B H, Anderson M J. Fitting multivariate models to community data:a comment on distance-based redundancy analysis[J]. Ecology, 2001, 82(1): 290-297. DOI:10.1890/0012-9658(2001)082[0290:FMMTCD]2.0.CO;2 |
| [14] |
Li Q, Wacholder S, Hunter D J, et al. Genetic background comparison using distance-based regression, with applications in population stratification evaluation and adjustment[J]. Genetic epidemiology, 2009, 33(5): 432-441. DOI:10.1002/gepi.v33:5 |
| [15] |
Pan W. Relationship between genomic distance-based regression and kernel machine regression for multi-marker association testing[J]. Genetic epidemiology, 2011, 35(4): 211-216. |
| [16] |
Wessel J, Schork N J. Generalized genomic distance-based regression methodology for multilocus association analysis[J]. The American Journal of Human Genetics, 2006, 79(5): 792-806. DOI:10.1086/508346 |
| [17] |
Zapala M A, Schork N J. Multivariate regression analysis of distance matrices for testing associations between gene expression patterns and related variables[J]. Proceedings of the national academy of sciences, 2006, 103(51): 19430-19435. DOI:10.1073/pnas.0609333103 |
 2019, Vol. 36
2019, Vol. 36 


