地球磁场由液态外核中的磁流体动力学(magnetohydrodynamics, MHD)过程所产生和维持,这一机制被称为地磁场发电机[1]。热浮力和组份浮力为这一过程提供能量,驱动导电流体形成对流。发电机数值模拟意在通过数值计算,得到自持式发电机过程[2]。从1950年代到1990年代,发电机理论已经证实外核发电机过程的可行性和基本条件。然而,只有当MHD数值计算足够成熟后,地磁场发电机的数值结果才可以展示所观测的地磁场详细性质[3]。
随着MHD数值模拟技术的成熟与大规模高性能计算机的飞速发展,发电机模拟在1995年迎来了突破。Glatzmaier和Roberts[4]的发电机模型GR95,不仅得到了三维自持发电机解,也展现了地磁场的一些基本形态特征和物理过程,例如偶极占优、地磁西漂和磁极倒转。此外,GR95模型还研究内外核黏性耦合以及电磁耦合给内核差动旋转带来的影响[5],并被随后的地震波研究所证实[6]。其后陆续有新的发电机模型被建立,如Kageyama等; Kuang和Bloxham; Christensen等; Fearn; Dormy等; Jones等; Busse; Zhang和Schubert; Kono和Roberts; Glatzmaier等和Takahashi等等[7-10]。大多数模型可以近似吻合地磁场的空间谱、长期变化以及地磁场倒转等现象。近年来,科学家已经能够逐渐运用发电机数值模拟结果解释地球、行星[11]和恒星[12-13]磁场的一些特殊性质与机制[14]。
然而,由于发电机模型参数还没有达到完全类地行为所需的极端分辨率,所以这些数值模型还不能解释关于地磁场发电机是如何运作的很多基本问题。特别是,期望外核的流场展现大范围的长度特征尺度,从黏性边界层的厚度(~0.1 m)到地核半径(~7×106 m),外加一个相当完整的时间范围,都是现在模型无法实现的[15]。研究人员通过采用比实际地核值大很多的黏性扩散和热扩散值来解决这个问题,例如假设超大的黏性值用以压制小尺度的湍流运动。但是对小尺度湍流的抑制是否会严重影响发电机过程的物理本质仍然是一个悬而未决的问题[3]。
本文简述地磁场发电机基准模型的方程组、无量纲方案、初始条件边界条件、数值方法和标度律等基本问题,并且以MoSST模型为例展示数值模拟结果,在文章的最后展望地磁场发电机数值模拟的未来发展。
1 地磁场发电机模型基础一个成功的自持式地磁场发电机模型需要满足一些基本的条件:1)一个合理的动力机制来驱动导电流体运动。大部分模型假设的驱动力是热动力和/或组份对流,少部分模型假设的驱动力是地球进动[16];2)Cowling反发电机理论证明,轴对称磁场不可能由轴对称运动所维持[17]。因此地磁场发电机模型中的流场和磁场必须都是三维的,球形的几何结构也是再现地球全球偶极磁场占优的根本要素;3)模型必须是旋转的。因为科氏力是构建流场结构和产生全球偶极磁场占优的关键因素[1]。
相比于以上因素,关于地核其他性质的假设就没有那么重要了。在大多数模型中,忽略密度的可压缩性和地核的径向热结构。取而代之的是使用布辛涅斯克近似,温度和组份的改变只通过Navier-Stokes方程(N-S方程)的浮力项输入,进而改变密度[18]。从这个角度看,地磁场发电机的数值模型和气体行星或恒星发电机数值模型有着较大的差异[19]。大多数的地磁场发电机模型的物质属性都是常数,外核是一个可旋转的液态球壳。在球壳内部,内核的电导率和外核一样(有些模型把内核简化为绝缘体),在球壳外部是绝缘的地幔。
根据以上这些方法可以构建一种最简单的模型,把它定义为地磁场发电机数值模型的基准模型[20]。在接下来的章节,我们都是以基准模型为参考,讨论各种发电机模型的不同修改。
1.1 地磁场发电机方程组球坐标下发电机模型的控制方程组由动量方程(Navier-Stokes方程)、磁感应方程、热对流方程以及速度场和磁场的无散约束构成。其中,N-S方程包含科氏力项和洛伦兹力项;由麦克斯韦方程组推出的磁感应方程中忽略位移电流[21-22]:
| $ \begin{array}{l} \left( {{\partial _t} + \mathit{\boldsymbol{u}} \cdot \nabla } \right)\mathit{\boldsymbol{u}} + 2\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{u}} = \\ - \nabla P + \frac{1}{{{\rho _0}}}\mathit{\boldsymbol{J}} \times \mathit{\boldsymbol{B + }}\frac{{\Delta \rho }}{{{\rho _0}}}g + \nu {\nabla ^2}\mathit{\boldsymbol{u}},\\ \left( {{\partial _t} - \eta {\nabla ^2}} \right)\mathit{\boldsymbol{B}} = \nabla \times \left( {\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{B}}} \right),\\ \left( {{\partial _t} - \kappa {\nabla ^2}} \right)T = - \mathit{\boldsymbol{u}} \cdot \nabla T + \varepsilon ,\\ \nabla \cdot \mathit{\boldsymbol{u}} = 0,\\ \nabla \cdot \mathit{\boldsymbol{B}} = 0. \end{array} $ | (1) |
式中:u为外核内流体的流动速度;Ω为地球自转角速度;P为修正后的压力(P=p-
一些模型忽略N-S方程中的惯性项[4-5],或做简化处理只保留轴对称分量[8, 23-24]。这样处理除简化的因素外,是由于对地球而言,惯性力相比于科氏力和洛伦兹力要小得多。然而没有任何一个模型直接比较有或没有惯性力项的情况,在地核条件下惯性力也许起的作用很小,这仍是一个未知问题。
大多数发电机数值模型假设流体不可压缩并采用Boussinesq近似,然而Glatzmaier和Roberts[23]及随后的一些模型考虑了密度分层结构和其他非Boussinesq近似的影响,如扩散率对热方程的贡献。在这些模型中,使用滞弹性假设,不同于通过压制声波的完全可压缩形式。Gastine等[25]对此进行系统的研究,结果表明当层间密度差超过4倍时,磁场将会变为非偶极场。如果地球外核是密度差为1.2倍的弱密度分层结构,则可能会对磁场形态和发电机系统有重要的影响[26-27]。
1.2 无量纲方案大部分模型对方程组(1)进行无量纲化处理,然而无量纲化方案有很多种,所以不同的地磁场发电机模型使用不同的无量纲参数[4-5, 8, 24, 27]。对于对流驱动型发电机模型来说,基本有4个独立的无量纲参数。在地磁场发电机基准模型的定义中,以D=ro-ri为长度特征尺度(ro为外核半径,ri为内核半径,基准模型中ri/ro=0.35),黏性扩散时间t=D2/ν为时间特征尺度,B=(ρμ0ηΩ)1/2为磁场特征尺度,以内外核边界的温度差ΔT为温度特征尺度,将方程组(1)无量纲化,得到地磁场发电机模型的无量纲化方程组:
| $ \begin{array}{l} E\left( {{\partial _t} + \mathit{\boldsymbol{u}} \cdot \nabla } \right)\mathit{\boldsymbol{u}} + 2\mathit{\boldsymbol{z}} \times \mathit{\boldsymbol{u}} = \\ - \nabla P + \frac{1}{{Pm}}\nabla \times \mathit{\boldsymbol{B}} \times \mathit{\boldsymbol{B}} + E{\nabla ^2}\mathit{\boldsymbol{u}} + {R_a}\frac{r}{{{r_o}}}T,\\ \left( {{\partial _t} - \frac{1}{{Pm}}{\nabla ^2}} \right)\mathit{\boldsymbol{B}} = \nabla \times \left( {\mathit{\boldsymbol{u}} \times \mathit{\boldsymbol{B}}} \right),\\ \left( {{\partial _t} - \frac{1}{{\mathit{Pr}}}{\nabla ^2}} \right)T = - \mathit{\boldsymbol{u}} \cdot \nabla T + \varepsilon ,\\ \nabla \cdot \mathit{\boldsymbol{u}} = 0,\\ \nabla \cdot \mathit{\boldsymbol{B}} = 0. \end{array} $ | (2) |
式中:单位向量z为旋转轴的方向,假设重力与半径为线性的关系g(r)=gor/ro,go为外核边界(CMB)的重力值。式中的无量纲参数定义如表 1所示。
|
|
表 1 地磁场发电机数值基准模型各无量纲参数定义 Table 1 Definitions of dimensionless parameters in geodynamo benchmark |
表 1中的外核估值根据参数定义计算得到,所用到的扩散系数等物理参数的估值可参考Olsen等[28]、Christensen和Wicht[3]的研究结果。从表 1可以看出,这些参数在数值模拟中的取值与实际值仍存在较大差距,目前的计算能力还远远无法达到参数的估计数量级。
无量纲方程组和无量纲参数的不同是由于所选取的特征尺度不同造成的。对于长度特征尺度,部分模型选择ro代替D。对于时间特征尺度,部分模型选择磁扩散时间或者热扩散时间来代替黏性扩散时间。同样对于磁场特征尺度和温度场特征尺度的定义也有差异[3]。由此就会导致不同的模型定义不同的无量纲参数,从而造成数值计算的复杂及多样性,但是通常来说其他无量纲参数都可以由基准模型中的4个无量纲参数表示[10]。
地磁场发电机模型的数值解也需要用无量纲诊断参数来表示。比较常见的几个无量纲诊断参数为磁Reynolds数Rm,Reynolds数Re,Rossby数Ro,Elsasser数Λ,其定义如表 2所示。
|
|
表 2 地磁场发电机数值基准模型各无量纲诊断参数定义 Table 2 Definitions of dimensionless diagnostic parameters in geodynamo benchmark |
除用无量纲诊断参数表示数值解以外,还可以用诊断图来判断数值模拟的结果是否达到稳定状态,具体的诊断图将会在下章讨论。
1.3 初始条件地磁场发电机数值模型的初始条件由Christensen等所定义[20],速度场初始条件为
| $ u = 0. $ | (3) |
温度场初始条件为
| $ \begin{array}{*{20}{c}} {T = \frac{{{r_{\rm{o}}}{r_{\rm{i}}}}}{r} - {r_{\rm{i}}} + \frac{{21}}{{\sqrt {17\;920{\rm{ \mathsf{ π} }}} }}\left( {1 - 3{x^2} + } \right.}\\ {\left. {3{x^4} - {x^6}} \right){{\sin }^4}\theta {{\cos }^4}\phi .}\\ {其中\;x = 2r - {r_{\rm{i}}} - {r_{\rm{o}}};} \end{array} $ | (4) |
磁场初始条件为:
| $ {B_r} = \frac{5}{8}\left( {8{r_{\rm{o}}} - 6r - 2\frac{{r_{\rm{i}}^4}}{{{r^3}}}} \right)\cos \theta , $ | (5) |
| $ {B_\theta } = - \frac{5}{8}\left( {8{r_{\rm{o}}} - 9r + \frac{{r_{\rm{i}}^4}}{{{r^3}}}} \right)\sin \theta , $ | (6) |
| $ {B_\phi } = 5\sin \left( {{\rm{ \mathsf{ π} }}\left( {r - {r_{\rm{i}}}} \right)} \right)\sin 2\theta . $ | (7) |
边界条件对于地磁场发电机数值模型非常重要,控制着地幔和内核的差异转动。这种差异转动是由净扭矩产生的,扭矩主要包括黏性扭矩和电磁扭矩。由于所关注的问题有差异,地磁场发电机数值模型的边界条件分为很多种类。同时,不同的边界条件也会造成定义不同的无量纲参数。这一节系统讨论不同的边界条件对于发电机数值模拟的影响。
1.4.1 速度边界条件对于速度场来说,最简单的发电机模型假设外核为一个刚性的、不可穿透且共旋的球壳。这意味着在旋转坐标下,速度场所有分量在边界处均为0,即no-slip边界条件:
| $ \left[ \mathit{\boldsymbol{u}} \right] = 0. $ | (8) |
[ ]表示通过边界的区别。Kuang和Bloxham[8]认为如果使用no-slip边界条件,模型中所使用的过大的Ekman数会导致过大的Ekman-layer影响,所以他们使用free-slip速度边界条件从而消除Ekman-layer的影响:
| $ {\mathit{\boldsymbol{1}}_n}\mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{1}}_n} \times \left( {{\mathit{\boldsymbol{\sigma }}_\nu } \cdot {\mathit{\boldsymbol{1}}_n}} \right) = 0. $ | (9) |
式中:1n为边界法向量,σν为黏性应力张量。
现有数值模型不能解释为什么内核会和地幔共旋。部分模型的坐标系下内核和地幔的旋转是有差异的[4-5, 8]。而转速的差异是由净扭矩产生的,当忽略重力扭矩时,Glatzmaier和Roberts[29]发现通过内核边界的耦合,内核每年多旋转几度。随后地震学证实存在这样的差异旋转,并证明差异旋转速率很小[30-31]。当考虑内核和地幔的重力耦合后的发电机模型,也得出了较小的内核旋转速率[32]。
1.4.2 磁场边界条件对于磁场来说,当假设地幔和内核均为绝缘体时,液核磁场在内部和外部均为一个连续势场。基于球谐函数的谱方法很容易满足这个条件[33],而局域法则不能满足。在一些数值模型中,运用水平磁场分量为0的边界条件[7, 34-36]。在边界处只有非零径向场分量,即称为“准真空条件”,是不合实际的。然而其得到的数值解,与更真实的绝缘外部区域条件所得的数值解性质相似[34]。所以如果不关注外部场结构的研究,则可使用准真空条件简化数值方法[3]。
假设内核为绝缘体显然也是不合实际的,在通常的数值模型中,假设内核与外核有相同的电导率。这种情况下,必须在内核内解磁感应方程,其速度场只是单纯地描述固态内核坐标系下的固体旋转速率。在内核边界,应用磁场和电场水平分量的连续条件。Hollerbach和Jones[37]提出的一个简化的平均场发电机模型结果表明,内核使用有限电导边界条件,对于使得发电机产生一个稳定的偶极场起重要作用:
| $ \left[ \mathit{\boldsymbol{B}} \right] = \left[ {{{\bf{1}}_n} \times \mathit{\boldsymbol{J}}} \right] = \left[ {{{\bf{1}}_n} \times \mathit{\boldsymbol{E}}} \right] = 0. $ | (10) |
E为无量纲电场。在一系列的MHD模型中,包括一些偶极倒转的模型,Wicht[38]发现当其他条件一致时,内核绝缘和可导结果相差无几。作为对比,Dharmaraj和Stanley[39]指出,内核电导率可以强化模型的偶极占优并且减少倒转次数。他们认为Wicht的研究结果的差异主要是其使用固定热流边界条件代替了固定温度边界条件。
另外一些模型[5, 24]没有假设地幔是可导的,而是用一个电导率适中的薄层作为地幔的底部。Kuang和Bloxham[24]的模型在CMB外面包含一个电导率为其1/10的D”层。其主要目的是使地幔和外核通过地磁扭矩达到核幔耦合。目前,电导层对于发电机过程的影响并没有系统的研究,但是被认为影响很小[3]。
1.4.3 热边界条件对于地球外核来说,驱动其对流的是热浮力和组份浮力两部分,前者的来源是内核固化和地核长期冷却所释放的潜热,后者则是由于轻元素的释放从而加固了内核[40-41]。实验证明地核内可能存在放射性元素钾,但是仍有争议[42-43]。而对流的地幔控制着地核的热损耗,其有效地给地磁场发电机在CMB强加了一个固定热流的边界条件
| $ \frac{{\partial \theta }}{{\partial r}} = 0. $ | (11) |
热流是随时空变化的,地幔对流的时间尺度是几十到上百万年,相对于发电机的时间尺度要更长一些。因此在地磁场发电机模型中,除Driscoll和Olson的模型[44]外,其余的模型均忽略时间变化,而在一些模型中,考虑了空间变化[3]。
许多模型在内核和外核边界之间强加一个固定温度边界条件
| $ \theta = 0. $ | (12) |
这个简化条件没有物理根据,但是却证明热边界条件似乎对发电机过程没有影响。然而Sakuraba和Roberts[45]、Hori等[46-47]认为,热边界条件对于流场尺度和磁场形态有很大影响。内核边界条件的物理形式不如外核边界条件那么清晰。内核任何一个可能的平移运动也许会导致铁的半球熔化,从而形成稳固的分层结构[48]。这类复杂的研究工作目前还没有开展。
1.5 数值方法目前发电机模型的数值方法有两类:谱方法和局域法。大多数发电机模型采用的是谱方法。Bullard和Gellman[49]首次应用谱方法解发电机方程组的微分方程。最初使用的Galerkin方法[49-51]已经被更有效的谱方法所替代。对于地磁场发电机来说,首先由Glatzmaier和Roberts[5]提出(其最早应用于恒星发电机模型),随后被其他模型使用。在谱方法中,未知数在径向上采用Chebyshev展开,球面上用球谐函数进行展开。这使得谱方法求导简单,并且有较好的收敛性,但是其在并行计算中需要消耗大量的节点进行计算和通信。一些发电机模型采用超扩散从而保证计算的稳定性[4-5, 8, 23-24, 52-53]。本文将在下一个章节具体介绍超扩散的引用。
近些年一些发电机数值模型发展使用了局域法:有限差分法、有限元法、有限体积法和谱元法。选择局域法有以下几个原因:1)可以对球壳进行更灵活的分解;2)一些局域法更容易实现,而且所有局域法的并行化都比谱方法的并行化简单;3)局域法避免了在每个时间步的Legendre转换,从而节省大量的计算资源[54]。比较不同架构上不同代码的性能是一项艰巨的任务,特别是考虑绝对运行时间或计算性能时。尽管局域法在大型并行计算上的运行效率比谱方法要高,但谱方法的计算速度仍然保持在数千个处理器以上[55]。
1.6 无量纲参数的标度律地磁场发电机的数值模拟还有很多问题亟待解决,其中一个重要的障碍就是模型参数与真实参数的差异问题[56]。受限于计算能力,发电机模型难以求解快速旋转以及低黏性参数(相对应较小的Ekman数),目前所取参数(E~10-5)与估计参数(E~10-15)甚至达到近10个量级的差异[57]。这一鸿沟依靠计算技术的发展短期内仍难以解决。Davies等[58]估计即便模型所用黏性与估计黏性仅相差6个量级(E ~10-9),也需要54 000个可用的进程运行至少13 000天以得到一个磁扩散时间的数值,这对于数值计算来说是个巨大的挑战。
鉴于数值计算的参数取值与实际值的巨大差距,标度律的研究对于发电机研究十分重要。一方面,完善的标度律是理解发电机理论的重要组成部分。另一方面,其可以预测地球不同时期的古磁场强度,或者将地球发电机的特性与其他行星上的发电机相关联[59]。从Christensen、Aubert和Tilgner开始,研究人员利用发电机数值模拟来推导(或测试)标度律[56, 60-61]。其中有关于某一个参数的标度律,如Ra[28, 62-64],E[65]和Pm[66-67];也有一些是系统性研究各个无量纲参数的标度律[9, 14, 56]。研究得到许多比例关系及定量结论,例如发电机磁场在什么参数区间表现为偶极场占优,何时由多极场主导[4];如何由给定参数估算流场和磁场的强弱[68],以及磁场强弱是否与各种扩散系数相关[56]等等,具体可参考Christensen[59]的研究。
2 MoSST模型介绍MoSST模型由Kuang和Bloxham[8]提出,其定义的无量纲参数为:表征热驱动大小的Rayleigh数Ra,表征黏滞效应与旋转效应之比的Ekman数E,表征惯性项和科里奥利力项之比的磁Rossby数Ro,和表征热扩散与磁扩散之比的磁Prandtl数qκ。MoSST模型在半径方向采用4阶紧致有限差分法求解,使用Chebyschev多项式展开作为径向网格配置节点。对于内核、外核和D”层,选取的节点数分别为35,39和19。在球面上,采用球谐展开和拟谱法求解,用FFT进行快速谱变换。球谐展开的截断阶数分别为:lmax=33, mmax=21。根据截断阶数,设置球向网格节点数分别为:θ向50个,ϕ向64个。模拟中所求解的网格数一共为277 830个。
为避免高阶球谐截断对系统的影响,以及减少从初始状态到最终状态之间的过渡时间,MoSST模型中引入超扩散[24],定义如下:
| $ \nu = \left\{ {\begin{array}{*{20}{c}} {{\nu _0},}&{{\rm{for}}\;l \ll {l_0}}\\ {{\nu _0}\left[ {1 + {{\left( {l - {l_0}} \right)}^2}} \right],}&{{\rm{for}}\;l > {l_0}} \end{array}} \right.. $ | (13) |
式中l为球谐阶数。同样的,引入热超扩散和磁超扩散。该处理方法由Glatzmaier和Roberts[5]得到首个三维自洽发电机数值模型(GR95)时引入。但以上形式相对于GR95,已经是一种弱形式。本文模拟中设定l0=4, ε=0.05。
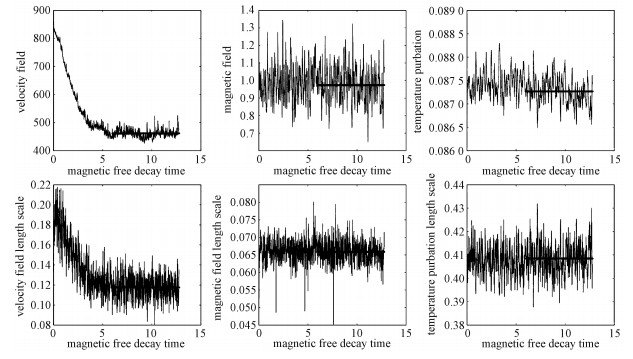
2.1 诊断输出由于发电机方程组是一个各物理场高度耦合的非线性系统,当初始状态输入以后,在各无量纲参数的约束下,系统需要一段时间进行演化迭代以达到与所选参数相对应的最终状态。判断系统是否已经演化到终态,依赖诊断输出而实现。图 1给出一个诊断输出图的例子,横坐标为演化时间,以磁自由扩散时间τf=r02/π2η为度量尺度(取r0=3.5×106 m, η=2 m2/s, τf≈2×104 a);图 1的纵坐标分别表示速度场(VF)、磁场(MF)和温度场扰动(TP)、以及3个物理场所对应的典型空间尺度:速度场典型尺度(VFLS)、磁场典型尺度(MFLS)、温度扰动典型尺度(TPLS)。
|
Download:
|
| 图 1 诊断输出示例 Fig. 1 Diagnostic outputs example | |
诊断输出中的物理量为整个外核内的均方根结果,以外核流速为例:
| $ {u_{{\rm{rms}}}} = {\left\| {{u_{{\rm{outercore}}}}} \right\|_2} = \sqrt {u_1^2 + u_2^2 \cdots + u_N^2} . $ | (14) |
其典型尺度也是均方根结果,由以下公式计算得到:
| $ {\rm{VFLS}} = {\left\| {\frac{u}{\omega }} \right\|_2} = {\left\| {\frac{u}{{\nabla \times u}}} \right\|_2}. $ | (15) |
结合图 1,判断稳定输出的根据是:所有物理量及其典型空间尺度都已稳定达到一个τf以上。最终取的输出结果为一个稳定的τf以上时间范围内(不包含开始的过渡阶段)的平均结果,由图中直线所示。本文所采用的MoSST模型是串行计算,计算时间依参数选择、初始状态、超扩散大小以及硬件性能而定。一般而言,得到图 1所示的稳定输出结果需要4~5天时间,但在极端情形下,得到一组稳定输出需要两周甚至更长时间[69]。
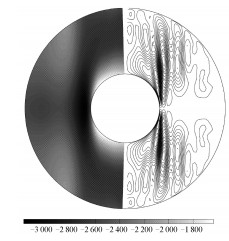
2.2 流场和磁场形态图 2为地磁场发电机流场形态图,图中给出的是子午面剖视图,其包含左右两个部分,其中左半边代表轴对称(m=0)环型流场,右半边的线条代表轴对称极型流场。每幅图都是一段时间内的输出平均后的结果。环型流场(uT)和极型流场(uP)由下式定义:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_{\rm{T}}} + {\mathit{\boldsymbol{u}}_{\rm{P}}} = \nabla \times {T_u}{\mathit{\boldsymbol{1}}_r} + \nabla \times \nabla \times {P_u}{\mathit{\boldsymbol{1}}_r}. $ | (16) |
|
Download:
|
| 图 2 轴对称流场形态图 Fig. 2 Axisymmetric velocity field | |
剖视图的左半边是速度的ϕ向分量uφ,右半边是流线图(Ψu),定义如下:
| $ {\mathit{\boldsymbol{u}}_S} = {\mathit{\boldsymbol{u}}_\varphi }\left( {r,\theta } \right) + \nabla \times \frac{{{\mathit{\Psi }_u}}}{s}{\mathit{\boldsymbol{1}}_\varphi }. $ | (17) |
式中s=r·sinθ,为场点到地球自转轴的距离。
由图 2可知,不论是极型场还是环型场,地磁场发电机的流动主要集中在正切圆柱(轴向与自转轴重合,与内核在ICB赤道面内切,与CMB在近极区外接的柱体)内,并且流动尺度大小不一。从左侧环型场来看,流动除了活跃在正切圆柱内,在圆柱体的上下两个底面流动也很显著。由于MoSST模型中超扩散的使用,压制了小尺度的对流,使得数值结果为尺度较大的运动,真实地核内的流动是非常复杂的。
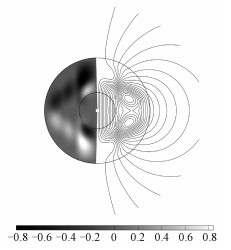
同样图 3给出轴对称磁场的分布图。从左侧环型场可以看出,磁场主要集中在正切圆柱内,并且以赤道为对称轴,上下半球的磁场极性是相反的。从极型磁场可以看出,虽然外核内存在多个磁极子,但是CMB以外的磁场(只有极型场存在)是偶极占优[69]。
|
Download:
|
| 图 3 轴对称磁场形态图 Fig. 3 Axisymmetric magnetic field | |
虽然在可预见的未来,地磁场发电机数值模型的参数达到类地值是不可能的,但是发电机数值模型依然是研究地磁场的主要手段。经过20多年的研究,地磁场发电机模型取得了重大的进展,成功模拟出强度相当且偶极占优的磁场,重现了地磁场倒转、西漂等地磁场行为。
然而我们也要看到局限的一面,基本控制参数的值不能与地球实际值相匹配。最早的地磁场发电机模型中,参数值被随意选择或根据数值计算的可行性进行选择。近年来,标度律的建立取得了重大进展,这表明尽管存在较大的参数差异,但数值模型可能会与实际的地磁场发电机处于相同的动力机制。到目前为止,这些标度律是经验主义,其有效性的范围还不清楚。为了更好地巩固它们,运用实际参数进行模拟,则需要发展数值计算,并且运用大量的计算资源。下一代的地磁场发电机模拟系统将在千万亿次计算机上执行更真实的参数。为了实现千万亿次计算机的能力,2D或者3DMPI并行化或MPI-OpenMP混合并行化是需要的[14]。
地磁场发电机的数值模拟仍有很多问题悬而未决:Boussinesq近似合理还是非Boussinesq近似合理,并且会产生怎样的影响?核幔边界和内核边界最合适的边界条件和耦合条件是什么,以及这对发电机有何影响?组份浮力和热浮力(双扩散对流)的相互作用如何影响发电机?在地核的顶部是否有稳定的分层以及这将如何影响发电机?黏性摩擦在发电机模型中有多重要,而Ekman数的影响是否可以忽略不计?模型计算方面的问题:在径向方向上分辨率不断增大的解的收敛速度是未知的;包含湍流运动的模型的程序精度是否需要新的基准测试?修正了的时间步是否精确有效?
地球并不是太阳系中唯一有磁场的行星。研究其他行星的磁场发电机将会极大地促进地磁场发电机模型的发展。目前,涵盖行星磁场的多样性的比较发电机理论还处于起步阶段[11]。同时,地磁数据同化有助于改进未来几十年磁场演化的预测。实际的地磁观察可以在数据同化的环境中来构建模型,更好地表示地球深部的动力状态。随着计算能力的不断提升,不久的将来,地磁场发电机的数值模拟还会取得更大的进展,从而为理解地磁场提供有力的帮助。
感谢焦立果副研究员提供的MoSST模型程序及悉心指导。感谢天河一号提供计算资源。| [1] |
Roberts P H. Theory of the Geodynamo[M]. Oxford: Elsevier, 2015: 57-90.
|
| [2] |
Buffett B A. Earth's Core and the Geodynamo[J]. Science, 2000, 288(5473): 2007-2012. DOI:10.1126/science.288.5473.2007 |
| [3] |
Christensen U R, Wicht J. Numerical dynamo simulations[M]. Oxford: Elsevier, 2015: 245-277.
|
| [4] |
Glatzmaier G A, Roberts P H. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal[J]. Nature, 1995, 377(6546): 203-209. DOI:10.1038/377203a0 |
| [5] |
Glatzmaier G A, Roberts P H. A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle[J]. Physics of the Earth and Planetary Interiors, 1995, 91(1-3): 63-75. DOI:10.1016/0031-9201(95)03049-3 |
| [6] |
Song X R, Paul G. Seismological evidence for differential rotation of the Earth's inner core[J]. Nature, 1996, 382(6588): 221-224. DOI:10.1038/382221a0 |
| [7] |
Kageyama A, Sato T. Computer simulation of a magnetohydrodynamic dynamo. Ⅱ[J]. Physics of Plasmas, 1995, 2(5): 1421-1431. DOI:10.1063/1.871485 |
| [8] |
Kuang W, Bloxham J. An Earth-like numerical dynamo model[J]. Nature, 1997, 389(6649): 371-374. DOI:10.1038/38712 |
| [9] |
Christensen U R, Olsen P, Glatzmaier G A. Numerical modelling of the geodynamo a systematic parameter study[J]. Geophys J Int, 1999, 138(2): 393-409. DOI:10.1046/j.1365-246X.1999.00886.x |
| [10] |
Kono M, Roberts P H. Recent geodynamo simulations and observations of the geomagnetic field[J]. Reviews of Geophysics, 2002, 40(4): 1-53. |
| [11] |
Stanley S, Glatzmaier G. Dynamo models for planets other than Earth[J]. Space Science Reviews, 2010, 152: 617-650. DOI:10.1007/s11214-009-9573-y |
| [12] |
Glatzmaier G A. Numerical simulation of stellar convective dynamos. 1. The model and methods[J]. Journal of Computational Physics, 1984, 55(3): 461-484. DOI:10.1016/0021-9991(84)90033-0 |
| [13] |
Omara B, Miesch M S, Featherstone N A, et al. Velocity amplitudes in global convection simulations:the role of the Prandtl number and near-surface driving[J]. Advances in Space Research, 2016, 58(8): 1475-1489. DOI:10.1016/j.asr.2016.03.038 |
| [14] |
Jones C A. Planetary magnetic fields and fluid dynamos[J]. Annu Rev Fluid Mech, 2011, 43: 583-614. DOI:10.1146/annurev-fluid-122109-160727 |
| [15] |
Matsui H, Heien E M, Aubert J, et al. Performance benchmarks for a next generation numerical dynamo model[J]. Geochemistry Geophysics Geosystems, 2016, 17(5): 1586-1607. DOI:10.1002/2015GC006159 |
| [16] |
Tilgner A. Precession-driven dynamos[J]. Physics of Fluids, 2005, 17(3): 34-104. |
| [17] |
Cowling T G. The stability of gaseous stars[J]. Monthly Notices of the Royal Astronomical Society, 1934, 94(8): 768-782. DOI:10.1093/mnras/94.8.768 |
| [18] |
Anufriev A P, Jones C A, Soward A M. The Boussinesq and anelastic liquid approximations for convection in the Earth's core[J]. Physics of the Earth and Planetary Interiors, 2005, 152(3): 163-190. DOI:10.1016/j.pepi.2005.06.004 |
| [19] |
Jones C A. Thermal and Compositional Convection in the Outer Core[M]. Oxford: Elsevier, 2015: 115-159.
|
| [20] |
Christensen U R, Aubert J, Cardin P, et al. A numerical dynamo benchmark[J]. Physics of the Earth and Planetary Interiors, 2001, 128: 25-34. DOI:10.1016/S0031-9201(01)00275-8 |
| [21] |
Gubbins D, Roberts P. Magnetohydrodynamics of the Earth's core[M]. Geomagnetism, London: Academic Press, 1987: 1-183.
|
| [22] |
Braginsky S I, Roberts P H. Equations governing convection in Earth's core and the geodynamo[J]. Geophysical and Astrophysical Fluid Dynamics, 1995, 79: 1-97. DOI:10.1080/03091929508228992 |
| [23] |
Glatzmaier G A, Roberts P H. An anelastic evolutionary geodynamo simulation driven by compositional and thermal convection[J]. Physica D, 1996, 97: 81-94. DOI:10.1016/0167-2789(96)00100-5 |
| [24] |
Kuang W, Bloxham J. Numerical modeling of magnetohydrodynamic convection in a rapidly rotating spherical shell:weak and strong field dynamo action[J]. Journal of Computational Physics, 1999, 153(1): 51-81. DOI:10.1006/jcph.1999.6274 |
| [25] |
Gastine T, Duarte L, Wicht J. Dipolar versus multipolar dynamos:the influence of the background density stratification[J]. Astronomy and Astrophysics, 2012, 546: A19. DOI:10.1051/0004-6361/201219799 |
| [26] |
Evonuk M, Samuel H. Simulating rotating fluid bodies:When is vorticity generation via density stratification important?[J]. Earth Planet. Science Letters, 2012, 317/318: 1-7. DOI:10.1016/j.epsl.2011.11.036 |
| [27] |
Glatzmaier G A, Roberts P H. Simulating the geodynamo[J]. Contemporary Physics, 1997, 38(4): 269-288. DOI:10.1080/001075197182351 |
| [28] |
Olson P, Christensen U, Glatzmaier G A. Numerical modeling of the geodynamo:mechanisms of field generation and equilibration[J]. Journal of Geophysical Research:Solid Earth, 1999, 104(B5): 10383-10404. DOI:10.1029/1999JB900013 |
| [29] |
Glatzmaier G A, Roberts P H. Rotation and magnetism of Earth's inner core[J]. Science, 1996, 274(5294): 1887-1891. DOI:10.1126/science.274.5294.1887 |
| [30] |
Makinen A M, Deuss A. Global seismic body wave observations of temporal variations in the Earth's inner core, and implications for its differential rotation[J]. Geophysical Journal International, 2011, 187(1): 355-370. DOI:10.1111/gji.2011.187.issue-1 |
| [31] |
Zhang J, Song X, Li Y, et al. Inner core differential motion confirmed by earthquake waveform doublets[J]. Science, 2005, 309(5739): 1357-1360. DOI:10.1126/science.1113193 |
| [32] |
Buffett B A, Glatzmaier G A. Gravitational braking of inner-core rotation in geodynamo simulations[J]. Geophysical Research Letters, 2001, 27(19): 3125-3128. |
| [33] |
Hollerbach R. A spectral solution of the magneto-convection equations in spherical geometry[J]. International Journal for Numerical Methods in Fluids, 2000, 32(7): 773-797. DOI:10.1002/(ISSN)1097-0363 |
| [34] |
Harder H, Hansen U. A finite-volume solution method for thermal convection and dynamo problems in spherical shells[J]. Geophysical Journal International, 2005, 161(2): 522-532. DOI:10.1111/gji.2005.161.issue-2 |
| [35] |
Kageyama A, Sato T. Dipole field generation by an MHD dynamo[J]. Plasma Physics and Controlled Fusion, 1997, 39: 83-92. DOI:10.1088/0741-3335/39/1/006 |
| [36] |
Li J, Sato T, Kageyama A. Repeated and sudden reversals of the dipole field generated by spherical dynamo action[J]. Science, 2002, 295(5561): 1887-1890. DOI:10.1126/science.1066959 |
| [37] |
Hollerbach R, Jones C A. A geodynamo model incorporating a finitely conducting inner core[J]. Physics of the Earth and Planetary Interiors, 1993, 75(4): 317-327. DOI:10.1016/0031-9201(93)90007-V |
| [38] |
Wicht J. Inner-core conductivity in numerical dynamo simulations[J]. Physics of the Earth and Planetary Interiors, 2002, 132(4): 281-302. DOI:10.1016/S0031-9201(02)00078-X |
| [39] |
Dharmaraj G, Stanley S. Effect of inner core conductivity on planetary dynamo models[J]. Physics of the Earth and Planetary Interiors, 2012, 212/213: 1-9. DOI:10.1016/j.pepi.2012.09.003 |
| [40] |
Loper D E. Some thermal consequences of the gravitationally powered dynamo[J]. Journal of Geophysical Research, 1978, 83: 5961-5970. DOI:10.1029/JB083iB12p05961 |
| [41] |
Nimmo F. Energetics of the Core[M]. Oxford: Elsevier, 2015: 27-55.
|
| [42] |
Corgne A, Keshav S, Fei Y W, et al. How much potassium is in the Earth's core? New insights from partitioning experiments[J]. Earth and Planetary Science Letters, 2007, 256: 567-576. DOI:10.1016/j.epsl.2007.02.012 |
| [43] |
Rama Murthy V, van Westrenen W, Fei Y. Experimental evidence that potassium is a substantial radioactive heat source in planetary cores[J]. Nature, 2003, 423(6936): 163-165. DOI:10.1038/nature01560 |
| [44] |
Driscoll P, Olson P. Polarity reversals in geodynamo models with core evolution[J]. Earth and Planetary Science Letters, 2009, 282: 24-32. DOI:10.1016/j.epsl.2009.02.017 |
| [45] |
Sakuraba A, Roberts P H. Generation of a strong magnetic field using uniform heat flux at the surface of the core[J]. Nature Geoscience, 2009, 2(11): 802-805. DOI:10.1038/ngeo643 |
| [46] |
Hori K, Wicht J, Christensen U R. The effect of thermal boundary conditions on dynamos driven by internal heating[J]. Physics of the Earth and Planetary Interiors, 2010, 182: 85-97. DOI:10.1016/j.pepi.2010.06.011 |
| [47] |
Hori K, Wicht J, Christensen U R. The influence of thermo-compositional boundary conditions on convection and dynamos in a rotating spherical shell[J]. Physics of the Earth and Planetary Interiors, 2012, 196/197: 32-48. DOI:10.1016/j.pepi.2012.02.002 |
| [48] |
Alboussière T, Deguen R, Melzani M. Melting-induced stratification above the Earth's inner core due to the convective translation[J]. Nature, 2010, 466: 744-747. DOI:10.1038/nature09257 |
| [49] |
Bullard E C, Gellman H. Homogeneous dynamos and terrestrial magnetism[J]. Proceedings of the Royal Society of London A, 1954, 247(928): 213-278. |
| [50] |
Zhang K, Busse F H. Convection driven magnetohydrodynamic dynamos in rotating spherical shells[J]. Geophysical and Astrophysical Fluid Dynamics, 1989, 49: 97-116. DOI:10.1080/03091928908243466 |
| [51] |
Zhang K, Busse F H. Generation of magnetic fields by convection in a rotating spherical fluid shell of infinite Prandtl number[J]. Physics of the Earth and Planetary Interiors, 1990, 59(3): 208-222. DOI:10.1016/0031-9201(90)90226-N |
| [52] |
Sakuraba A, Kono M. Effect of the inner core on the numerical simulation of the magnetohydrodynamic dynamo[J]. Physics of the Earth and Planetary Interiors, 1999, 111: 105-121. DOI:10.1016/S0031-9201(98)00150-2 |
| [53] |
Stanley S, Bloxham J. Convective-region geometry as the cause of Uranus' and Neptune's unusual magnetic fields[J]. Nature, 2004, 428(6979): 151-153. DOI:10.1038/nature02376 |
| [54] |
Kageyama A, Yoshida M. Geodynamo and mantle convection simulations on the Earth Simulator using the Yin-Yang grid[J]. Journal of Physics:Conference Series, 2005, 16(1): 325-338. |
| [55] |
Wicht J, Stellmach S, Harder H. Numerical models of the geodynamo:from fundamental Cartesian models to 3D simulations of field reversals[M]. Berlin: Springer, 2009: 107-158.
|
| [56] |
Christensen U R, Aubert J. Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields[J]. Geophysical Journal International, 2006, 166(1): 97-114. DOI:10.1111/gji.2006.166.issue-1 |
| [57] |
Christensen U R. A sheet-metal geodynamo[J]. Nature, 2008, 454(7208): 1058-1059. DOI:10.1038/4541058a |
| [58] |
Davies C J, Gubbins D, Jimack P K, et al. Scalability of pseudospectral methods for geodynamo simulations[J]. Concurrency and Computation:Practice and Experience, 2011, 23(1): 38-56. DOI:10.1002/cpe.v23.1 |
| [59] |
Christensen U R. Dynamo scaling laws and applications to the planets[J]. Space Science Reviews, 2010, 152(1-4): 565-590. DOI:10.1007/s11214-009-9553-2 |
| [60] |
Christensen U R, Tilgner A. Power requirement of the geodynamo from ohmic losses in numerical and laboratory dynamos[J]. Nature, 2004, 429(6988): 169-171. DOI:10.1038/nature02508 |
| [61] |
Aubert J. Steady zonal flows in spherical shell dynamos[J]. Journal of Fluid Mechanics, 2005, 542(1): 53-67. |
| [62] |
Kuang W, Jiang W, Wang T. Sudden termination of Martian dynamo?:Implications from subcritical dynamo simulations[J]. Geophysical Research Letters, 2008, 35(14): L14204. DOI:10.1029/2008GL034183 |
| [63] |
王天媛, Wei Z G, Jiang W Y, 等. 数值模拟火星古发电机湮灭前磁场特征[J]. 中国科学:地球科学, 2013, 43(1): 155-162. |
| [64] |
Sreenivasan B, Sahoo S, Dhama G. The role of buoyancy in polarity reversals of the geodynamo[J]. Geophysical Journal International, 2014, 199(3): 1698-1708. DOI:10.1093/gji/ggu340 |
| [65] |
Sarson G R, Jones C A, Longbottom A W. Convection driven geodynamo models of varying Ekman number[J]. Geophysical & Astrophysical Fluid Dynamics, 1998, 88(1-4): 225-259. |
| [66] |
Simitev R, Busse F H. Prandtl-number dependence of convection-driven dynamos in rotating spherical fluid shells[J]. Journal of Fluid Mechanics, 2005, 532: 365-388. DOI:10.1017/S0022112005004398 |
| [67] |
Calkins M A, Aurnou J M, Eldredge J D, et al. The influence of fluid properties on the morphology of core turbulence and the geomagnetic field[J]. Earth Planet Sci Lett, 2012, 359/360: 55-60. DOI:10.1016/j.epsl.2012.10.009 |
| [68] |
Starchenko S V, Jones C A. Typical velocities and magnetic field strengths in planetary interiors[J]. Icarus, 2002, 157(2): 426-435. DOI:10.1006/icar.2002.6842 |
| [69] |
董超, 焦立果, 张怀, 等. 外核黏性对地磁场发电机数值模型的影响[J]. 地球物理学报, 2018, 61(4): 1366-1377. |
 2019, Vol. 36
2019, Vol. 36 


