针对互联网和物联网不断增长的移动业务需求，第五代(fifth-generation，5G)移动通信系统提出支持高达数十Gbps的峰值速率和1百万个/km²的海量连接密度的性能指标^[1]。面对5G场景中高流量密度和高连接数的技术挑战，传统以基站侧为中心的蜂窝网络将产生严重的频谱效率低和基站超负荷等问题。因此，5G通信系统考虑将基于用户侧的终端直通(device-to-device，D2D)通信作为对基站侧通信的补充机制，通过复用小区蜂窝用户频谱资源进行终端设备间的直接数据通信，减轻基站侧负载，以满足海量用户终端的连接需求、增强小区覆盖和提升整体用户速率。

D2D通信包括点对点和多播^[2]两种传输模式，其中点对点传输模式无法解决无线网络中大量重复的流行文件传输造成的资源浪费问题，因此频谱利用率较低。针对大量接收相同数据的用户密集分布在一个较小的区域内的场景，例如，在一个露天演唱会现场，所有用户需从基站下载相同的视频资源；或在一个会议现场，所有与会者需要获取相同的文件。在这类场景下，由于接收数据的用户之间距离较近，借助D2D多播来辅助基站下行传输，可以提高频谱效率和缩短端到端时延。在蜂窝网络中支持D2D多播通信模式将逐渐成为5G通信系统的主流网络架构之一^[3]。

在支持D2D多播的蜂窝网络中，D2D多播簇由簇头和簇内接收用户组成。基站先将数据发送给簇头用户，簇头与周围的接收用户组成D2D多播簇，并通过多播方式与簇内用户通信。为提高频谱利用率，D2D多播采用同频复用技术实现多播簇与蜂窝用户的频率复用，但由此产生的同频干扰将严重影响系统性能。如何进行多播簇与蜂窝用户的信道分配和功率控制以减小同频复用干扰，成为支持D2D多播的蜂窝网络中需要解决的关键问题。文献[4]研究D2D多播簇复用蜂窝上行信道时的资源分配问题，在保证蜂窝和D2D用户的服务质量(quality of service, Qos)前提下，进行功率控制和信道复用的联合优化，以降低同频复用干扰，提升系统总容量。文献[5]在文献[4]的基础上提出一种启发式的信道分配算法，将信道增益较大的蜂窝用户与受到蜂窝用户干扰较大的D2D多播簇相匹配，大大降低了算法复杂度。为进一步提高频谱利用率，文献[6]提出D2D多播簇和蜂窝用户信道一对多映射的改进信道分配算法。

另一方面，D2D多播系统为保证所有用户的通信质量，簇头根据接收用户中最差信道质量选择发送速率，导致D2D多播容量受限于簇内信道质量最差的用户^[7-8]。为突破D2D多播簇信道容量瓶颈，文献[9]通过禁止多播簇中SINR小于设定门限的用户通信，解决信道质量差的用户对多播簇信道容量的影响，但降低了D2D多播簇用户的公平性。为在保证用户公平性前提下解决多播容量受限问题，传统多播中的经典问题是在总功率约束下最大化最小用户信噪比^[10]。文献[11]最早对该问题进行深入研究，证明该问题是一个非确定性多项式难题(non-deterministic polynomial hard，NP-hard)，并提出一种基于半正定松弛(semi-definite programming，SDR)的算法，缺点是复杂度较高。文献[12-13]分别从加权和信噪比最大化的角度以及在两用户的多播场景下对基于最大化所有用户最小接收信噪比准则的多播通信的波束成形问题进行研究。

本文在支持D2D多播的蜂窝网络中研究以最大化系统总吞吐量为目标的多个D2D用户的分簇策略与资源分配的联合优化问题。文献[4-6]采用简单的基于用户距离的分簇算法，没有考虑无线信道的衰落特性对无线传输的影响。文献[14-15]分别从最小化总传输时延和最大化系统能效的角度研究D2D多播分簇策略，但没有考虑D2D多播簇的信道容量受限于簇内信道质量最差的用户的问题。此外，为解决同频复用干扰，需要对分簇策略和资源分配进行联合优化。因此，本文提出一种新的分簇策略与资源分配的联合优化算法，在保证所有蜂窝用户和D2D用户最小SINR要求的前提下，最大化系统总容量。由于所提优化问题难以获得最优解, 本文通过将该问题分解成功率控制子问题和用户分簇与信道分配两个子问题求得其次优解。即该算法在通过功率控制找到能够复用信道的D2D多播簇与CU的备选集合的基础上，首先采用基于用户信道质量的D2D多播分簇策略(CQCA)进行D2D用户分簇，该分簇策略针对D2D多播信道容量受限于簇内信道质量最差用户的问题，采用改进的k-medoids算法，将用户的信道质量作为聚类算法代价函数中的衡量指标，通过最大化加权最小用户信噪比，实现在保证用户公平性的前提下提升瓶颈用户吞吐量，从而提高D2D多播容量；然后通过联合分簇策略和信道分配，从备选集合中找到最优的信道分配策略，从而减小D2D通信对蜂窝用户产生的同频干扰，以提高蜂窝用户容量。

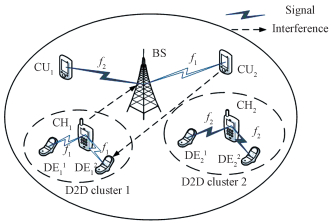
1 系统模型

如图 1所示，单小区满载蜂窝系统中有M个蜂窝用户(Cellular UE，CU)和N个D2D用户。D2D用户形成K(K < M)个D2D多播簇复用CU信道进行文件分发，假设所有D2D用户请求相同的文件。为减小同频干扰，规定每个D2D多播簇最多只能复用1个蜂窝信道，且每个蜂窝信道只能被1个D2D多播簇复用。假设基站能够得到所有蜂窝通信链路和D2D链路的信道状态信息。

假设D2D多播簇k复用蜂窝用户m的信道资源，该D2D多播簇中接收用户d的信道质量可以表示为

$ \beta _{k,m,d}^{{\rm{D2D}}} = \frac{{g_{k,d}^{{\rm{D2D}}}}}{{\sigma _N^2 + P_m^{\rm{C}}g_{k,m,d}^{{\rm{C2D}}}}}, $

(1)

式中：P_m^C为第m个蜂窝用户发射功率；σ_N²为每个信道的加性高斯白噪声功率；g_{k, d}^D2D和g_{k, m, d}^C2D分别表示D2D链路的信道增益和蜂窝用户对D2D干扰链路的信道增益，可以统一表示为

$ {g_{i,j}} = {\zeta _{i,j}} \cdot {\xi _{i,j}} \cdot l_{i,j}^{ - \alpha }, $

(2)

式中：ζ_{i, j}为服从对数正态分布的阴影衰落；ξ_{i, j}为服从瑞利分布的多径衰落；α为路径损耗因子；l_{i, j}为用户之间的距离。

2 问题描述与求解 2.1 问题描述

为在保证所有CU和D2D用户最小SINR的前提下最大化系统总吞吐量，支持D2D多播的蜂窝网络中的关键问题是如何通过合理的分簇策略和资源分配，解决D2D多播信道容量受限于簇内信道质量最差用户的问题，以提升D2D多播簇容量和减小由于D2D多播与CU信道复用产生的同频干扰，从而达到提升CU容量的目的。解决多播容量受限于信道质量最差用户的经典问题是最大化最小用户信噪比，文献[10]进一步证明多播组之间没有同频干扰时最大化最小用户信噪比实际上就等同于最大化多播系统的可达速率。因此，本文建立在保证D2D用户和CU最小SINR前提下，最大化D2D用户和CU和速率的优化问题。

用二进制变量x_{k, m}表示信道复用情况，x_{k, m}=1表示D2D多播簇k复用信道m，否则x_{k, m}=0；用二进制变量ρ_{n, k}=1表示D2D用户n为第k个簇的接收用户，且第k个多播簇的接收用户集合表示为D_k。根据香农公式，第k个多播簇复用蜂窝用户m信道时的吞吐量可以表示为

$ r_{k,m}^{{\rm{D2D}}} = \left| {{D_k}} \right|{B_0}{\log _2}\left( {1 + P_k^{{\rm{D2D}}}\beta _{k,m}^{{\rm{D2D}}}} \right), $

(3)

式中：B₀为信道带宽；β_{k, m}^D2D=$\mathop {{\rm{min}}}\limits_{d \in {D_k}} $β_{k, m, d}^D2D和P_k^D2D分别表示第k个多播簇的信道质量和簇头发射功率。用g_m^C和g_{k, m}^D2C分别表示蜂窝用户m到基站的链路信道增益和第k个多播簇对CU干扰链路的信道增益，则蜂窝用户m的信道质量和吞吐量分别为：

$ \beta _m^{\rm{C}} = \frac{{g_m^{\rm{C}}}}{{\sigma _N^2 + \sum\limits_{k = 1}^K {{x_{k,m}}P_k^{{\rm{D2D}}}g_{k,m}^{{\rm{D2C}}}} }}, $

(4)

$ r_m^{\rm{C}} = {B_0}{\log _2}\left( {1 + P_m^{\rm{C}}\beta _m^{\rm{C}}} \right). $

(5)

支持D2D多播的蜂窝网络的优化问题(P1)建立如下：

$ \begin{array}{l} {\rm{P1}}:\mathop {\max }\limits_{{\rho _n},{k^x}k,m,P_k^{{\rm{D2D}}},P_m^{\rm{C}}} \sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {\sum\limits_{m = 1}^M {{x_{k,m}}{\rho _{n,k}}r_{k,m}^{{\rm{D2D}}}} } } + \sum\limits_{m = 1}^M {r_m^C} ,\\ {\rm{s}}.{\rm{t}}.\;\;\left( {\rm{a}} \right)\gamma _{k,m}^{{\rm{D2D}}} \ge \gamma _{\min }^{D2D},\forall k \in \mathscr{K}\gamma _m^C \ge \gamma _{\min }^C,\forall m \in \mathscr{M},\\ \left( {\rm{b}} \right)\sum\limits_{m = 1}^M {{x_{k,m}}} \le 1,\forall k \in \mathscr{K}\sum\limits_{k = 1}^M {{x_{k,m}}} \le 1,\forall m \in \mathscr{M},\\ \left( {\rm{c}} \right)\sum\limits_{n = 1}^N {{\rho _{n,k}}} \le \left| {{D_k}} \right|,\forall k \in \mathscr{K}\sum\limits_{k = 1}^K {{\rho _{n,k}}} = 1,\forall n \in \mathscr{N},\\ \left( {\rm{d}} \right){\rho _{n,k}} \in \left\{ {0,1} \right\},{x_{k,m}} \in \left\{ {0,1} \right\},\forall k \in \mathscr{K},\forall n \in \mathscr{N},\\ \left( {\rm{e}} \right)0 \le P_k^{{\rm{D2D}}} \le P_{\max }^{{\rm{D2D}}},0 \le P_m^{\rm{C}} \le P_{\max }^{\rm{C}},\forall k \in \mathscr{K}. \end{array} $

(6)

其中，约束(a)为D2D用户和CU的最小SINR约束；约束(b)为信道资源约束，即任意一个D2D多播簇只能复用一个CU信道；约束(c)为D2D多播成簇关系，即D2D用户仅属于唯一多播簇，且|D_k|等于第k多播簇的接收用户数；约束(d)为配对关系约束，即|D_k|个D2D用户仅与一个CU用户配对；约束(e)是D2D多播簇和CU的最大功率约束。

2.2 问题求解

优化问题P1是典型的混合整数非线性规划问题，且存在用户分簇和资源分配的耦合问题，导致该优化问题随着系统中用户数目的增加会变得极其复杂。由于系统总吞吐量由多个CU吞吐量和与其信道复用的D2D多播簇吞吐量构成，因此该系统总吞吐量需要考虑两个问题：1)单个D2D多播簇和CU复用信道资源时，如何进行功率控制最大化其和速率；2)如何进行D2D用户分簇以及D2D多播簇和CU的信道分配以最大化系统总吞吐量。因此本文考虑将优化问题划分为两个子问题求解：功率控制子问题和用户分簇与信道分配子问题。通过子问题1)给出满足QoS要求的D2D多播簇和CU用户的最优功率分配方案；通过子问题2)可以实现D2D用户分簇，并为D2D多播簇从子问题1)中的CU集合中找到最优的CU复用组合，即联合信道分配来最大化总吞吐量。

2.2.1 功率控制

为确定在满足CU和D2D用户最小SINR的前提下D2D多播簇k是否可以与蜂窝用户m复用信道，并求解出满足功率约束的最优功率分配对以实现D2D多播簇k与蜂窝用户m和速率的最大化，本文首先考虑问题P1的约束(a)和(e)，建立功率控制子问题P2：

$ \begin{array}{l} {\rm{P2}}:\mathop {\max }\limits_{P_k^{{\rm{D2D}}},P_m^{\rm{C}}} \left( {r_k^{{\rm{D2D}}} + r_m^{\rm{C}}} \right),\\ {\rm{s}}.{\rm{t}}.\;\;\left( {\rm{a}} \right)\gamma _m^{\rm{C}} \ge \gamma _{\min }^{\rm{C}},\forall m \in \mathscr{M},\\ \left( {\rm{b}} \right)\gamma _{k,m}^{{\rm{D2D}}} \ge \gamma _{\min }^{{\rm{D2D}}},\forall k \in \mathscr{K},\\ \left( {\rm{c}} \right)0 \le P_k^{{\rm{D2D}}} \le P_{\max }^{{\rm{D2D}}},0 \le P_m^{\rm{C}} \le P_{\max }^{\rm{C}},\forall k \in \mathscr{K}. \end{array} $

(7)

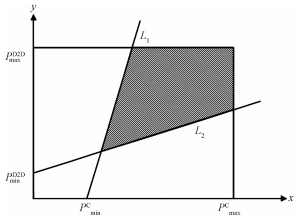
P2的约束条件(a)表征CU和D2D多播簇占用相同信道资源的情况下最小信干噪比与发射功率间的关系，因此该问题可以通过几何规划求解，并求出D2D多播簇k与蜂窝用户m复用信道时最优的功率分配对。如图 2所示，x，y轴表示CU和D2D多播簇用户的发射功率，直线L₁和L₂分别表示P2的约束条件(a)、(b)，该问题有可行解的充要条件是直线L₁斜率必须大于直线L₂斜率，且交点属于P_max^D2D和P_max^C构成的矩形可行域内。即满足：

$ \begin{array}{l} \frac{{P_{\min }^{\rm{C}}g_{k,m}^{{\rm{D2D}}}}}{{g_m^{\rm{C}}}} > \frac{{P_{\min }^{{\rm{D2D}}}g_{k,{d_{\min }}}^{{\rm{C2D}}}}}{{g_{k,{d_{\min }}}^{{\rm{D2D}}}}},\\ 0 \le P_{{\rm{D2D}}}^ * \le P_{\max }^{{\rm{D2D}}},\\ 0 \le P_{\rm{C}}^ * \le P_{\max }^{\rm{C}}. \end{array} $

(8)

公式(8)可作为判定D2D多播簇和CU是否能够进行信道复用的重要条件。其中，$P_{{\rm{min}}}^{\rm{C}} = \frac{{\sigma _N^2\gamma _{{\rm{min}}}^{\rm{C}}}}{{g_m^{\rm{C}}}}$，$P_{{\rm{min}}}^{{\rm{D2D}}} = \frac{{\sigma _N^2\gamma _{{\rm{min}}}^{{\rm{D2D}}}}}{{{g}_{k,{d_{{\rm{min}}}}}^{{\rm{D2D}}}}}$，$P_{{\rm{D2D}}}^* = \frac{{\left( {g_{k, {d_{{\rm{min}}}}}^{{\rm{C2D}}}P_{{\rm{min}}}^{\rm{C}}P_{{\rm{min}}}^{{\rm{D2D}}} + g_m^{\rm{C}}P_{{\rm{min}}}^{{\rm{D2D}}}} \right)\sigma _N^2}}{{g_{k, {\mathit{d}_{{\rm{min}}}}}^{{\rm{D2D}}}g_m^{\rm{C}}-P_{{\rm{min}}}^{\rm{C}}P_{{\rm{min}}}^{{\rm{D2D}}}g_{k, {d_{{\rm{min}}}}}^{{\rm{C2D}}}g_m^{\rm{C}}}}$，$P_{\rm{C}}^* = \frac{{\left( {g_{k, {d_{{\rm{min}}}}}^{{\rm{D2D}}}P_{{\rm{min}}}^{\rm{C}} + g_m^{\rm{C}}P_{{\rm{min}}}^{\rm{C}}P_{{\rm{min}}}^{{\rm{D2D}}}} \right)\sigma _N^2}}{{g_{k, {\mathit{d}_{{\rm{min}}}}}^{{\rm{D2D}}}g_m^{\rm{C}}-P_{{\rm{min}}}^{\rm{C}}P_{{\rm{min}}}^{{\rm{D2D}}}g_{k, {d_{{\rm{min}}}}}^{{\rm{C2D}}}g_m^{\rm{C}}}}$，g_{k, dmin}^D2D对应于满足β_{k, m}^D2D=$\mathop {{\rm{min}}}\limits_{d \in {D_k}} \beta _{k, m, d}^{{\rm{D2D}}}$的D2D用户的信道增益。并根据文献[16]的引理3可知，最优功率分配对(P_D2D^max, P_C^max)仅可能出现在图 2阴影区域的边界上。

2.2.2 用户分簇与信道分配

在求得D2D多播簇可以复用信道资源的备选CU用户集合及其最优功率分配对(P_D2D^max, P_C^max)的基础上，需要联合D2D用户分簇和信道分配，为每一个D2D多播簇从P2中的备选集合中找到最优的CU复用搭档，此时，子问题P3为如下形式：

$ \begin{array}{l} {\rm{P3}}:\mathop {\max }\limits_{{\rho _{n,k}}{x_{k,m}}} \left( {\sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {\sum\limits_{m = 1}^M {{x_{k,m}}{\rho _{n,k}}r_k^{{\rm{D2D}}}} } } + \sum\limits_{m = 1}^M {r_m^C} } \right),\\ {\rm{s}}.{\rm{t}}.\left( {\rm{a}} \right)\sum\limits_{m = 1}^M {{x_{k,m}}} \le 1,\forall k \in \mathscr{K}\sum\limits_{k = 1}^M {{x_{k,m}}} \le 1,\forall m \in \mathscr{M},\\ \left( {\rm{b}} \right)\sum\limits_{n = 1}^N {{\rho _{n,k}}} \le \left| {{D_k}} \right|,\forall k \in \mathscr{K}\sum\limits_{k = 1}^K {{\rho _{n,k}}} = 1,\forall n \in \mathscr{N},\\ \left( {\rm{c}} \right){\rho _{n,k}} \in \left\{ {0,1} \right\},{x_{k,m}} \in \left\{ {0,1} \right\},\forall k \in \mathscr{K},\forall n \in \mathscr{N}. \end{array} $

(9)

该优化目标由D2D多播簇容量和CU容量共同组成，其中D2D多播簇容量受分簇策略和CU对D2D用户的同频干扰的共同影响，CU容量仅受D2D多播簇头对CU的同频干扰影响。因此可先通过分簇策略优化D2D多播簇容量，该多播簇容量的表达式与k-medoids聚类算法的代价函数具有相同的结构，因此可以用k-medoids算法求解。再通过计算CU的代价函数进行信道分配，降低簇头对CU的同频干扰，从而提升CU容量。

首先通过分簇策略优化D2D多播簇容量。由文献[10]可知，多播组之间没有同频干扰时，最大化多播系统的可达速率等价于最大化最小用户信噪比，因此问题P3的优化目标第一项可等价为

$ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{{\rho _{n,k}}{x_{k,m}}} \sum\limits_{k = 1}^K {\sum\limits_{n = 1}^N {\left( {\left| {{D_k}} \right| \cdot \mathop {\min }\limits_{1 \le d \le \left| {{D_k}} \right|} \frac{{g_{k,d}^{{\rm{D2D}}}}}{{\sigma _N^2 + \sum\limits_{m = 1}^M {{x_{k,m}}P_m^{\rm{C}}g_{k,m,d}^{{\rm{C2D}}}} }}} \right)} } }\\ { = \mathop {\max }\limits_{{\rho _{n,k}}{x_{k,m}}} \sum\limits_{k = 1}^K {\sum\limits_{n = 1}^N {\left( {\left| {{D_k}} \right| \cdot \mathop {\min }\limits_{1 \le d \le \left| {{D_k}} \right|} \beta _{k,d}^{{\rm{D2D}}}} \right)} } .} \end{array} $

(10)

该优化目标与k-medoids聚类算法的代价函数具有相同的结构，因此可以用k-medoids算法求解。K-medoids算法的聚类过程是通过交替优化聚类中心和分到已知聚类中心的数据点，最小化每个类中数据点到其聚类中心的距离平方和，即实现$\mathop {{\rm{min}}}\limits_{{\rho _{n, k}}} \sum\limits_{k = 1}^K {{{\sum\limits_{n = 1}^N {{\rm{min}}\;\left| {{x_n}-{a_k}} \right|} }^2}} $，从而将数据点划分为k个类。由于k-medoids算法复杂度为O(N²)。当N较大时，复杂度比较高，因此在采用k-medoids算法分簇前先通过基于密度聚类的DBSCAN^[17]进行簇头筛选，达到降低算法复杂度的目的。

其次，通过信道分配降低簇头对CU的同频干扰，从而提升CU容量。针对P3问题中优化目标中的第2项，本文通过计算每次分簇结果下不同信道分配情况的CU代价函数Q₂=P_m^Cβ_m^C来保证CU容量。如果CU代价函数均不满足设定值，则重新分簇；否则从所有的信道分配情况中选取Q₂值最大的信道分配结果。在计算算法复杂度时，设外循环的循环次数为T，求解P2问题的复杂度为第k个D2D多播簇中D2D用户个数|D_k|的函数，即P2问题复杂度为f(|D_k|)^[5]，则所提算法复杂度为O(TN²+TM·$\sum\limits_{k = 1}^K f $(|D_k|))，由于所提算法在步骤1中采用基于密度聚类的DBSCAN^[17]算法进行簇头选取，使得外循环的迭代次数T可设定合适参数，以保证复杂度控制在合理范围内。

表 1给出基于功率控制的D2D多播分簇与信道分配的联合优化策略算法流程。

3 仿真结果与分析 3.1 仿真参数

考虑单小区网络，基站位于小区中心，CU和D2D用户均匀分布在小区内，小区半径为300 m。系统带宽为10 MHz，假设系统带宽平均分配给所有蜂窝用户，仿真参数如表 2所示。

3.2 仿真结果与分析

为验证所提基于用户信道质量分簇算法(CQCA)的仿真性能，考虑如下算法进行对比：基于随机分簇的基准对比算法(random-based clustering algorithm，RCA)；基于用户距离分簇算法^[5](distance-based clustering algorithm，DCA)和基于QoS保证准则的分簇算法^[9](qos guarantee-based clustering algorithm，QCA)。

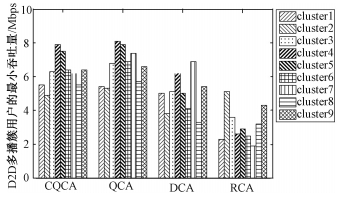
图 3为各分簇算法的D2D多播簇中最小吞吐量用户的吞吐量示意图。其中，D2D多播簇数目K为9。仿真表明，相较于RCA、DCA分簇算法，所提的CQCA算法针对簇内最差信道质量的用户这一瓶颈做出良好改善，明显提高了限制D2D多播簇容量的用户吞吐量。原因是CQCA算法以最大化每个簇中最差信道质量作为聚类算法的代价函数，提升信道质量最差D2D用户的信道容量。CQCA性能略差于QCA性能，是因为QCA针对D2D簇内最差用户进行了静默，使得信道最差的用户不会对簇内其他用户造成影响，但降低了用户间的公平性。

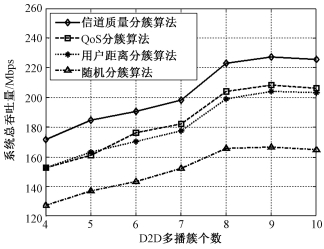
图 4为各分簇算法的D2D多播簇个数对系统总吞吐量的影响。所有分簇算法的系统总吞吐量先随D2D多播簇个数的增大而增加，原因是，随着D2D多播簇中用户数目不断减少，多播组内用户间信道质量的差异逐渐减小，簇内信道质量最差用户的吞吐量经优化逐渐增大，这与传统多播中通过划分组播改善容量受限问题的结论是一致的；当D2D多播簇个数大于9时，系统总吞吐量不再增加并且略有下降，原因是，D2D多播簇数目持续增大，导致D2D多播簇簇头对CU的干扰亦增加。最佳分簇数K的选取可通过检验聚类有效性指标或构造代价函数的方式确定，根据现有文献[18]，K=8的“拐点”处是效率最高的分簇数，但K=9是代价函数公式(9)最大的值，因此本文为实现系统总吞吐量最大化而选取K=9作为该场景的最优分簇数。仿真表明，所提算法相比于DCA和RCA性能提升12%和35%。

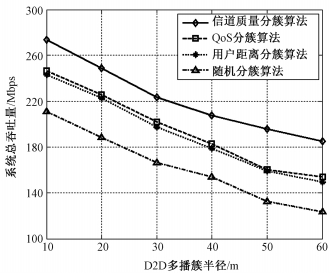
图 5为D2D多播簇最大通信半径对系统总吞吐量的影响。仿真表明，不同算法下系统总吞吐量均随着D2D多播簇最大通信半径的增大而减小，原因是随着D2D通信半径增加，D2D信道增益减小，为保证D2D用户的QoS，D2D簇头的发射功率增大，导致对CU的同频干扰增大，因此系统总吞吐量下降。此外，所提算法相较于对比算法系统总吞吐量随着D2D最大通信半径的增加而减小的速率更缓慢，原因是，所提算法直接针对用户信道质量进行优化，对用户间距离的敏感度较低，表现出对距离的稳健性。

4 结束语

在支持D2D多播的蜂窝网络中，本文研究D2D用户复用蜂窝信道进行D2D多播文件分发时的分簇策略与资源分配的联合优化问题。针对该场景下D2D多播信道容量受限于簇内信道质量最差用户的问题和信道复用产生的同频干扰，提出一种基于k-medoids的用户信道分簇策略(CQCA)与资源分配的联合优化算法，在保证所有蜂窝用户和D2D用户最小SINR要求的前提下，最大化系统总容量。仿真表明，所提CQCA算法相比于传统分簇策略能够显著提升多播簇瓶颈用户吞吐量，从而提高多播簇容量和系统总吞吐量。并通过仿真给出该场景下参考分簇数目。