星载SAR是一种能够实现全天时、全天候对地高分辨观测的微波遥感系统，自美国1978年成功发射Seasat-1 SAR卫星以来，许多国家都发射了SAR卫星，星载SAR在国土测量、海洋水文观测、环境灾害监测以及军事侦察等领域都发挥了重要的作用^[1]。

与传统的星载SAR获取微波遥感静态图像相比，星载视频SAR有效扩展了时间维的信息，能够对热点区域进行持续监测，这使得SAR系统具有更强的动态信息获取能力，星载视频SAR将SAR成像技术与视频显示技术相结合，经过后续处理能够得到热点区域的SAR视频产品，从而直观反映出运动目标的位置、速度及运动趋势等运动参数信息^[2]。

近年来对视频SAR的研究主要集中在机载平台：文献[3]提出圆迹飞行的机载视频SAR系统，并研究视频SAR的自聚焦算法用来解决圆迹飞行过程中场景旋转的问题；文献[4]对机载平台中振动误差对视频SAR成像质量的影响进行分析，并给出补偿方法；文献[5]首次公开提出星载视频SAR的概念，并分析帧频与数据重叠率的关系，给出一种改进的DCS视频SAR的成像算法；文献[6]提出条带式视频SAR的参数推导方法，并进行仿真分析。目前国内外基于星载平台的视频SAR研究尚处于起步阶段，且公开文献中主要对视频SAR成像算法进行研究，尚无对星载视频SAR实现方法的研究。

星载视频SAR相对于机载视频SAR而言具有观测幅宽大、不受地域限制的优点，但单个低轨卫星对固定区域的有效观测时间相对有限，低轨星载视频SAR可通过多星组网有效延长观测时间，对于高轨SAR而言，随着地球同步轨道SAR卫星的逐步发展，通过合理的轨道设计以及波束指向控制可以实现对固定区域的长时间凝视视频观测，本文主要论述低轨卫星实现视频SAR成像的姿态机动策略。

敏捷SAR卫星天线固定在卫星上，通过整星姿态机动实现波束扫描，本文基于精确的轨道与地球模型，利用敏捷SAR卫星姿态机动实现对固定场景的持续视频监测，同时为有效增大观测区域面积并获得稳定的视频图像，通过偏航补偿的方法实现观测场景的图像的无旋转控制。文中提出的敏捷卫星视频成像模式姿态控制策略可为敏捷SAR卫星新的应用模式提供实现基础。

1 星载视频SAR成像模式

星载视频SAR模式主要实现对固定场景的持续监测，实现对时变场景或运动目标的观测，所以需要尽可能延长固定场景的观测时间。对地球同步卫星而言，可以利用合理的轨道参数设计实现对固定场景的持续观测；而对于低轨卫星而言，星载视频SAR一般工作在大角度聚束模式下，工作期间天线波束中心始终指向场景中心。传统的聚束模式通过延长方位向的合成孔径时间实现高分辨成像，而视频SAR通过对大角度聚束模式下回波数据的合理分割形成该场景的序贯图像序列，经过图像处理后以视频的形式再现目标场景的信息。

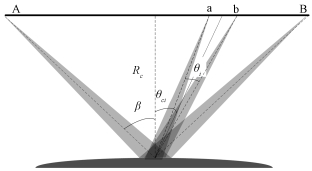
等效斜视模式下低轨卫星工作示意图如图 1所示，AB段为低轨卫星聚束模式下的数据录取长度，ab为第i个视频帧的数据录取长度，R_c为最近斜距，2β为聚束模式下的最大合成孔径角，θ_i为第i个视频帧的合成孔径角，θ_ci为第i个视频帧的斜视角。则第i个视频帧的多普勒带宽为

$ {B_{{\rm{a}}\left( i \right)}} = {f_{{\rm{d}}\left( b \right)}} - {f_{{\rm{d}}\left( a \right)}}. $

(1)

卫星位于位置b时多普勒频率为${f_{{\rm{d}}\left(b \right)}} = 2{V_{\rm{r}}}{\rm{sin}}\left({{\theta _{{\rm{c}}\mathit{i}}} + \frac{{{\theta _i}}}{2}} \right)/\lambda $，位于位置a时多普勒频率为${f_{{\rm{d}}\left(a \right)}} = 2{V_{\rm{r}}}{\rm{sin}}\left({{\theta _{{\rm{c}}\mathit{i}}} + \frac{{{\theta _i}}}{2}} \right)/\lambda $，其中V_r为卫星平台的运动速度，λ为载波波长，由此可得第i个视频帧的多普勒带宽为

$ {B_{{\rm{a}}\left( i \right)}} = \frac{{4{V_{\rm{r}}}\cos {\theta _{{\rm{c}}i}}\sin \frac{{{\theta _i}}}{2}}}{\lambda } \approx \frac{{2{V_{\rm{r}}}{\theta _i}\cos {\theta _{{\rm{c}}i}}}}{\lambda }. $

(2)

所以星载视频SAR一帧图像方位向的分辨率为：${\rho _{{\rm{a}}\mathit{i}}} = \frac{{{V_{\rm{r}}}}}{{{B_{{\rm{a}}\left(i \right)}}}} = \lambda \frac{{{V_{\rm{r}}}}}{{2{V_{\rm{r}}}}}\frac{1}{{{\theta _i}}}\frac{1}{{{\rm{cos}}{\theta _{{\rm{c}}\mathit{i}}}}}$，若第i个视频帧的数据中心时刻为t_i，则在给定方位向分辨率的前提下，第i个视频帧的数据录取长度为L_i=$\frac{{{\theta _i}{R_{\rm{c}}}}}{{{\rm{co}}{{\rm{s}}^2}{\theta _{{\rm{c}}\mathit{i}}}}}$，整理可得第i个视频帧的数据长度为

$ {L_i} = \frac{{\lambda {V_{\rm{r}}}{R_{\rm{c}}}}}{{2{V_{\rm{r}}}{\rho _{{\rm{a}}i}}{{\cos }^3}{\theta _{{\rm{c}}i}}}} = \frac{{\lambda {{\left( {R_{\rm{c}}^2 + V_{\rm{r}}^2t_i^2} \right)}^{3/2}}}}{{2{\rho _{{\rm{a}}i}}R_{\rm{c}}^2}}. $

(3)

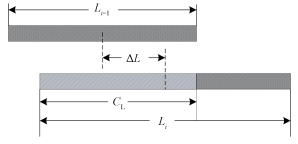
由于在天基视频SAR成像中，帧周期小于合成孔径时间，所以相邻帧之间的回波数据就不可避免地要有重叠^[7-8]。假设相邻两帧之间的时间间隔(即帧周期)为T_f，则相邻两帧之间的重叠关系示意图如图 2所示。

图 2中L_i为第i个视频帧的长度，ΔL为相邻两个视频帧间隔距离，C_L为重叠的长度，则重叠长度为

$ {C_{\rm{L}}} = \frac{{{L_i}}}{2} + \left( {\frac{{{L_{i - 1}}}}{2} - \Delta L} \right) = \frac{{{L_i} + {L_{i - 1}}}}{2} - {T_{\rm{f}}}{V_{\rm{r}}}. $

(4)

由此可得第i个视频帧的重叠率为${\alpha _i} = \frac{{{C_{\rm{L}}}}}{{{L_i}}}$，整理得重叠率为

$ {\alpha _i} = \frac{1}{2} + \frac{{\lambda {{\left( {R_{\rm{c}}^2 + V_{\rm{r}}^2{{\left( {{t_i} - {T_{\rm{f}}}} \right)}^2}} \right)}^{3/2}} - 4{T_{\rm{f}}}{V_{\rm{r}}}R_{\rm{c}}^2{\rho _{{\rm{a}}i}}}}{{2\lambda {{\left( {R_{\rm{c}}^2 + V_{\rm{r}}^{\rm{2}}t_i^2} \right)}^{3/2}}}}. $

(5)

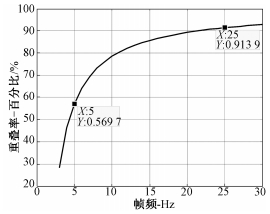
假设卫星轨道高度为567 km，载波频率为9.6 GHz，下视角为30°，方位向分辨率为3 m，帧频与重叠率的关系曲线如图 3所示，可以看出，若帧频为5 Hz，则重叠率为57%，如果帧频为25 Hz，则重叠率将达到91.4%。

2 视频成像模式姿态机动策略 2.1 坐标系定义

地球惯性系(O-x_iy_iz_i)、地球固连系(O-x_ey_ez_e)、轨道坐标系(O_s-x_oy_oz_o)、卫星本体系(O_s-x_by_bz_b)的定义见文献[9]，假设姿态角为0°时，卫星本体坐标系与轨道坐标系重合，同时假设卫星天线固连在星本体上，波束指向与卫星本体坐标系的Z轴重合。

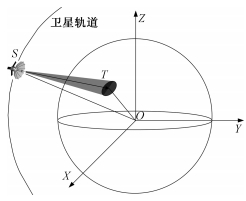
2.2 目标场景中心凝视

为了在卫星与目标场景中心有相对运动的情况下实现对场景中心凝视跟踪，需要通过卫星整星姿态机动实现波束指向对观测矢量的跟踪^[10-11]，场景中心凝视几何模型如图 4所示。

轨道坐标系下卫星位于S处时位置矢量为r_s^o=[0 0 0]^T，场景中心T在地球固连系下的位置矢量为(λ δ h_T)，其中λ为场景中心点的经度，δ为场景中心点的纬度，h_T为场景中心点的高程，地面目标点应选择在考虑卫星滚转向机动能力下的可观测范围内，则场景中心点在地球惯性系下的位置矢量^[9]为

$ \mathit{\boldsymbol{r}}_{\rm{T}}^i = \left| {\mathit{\boldsymbol{r}}_{\rm{T}}^i} \right|\left[ \begin{array}{l} \cos \beta \cos \alpha \\ \cos \beta \sin \alpha \\ \sin \beta \end{array} \right]. $

(6)

式中:|r_Tⁱ|=$\frac{{{a_e} \times {b_e}}}{{\sqrt {a_e^2 \times {\rm{si}}{{\rm{n}}^2}\beta + b_e^2 \times {\rm{co}}{{\rm{s}}^2}\beta } }} + {h_{\rm{T}}}$，a_e为地球长半轴，b_e为地球短半轴；α、β场景中心的地心经度与地心纬度，表达式为

$ \left\{ \begin{array}{l} \alpha = \lambda + {\mathit{\Omega }_G}\\ \beta = \arctan \left[ {\left( {^1 - {f_0}} \right)2\tan \delta } \right] \end{array} \right.. $

(7)

式中：Ω_G=Ω_G0+ω_e(t-t₀)为t时刻的格林尼治恒星时角, f₀为地球扁率。场景中心点在轨道坐标系下的位置矢量为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{r}}_{\rm{T}}^o = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&{ - 1}\\ { - 1}&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos u}&{\sin u}&0\\ { - \sin u}&{\cos u}&0\\ 0&0&1 \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos i}&{\sin i}\\ 0&{ - \sin i}&{\cos i} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \mathit{\Omega }}&{\sin \mathit{\Omega }}&0\\ { - \sin \mathit{\Omega }}&{\cos \mathit{\Omega }}&0\\ 0&0&1 \end{array}} \right]}\\ {\mathit{\boldsymbol{r}}_{\rm{T}}^i + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{R_e} + h} \end{array}} \right].} \end{array} $

(8)

式中：升交点幅角u=ω+f，其中ω为近地点幅角，即近地点到升交点的角距，f为真近点角，即卫星相对于近地点的角距；i为轨道倾角；Ω为升交点赤经。由此可得轨道坐标系观测矢量为r_ST^o=r_T^o。

若天线与星体固连且波束指向与本体坐标系的Z轴重合，但天线相位中心与卫星质心并不重合，则天线指向在本体坐标系下的矢量为r_A^b=[0 0 L_c]^T，则按照1-2-3转序，天线波束指向在质心轨道坐标系下的矢量为

$ \mathit{\boldsymbol{r}}_{\rm{A}}^o = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{ - \cos \theta \sin \psi }&{\sin \theta }\\ {\sin \varphi \sin \theta \cos \psi + \cos \varphi \sin \psi }&{ - \sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi }&{ - \sin \varphi \cos \theta }\\ { - \cos \varphi \cos \psi \sin \theta + \sin \varphi \sin \psi }&{\cos \varphi sin\theta sin\psi + sin\varphi cos\psi }&{\cos \varphi \cos \theta } \end{array}} \right]\mathit{\boldsymbol{r}}_{\rm{A}}^b. $

(9)

式中：θ，ψ，$φ$分别为俯仰角、偏航角和滚转角。要实现对场景中心点的跟踪，则需要质心轨道坐标系下天线的波束指向r_A^o实时跟踪观测矢量r_ST^o，则有如下矢量关系成立

$ \left[ {\begin{array}{*{20}{c}} {x_{{\rm{ST}}}^o}\\ {y_{{\rm{ST}}}^o}\\ {z_{{\rm{ST}}}^o} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{ - \cos \theta \sin \psi }&{\sin \theta }\\ {\sin \varphi \sin \theta \cos \psi + \cos \varphi \sin \psi }&{ - \sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi }&{ - \sin \varphi \cos \theta }\\ { - \cos \varphi \cos \psi \sin \theta + \sin \varphi \sin \psi }&{\cos \varphi sin\theta sin\psi + sin\varphi cos\psi }&{\cos \varphi \cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]. $

(10)

式中：[x_ST^o y_ST^o z_ST^o]^T为r_ST^o的单位矢量的三轴分量，则由此可得俯仰与滚转角的姿态需求为

$ \left\{ \begin{array}{l} \varphi = - \arctan \left( {\frac{{y_{{\rm{ST}}}^o}}{{z_{{\rm{ST}}}^o}}} \right)\\ \theta = \arcsin \left( {x_{{\rm{ST}}}^o} \right) \end{array} \right.. $

(11)

至此通过滚转与俯仰向的姿态控制实现对场景中心点的凝视观测。

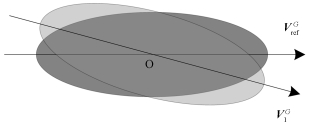
2.3 波束覆盖区域无旋转控制

通过滚转与俯仰向的控制可以实现对场景中心点O凝视观测，如果不进行偏航控制则波束覆盖区域将会发生旋转，示意图如图 5所示，为了获得最大观测范围并获得稳定的视频帧图像，采用敏捷卫星偏航补偿实现波束覆盖区域的无旋转控制。

定义参考时刻t_ref波束覆盖区域在地球固连系下的矢量为V_ref^G，通过坐标变化将其转换到质心轨道坐标系下为V_ref^O，若偏航角为0，则由上节中计算的俯仰与滚转角将V_ref^O转换到卫星本体坐标系为V_ref^b。由于天线的安装矢量不随时间改变，在任意时刻t，要保证波束覆盖区域无旋转，则其矢量仍为V_ref^G，将该参考矢量转换到质心轨道坐标系下为V_t^O，经过偏航控制后转换到卫星本体坐标系后仍为V_ref^b，有如下等式成立

$ \mathit{\boldsymbol{V}}_{{\rm{ref}}}^b = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{\sin \psi }&0\\ { - \sin \psi }&{\cos \psi }&0\\ 0&0&1 \end{array}} \right]\mathit{\boldsymbol{V}}_t^O. $

(12)

式中：ψ即为需要补偿的偏航角，经过偏航补偿后可以实现波束覆盖区域的无旋转控制。

2.4 敏捷SAR卫星姿态运动学方程

基于欧拉1-2-3旋转，通过θ，ψ，$φ$这3个欧拉角将敏捷SAR卫星的空间转动角速度在本体坐标系下的分量ω_x、ω_y、ω_z用欧拉角表示，从而建立敏捷SAR卫星的姿态运动学方程为

$ \left\{ \begin{array}{l} {\omega _x} = \dot \varphi \cos \psi cos\theta + \dot \theta sin\psi \\ {\omega _y} = - \dot \varphi \sin \psi cos\theta + \dot \theta cos\psi \\ {\omega _z} = \dot \psi + \dot \varphi \sin \theta \end{array} \right.. $

(13)

3 视频SAR持续观测星座设计

星载视频SAR能够实现对热点区域的持续监测，但在星载应用中受卫星斜视角与可见范围的约束，单星观测时间较短。为了实现热点区域的连续视频监测，需要通过卫星组网顺序通过目标区域上空，接收目标区域的回波信号，实现持续覆盖。

卫星星座设计采用经典的Walker星座构型，共有N颗卫星，分布在P个轨道面内，各个轨道面的轨道倾角和轨道高度相同，升交点以360°/P均匀分布，每个轨道面内有S颗卫星，按360°/S等间隔均匀分布。

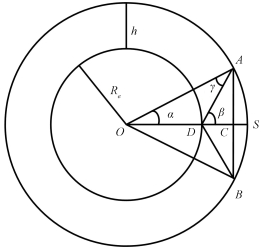
单星覆盖的几何示意图如图 6所示，卫星的有效观测弧段为AB，由几何关系可得

$ \left( {{R_e} + h} \right)\cos \alpha - \frac{{\left( {{R_e} + h} \right)\sin \alpha }}{{\tan \beta }} = {R_e}. $

(14)

由式(14)可得α，则卫星的有效测控时间为

$ {T_v} = \frac{{2\alpha }}{\omega }. $

(15)

式中：$\omega = \sqrt {\frac{\mu }{{{{\left({{R_e} + h} \right)}^3}}}} $为卫星运行的轨道角速度，μ为地球引力常数。

所以一个轨道面内所需的卫星数量为

$ S = \left\lceil {\frac{T}{{{T_v}}}} \right\rceil . $

(16)

式中：$\left\lceil \cdot \right\rceil $为向上取整，$T = 2{\rm{ \mathit{ π} }}\sqrt {\frac{{{{\left({{R_e} + h} \right)}^3}}}{\mu }} $为轨道周期。卫星运行一圈后星下点轨迹在地球赤道上的经度变化为

$ \Delta \varphi = - 2{\rm{ \mathsf{ π} }}\frac{T}{{{T_e}}}, $

(17)

其中T_e为地球自转周期，回归轨道的条件为

$ n \left| {\Delta \varphi } \right| = m2{\rm{ \mathsf{ π} }}. $

(18)

为提高卫星的利用效率，取m=1，则轨道面个数为

$ P = \frac{{2{\rm{ \mathsf{ π} }}}}{{\left| {\Delta \varphi } \right|}}. $

(19)

由此可得实现持续视频监测需要的低轨卫星总数为

$ N = PS. $

(20)

假设轨道高度h=567 km，聚束模式下的最大入射角β=65°，单个轨道面上所需的卫星数量S=12，卫星轨道周期为T=1.6 h，故轨道面的个数为P=15，由此可得实现目标区域的持续监测所需的Walker星座中卫星数量为N=180颗，即通过180颗卫星组成的星座可实现对特定区域的持续覆盖。

4 设计实例与仿真

基于上述分析，文章对美国驻日本佐世保海军基地进行视频成像时的卫星三轴姿态进行仿真分析，仿真参数如下表所示，首先计算多普勒中心频率为0的时刻T₀为2016-11-25 T08:09:43，通过计算可得观测时间为2016-11-25 T08:08:03—2016-11-25 T08:11:23。仿真参数如表 1所示。

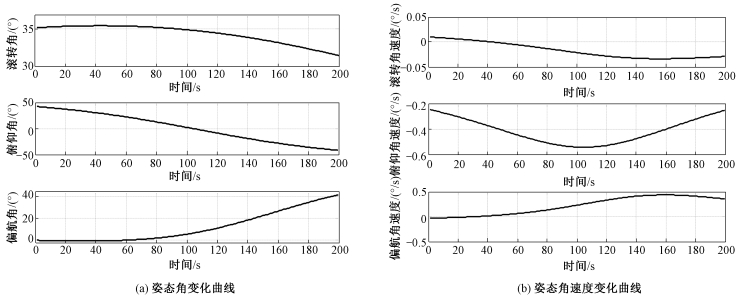
视频成像期间三轴姿态角及姿态角速度的变化曲线如图 7所示。

可以看出视频成像过程中卫星主要依靠卫星俯仰向的大角度姿态机动能力实现凝视观测，滚转向姿态机动角度较小，偏航向的在台机动主要为了实现波束覆盖区域的无旋转控制，卫星姿态机动能力可以满足卫星三轴的姿态角与姿态角速度的需求，卫星姿态机动方案有效可行。

首先通过STK建立仿真场景，然后将计算所得的欧拉角与欧拉角速度导入STK进行仿真分析。图 8为起始时刻、中间时刻与结束时刻波束覆盖区域与目标场景的匹配关系。由图中可以看出，通过偏航控制实现波束覆盖区域的无旋转控制，有效增大观测范围，同时为基于视频SAR的运动目标检测提供稳定的SAR图像序列。

在视频成像的过程中卫星平台的控制误差将导致波束指向精度误差，波束指向精度误差主要会造成波束覆盖区域中心点的移动或者是旋转，其中在卫星姿态指向精度为统计意义下的常值的假设下，卫星俯仰向与滚转向的姿态指向精度误差将导致波束覆盖范围中心点的移动，这种移动只是影响单帧图像的灵敏度、模糊度以及几何分辨率等性能指标，并不会对视频的稳定性造成影响，而当偏航角存在指向精度误差时，将会造成波束覆盖区域的旋转，导致视频稳定性以及两帧视频重叠区域的下降。

5 结论

本文对基于大角度凝视聚束的星载视频SAR成像模式及成像过程中的姿态机动策略进行研究，给出视频SAR回波数据分割的解析表达式，同时实现对观测场景的凝视成像，并利用偏航角补偿实现波束覆盖区域的无旋转控制，有效增大观测场景的范围的同时能够为后续基于SAR视频的运动目标检测以及视频显示提供稳定的图像，通过设计实例的仿真分析表明文章提出的姿态机动策略能够满足敏捷SAR卫星姿态机动能力的约束，方案可行有效，对于星载视频SAR而言成像时间短是制约星载视频SAR发展的主要因素之一，可以通过卫星组网实现对特定场景区域的长时间视频监测，本文的研究工作可为基于敏捷SAR卫星的视频成像模式设计提供设计参考及依据。